解析2021-2022学年高一上学期数学人教A版(2019)必修第一册第二章 一元二次函数、方程和不等式单元检测过关卷(Word含答案解析)
文档属性
| 名称 | 解析2021-2022学年高一上学期数学人教A版(2019)必修第一册第二章 一元二次函数、方程和不等式单元检测过关卷(Word含答案解析) | 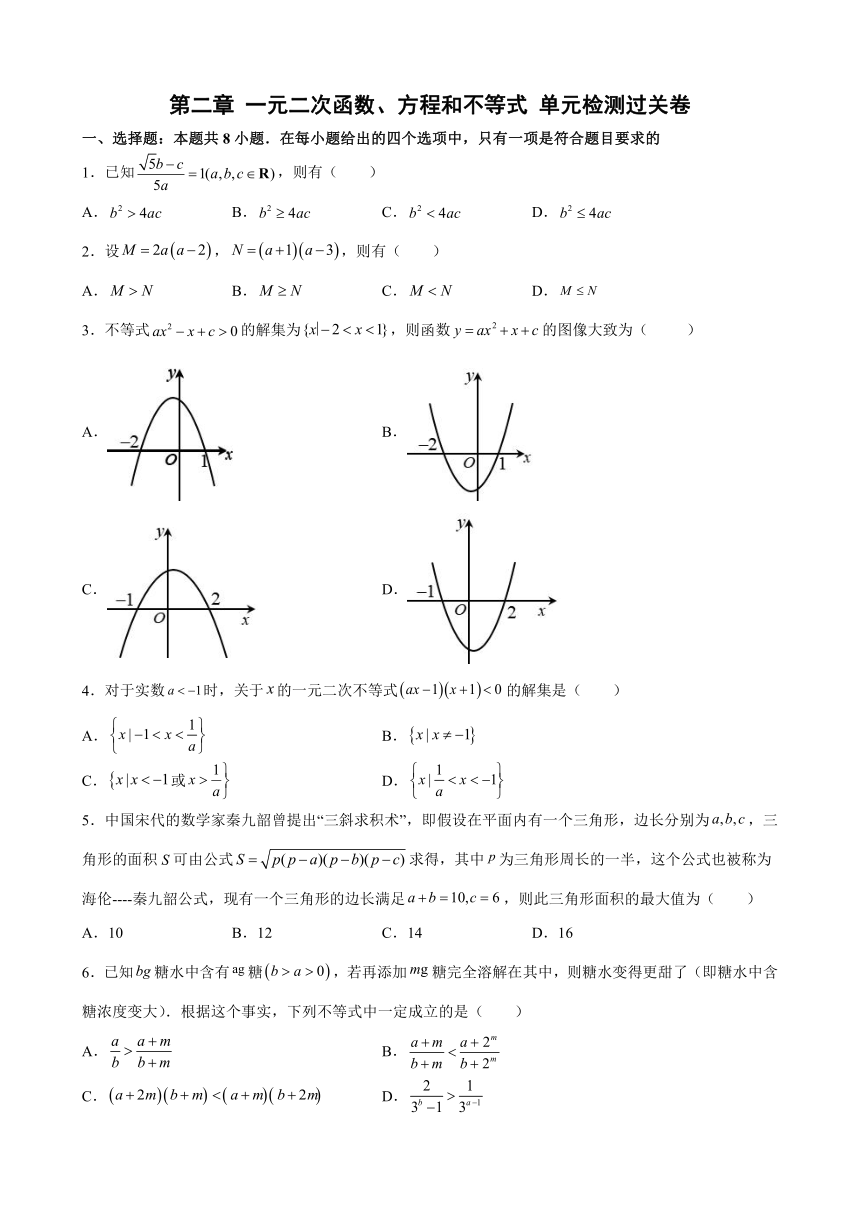 | |
| 格式 | docx | ||
| 文件大小 | 644.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 22:52:20 | ||
图片预览





文档简介
第二章 一元二次函数、方程和不等式 单元检测过关卷
一、选择题:本题共8小题.在每小题给出的四个选项中,只有一项是符合题目要求的
1.已知,则有( )
A. B. C. D.
2.设,,则有( )
A. B. C. D.
3.不等式的解集为,则函数的图像大致为( )
A. B.
C. D.
4.对于实数时,关于的一元二次不等式的解集是( )
A. B.
C.或 D.
5.中国宋代的数学家秦九韶曾提出“三斜求积术”,即假设在平面内有一个三角形,边长分别为,三角形的面积S可由公式求得,其中为三角形周长的一半,这个公式也被称为海伦----秦九韶公式,现有一个三角形的边长满足,则此三角形面积的最大值为( )
A.10 B.12 C.14 D.16
6.已知糖水中含有糖,若再添加糖完全溶解在其中,则糖水变得更甜了(即糖水中含糖浓度变大).根据这个事实,下列不等式中一定成立的是( )
A. B.
C. D.
7.若实数,,不等式恒成立,则正实数的最大值为( )
A. B. C. D.
8.商场若将进货单价为8元的商品按每件10元出售.每天可销售100件,现准备采用提高售价来增加利润.已知这种商品每件销售价提高1元,销售量就要减少10件.那么要保证每天所赚的利润在320元以上,销售价每件可定为( )
A.11元 B.16元
C.12元到16元之间 D.13元到15元之间
二、选择题:本题共4小题.在每小题给出的四个选项中,至少有一项是符合题目要求的
9.下列四个不等式中,解集为的是( )
A. B.
C. D.
10.若关于x的不等式0≤ax2+bx+c≤1(a>0)的解集为{x|-1≤x≤2},则3a+2b+c的值可以是( )
A. B. C. D.
11.已知关于x的不等式,下列结论正确的是( )
A.当时,不等式的解集为
B.当时,不等式的解集可以为的形式
C.不等式的解集恰好为,那么
D.不等式的解集恰好为,那么
12.已知函数()有且只有一个零点,则( )
A.
B.
C.若不等式的解集为(),则
D.若不等式的解集为(),且,则
三、填空题:本题共4小题
13.若不等式的解为,则实数a的取值范围是_____.
14.若,,则当______时,取得最小值.
15.一般情况下,不成立,但也有数可以使它成立,如.使得成立的一对数m、n我们称为“相伴数对”,记为(m,n).若(x,1)是“相伴数对”,则x的值为______.
16.在上定义运算,若关于的不等式的解集为,则实数的取值范围是_________.
四、解答题:本题共4小题,解答应写出文字说明、证明过程或演算步骤
17.已知不等式的解为或.
(1)求,的值;
(2)解关于的不等式:,其中是实数.
18.近日,随着新冠肺炎疫情在多地零星散发,一些城市陆续发出“春节期间非必要不返乡,就地过年”的倡议.为最大程度减少人员流动,减少疫情发生的可能性,某地政府积极制定政策,决定政企联动,鼓励企业在春节期间留住员工在本市过年并加班追产.为此,该地政府决定为当地某A企业春节期间加班追产提供(万元)的专项补贴.A企业在收到政府x(万元)补贴后,产量将增加到(万件).同时A企业生产t(万件)产品需要投入成本为(万元),并以每件元的价格将其生产的产品全部售出.注:收益=销售金额+政府专项补贴-成本
(1)求企业春节期间加班追产所获收益(万元)关于政府补贴(万元)的函数关系式;
(2)当政府的专项补贴为多少万元时,A企业春节期间加班追产所获收益最大?
19.证明不等式
(1)已知,证明:
(2)设,求证:
20.十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在大力实施一项将重塑全球汽车行业的计划,2020年某企业计划引进新能源汽车生产设备看,通过市场分析,全年需投入固定成本3000万元,每生产(百辆)需另投入成本(万元),且.由市场调研知,每辆车售价5万元,且全年内生产的车辆当年能全部销售完.
(1)求出2020年的利润(万元)关于年产量(百辆)的函数关系式;(利润=销售额—成本)
(2)当2020年产量为多少百辆时,企业所获利润最大?并求出最大利润.
21.设函数.
(1)当且时,解关于的不等式;
(2)已知,若的值域为,,求的最小值.
22.已知不等式的解集是.
(1)若,求的取值范围;
(2)若,求不等式的解集.
参考答案
1.B
【解析】解:由题意,∵
∴
∴,当且仅当时取等号;
∴
故选:B.
2.A
【解析】解:∵,
∴,
故选:A.
3.C
【解析】因为不等式的解集为,
故,故,故,
令,解得或,
故抛物线开口向下,与轴的交点的横坐标为,
故选:C.
4.C
【解析】因为,所以,所以的解集为或,
故选:C.
5.B
【解析】由题意,,,
可得,,
当且仅当时等号成立,
所以此三角形面积的最大值为12.
故选:.
6.B
【解析】对于A选项,由题意可知,A选项错误;
对于B选项,作出函数与的图象如下图所示:
由图可知,当时,,,则,
所以,,
即,B选项正确;
对于C选项,,
所以,,C选项错误;
对于D选项,取,,则,D选项错误.
故选:B.
7.D
【解析】由得
因为,,则
令
则化为恒成立,
由权方和不等式得
当且仅当,得即时等号成立.
所以
故选:D
8.C
【解析】设销售价定为每件元,利润为元,
则,
由题意可得:,
即, 所以,
解得:,
所以每件销售价应定为12元到16元之间,
故选:C
9.BD
【解析】A选项,,所以的解集不可能为空集;
B选项,,而开口向上,所以解集为空集;
C选项,的解集为,所以不为空集;
D选项,当且仅当 a = 2时等号成立,而开口向下,所以为空集;
故选:BD
10.BC
【解析】设其中a>0,
因为不等式0≤ax2+bx+c≤1(a>0)的解集为{x|-1≤x≤2},
所以恒大于等于零且,
故,即①,且②,③,
由②③可得
代入①,可得,
解得,
由知,
故,
结合选项,的值可能和,
故选:BC
11.AD
【解析】解:设,,则;
对于A:∵,∴当时,不等式的解集为,所以A正确;
对于B:在同一平面直角坐标系中作出函数y=x2-3x+4=(x-2)2+1的图象及直线y=a和y=b,如图所示:
由图知,当a=2时,不等式的解集为的形式,故B错误;
对于CD:由的图象知,若不等式的解集为连续不间断的区间,则,且;
若解集为,,则(a)(b),且,
因为,所以(b),解得或,
因为,所以,所以,所以,
所以C错误、D正确.
故选:AD
12.ABD
【解析】因为()有且只有一个零点,
故可得,即,
对A:等价于,显然,故正确;
对B:,故正确;
对C:因为不等式的解集为,
故可得,故错误;
对D:因为不等式的解集为,且,
则方程的两根为,,
故可得,
故可得,故D正确.
故选:ABD.
13.或.
【解析】由不等式的解为
可知,
即,
解得或.
14.##
【解析】∵,,∴,即,
①当时,,当且仅当时取等号,故当,取得最小值.
②当时,,当且仅当时取等号,故当时,取得最小值.
综上所述,当a的值为时,取得最小值,
故答案为:.
15.
【解析】由题意,得,
解得.
故答案为:
16.,
【解析】因为,不等式恒成立,
所以,不等式恒成立,
所以,不等式恒成立,
即,不等式恒成立,
所以,即,
解得:,
17.(1),;(2)答案见解析.
【解析】解:(1)依题意,
(2)原不等式为:,即
①当,即时,原不等式的解集为;
②当,即时,原不等式的解集为;
③当,即时,原不等式的解集为
18.(1);(2)即当政府的专项补贴为万元时,A企业春节期间加班追产所获收益最大,最大值为万元;
【解析】解:(1)依题意可知,销售金额万元,政府补贴万元,成本为万元;
所以收益,
(2)由(1)可知,
其中,当且仅当,即时取等号,
所以,
所以当时,A企业春节期间加班追产所获收益最大,最大值为万元;
即当政府的专项补贴为万元时,A企业春节期间加班追产所获收益最大,最大值为万元;
19.(1)证明见解析;(2)证明见解析.
【解析】(1),
当且仅当即时等号成立;
(2)因为
所以
当且仅当,, 时等号成立.
20.(1);(2)生产百辆时,该企业获得利润最大,且最大利润为万元.
【解析】(1)由题意,当时,
;
当时,
;
所以;
(2)当时,,
当且仅当时,;
当时,
(当且仅当,即时,“”成立)
因为,所以,当时,即年生产百辆时,该企业获得利润最大,且最大利润为万元.
21.(1)或;(2).
【解析】解:(1)由且,代入不等式,得,
化简,得,或,
不等式的解集为或
(2)由的值域为,,可得,△,
,可得.
,.
的最小值为.
22.(1);(2).
【解析】(1)∵,∴,∴
(2)∵,∴是方程的两个根,
∴由韦达定理得,解得,
∴不等式,即为:,
其解集为.
一、选择题:本题共8小题.在每小题给出的四个选项中,只有一项是符合题目要求的
1.已知,则有( )
A. B. C. D.
2.设,,则有( )
A. B. C. D.
3.不等式的解集为,则函数的图像大致为( )
A. B.
C. D.
4.对于实数时,关于的一元二次不等式的解集是( )
A. B.
C.或 D.
5.中国宋代的数学家秦九韶曾提出“三斜求积术”,即假设在平面内有一个三角形,边长分别为,三角形的面积S可由公式求得,其中为三角形周长的一半,这个公式也被称为海伦----秦九韶公式,现有一个三角形的边长满足,则此三角形面积的最大值为( )
A.10 B.12 C.14 D.16
6.已知糖水中含有糖,若再添加糖完全溶解在其中,则糖水变得更甜了(即糖水中含糖浓度变大).根据这个事实,下列不等式中一定成立的是( )
A. B.
C. D.
7.若实数,,不等式恒成立,则正实数的最大值为( )
A. B. C. D.
8.商场若将进货单价为8元的商品按每件10元出售.每天可销售100件,现准备采用提高售价来增加利润.已知这种商品每件销售价提高1元,销售量就要减少10件.那么要保证每天所赚的利润在320元以上,销售价每件可定为( )
A.11元 B.16元
C.12元到16元之间 D.13元到15元之间
二、选择题:本题共4小题.在每小题给出的四个选项中,至少有一项是符合题目要求的
9.下列四个不等式中,解集为的是( )
A. B.
C. D.
10.若关于x的不等式0≤ax2+bx+c≤1(a>0)的解集为{x|-1≤x≤2},则3a+2b+c的值可以是( )
A. B. C. D.
11.已知关于x的不等式,下列结论正确的是( )
A.当时,不等式的解集为
B.当时,不等式的解集可以为的形式
C.不等式的解集恰好为,那么
D.不等式的解集恰好为,那么
12.已知函数()有且只有一个零点,则( )
A.
B.
C.若不等式的解集为(),则
D.若不等式的解集为(),且,则
三、填空题:本题共4小题
13.若不等式的解为,则实数a的取值范围是_____.
14.若,,则当______时,取得最小值.
15.一般情况下,不成立,但也有数可以使它成立,如.使得成立的一对数m、n我们称为“相伴数对”,记为(m,n).若(x,1)是“相伴数对”,则x的值为______.
16.在上定义运算,若关于的不等式的解集为,则实数的取值范围是_________.
四、解答题:本题共4小题,解答应写出文字说明、证明过程或演算步骤
17.已知不等式的解为或.
(1)求,的值;
(2)解关于的不等式:,其中是实数.
18.近日,随着新冠肺炎疫情在多地零星散发,一些城市陆续发出“春节期间非必要不返乡,就地过年”的倡议.为最大程度减少人员流动,减少疫情发生的可能性,某地政府积极制定政策,决定政企联动,鼓励企业在春节期间留住员工在本市过年并加班追产.为此,该地政府决定为当地某A企业春节期间加班追产提供(万元)的专项补贴.A企业在收到政府x(万元)补贴后,产量将增加到(万件).同时A企业生产t(万件)产品需要投入成本为(万元),并以每件元的价格将其生产的产品全部售出.注:收益=销售金额+政府专项补贴-成本
(1)求企业春节期间加班追产所获收益(万元)关于政府补贴(万元)的函数关系式;
(2)当政府的专项补贴为多少万元时,A企业春节期间加班追产所获收益最大?
19.证明不等式
(1)已知,证明:
(2)设,求证:
20.十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在大力实施一项将重塑全球汽车行业的计划,2020年某企业计划引进新能源汽车生产设备看,通过市场分析,全年需投入固定成本3000万元,每生产(百辆)需另投入成本(万元),且.由市场调研知,每辆车售价5万元,且全年内生产的车辆当年能全部销售完.
(1)求出2020年的利润(万元)关于年产量(百辆)的函数关系式;(利润=销售额—成本)
(2)当2020年产量为多少百辆时,企业所获利润最大?并求出最大利润.
21.设函数.
(1)当且时,解关于的不等式;
(2)已知,若的值域为,,求的最小值.
22.已知不等式的解集是.
(1)若,求的取值范围;
(2)若,求不等式的解集.
参考答案
1.B
【解析】解:由题意,∵
∴
∴,当且仅当时取等号;
∴
故选:B.
2.A
【解析】解:∵,
∴,
故选:A.
3.C
【解析】因为不等式的解集为,
故,故,故,
令,解得或,
故抛物线开口向下,与轴的交点的横坐标为,
故选:C.
4.C
【解析】因为,所以,所以的解集为或,
故选:C.
5.B
【解析】由题意,,,
可得,,
当且仅当时等号成立,
所以此三角形面积的最大值为12.
故选:.
6.B
【解析】对于A选项,由题意可知,A选项错误;
对于B选项,作出函数与的图象如下图所示:
由图可知,当时,,,则,
所以,,
即,B选项正确;
对于C选项,,
所以,,C选项错误;
对于D选项,取,,则,D选项错误.
故选:B.
7.D
【解析】由得
因为,,则
令
则化为恒成立,
由权方和不等式得
当且仅当,得即时等号成立.
所以
故选:D
8.C
【解析】设销售价定为每件元,利润为元,
则,
由题意可得:,
即, 所以,
解得:,
所以每件销售价应定为12元到16元之间,
故选:C
9.BD
【解析】A选项,,所以的解集不可能为空集;
B选项,,而开口向上,所以解集为空集;
C选项,的解集为,所以不为空集;
D选项,当且仅当 a = 2时等号成立,而开口向下,所以为空集;
故选:BD
10.BC
【解析】设其中a>0,
因为不等式0≤ax2+bx+c≤1(a>0)的解集为{x|-1≤x≤2},
所以恒大于等于零且,
故,即①,且②,③,
由②③可得
代入①,可得,
解得,
由知,
故,
结合选项,的值可能和,
故选:BC
11.AD
【解析】解:设,,则;
对于A:∵,∴当时,不等式的解集为,所以A正确;
对于B:在同一平面直角坐标系中作出函数y=x2-3x+4=(x-2)2+1的图象及直线y=a和y=b,如图所示:
由图知,当a=2时,不等式的解集为的形式,故B错误;
对于CD:由的图象知,若不等式的解集为连续不间断的区间,则,且;
若解集为,,则(a)(b),且,
因为,所以(b),解得或,
因为,所以,所以,所以,
所以C错误、D正确.
故选:AD
12.ABD
【解析】因为()有且只有一个零点,
故可得,即,
对A:等价于,显然,故正确;
对B:,故正确;
对C:因为不等式的解集为,
故可得,故错误;
对D:因为不等式的解集为,且,
则方程的两根为,,
故可得,
故可得,故D正确.
故选:ABD.
13.或.
【解析】由不等式的解为
可知,
即,
解得或.
14.##
【解析】∵,,∴,即,
①当时,,当且仅当时取等号,故当,取得最小值.
②当时,,当且仅当时取等号,故当时,取得最小值.
综上所述,当a的值为时,取得最小值,
故答案为:.
15.
【解析】由题意,得,
解得.
故答案为:
16.,
【解析】因为,不等式恒成立,
所以,不等式恒成立,
所以,不等式恒成立,
即,不等式恒成立,
所以,即,
解得:,
17.(1),;(2)答案见解析.
【解析】解:(1)依题意,
(2)原不等式为:,即
①当,即时,原不等式的解集为;
②当,即时,原不等式的解集为;
③当,即时,原不等式的解集为
18.(1);(2)即当政府的专项补贴为万元时,A企业春节期间加班追产所获收益最大,最大值为万元;
【解析】解:(1)依题意可知,销售金额万元,政府补贴万元,成本为万元;
所以收益,
(2)由(1)可知,
其中,当且仅当,即时取等号,
所以,
所以当时,A企业春节期间加班追产所获收益最大,最大值为万元;
即当政府的专项补贴为万元时,A企业春节期间加班追产所获收益最大,最大值为万元;
19.(1)证明见解析;(2)证明见解析.
【解析】(1),
当且仅当即时等号成立;
(2)因为
所以
当且仅当,, 时等号成立.
20.(1);(2)生产百辆时,该企业获得利润最大,且最大利润为万元.
【解析】(1)由题意,当时,
;
当时,
;
所以;
(2)当时,,
当且仅当时,;
当时,
(当且仅当,即时,“”成立)
因为,所以,当时,即年生产百辆时,该企业获得利润最大,且最大利润为万元.
21.(1)或;(2).
【解析】解:(1)由且,代入不等式,得,
化简,得,或,
不等式的解集为或
(2)由的值域为,,可得,△,
,可得.
,.
的最小值为.
22.(1);(2).
【解析】(1)∵,∴,∴
(2)∵,∴是方程的两个根,
∴由韦达定理得,解得,
∴不等式,即为:,
其解集为.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
