苏科版七下数学9.4(1)完全平方公式 课件(18张ppt)
文档属性
| 名称 | 苏科版七下数学9.4(1)完全平方公式 课件(18张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 461.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-18 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
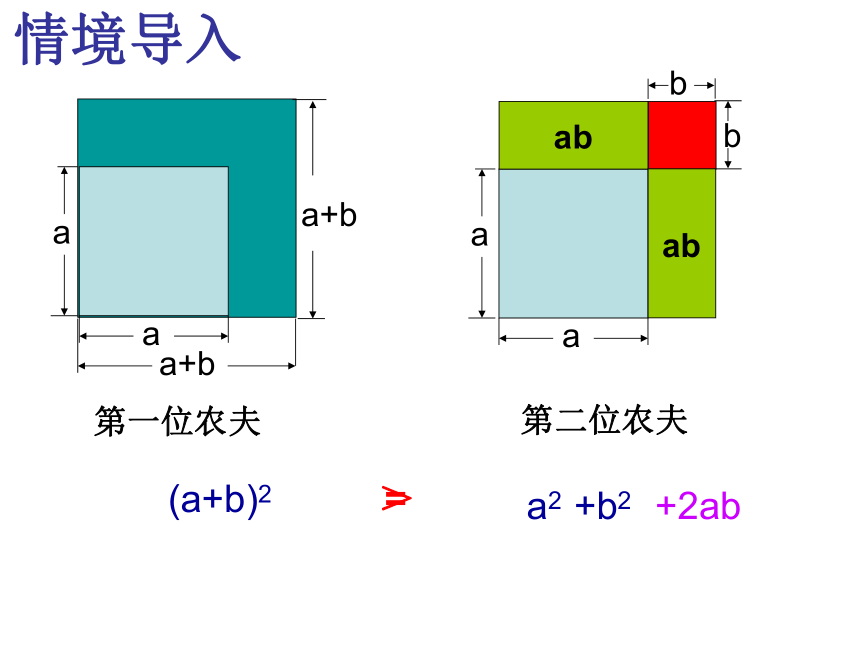
情境导入
a+b
a+b
第一位农夫
a
a
a
第二位农夫
a
b
b
(a+b)2
a2
>
第二位农夫
ab
ab
=
+2ab
+b2
情境导入
a+b
a+b
第一位农夫
a
a
a
第二位农夫
a
b
b
(a+b)2
a2
第二位农夫
ab
ab
=
+2ab
+b2
数学思考
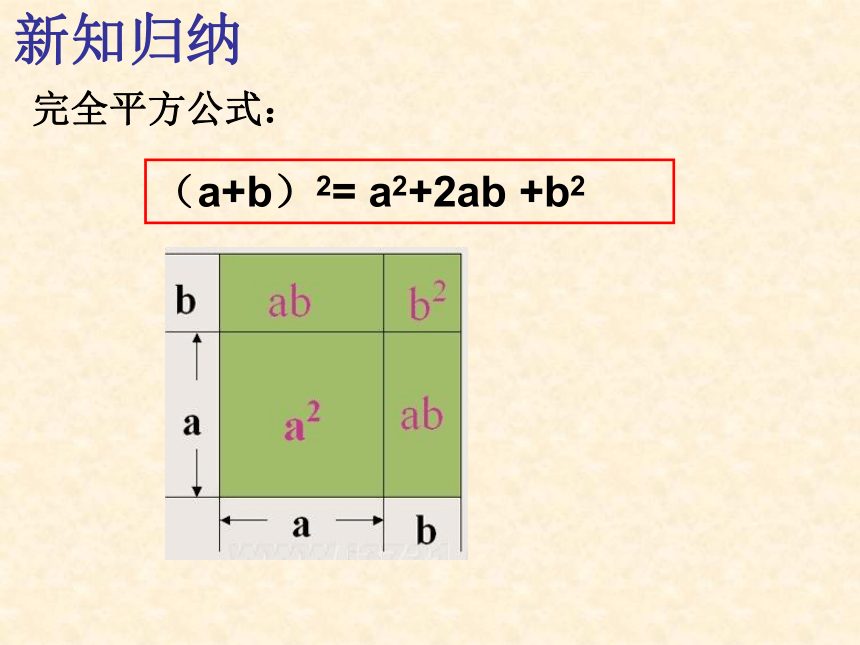
(a+b)2= a2+2ab +b2
新知归纳
完全平方公式:
合作学习
计算
合作学习
计算
(a-b)2
= (a-b)(a-b)
= a2-2ab +b2
= a2-ab-ba+b2
合作学习
计算
合作学习
计算
(a-b)2
= (a-b)(a-b)
= a2-2ab +b2
= a2-ab-ba+b2
(a-b)2= a2-2ab +b2
新知归纳
完全平方公式:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
两个数的和的平方等于这两个数的平方和与它们积的2倍的和.
两个数的差的平方等于这两个数的平方和与它们积的2倍的差.
例1:用完全平方公式计算:
(1)(x+2y)2;(2)
典型例题
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
练习1:用完全平方公式计算
(1)(4+3p)2;(2)(2x-3y)2
典型例题
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
例2:用完全平方公式计算
(1)(-1.1x+3y)2; (2)
练习2:1、用完全平方公式计算
(1)(-2m-3n)2
(2)
2、判断并改错
×
×
×
2、判断并改错
×
√
×
例3:简便计算 (1)3022 (2)49.72
典型例题
解:
课堂小结
完全平方公式
应用与拓展
面积恒等法
多项式相乘法则
数形结合思想
一题多解方法
1.整理
2.公式选择
3.代入准确
4.化简
转化思想
拓展提高
通过本节课的学习你会求(a+b+c)2的值吗?
说说你的方法。
拓展提高
填空:
2b
b
2y
4y2
1
2x
巩固练习
1、填空
(1)(-2a+b)2=_______ ;(2)(-2a-b)2=_______;
(3)(0.2x+___)2=____+2x+______
(4)(______+1)2=
+_____+ .
2、计算
(1)(1+x)2(2)(y-4)2(3)
(4) (-3x-2)2(5)20212
3、已知a+b=2,ab=1, 求a2+b2、(a-b)2的值.
情境导入
a+b
a+b
第一位农夫
a
a
a
第二位农夫
a
b
b
(a+b)2
a2
>
第二位农夫
ab
ab
=
+2ab
+b2
情境导入
a+b
a+b
第一位农夫
a
a
a
第二位农夫
a
b
b
(a+b)2
a2
第二位农夫
ab
ab
=
+2ab
+b2
数学思考
(a+b)2= a2+2ab +b2
新知归纳
完全平方公式:
合作学习
计算
合作学习
计算
(a-b)2
= (a-b)(a-b)
= a2-2ab +b2
= a2-ab-ba+b2
合作学习
计算
合作学习
计算
(a-b)2
= (a-b)(a-b)
= a2-2ab +b2
= a2-ab-ba+b2
(a-b)2= a2-2ab +b2
新知归纳
完全平方公式:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
两个数的和的平方等于这两个数的平方和与它们积的2倍的和.
两个数的差的平方等于这两个数的平方和与它们积的2倍的差.
例1:用完全平方公式计算:
(1)(x+2y)2;(2)
典型例题
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
练习1:用完全平方公式计算
(1)(4+3p)2;(2)(2x-3y)2
典型例题
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
例2:用完全平方公式计算
(1)(-1.1x+3y)2; (2)
练习2:1、用完全平方公式计算
(1)(-2m-3n)2
(2)
2、判断并改错
×
×
×
2、判断并改错
×
√
×
例3:简便计算 (1)3022 (2)49.72
典型例题
解:
课堂小结
完全平方公式
应用与拓展
面积恒等法
多项式相乘法则
数形结合思想
一题多解方法
1.整理
2.公式选择
3.代入准确
4.化简
转化思想
拓展提高
通过本节课的学习你会求(a+b+c)2的值吗?
说说你的方法。
拓展提高
填空:
2b
b
2y
4y2
1
2x
巩固练习
1、填空
(1)(-2a+b)2=_______ ;(2)(-2a-b)2=_______;
(3)(0.2x+___)2=____+2x+______
(4)(______+1)2=
+_____+ .
2、计算
(1)(1+x)2(2)(y-4)2(3)
(4) (-3x-2)2(5)20212
3、已知a+b=2,ab=1, 求a2+b2、(a-b)2的值.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
