【中考数学培优复习考点专题突破】专题10 二次函数(考点讲解)(含解析)
文档属性
| 名称 | 【中考数学培优复习考点专题突破】专题10 二次函数(考点讲解)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-19 09:16:57 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2021年中考数学培优复习考点专题突破 第三章 函数及其图象
专题10 二次函数
【考纲要求】
1.理解二次函数的有关概念.2.会用描点法画二次函数的图象,能从图象上认识二次函数的性质.3.会根据公式确定图象的顶点、开口方向和对称轴,并能掌握二次函数图象的平移.21世纪教育网4.熟练掌握二次函数解析式的求法,并能用它解决有关的实际问题.5.会用二次函数的图象求一元二次方程的近似解.
【备考指南】
二次函数是中考的重点内容,题型主 ( http: / / www.21cnjy.com )要有选择题、填空题及解答题,而且常与方程、不等式、几何知识等结合在一起综合考查,且一般为压轴题.中考命题不仅考查二次函数的概念、图象和性质等基础知识,而且注重多个知识点的综合考查以及对学生应用二次函数解决实际问题能力的考查.
【考点总结】一、二次函数的概念
一般地,如果y=ax2+bx+c(a,b,c是常数,a≠0),那么y叫做x的二次函数.
注意:(1)二次项系数a≠0;
(2)ax2+bx+c必须是整式;
(3)一次项可以为零,常数项也可以为零,一次项和常数项可以同时为零;
(4)自变量x的取值范围是全体实数.
【考点总结】二、二次函数的图象及性质
二次函数y=ax2+bx+c(a,b,c为常数,a≠0)
图象 ( http: / / www.21cnjy.com / )(a>0) ( http: / / www.21cnjy.com / )(a<0)
开口方向 开口向上 开口向下
对称轴 直线x=- 直线x=-
顶点坐标
增减性 当x<-时,y随x的增大而减小;当x>-时,y随x的增大而增大 当x<-时,y随x的增大而增大;当x>-时,y随x的增大而减小
最值 当x=-时,y有最小值 当x=-时,y有最大值
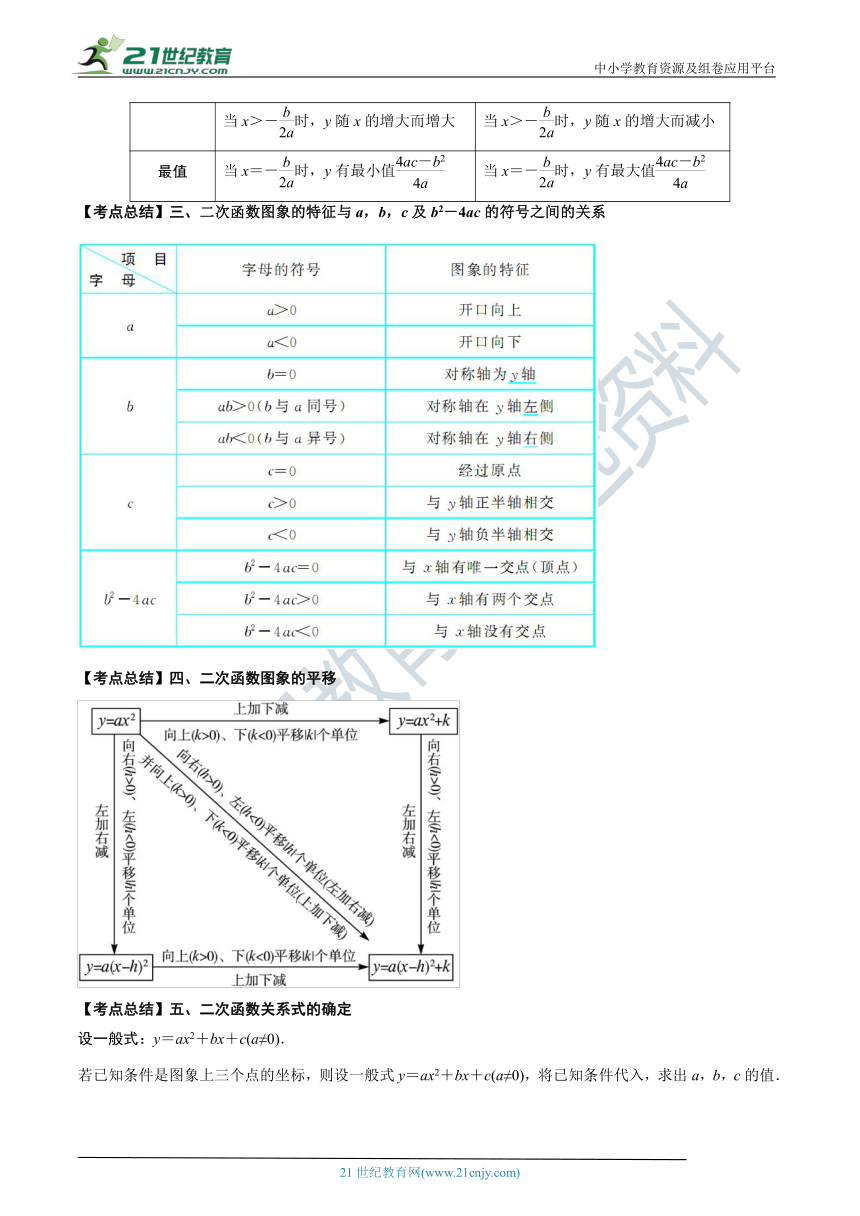
【考点总结】三、二次函数图象的特征与a,b,c及b2-4ac的符号之间的关系
( http: / / www.21cnjy.com / )
【考点总结】四、二次函数图象的平移
( http: / / www.21cnjy.com / )
【考点总结】五、二次函数关系式的确定
设一般式:y=ax2+bx+c(a≠0).
若已知条件是图象上三个点的坐标,则设一般式y=ax2+bx+c(a≠0),将已知条件代入,求出a,b,c的值.
【考点总结】六、二次函数与一元二次方程的关系
1.二次函数y=ax2+bx+c(a≠0),当y=0时,就变成了ax2+bx+c=0(a≠0).[
2.ax2+bx+c=0(a≠0)的解是抛物线与x轴交点的横坐标.
3.当Δ=b2-4ac>0时,抛物线与x轴有两个不同的交点;
当Δ=b2-4ac=0时,抛物线与x轴有一个交点;
当Δ=b2-4ac<0时,抛物线与x轴没有交点.
【考点】一、二次函数的图象及性质
例1、(1)二次函数y=-3x2-6x+5的图象的顶点坐标是( ).
A.(-1,8) B.(1,8) C.(-1,2) D.(1,-4)
(2)已知抛物线y=ax2+bx+c(a>0 ( http: / / www.21cnjy.com ))的对称轴为直线x=1,且经过点(-1,y1),(2,y2),试比较y1和y2的大小:y1________y2.(填“>”“<”或“=”)21教育网
解析:(1)抛物线的顶点坐标可以利用顶点坐标公式或配方法来求.
∵-=-=-1,
==8.
∴二次函数y=-3x2-6x+5的图象的顶点坐标是(-1,8).
(2)点(-1,y1),(2,y2)不在 ( http: / / www.21cnjy.com )对称轴的同一侧,不能直接利用二次函数的增减性来判断y1,y2的大小,可先根据抛物线关于对称轴的对称性,然后再用二次函数的增减性即可.设抛物线经过点(0,y3),∵抛物线对称轴为直线x=1,www.21-cn-jy.com
∴点(0,y3)与点(2,y2)关于直线x=1对称.∴y3=y2.
∵a>0,∴当x<1时,y随x的增大而减小.
∴y1>y3.∴y1>y2.
答案:(1)A (2)>
1.将抛物线解析式写成y=a ( http: / / www.21cnjy.com )(x-h)2+k的形式,则顶点坐标为(h,k),对称轴为直线x=h,也可应用对称轴公式x=-,顶点坐标来求顶点坐标及对称轴.2·1·c·n·j·y
2.比较两个二次函数值大小的方法:
(1)直接代入自变量求值法;
(2)当自变量在对称轴两侧时,看两个数到对称轴的距离及函数值的增减性判断;
(3)当自变量在对称轴同侧时,根据函数值的增减性判断.
【考点】二、利用二次函数图象判断a,b,c的符号
例2、如图所示,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴交于负半轴.【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
(1)给出四个结论:①a>0;②b>0;③c>0;④a+b+c=0,其中正确结论的序号是_________;
(2)给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.其中正确结论的序号是_______.
解析:(1)∵抛物线开口向上,∴a>0;
∵对称轴在y轴右侧,∴->0,∴b<0;
与y轴的交点在x轴下方,∴c<0;
当x=1时,y=0,∴a+b+c=0,故填①④.
(2)由(1)问知a>0,b<0,c<0,∴abc>0;
又知-<1,∴2a+b>0;
又知x=1时,y=0;x=-1时,y=2,
∴∴a+c=1;
又知c<0,∴a=1-c>1,故填②③④
答案:(1)①④ (2)②③④
根据二次函数的图象确定有关代数式的符号,是二 ( http: / / www.21cnjy.com )次函数中的一类典型的数形结合问题,具有较强的推理性.解题时应注意开口方向与a的关系,抛物线与y轴的交点与c的关系,对称轴与a,b的关系,抛物线与x轴交点数目与b2-4ac的符号的关系;当x=1时,决定a+b+c的符号,当x=-1时,决定a-b+c的符号.在此基础上,还可推出其他代数式的符号.运用数形结合的思想更直观、更简捷.21cnjy.com
【考点】三、二次函数图象的平移
例3、二次函数y=-2x2+4x+1的图象怎样平移得到y=-2x2的图象( ).
A.向左平移1个单位,再向上平移3个单位
B.向右平移1个单位,再向上平移3个单位
C.向左平移1个单位,再向下平移3个单位
D.向右平移1个单位,再向下平移3个单位
解析:首先将二次函数的解析式配方化为 ( http: / / www.21cnjy.com )顶点式,然后确定如何平移,即y=-2x2+4x+1=-2(x-1)2+3,将该函数图象向左平移1个单位,再向下平移3个单位就得到y=-2x2的图象.21·cn·jy·com
答案:C
二次函数图象的平移实际上就是顶点 ( http: / / www.21cnjy.com )位置的变换,因此先将二次函数解析式转化为顶点式确定其顶点坐标,然后按照“左加右减、上加下减”的规律进行操作.www-2-1-cnjy-com
【考点】四、确定二次函数的解析式
例4、已知一抛物线与x轴的交点是A(-2,0),B(1,0),且经过点C(2,8).
(1)求该抛物线的表达式;
(2)求该抛物线的顶点坐标.
解:(1)设这个抛物线的表达式为y=ax2+bx+C.
由已知抛物线经过A(-2,0),B(1,0),C(2,8)三点,
得解这个方程组,得
所以所求抛物线的表达式为y=2x2+2x-4.
(2)y=2x2+2x-4=22-,
所以该抛物线的顶点坐标是.
用待定系数法求二次函数解析式,根据已知条件,用图象上三个点的坐标,设一般式求解.
【考点】五、二次函数的实际应用
例5、某商品的进价为每件 ( http: / / www.21cnjy.com )40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.21世纪教育网版权所有
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)每件商品的售价定为多少元时, ( http: / / www.21cnjy.com )每个月的利润恰为2 200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2 200元?21·世纪*教育网
解:(1)y=(210-10x)(50+x-40)=-10x2+110x+2 100(0<x≤15且x为整数);2-1-c-n-j-y
(2)y=-10(x-5.5)2+2 402.5.∵a=-10<0,
∴当x=5.5时,y有最大值2 402.5.
∵0<x≤15,且x为整数,
当x=5时,50+x=55,y=2 400(元),当x=6时,50+x=56,y=2 400(元),21*cnjy*com
∴当售价定为每件55或56元时,每个月的利润最大,最大的月利润是2 400元.
(3)当y=2 200时,-10x2+110x+2 100=2 200,解得x1=1,x2=10.
∴当x=1时,50+x=51,当x=10时,50+x=60.
∴当售价定为每件51或60元时,每个月的利润为2 200元.
当售价不低于51元且不高于6 ( http: / / www.21cnjy.com )0元且为整数时,每个月的利润不低于2 200元(或当售价分别为51,52,53,54,55,56,57,58,59,60元时,每个月的利润不低于2 200元).【来源:21cnj*y.co*m】
运用二次函数的性质解决生活和实际生产中的最大值和最小值问题是最常见的题目类型,解决这类问题的方法是:【出处:21教育名师】
1.列出二次函数的关系式,列关系式时,要根据自变量的实际意义,确定自变量的取值范围.
2.在自变量取值范围内,运用公式法或配方法求出二次函数的最大值和最小值.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2021年中考数学培优复习考点专题突破 第三章 函数及其图象
专题10 二次函数
【考纲要求】
1.理解二次函数的有关概念.2.会用描点法画二次函数的图象,能从图象上认识二次函数的性质.3.会根据公式确定图象的顶点、开口方向和对称轴,并能掌握二次函数图象的平移.21世纪教育网4.熟练掌握二次函数解析式的求法,并能用它解决有关的实际问题.5.会用二次函数的图象求一元二次方程的近似解.
【备考指南】
二次函数是中考的重点内容,题型主 ( http: / / www.21cnjy.com )要有选择题、填空题及解答题,而且常与方程、不等式、几何知识等结合在一起综合考查,且一般为压轴题.中考命题不仅考查二次函数的概念、图象和性质等基础知识,而且注重多个知识点的综合考查以及对学生应用二次函数解决实际问题能力的考查.
【考点总结】一、二次函数的概念
一般地,如果y=ax2+bx+c(a,b,c是常数,a≠0),那么y叫做x的二次函数.
注意:(1)二次项系数a≠0;
(2)ax2+bx+c必须是整式;
(3)一次项可以为零,常数项也可以为零,一次项和常数项可以同时为零;
(4)自变量x的取值范围是全体实数.
【考点总结】二、二次函数的图象及性质
二次函数y=ax2+bx+c(a,b,c为常数,a≠0)
图象 ( http: / / www.21cnjy.com / )(a>0) ( http: / / www.21cnjy.com / )(a<0)
开口方向 开口向上 开口向下
对称轴 直线x=- 直线x=-
顶点坐标
增减性 当x<-时,y随x的增大而减小;当x>-时,y随x的增大而增大 当x<-时,y随x的增大而增大;当x>-时,y随x的增大而减小
最值 当x=-时,y有最小值 当x=-时,y有最大值
【考点总结】三、二次函数图象的特征与a,b,c及b2-4ac的符号之间的关系
( http: / / www.21cnjy.com / )
【考点总结】四、二次函数图象的平移
( http: / / www.21cnjy.com / )
【考点总结】五、二次函数关系式的确定
设一般式:y=ax2+bx+c(a≠0).
若已知条件是图象上三个点的坐标,则设一般式y=ax2+bx+c(a≠0),将已知条件代入,求出a,b,c的值.
【考点总结】六、二次函数与一元二次方程的关系
1.二次函数y=ax2+bx+c(a≠0),当y=0时,就变成了ax2+bx+c=0(a≠0).[
2.ax2+bx+c=0(a≠0)的解是抛物线与x轴交点的横坐标.
3.当Δ=b2-4ac>0时,抛物线与x轴有两个不同的交点;
当Δ=b2-4ac=0时,抛物线与x轴有一个交点;
当Δ=b2-4ac<0时,抛物线与x轴没有交点.
【考点】一、二次函数的图象及性质
例1、(1)二次函数y=-3x2-6x+5的图象的顶点坐标是( ).
A.(-1,8) B.(1,8) C.(-1,2) D.(1,-4)
(2)已知抛物线y=ax2+bx+c(a>0 ( http: / / www.21cnjy.com ))的对称轴为直线x=1,且经过点(-1,y1),(2,y2),试比较y1和y2的大小:y1________y2.(填“>”“<”或“=”)21教育网
解析:(1)抛物线的顶点坐标可以利用顶点坐标公式或配方法来求.
∵-=-=-1,
==8.
∴二次函数y=-3x2-6x+5的图象的顶点坐标是(-1,8).
(2)点(-1,y1),(2,y2)不在 ( http: / / www.21cnjy.com )对称轴的同一侧,不能直接利用二次函数的增减性来判断y1,y2的大小,可先根据抛物线关于对称轴的对称性,然后再用二次函数的增减性即可.设抛物线经过点(0,y3),∵抛物线对称轴为直线x=1,www.21-cn-jy.com
∴点(0,y3)与点(2,y2)关于直线x=1对称.∴y3=y2.
∵a>0,∴当x<1时,y随x的增大而减小.
∴y1>y3.∴y1>y2.
答案:(1)A (2)>
1.将抛物线解析式写成y=a ( http: / / www.21cnjy.com )(x-h)2+k的形式,则顶点坐标为(h,k),对称轴为直线x=h,也可应用对称轴公式x=-,顶点坐标来求顶点坐标及对称轴.2·1·c·n·j·y
2.比较两个二次函数值大小的方法:
(1)直接代入自变量求值法;
(2)当自变量在对称轴两侧时,看两个数到对称轴的距离及函数值的增减性判断;
(3)当自变量在对称轴同侧时,根据函数值的增减性判断.
【考点】二、利用二次函数图象判断a,b,c的符号
例2、如图所示,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴交于负半轴.【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
(1)给出四个结论:①a>0;②b>0;③c>0;④a+b+c=0,其中正确结论的序号是_________;
(2)给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.其中正确结论的序号是_______.
解析:(1)∵抛物线开口向上,∴a>0;
∵对称轴在y轴右侧,∴->0,∴b<0;
与y轴的交点在x轴下方,∴c<0;
当x=1时,y=0,∴a+b+c=0,故填①④.
(2)由(1)问知a>0,b<0,c<0,∴abc>0;
又知-<1,∴2a+b>0;
又知x=1时,y=0;x=-1时,y=2,
∴∴a+c=1;
又知c<0,∴a=1-c>1,故填②③④
答案:(1)①④ (2)②③④
根据二次函数的图象确定有关代数式的符号,是二 ( http: / / www.21cnjy.com )次函数中的一类典型的数形结合问题,具有较强的推理性.解题时应注意开口方向与a的关系,抛物线与y轴的交点与c的关系,对称轴与a,b的关系,抛物线与x轴交点数目与b2-4ac的符号的关系;当x=1时,决定a+b+c的符号,当x=-1时,决定a-b+c的符号.在此基础上,还可推出其他代数式的符号.运用数形结合的思想更直观、更简捷.21cnjy.com
【考点】三、二次函数图象的平移
例3、二次函数y=-2x2+4x+1的图象怎样平移得到y=-2x2的图象( ).
A.向左平移1个单位,再向上平移3个单位
B.向右平移1个单位,再向上平移3个单位
C.向左平移1个单位,再向下平移3个单位
D.向右平移1个单位,再向下平移3个单位
解析:首先将二次函数的解析式配方化为 ( http: / / www.21cnjy.com )顶点式,然后确定如何平移,即y=-2x2+4x+1=-2(x-1)2+3,将该函数图象向左平移1个单位,再向下平移3个单位就得到y=-2x2的图象.21·cn·jy·com
答案:C
二次函数图象的平移实际上就是顶点 ( http: / / www.21cnjy.com )位置的变换,因此先将二次函数解析式转化为顶点式确定其顶点坐标,然后按照“左加右减、上加下减”的规律进行操作.www-2-1-cnjy-com
【考点】四、确定二次函数的解析式
例4、已知一抛物线与x轴的交点是A(-2,0),B(1,0),且经过点C(2,8).
(1)求该抛物线的表达式;
(2)求该抛物线的顶点坐标.
解:(1)设这个抛物线的表达式为y=ax2+bx+C.
由已知抛物线经过A(-2,0),B(1,0),C(2,8)三点,
得解这个方程组,得
所以所求抛物线的表达式为y=2x2+2x-4.
(2)y=2x2+2x-4=22-,
所以该抛物线的顶点坐标是.
用待定系数法求二次函数解析式,根据已知条件,用图象上三个点的坐标,设一般式求解.
【考点】五、二次函数的实际应用
例5、某商品的进价为每件 ( http: / / www.21cnjy.com )40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.21世纪教育网版权所有
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)每件商品的售价定为多少元时, ( http: / / www.21cnjy.com )每个月的利润恰为2 200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2 200元?21·世纪*教育网
解:(1)y=(210-10x)(50+x-40)=-10x2+110x+2 100(0<x≤15且x为整数);2-1-c-n-j-y
(2)y=-10(x-5.5)2+2 402.5.∵a=-10<0,
∴当x=5.5时,y有最大值2 402.5.
∵0<x≤15,且x为整数,
当x=5时,50+x=55,y=2 400(元),当x=6时,50+x=56,y=2 400(元),21*cnjy*com
∴当售价定为每件55或56元时,每个月的利润最大,最大的月利润是2 400元.
(3)当y=2 200时,-10x2+110x+2 100=2 200,解得x1=1,x2=10.
∴当x=1时,50+x=51,当x=10时,50+x=60.
∴当售价定为每件51或60元时,每个月的利润为2 200元.
当售价不低于51元且不高于6 ( http: / / www.21cnjy.com )0元且为整数时,每个月的利润不低于2 200元(或当售价分别为51,52,53,54,55,56,57,58,59,60元时,每个月的利润不低于2 200元).【来源:21cnj*y.co*m】
运用二次函数的性质解决生活和实际生产中的最大值和最小值问题是最常见的题目类型,解决这类问题的方法是:【出处:21教育名师】
1.列出二次函数的关系式,列关系式时,要根据自变量的实际意义,确定自变量的取值范围.
2.在自变量取值范围内,运用公式法或配方法求出二次函数的最大值和最小值.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
