高一数学《第二章基本初等函数(Ⅰ) 》复习课件
文档属性
| 名称 | 高一数学《第二章基本初等函数(Ⅰ) 》复习课件 |  | |
| 格式 | zip | ||
| 文件大小 | 141.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-24 07:48:07 | ||
图片预览





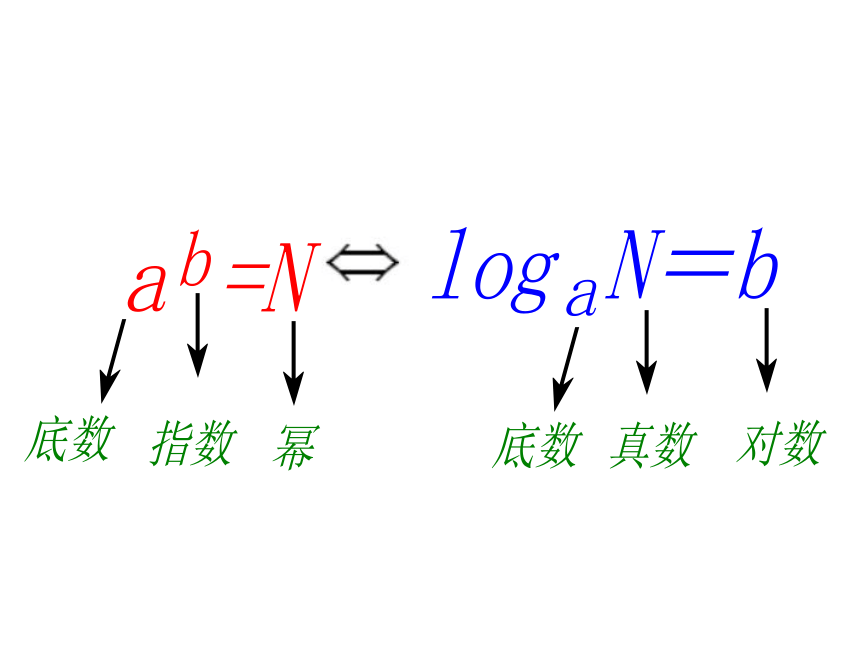
文档简介
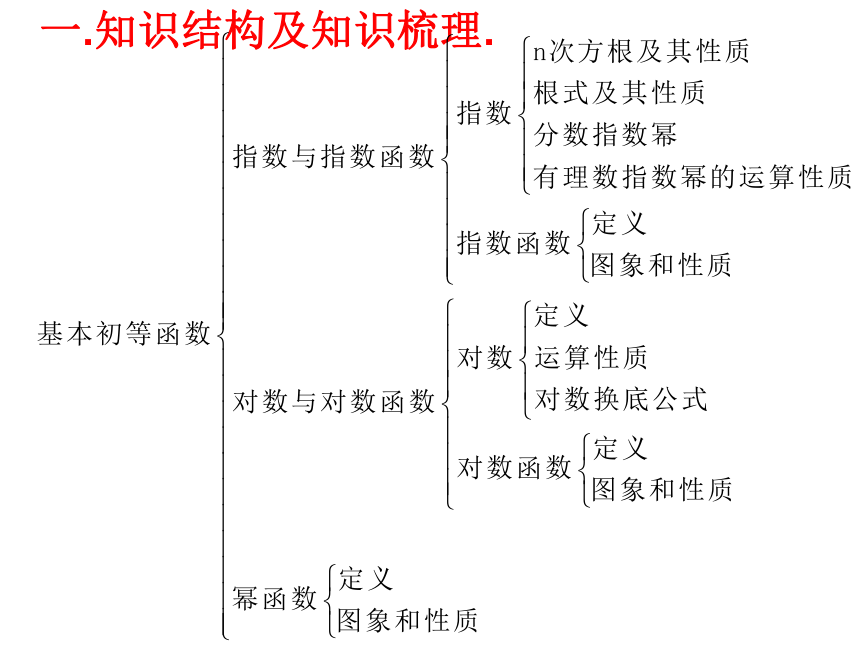
课件22张PPT。 第二章复习一.知识结构及知识梳理.1.根式的运算性质: 2.正数的正分数指数幂的意义:3.负分数指数幂: 4.0的正分数指数幂等于0,0的负分数指数幂没有意义1.指数函数概念
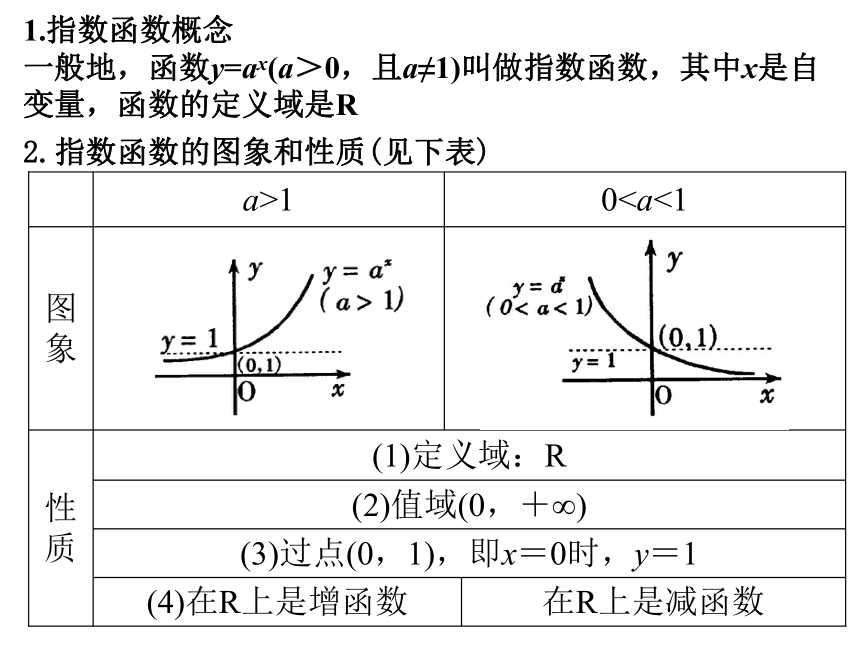
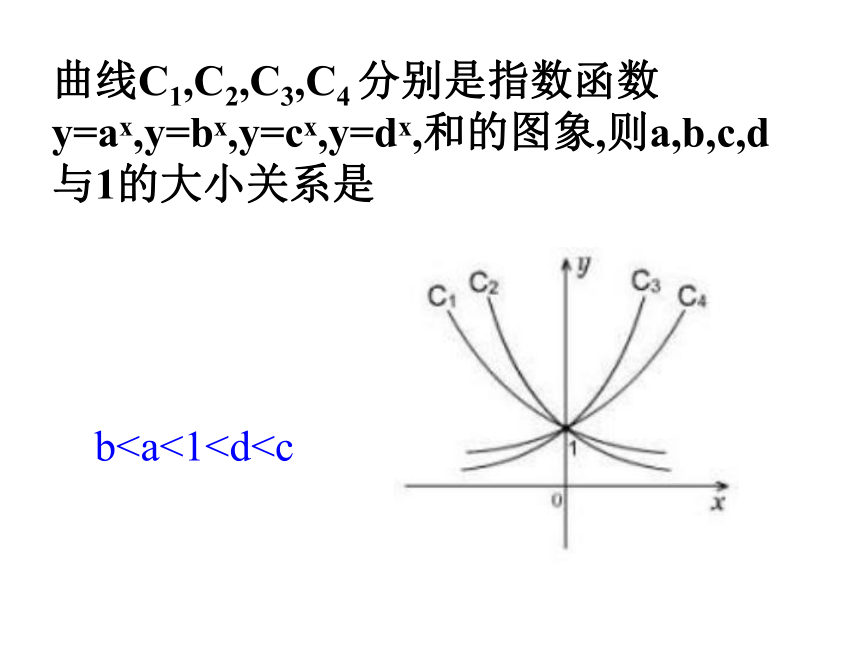
一般地,函数y=ax(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R2.指数函数的图象和性质(见下表)曲线C1,C2,C3,C4 分别是指数函数y=ax,y=bx,y=cx,y=dx,和的图象,则a,b,c,d与1的大小关系是 b2.函数y=f(x+a)的图象可以由函数y=f(x)的图象平移 个单位得到,a>0时,向 (左,右)平移,a<0时,向 (左,右)平移.
3.可知y=f(x)+a的图象可由y=f(x) 得到,a>0时,向 (上,下)平移,a<0时,向 (上,下)平移。 一、对数的定义: 一般地,如果 的b次幂等于N, 即 (叫指数式), 那么数 b叫做 a为底N的对数 记作 (叫对数式),a叫做对数的底数, N叫做真数 三.几个常用结论:(1)负数与零没有对数 (1)常用对数:通常将以10为底的对数
叫做常用对数(common logarithm)。
N的常用对数简记作lgN.常用的两种对数:(2)自然对数:以无理数e=2.71828……
为底的对数叫自然对数(naturallogarithm),
为了简便,N的自然对数简记作lnN。积、商、幂的对数运算法则 对数换底公式 两个推论: 对数函数y=log a x (a>0, a≠1)(4) 0 x>1时, y>0(4) 00;
x>1时, y<0 (3) 过点(1,0), 即x=1 时, y=0 (1) 定义域: (0,+∞)(2) 值域:Rxyo(1, 0)xyo(1, 0)(5)在(0,+∞)上是减函数(5) 在(0,+∞)上是增函数对数函数的图象和性质
反函数的概念 一.幂函数的定义 一般地,函数 叫做幂函数
(power fun_ction),其中x是自变量, 是常数.几点说明:1) 中 前面系数是1,并且后面也没有常数项;2)要确定一个幂函数,需要一个条件就可以,即把常数
确定下来; 3)幂函数和指数函数的异同:两者都具有幂的形式,但
指数函数的自变量位于指数上,幂函数的自变量是底数.二.幂函数的图象及性质在同一平面直角坐标系内作出 , , , ,
, 的图像观察上述图象,将你发现的结论写在P78的表格内二.幂函数的图象及性质二.幂函数的图象及性质幂函数性质:1)所有的幂函数在(0,+∞)都有定义,并且图象都过点(1,1); 2)当α >0时,幂函数的图象都通过原点,并且
在[0,+∞)上是增函数
(从左往右看,函数图象逐渐上升)
当α<0时,幂函数在区间(0,+∞)上是减函数.
(从左往右看,函数图象逐渐上升)3)当α为奇数时,幂函数为奇函数,
当α为偶数时,幂函数为偶函数如图,幂函数
在第一象限对应的图像分别是C1, C2 , C3 , C4 , C5 ,则 大小如何排列?
一般地,函数y=ax(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R2.指数函数的图象和性质(见下表)曲线C1,C2,C3,C4 分别是指数函数y=ax,y=bx,y=cx,y=dx,和的图象,则a,b,c,d与1的大小关系是 b
3.可知y=f(x)+a的图象可由y=f(x) 得到,a>0时,向 (上,下)平移,a<0时,向 (上,下)平移。 一、对数的定义: 一般地,如果 的b次幂等于N, 即 (叫指数式), 那么数 b叫做 a为底N的对数 记作 (叫对数式),a叫做对数的底数, N叫做真数 三.几个常用结论:(1)负数与零没有对数 (1)常用对数:通常将以10为底的对数
叫做常用对数(common logarithm)。
N的常用对数简记作lgN.常用的两种对数:(2)自然对数:以无理数e=2.71828……
为底的对数叫自然对数(naturallogarithm),
为了简便,N的自然对数简记作lnN。积、商、幂的对数运算法则 对数换底公式 两个推论: 对数函数y=log a x (a>0, a≠1)(4) 0
x>1时, y<0 (3) 过点(1,0), 即x=1 时, y=0 (1) 定义域: (0,+∞)(2) 值域:Rxyo(1, 0)xyo(1, 0)(5)在(0,+∞)上是减函数(5) 在(0,+∞)上是增函数对数函数的图象和性质
反函数的概念 一.幂函数的定义 一般地,函数 叫做幂函数
(power fun_ction),其中x是自变量, 是常数.几点说明:1) 中 前面系数是1,并且后面也没有常数项;2)要确定一个幂函数,需要一个条件就可以,即把常数
确定下来; 3)幂函数和指数函数的异同:两者都具有幂的形式,但
指数函数的自变量位于指数上,幂函数的自变量是底数.二.幂函数的图象及性质在同一平面直角坐标系内作出 , , , ,
, 的图像观察上述图象,将你发现的结论写在P78的表格内二.幂函数的图象及性质二.幂函数的图象及性质幂函数性质:1)所有的幂函数在(0,+∞)都有定义,并且图象都过点(1,1); 2)当α >0时,幂函数的图象都通过原点,并且
在[0,+∞)上是增函数
(从左往右看,函数图象逐渐上升)
当α<0时,幂函数在区间(0,+∞)上是减函数.
(从左往右看,函数图象逐渐上升)3)当α为奇数时,幂函数为奇函数,
当α为偶数时,幂函数为偶函数如图,幂函数
在第一象限对应的图像分别是C1, C2 , C3 , C4 , C5 ,则 大小如何排列?
