22021-2022学年华东师大版八年级数学上册13.2.3边角边课件(共15张PPT)
文档属性
| 名称 | 22021-2022学年华东师大版八年级数学上册13.2.3边角边课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 171.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-18 08:41:50 | ||
图片预览


文档简介
(共15张PPT)
3.边角边(SAS)
13.2 三角形全等的判定
第2课时
华东师大版(八)上册
第13章 全等三角形
如果两个三角形有三组对应相等的元素(边或角),那么会有哪几种可能的情况?这时,这两个三角形一定会全等吗?
上节课我们讨论了以下问题:
有以下的四种情况:
知识回顾:
①. 两边一角、②.两角一边、
③.三角、 ④.三边.
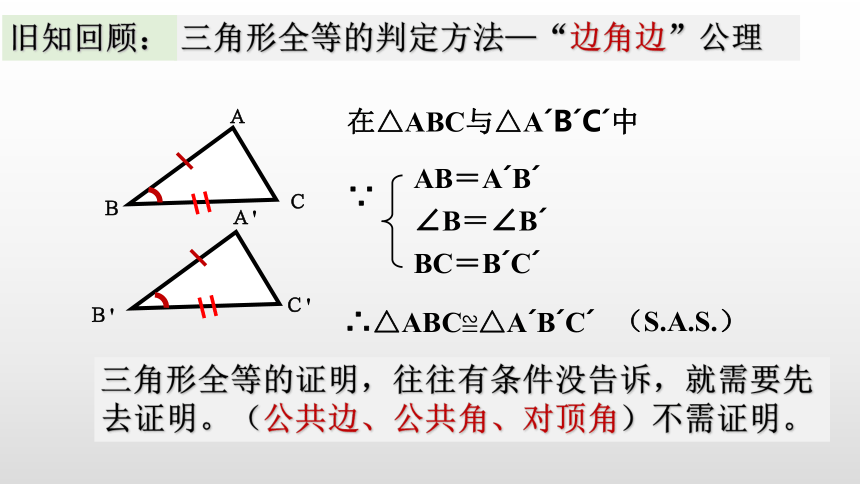
三角形全等的判定方法—“边角边”公理
A'
B'
C'
A
B
C
旧知回顾:
∴△ABC≌△AˊBˊCˊ
在△ABC与△AˊBˊCˊ中
AB=AˊBˊ
∠B=∠Bˊ
(S.A.S.)
∵
BC=BˊCˊ
三角形全等的证明,往往有条件没告诉,就需要先去证明。(公共边、公共角、对顶角)不需证明。
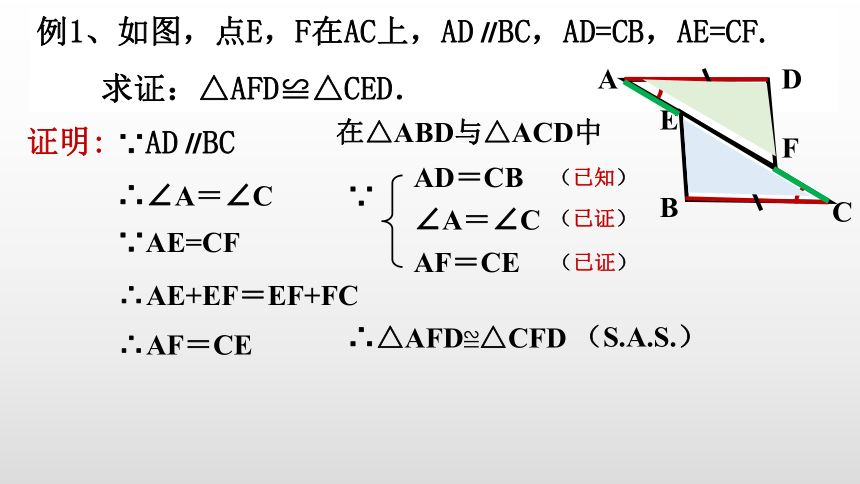
例1、如图,点E,F在AC上,AD∥BC,AD=CB,AE=CF.
求证:△AFD≌△CED.
证明:
∴∠A=∠C
∴AE+EF=EF+FC
∴△AFD≌△CFD
∵AD∥BC
在△ABD与△ACD中
AD=CB
∠A=∠C
∵AE=CF
(S.A.S.)
(已知)
(已证)
(已证)
A
B
C
D
F
E
∴AF=CE
∵
AF=CE
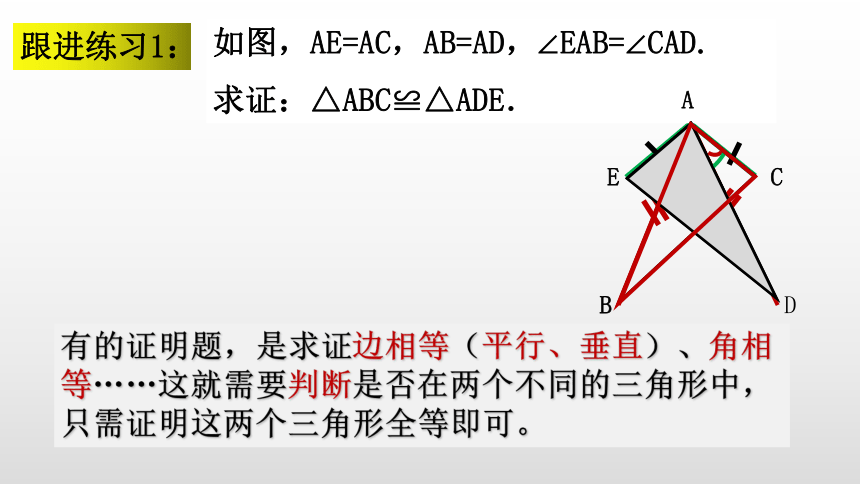
跟进练习1:
如图,AE=AC,AB=AD,∠EAB=∠CAD.
求证:△ABC≌△ADE.
A
B
C
E
D
有的证明题,是求证边相等(平行、垂直)、角相等……这就需要判断是否在两个不同的三角形中,只需证明这两个三角形全等即可。
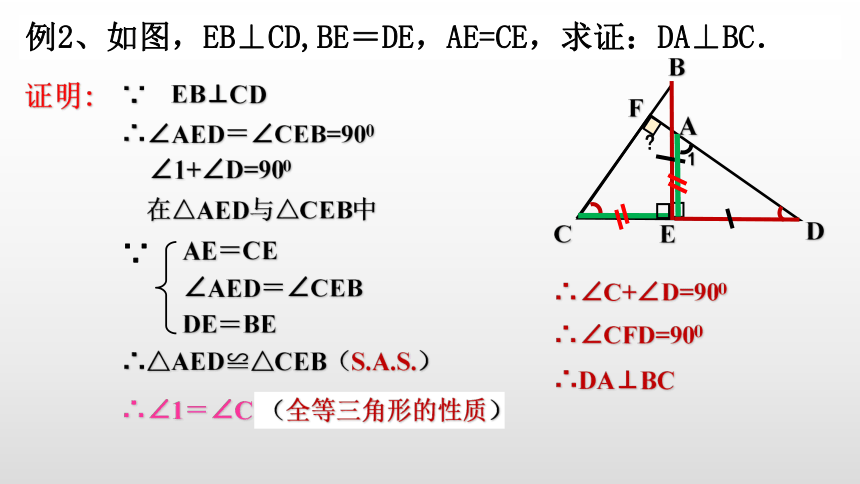
例2、如图,EB⊥CD,BE=DE,AE=CE,求证:DA⊥BC.
证明:
∵
∴∠AED=∠CEB=900
DE=BE
∴△AED≌△CEB(S.A.S.)
∵ EB⊥CD
在△AED与△CEB中
AE=CE
∠AED=∠CEB
∴∠1=∠C
(全等三角形的性质)
C
D
E
B
F
A
1
∠1+∠D=900
∴∠C+∠D=900
∴∠CFD=900
∴DA⊥BC
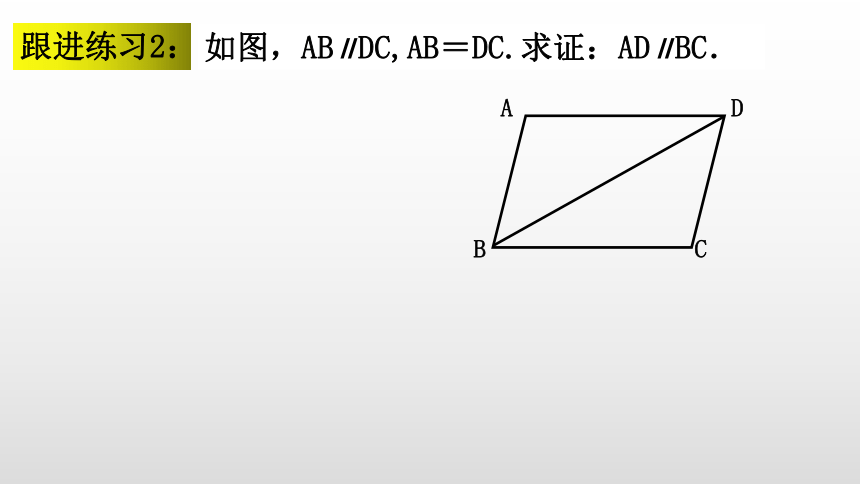
跟进练习2:
如图,AB∥DC,AB=DC.求证:AD∥BC.
A
B
C
D
如图,点B,E,F,D在同一条直线上,AB=CD,∠B=∠D,BF=DE.
求证:(1).AE=CF;(2).∠AFE=∠CEF
跟进练习3:
A
B
C
D
E
F
例3、如图,在正方形ABCD中,点P、Q是边CD和AD上的点,连结BP,BQ,PQ。∠PBQ=450.求证:PQ=AQ+CP.
A
B
C
D
P
Q
H
∟
∟
450
1
2
∟
3
证明:
∵在正方形ABCD中,
∠ABC=∠BAD=∠BCD=900
AB=BC
延长DA到H,使AH=CP
∴∠BAH=∠BCD=900
在 BAH和 BCP中,
∵
AB=BC
∠BAH=∠BCD
AH=CP
∴ BAH≌ BCP
∴∠3=∠2,
BH=BP
∵∠PBQ=450
∴∠1+∠2=450
(S.A.S.)
∴∠HBQ=∠PBQ
∴∠2+∠3=450
在 HBQ和 PBQ中,
∵ BH=BP
∠HBQ=∠PBQ
BP=BP
∴ HBQ≌ PBQ(S.A.S.)
∴HQ=PQ
∵HQ=AH+AQ
∴PQ=AQ+CP
A
B
C
D
P
Q
H
跟进练习4:
如图,CA⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想:线段CE与DE的关系,并说明理由。
A
E
B
D
C
跟进练习5:
如图, ABC和 都是等腰直角三角形,点A、C、D在同一条直线上,连结BD、AB,并延长AE角BD于点F。试判断:直线AE与BD的位置关系,并说明理由。
A
B
C
D
F
E
例4、如图,已知A、B、C三点在同一条直线上,分别以AB、BC为边在AC的同侧作等边 ABD和 BCE,连结AE交BD于点F,DC交BE于点G。求证:AE=DC.
A
B
C
E
D
F
G
3
1
2
证明:
∵ ABD和 BCE都是等边三角形
∴AB=DB,
BE=BC,
∠1=∠2
∴∠1+∠3=∠2+∠3
∴∠ABE=∠DBC
在 ABE和 DBC中,
∵
AB=DB
∠ABE=∠DBC
BE=BC
∴ ABD ≌ BCE(S.A.S.)
∴AE-DC
跟进练习6:
如图, ABD、 ACE和 ECF都是正三角形。求证:BE=DC=AF.
D
B
F
C
E
A
3.边角边(SAS)
13.2 三角形全等的判定
第2课时
华东师大版(八)上册
第13章 全等三角形
如果两个三角形有三组对应相等的元素(边或角),那么会有哪几种可能的情况?这时,这两个三角形一定会全等吗?
上节课我们讨论了以下问题:
有以下的四种情况:
知识回顾:
①. 两边一角、②.两角一边、
③.三角、 ④.三边.
三角形全等的判定方法—“边角边”公理
A'
B'
C'
A
B
C
旧知回顾:
∴△ABC≌△AˊBˊCˊ
在△ABC与△AˊBˊCˊ中
AB=AˊBˊ
∠B=∠Bˊ
(S.A.S.)
∵
BC=BˊCˊ
三角形全等的证明,往往有条件没告诉,就需要先去证明。(公共边、公共角、对顶角)不需证明。
例1、如图,点E,F在AC上,AD∥BC,AD=CB,AE=CF.
求证:△AFD≌△CED.
证明:
∴∠A=∠C
∴AE+EF=EF+FC
∴△AFD≌△CFD
∵AD∥BC
在△ABD与△ACD中
AD=CB
∠A=∠C
∵AE=CF
(S.A.S.)
(已知)
(已证)
(已证)
A
B
C
D
F
E
∴AF=CE
∵
AF=CE
跟进练习1:
如图,AE=AC,AB=AD,∠EAB=∠CAD.
求证:△ABC≌△ADE.
A
B
C
E
D
有的证明题,是求证边相等(平行、垂直)、角相等……这就需要判断是否在两个不同的三角形中,只需证明这两个三角形全等即可。
例2、如图,EB⊥CD,BE=DE,AE=CE,求证:DA⊥BC.
证明:
∵
∴∠AED=∠CEB=900
DE=BE
∴△AED≌△CEB(S.A.S.)
∵ EB⊥CD
在△AED与△CEB中
AE=CE
∠AED=∠CEB
∴∠1=∠C
(全等三角形的性质)
C
D
E
B
F
A
1
∠1+∠D=900
∴∠C+∠D=900
∴∠CFD=900
∴DA⊥BC
跟进练习2:
如图,AB∥DC,AB=DC.求证:AD∥BC.
A
B
C
D
如图,点B,E,F,D在同一条直线上,AB=CD,∠B=∠D,BF=DE.
求证:(1).AE=CF;(2).∠AFE=∠CEF
跟进练习3:
A
B
C
D
E
F
例3、如图,在正方形ABCD中,点P、Q是边CD和AD上的点,连结BP,BQ,PQ。∠PBQ=450.求证:PQ=AQ+CP.
A
B
C
D
P
Q
H
∟
∟
450
1
2
∟
3
证明:
∵在正方形ABCD中,
∠ABC=∠BAD=∠BCD=900
AB=BC
延长DA到H,使AH=CP
∴∠BAH=∠BCD=900
在 BAH和 BCP中,
∵
AB=BC
∠BAH=∠BCD
AH=CP
∴ BAH≌ BCP
∴∠3=∠2,
BH=BP
∵∠PBQ=450
∴∠1+∠2=450
(S.A.S.)
∴∠HBQ=∠PBQ
∴∠2+∠3=450
在 HBQ和 PBQ中,
∵ BH=BP
∠HBQ=∠PBQ
BP=BP
∴ HBQ≌ PBQ(S.A.S.)
∴HQ=PQ
∵HQ=AH+AQ
∴PQ=AQ+CP
A
B
C
D
P
Q
H
跟进练习4:
如图,CA⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想:线段CE与DE的关系,并说明理由。
A
E
B
D
C
跟进练习5:
如图, ABC和 都是等腰直角三角形,点A、C、D在同一条直线上,连结BD、AB,并延长AE角BD于点F。试判断:直线AE与BD的位置关系,并说明理由。
A
B
C
D
F
E
例4、如图,已知A、B、C三点在同一条直线上,分别以AB、BC为边在AC的同侧作等边 ABD和 BCE,连结AE交BD于点F,DC交BE于点G。求证:AE=DC.
A
B
C
E
D
F
G
3
1
2
证明:
∵ ABD和 BCE都是等边三角形
∴AB=DB,
BE=BC,
∠1=∠2
∴∠1+∠3=∠2+∠3
∴∠ABE=∠DBC
在 ABE和 DBC中,
∵
AB=DB
∠ABE=∠DBC
BE=BC
∴ ABD ≌ BCE(S.A.S.)
∴AE-DC
跟进练习6:
如图, ABD、 ACE和 ECF都是正三角形。求证:BE=DC=AF.
D
B
F
C
E
A
