2021-2022学年北师大版数学七年级下册2.3平行线的性质课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年北师大版数学七年级下册2.3平行线的性质课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1014.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-18 08:46:36 | ||
图片预览




文档简介
(共18张PPT)
温故知新
两直线平行
1、同位角相等
2、内错角相等
3、同旁内角互补
平行线的判定方法:
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
根据右图,填空:
①如果∠1=∠C,
那么__∥_( )
② 如果∠1=∠3
那么__∥_( )
③ 如果∠2+∠3=180°,
那么__∥__( )
AB
CD
EC
BD
同位角相等,两直线平行
内错角相等,两直线平行
AB
CD
同旁内角互补,两直线平行
角的关系
线的关系
条件是____ 、结论是____
A
B
C
E
D
1
2
3
思考:
条件和结论反过来,成立吗?
1. 掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补.
2. 能够根据平行线的性质进行简单的推理.
素养目标
3. 区分平行线的性质和判定的关系,培养学生逆向思维的能力.
(1).用直尺和三角尺画出两条平行线
a∥b,再画一条截线c,使之与直
线 a,b相交,并标出一对同位角.
(2).测量上面该对同位角的大小,记
录下来.从中你能发现什么
动手画一画、量一量、比一比
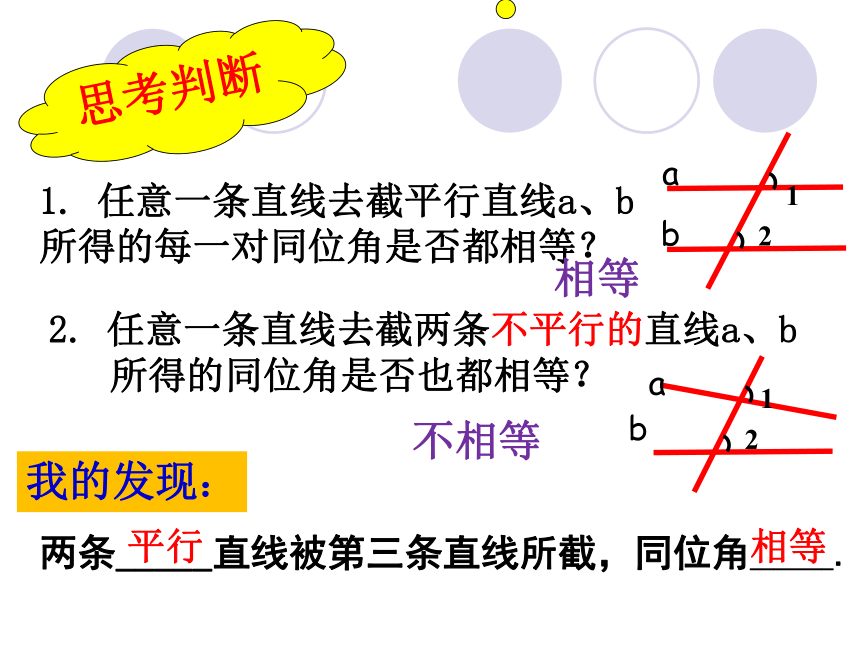
1. 任意一条直线去截平行直线a、b
所得的每一对同位角是否都相等?
思考判断
2. 任意一条直线去截两条不平行的直线a、b
所得的同位角是否也都相等?
我的发现:
两条_____直线被第三条直线所截,同位角_______.
平行
相等
b
1
2
a
b
1
2
a
相等
不相等
平行线的性质 1
结论
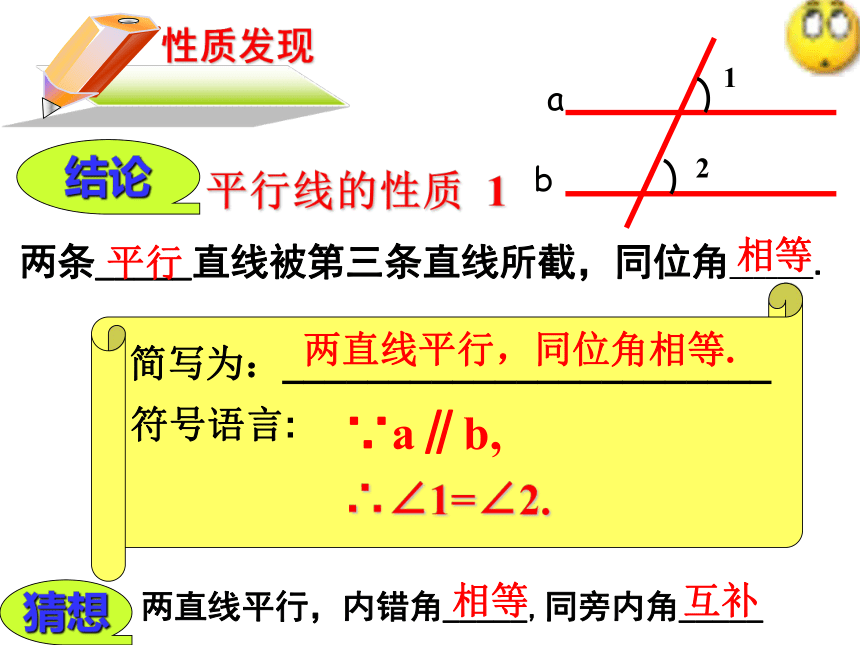
两条_____直线被第三条直线所截,同位角_______.
性质发现
∴∠1=∠2.
∵a∥b,
简写为:_______________________
符号语言:
b
1
2
a
平行
相等
两直线平行,同位角相等.
:两直线平行,内错角_____,同旁内角_____
相等
互补
猜想
1
2
3
a
b
思考
回答
如图,已知:a// b
那么 3与 2有什么数量关系?
平行线的性质 2
两条平行直线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等.
例如如右图因为 a∥b,
所以 ∠1= ∠2( ),
又 ∠3 = ___(对顶角相等),
所以∠ 2 = ∠3.
两直线平行,同位角相等
∠1
c
2
3
1
b
a
如图:已知a//b,那么 2与 3有什么数量关系呢?
平行线的性质 3
两条平行直线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补.
解: a//b (已知)
1= 2(两直线平行,同位角相等)
1+ 3=180°(补角定义)
2+ 3=180°(等量代换)
快速口答:当a∥b时 ,∠1 与∠2数量有什么关系 依据?
a
b
1
2
a
b
1
2
b
a
1
2
(1) (2) (3)
(1) 1+ 2=180°
两直线平行,同旁内角互补.
(2) 1= 2
两直线平行,内错角相等.
(3) 1= 2
两直线平行,同位角相等.
平行线的性质:
由 ______ ,定_____
线的关系
角的关系
◆ 课堂基础训练 ◆
选择题
1.如图,直线l与直线a,b相交,且a∥b ,∠1=50°,则∠2的度数是 ( )
A.130° B.50° C.100° D.120°
2.如图,直线a,b被直线c所截,若a∥b ,则下列不正确的是 ( )
A.∠1=∠2 B.∠2=∠4
C.∠1=∠4 D.∠1=∠5
B
D
3 下列说法:
①两条直线平行,同旁内角互补;
②同位角相等,两直线平行;
③内错角相等,两直线平行;
④垂直于同一直线的两直线平行,其中是平行线 的性质的是( )
A.① B.②和③ C.④ D.①和④
A
50°
两直线平行,同位角相等.
50°
两直线平行,内错角相等.
130°
两直线平行,同旁内角互补.
变式:已知∠3 =∠4,∠1=47°,求∠2的度数?
∴∠ 2= 47°( )
解:∵ ∠3 =∠4( )
∴a∥b( )
又∵∠ 1 = 47° ( )
c
1
2
3
4
a
b
d
做一做
如图,一束平行光线AB与DE射向一个水
平镜面后被反射,此时∠1=∠2,∠3=∠4.
(1)∠1与∠3的大小有什么关系?
∠2与∠4呢?
(2)反射光线BC与EF也平行吗?
梳理知识,颗粒归仓
两直线平行
同位角相等
内错角相等
同旁内角互补
2.线的关系
角的关系
判定
性质
平行线的性质和平行线的判定方法的
区 别 与 联 系
课堂小结我能行
1.平行线的性质
平行线的性质:
由“____”定“____”
由“____”定“____”
3.平行线的判定:
线
角
角
线
( )
( )
完成课本51页 习题1,2.
布置作业,强化理解
温故知新
两直线平行
1、同位角相等
2、内错角相等
3、同旁内角互补
平行线的判定方法:
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
根据右图,填空:
①如果∠1=∠C,
那么__∥_( )
② 如果∠1=∠3
那么__∥_( )
③ 如果∠2+∠3=180°,
那么__∥__( )
AB
CD
EC
BD
同位角相等,两直线平行
内错角相等,两直线平行
AB
CD
同旁内角互补,两直线平行
角的关系
线的关系
条件是____ 、结论是____
A
B
C
E
D
1
2
3
思考:
条件和结论反过来,成立吗?
1. 掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补.
2. 能够根据平行线的性质进行简单的推理.
素养目标
3. 区分平行线的性质和判定的关系,培养学生逆向思维的能力.
(1).用直尺和三角尺画出两条平行线
a∥b,再画一条截线c,使之与直
线 a,b相交,并标出一对同位角.
(2).测量上面该对同位角的大小,记
录下来.从中你能发现什么
动手画一画、量一量、比一比
1. 任意一条直线去截平行直线a、b
所得的每一对同位角是否都相等?
思考判断
2. 任意一条直线去截两条不平行的直线a、b
所得的同位角是否也都相等?
我的发现:
两条_____直线被第三条直线所截,同位角_______.
平行
相等
b
1
2
a
b
1
2
a
相等
不相等
平行线的性质 1
结论
两条_____直线被第三条直线所截,同位角_______.
性质发现
∴∠1=∠2.
∵a∥b,
简写为:_______________________
符号语言:
b
1
2
a
平行
相等
两直线平行,同位角相等.
:两直线平行,内错角_____,同旁内角_____
相等
互补
猜想
1
2
3
a
b
思考
回答
如图,已知:a// b
那么 3与 2有什么数量关系?
平行线的性质 2
两条平行直线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等.
例如如右图因为 a∥b,
所以 ∠1= ∠2( ),
又 ∠3 = ___(对顶角相等),
所以∠ 2 = ∠3.
两直线平行,同位角相等
∠1
c
2
3
1
b
a
如图:已知a//b,那么 2与 3有什么数量关系呢?
平行线的性质 3
两条平行直线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补.
解: a//b (已知)
1= 2(两直线平行,同位角相等)
1+ 3=180°(补角定义)
2+ 3=180°(等量代换)
快速口答:当a∥b时 ,∠1 与∠2数量有什么关系 依据?
a
b
1
2
a
b
1
2
b
a
1
2
(1) (2) (3)
(1) 1+ 2=180°
两直线平行,同旁内角互补.
(2) 1= 2
两直线平行,内错角相等.
(3) 1= 2
两直线平行,同位角相等.
平行线的性质:
由 ______ ,定_____
线的关系
角的关系
◆ 课堂基础训练 ◆
选择题
1.如图,直线l与直线a,b相交,且a∥b ,∠1=50°,则∠2的度数是 ( )
A.130° B.50° C.100° D.120°
2.如图,直线a,b被直线c所截,若a∥b ,则下列不正确的是 ( )
A.∠1=∠2 B.∠2=∠4
C.∠1=∠4 D.∠1=∠5
B
D
3 下列说法:
①两条直线平行,同旁内角互补;
②同位角相等,两直线平行;
③内错角相等,两直线平行;
④垂直于同一直线的两直线平行,其中是平行线 的性质的是( )
A.① B.②和③ C.④ D.①和④
A
50°
两直线平行,同位角相等.
50°
两直线平行,内错角相等.
130°
两直线平行,同旁内角互补.
变式:已知∠3 =∠4,∠1=47°,求∠2的度数?
∴∠ 2= 47°( )
解:∵ ∠3 =∠4( )
∴a∥b( )
又∵∠ 1 = 47° ( )
c
1
2
3
4
a
b
d
做一做
如图,一束平行光线AB与DE射向一个水
平镜面后被反射,此时∠1=∠2,∠3=∠4.
(1)∠1与∠3的大小有什么关系?
∠2与∠4呢?
(2)反射光线BC与EF也平行吗?
梳理知识,颗粒归仓
两直线平行
同位角相等
内错角相等
同旁内角互补
2.线的关系
角的关系
判定
性质
平行线的性质和平行线的判定方法的
区 别 与 联 系
课堂小结我能行
1.平行线的性质
平行线的性质:
由“____”定“____”
由“____”定“____”
3.平行线的判定:
线
角
角
线
( )
( )
完成课本51页 习题1,2.
布置作业,强化理解
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
