2021-2022学年华东师大版数学八年级上册第13章运动中的“三角板”问题课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年华东师大版数学八年级上册第13章运动中的“三角板”问题课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 421.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-18 08:51:56 | ||
图片预览






文档简介
(共20张PPT)
运动中的“三角板”问题
专题之一 —— 旋转(全等)
一、感受美
玩转风车
一、感受美
1、下列图形可看作是由什么变换得来的?
2、旋转前后两个图形存在什么关系?
二、探索美
探索:等腰直角三角板绕直角顶点旋转的
过程中还涉及那些数学问题或规律。
1、顺时针旋转30度
二、探索美
探索:等腰直角三角板绕直角顶点旋转的
过程中还涉及那些数学问题或规律。
2、顺时针旋转60度
二、探索美
探索:等腰直角三角板绕直角顶点旋转的
过程中还涉及那些数学问题或规律。
3、顺时针旋转270度
二、探索美
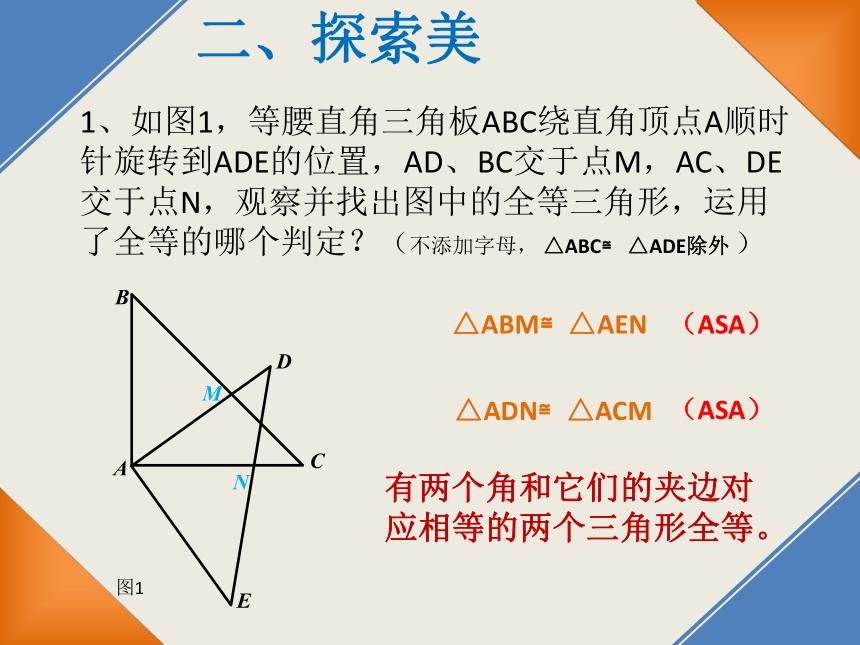
1、如图1,等腰直角三角板ABC绕直角顶点A顺时针旋转到ADE的位置,AD、BC交于点M,AC、DE交于点N,观察并找出图中的全等三角形,运用了全等的哪个判定?(不添加字母, △ABC≌ △ADE除外 )
图1
△ABM≌△AEN
△ADN≌△ACM
(ASA)
有两个角和它们的夹边对应相等的两个三角形全等。
(ASA)
A
B
C
D
E
M
N
二、探索美
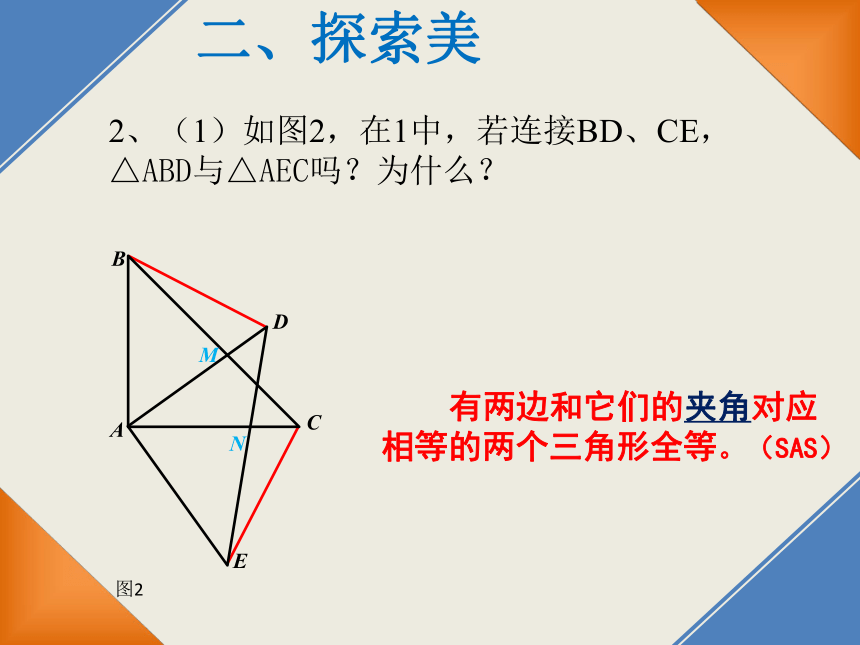
2、(1)如图2,在1中,若连接BD、CE,
△ABD与△AEC吗?为什么?
图2
有两边和它们的夹角对应相等的两个三角形全等。(SAS)
A
B
C
D
E
M
N
二、探索美
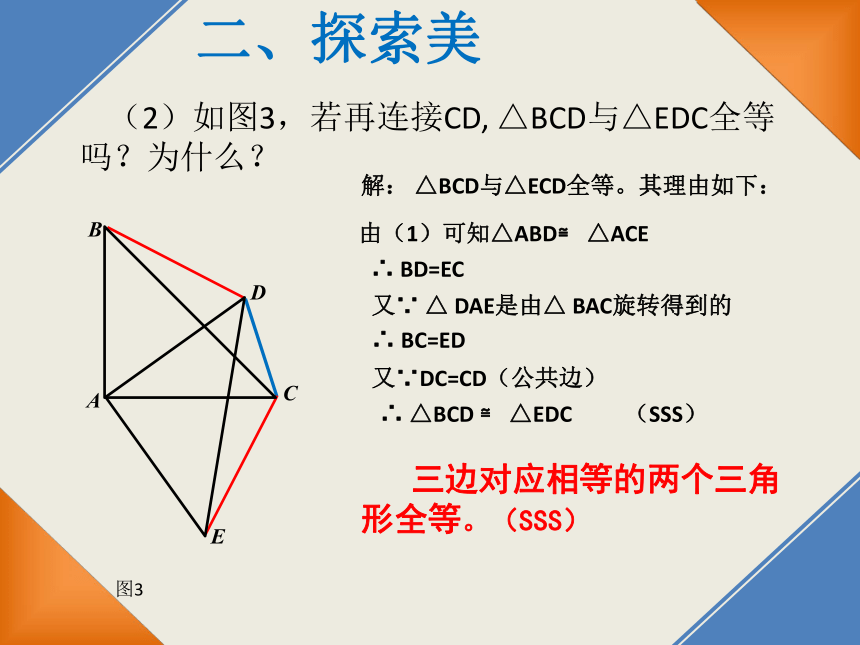
(2)如图3,若再连接CD, △BCD与△EDC全等吗?为什么?
三边对应相等的两个三角形全等。(SSS)
又∵DC=CD(公共边)
解: △BCD与△ECD全等。其理由如下:
由(1)可知△ABD≌ △ACE
∴ BD=EC
又∵ △ DAE是由△ BAC旋转得到的
∴ BC=ED
∴ △BCD ≌ △EDC
(SSS)
图3
A
B
C
D
E
三、鉴赏美
如图4,若等腰直角三角板绕直角顶点A顺时针继续旋转到如图所示的位置,△ABD与△ACE是否仍然全等?说明理由。
解: △ABD与△ACE全等。理由如下:
∵∠BAC=∠DAE=90°
∴∠BAC+∠CAD=∠DAE+∠CAD
即∠BAD=∠CAE
又∵AB=AC,AD=AE
∴ △ABD ≌△ACE
(SAS)
图4
A
B
C
D
E
四、创造美
如图5,若直角三角板DEF的直角顶点绕另一等腰直角三角板ABC的斜边中点旋转到如图所示位置AB、DE交于点N,AC、DF交于点M。
1、求证:BN=AM
证明两条线段相等最常见的方法是证明线段所在的两个三角形全等。
图5
A
B
C
D
E
F
M
N
四、创造美
2、如图6,连接MN,
求证:BN2 +CM2 =MN2
(课后思考)
图6
A
B
C
D
E
F
M
N
H
四、创造美
3、在图6中,若AB=AC=4,
求点A到NM的最大距离。
(课后思考)
图7
A
B
C
D
E
F
N
M
4.如图,A,O,D三点共线,△OAB和△OCD是两个全等的等边三角形,求∠AEB的大小.
C
B
O
D
A
E
解:
∵△OAB和△OCD是两个全等的等边三角形,
∴AO=BO,CO=DO, ∠AOB=∠COD=60°.
∵ A,O,D三点共线,
∴ ∠DOB=∠COA=120°,
∴ △COA ≌△DOB(S.A.S.).
∴ ∠DBO=∠CAO.
设OB与EA相交于点F,
∵ ∠EFB=∠AFO,
∴ ∠AEB=∠AOB=60°.
F
A
C
B
D
5. 如图,是西安半坡博物馆屋顶的截面图,已经知道它的两边AB和AC是相等的.建筑工人师傅对这个建筑物做出了两个判断:
①工人师傅在测量了∠B为37°以后,并没有测量∠C ,就说∠C 的度数也是37°;②工人师傅要加固屋顶,他们通过测量找到了横梁BC的中点D,然后在AD两点之间钉上一根木桩,他们认为木桩是垂直横梁的.
请同学们想想,工人师傅的说法对吗?请说明理由.
工人师傅的说法是对的,△ABC是等腰三角形,根据等腰三角形的性质可以得出这样的结论.
五、总结美
图7
6.证全等三角形的思路
1.小明想设计一种方案,测一下沼泽地的宽度AB的长度,如图所示,他在AB的垂线BM上分别取出C,D两点,使CD=BC,再过D点作出BM的垂线DN,并在DN上找一点E,使A,C,E三点共线,这时所测得DE的长就是这块沼泽地的宽AB的长度,你能说明理由吗?
解:在△ABC和△EDC中,
∠ABC=∠EDC=90°,∠ACB=∠ECD,
BC=DC,根据“A.S.A.”的判定定理可以判定△ABC≌△EDC,再由全等三角形的对应边相等,
可得AB=DE.
课后训练
课后训练
2.如图,在△ABC中,AC=BC, ∠ACB=90°,点D是AC上的一点,AE垂直BD的延长线于点E,且AE= BD.
求证:BD平分∠ABC.
A
B
D
E
)
)
1
2
C
3.如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边三角形CDE,使点E、A在直线DC的同侧,连结AE.求证:△DBC≌△EAC.
证明:∵△ABC和△EDC是等边三角形,
∴∠BCA=DCE=60°,
∴∠BCA-∠ACD=∠DCE-∠ACD,
即∠BCD=∠ACE.
在△DBC和△EAC中,
BC=AC,∠BCD=∠ACE,DC=EC,
∴△DBC≌△EAC.
课后训练
运动中的“三角板”问题
专题之一 —— 旋转(全等)
一、感受美
玩转风车
一、感受美
1、下列图形可看作是由什么变换得来的?
2、旋转前后两个图形存在什么关系?
二、探索美
探索:等腰直角三角板绕直角顶点旋转的
过程中还涉及那些数学问题或规律。
1、顺时针旋转30度
二、探索美
探索:等腰直角三角板绕直角顶点旋转的
过程中还涉及那些数学问题或规律。
2、顺时针旋转60度
二、探索美
探索:等腰直角三角板绕直角顶点旋转的
过程中还涉及那些数学问题或规律。
3、顺时针旋转270度
二、探索美
1、如图1,等腰直角三角板ABC绕直角顶点A顺时针旋转到ADE的位置,AD、BC交于点M,AC、DE交于点N,观察并找出图中的全等三角形,运用了全等的哪个判定?(不添加字母, △ABC≌ △ADE除外 )
图1
△ABM≌△AEN
△ADN≌△ACM
(ASA)
有两个角和它们的夹边对应相等的两个三角形全等。
(ASA)
A
B
C
D
E
M
N
二、探索美
2、(1)如图2,在1中,若连接BD、CE,
△ABD与△AEC吗?为什么?
图2
有两边和它们的夹角对应相等的两个三角形全等。(SAS)
A
B
C
D
E
M
N
二、探索美
(2)如图3,若再连接CD, △BCD与△EDC全等吗?为什么?
三边对应相等的两个三角形全等。(SSS)
又∵DC=CD(公共边)
解: △BCD与△ECD全等。其理由如下:
由(1)可知△ABD≌ △ACE
∴ BD=EC
又∵ △ DAE是由△ BAC旋转得到的
∴ BC=ED
∴ △BCD ≌ △EDC
(SSS)
图3
A
B
C
D
E
三、鉴赏美
如图4,若等腰直角三角板绕直角顶点A顺时针继续旋转到如图所示的位置,△ABD与△ACE是否仍然全等?说明理由。
解: △ABD与△ACE全等。理由如下:
∵∠BAC=∠DAE=90°
∴∠BAC+∠CAD=∠DAE+∠CAD
即∠BAD=∠CAE
又∵AB=AC,AD=AE
∴ △ABD ≌△ACE
(SAS)
图4
A
B
C
D
E
四、创造美
如图5,若直角三角板DEF的直角顶点绕另一等腰直角三角板ABC的斜边中点旋转到如图所示位置AB、DE交于点N,AC、DF交于点M。
1、求证:BN=AM
证明两条线段相等最常见的方法是证明线段所在的两个三角形全等。
图5
A
B
C
D
E
F
M
N
四、创造美
2、如图6,连接MN,
求证:BN2 +CM2 =MN2
(课后思考)
图6
A
B
C
D
E
F
M
N
H
四、创造美
3、在图6中,若AB=AC=4,
求点A到NM的最大距离。
(课后思考)
图7
A
B
C
D
E
F
N
M
4.如图,A,O,D三点共线,△OAB和△OCD是两个全等的等边三角形,求∠AEB的大小.
C
B
O
D
A
E
解:
∵△OAB和△OCD是两个全等的等边三角形,
∴AO=BO,CO=DO, ∠AOB=∠COD=60°.
∵ A,O,D三点共线,
∴ ∠DOB=∠COA=120°,
∴ △COA ≌△DOB(S.A.S.).
∴ ∠DBO=∠CAO.
设OB与EA相交于点F,
∵ ∠EFB=∠AFO,
∴ ∠AEB=∠AOB=60°.
F
A
C
B
D
5. 如图,是西安半坡博物馆屋顶的截面图,已经知道它的两边AB和AC是相等的.建筑工人师傅对这个建筑物做出了两个判断:
①工人师傅在测量了∠B为37°以后,并没有测量∠C ,就说∠C 的度数也是37°;②工人师傅要加固屋顶,他们通过测量找到了横梁BC的中点D,然后在AD两点之间钉上一根木桩,他们认为木桩是垂直横梁的.
请同学们想想,工人师傅的说法对吗?请说明理由.
工人师傅的说法是对的,△ABC是等腰三角形,根据等腰三角形的性质可以得出这样的结论.
五、总结美
图7
6.证全等三角形的思路
1.小明想设计一种方案,测一下沼泽地的宽度AB的长度,如图所示,他在AB的垂线BM上分别取出C,D两点,使CD=BC,再过D点作出BM的垂线DN,并在DN上找一点E,使A,C,E三点共线,这时所测得DE的长就是这块沼泽地的宽AB的长度,你能说明理由吗?
解:在△ABC和△EDC中,
∠ABC=∠EDC=90°,∠ACB=∠ECD,
BC=DC,根据“A.S.A.”的判定定理可以判定△ABC≌△EDC,再由全等三角形的对应边相等,
可得AB=DE.
课后训练
课后训练
2.如图,在△ABC中,AC=BC, ∠ACB=90°,点D是AC上的一点,AE垂直BD的延长线于点E,且AE= BD.
求证:BD平分∠ABC.
A
B
D
E
)
)
1
2
C
3.如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边三角形CDE,使点E、A在直线DC的同侧,连结AE.求证:△DBC≌△EAC.
证明:∵△ABC和△EDC是等边三角形,
∴∠BCA=DCE=60°,
∴∠BCA-∠ACD=∠DCE-∠ACD,
即∠BCD=∠ACE.
在△DBC和△EAC中,
BC=AC,∠BCD=∠ACE,DC=EC,
∴△DBC≌△EAC.
课后训练
