2021-2022学年北师大版九年级数学下册3.1圆 同步训练(word解析版)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.1圆 同步训练(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 175.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-19 00:00:00 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《3.1圆》同步达标训练(附答案)
1.下列说法中,不正确的是( )
A.圆既是轴对称图形又是中心对称图形 B.圆的每一条直径都是它的对称轴
C.圆有无数条对称轴 D.圆的对称中心是它的圆心
2.已知⊙O的半径是5cm,则⊙O中最长的弦长是( )
A.5cm B.10cm C.15cm D.20cm
3.下列说法正确的是( )
A.直径是弦,弦是直径 B.圆有无数条对称轴
C.无论过圆内哪一点,都只能作一条直径 D.度数相等的弧是等弧
4.已知AB是直径为10的圆的一条弦,则AB的长度不可能是( )
A.2 B.5 C.9 D.11
5.如图,一量角器放置在∠AOB上,角的一边OA与量角器交于点C、D,且点C处的度数是20°,点D处的度数为110°,则∠AOB的度数是( )
A.20° B.25° C.45° D.55°
6.到圆心的距离大于半径的点的集合是( )
A.圆的内部 B.圆的外部
C.圆 D.圆的外部和圆
7.如图,AB是⊙O的直径,点C、D在⊙O上,且点C、D在AB的异侧,连接AD、OD、OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
8.⊙O中,直径AB=a,弦CD=b,则a与b大小为( )
A.a>b B.a≥b C.a<b D.a≤b
9.已知⊙O的半径为6cm,P为线段OA的中点,若点P在⊙O上,则OA的长( )
A.等于6cm B.等于12cm C.小于6cm D.大于12cm
10.如图,⊙O的半径为6,△OAB的面积为18,点P为弦AB上一动点,当OP长为整数时,P点有 个.
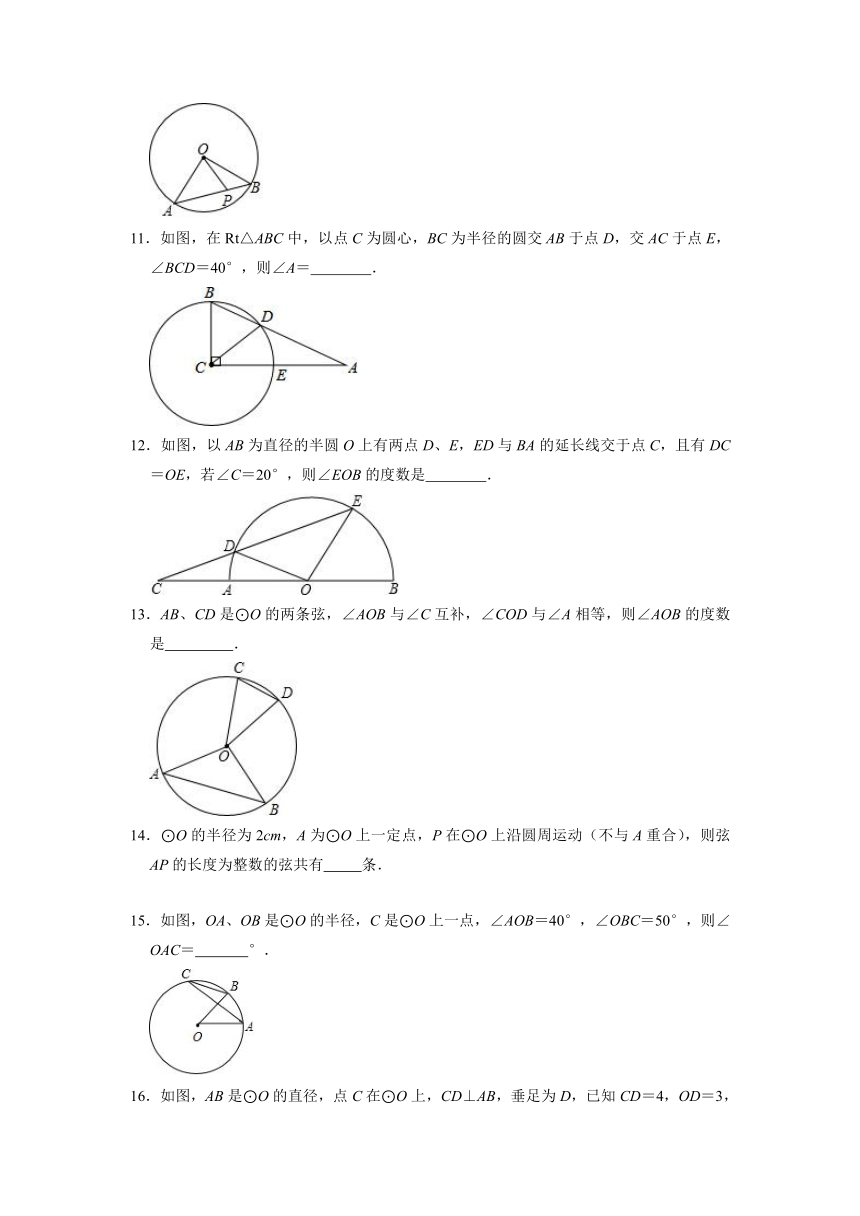
11.如图,在Rt△ABC中,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,∠BCD=40°,则∠A= .
12.如图,以AB为直径的半圆O上有两点D、E,ED与BA的延长线交于点C,且有DC=OE,若∠C=20°,则∠EOB的度数是 .
13.AB、CD是⊙O的两条弦,∠AOB与∠C互补,∠COD与∠A相等,则∠AOB的度数是 .
14.⊙O的半径为2cm,A为⊙O上一定点,P在⊙O上沿圆周运动(不与A重合),则弦AP的长度为整数的弦共有 条.
15.如图,OA、OB是⊙O的半径,C是⊙O上一点,∠AOB=40°,∠OBC=50°,则∠OAC= °.
16.如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,已知CD=4,OD=3,求AB的长是 .
17.如图,C是以点O为圆心,AB为直径的半圆上一点,且CO⊥AB,在OC两侧分别作矩形OGHI和正方形ODEF,且点I,F在OC上,点H,E在半圆上,可证:IG=FD.小云发现连接图中已知点得到两条线段,便可证明IG=FD.
请回答:小云所作的两条线段分别是 和 ;
证明IG=FD的依据是矩形的对角线相等, 和等量代换.
18.如图,点A、B、C是⊙O上的三点,BO平分∠ABC.求证:BA=BC.
19.已知:如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
20.如图,大半圆中有n个小半圆,大半圆弧长为L1,n个小半圆的弧长和为L2,找出L1和L2的关系并证明你的结论.(友情提示:利用弧长公式)
21.如图:A、B、C是⊙O上的三点,∠AOB=50°,∠OBC=40°,求∠OAC的度数.
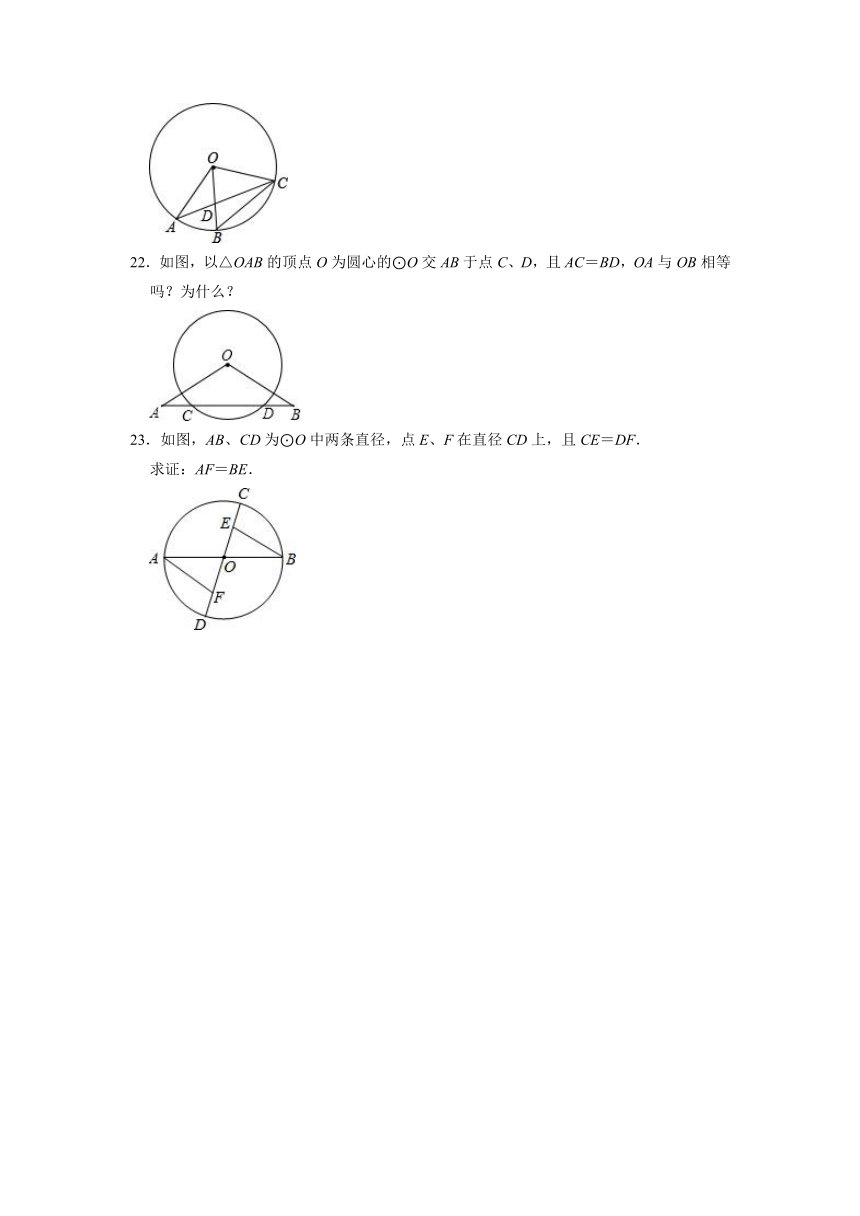
22.如图,以△OAB的顶点O为圆心的⊙O交AB于点C、D,且AC=BD,OA与OB相等吗?为什么?
23.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
参考答案
1.解:A.圆既是轴对称图形又是中心对称图形,正确;
B.圆的每一条直径所在直线都是它的对称轴,故B错误;
C.圆有无数条对称轴,正确;
D.圆的对称中心是它的圆心,正确.
故选:B.
2.解:∵⊙O的半径是5cm,
∴⊙O中最长的弦,即直径的长为10cm,
故选:B.
3.解:A、直径是弦,但弦不一定是直径,故错误,不符合题意;
B、圆有无数条直径,故正确,符合题意;
C、过圆心有无数条直径,故错误,不符合题意;
D、完全重合的弧是等弧,故错误,不符合题意;
故选:B.
4.解:因为圆中最长的弦为直径,
所以弦长L≤10.
故选:D.
5.解:连接CE、ED
∵角的一边OA与量角器交于点C、D,且点C处的度数是20°,点D处的度数为110°,即∠4=20°,∠OED=110°
∴∠3=∠OED﹣∠4=110°﹣20°=90°.
∴∠1=∠2=45°,∠5=∠2+∠3=45°+90°=135°
故∠AOB=180°﹣∠5﹣∠4=180°﹣135°﹣20°=25°
故选:B.
6.解:根据点和圆的位置关系,知圆的外部是到圆心的距离大于的所有点的集合;
故选:B.
7.解:∵AD∥OC,
∴∠AOC=∠DAO=70°,
又∵OD=OA,
∴∠ADO=∠DAO=70°,
∴∠AOD=180﹣70°﹣70°=40°.
故选:D.
8.解:直径是圆中最长的弦,因而有a≥b.
故选:B.
9.解:根据点和圆的位置关系,得OP=6,再根据线段的中点的概念,得OA=2OP=12.
故选:B.
10.解:解法一:过O作OC⊥AB于C,则AC=BC,
设OC=x,AC=y,
∵AB是⊙O的一条弦,⊙O的半径为6,
∴AB≤12,
∵△OAB的面积为18,
∴,
则y=,
∴,
解得x=3或﹣3(舍),
∴OC=3>4,
∴4<OP≤6,
∵点P为弦AB上一动点,当OP长为整数时,OP=5或6,P点有4个.
解法二:设△AOB中OA边上的高为h,
则,即,
∴h=6,
∵OB=6,
∴OA⊥OB,即∠AOB=90°,
∴AB=6,图中OC=3,
同理得:点P为弦AB上一动点,当OP长为整数时,OP=5或6,P点有4个.
故答案为:4.
11.解:∵CB=CD,
∴∠B=∠CDB,
∵∠B+∠CDB+∠BCD=180°,
∴∠B=(180°﹣∠BCD)=(180°﹣40°)=70°,
∵∠ACB=90°,
∴∠A=90°﹣∠B=20°.
故答案为20°.
12.解:∵CD=OD=OE,
∴∠C=∠DOC=20°,
∴∠EDO=∠E=40°,
∴∠EOB=∠C+∠E=20°+40°=60°.
故答案为:60°.
13.解:设∠AOB=x,则∠C=∠D=180°﹣x,
∴∠COD=180°﹣2∠C=2x﹣180°,
∴∠A=∠B=(180°﹣x),
∵∠COD=∠A,
∴2x﹣180°=(180°﹣x),
解得x=108°.
故答案为:108°.
14.解:如图,
∵⊙O的直径AB=4,
∴弦长的整数值有1,2,3,4四种可能,
这样的弦共有7条,
故答案为7.
15.解:连接OC,
∵OC=OB,
∴∠OCB=∠OBC=50°,
∴∠BOC=180°﹣50°×2=80°,
∴∠AOC=80°+40°=120°,
∵OC=OA,
∴∠OAC=∠OCA=30°,
故答案为:30.
16.解:连接OC,
∵CD=4,OD=3,
在Rt△ODC中,
∴OC===5,
∴AB=2OC=10,
故答案为:10.
17.解:连接OH、OE,如图所示:
∵在矩形OGHI和正方形ODEF中,IG=OH,OE=FD,
∵OH=OE,
∴IG=FD;
故答案为:OH、OE,同圆的半径相等.
18.证明:连OA、OC,如图,
∵OA=OB,OB=OC,
∴∠ABO=∠BAO,∠CBO=∠BCO,
∵BO平分∠ABC,
∴∠ABO=∠CBO,
∴∠BAO=∠BCO,
∴△OAB≌△OCB,
∴AB=BC.
19.解:AC与BD相等.理由如下:
连接OC、OD,如图,
∵OA=OB,AE=BF,
∴OE=OF,
∵CE⊥AB,DF⊥AB,
∴∠OEC=∠OFD=90°,
在Rt△OEC和Rt△OFD中,
,
∴Rt△OEC≌Rt△OFD(HL),
∴∠COE=∠DOF,
∴=,
∴AC=BD.
20.解:L1=L2.理由如下:
设n个小半圆半径依次为r1,r2,…,rn.
则大圆半径为(r1+r2+…+rn)
∴L1=π(r1+r2+…+rn),
L2=πr1+πr2+…+πrn
=π(r1+r2+…+rn),
∴L1=L2.
21.解:∵OB=OC∴∠OCB=∠OBC=40°(2分)
∴∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣40°﹣40°=100°(3分)
∴∠AOC=∠AOB+∠BOC=50°+100°=150°(4分)
又∵OA=OC∴∠OAC==15°(6分)
22.答:OA=OB.
理由如下:
如图,过O作OE⊥AB于E,
∵CD是⊙O的弦,OE⊥CD,
∴CE=DE,
∵AC=BD,
∴AE=BE,
∵OE⊥CD,
∴OA=OB.
23.解:∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
1.下列说法中,不正确的是( )
A.圆既是轴对称图形又是中心对称图形 B.圆的每一条直径都是它的对称轴
C.圆有无数条对称轴 D.圆的对称中心是它的圆心
2.已知⊙O的半径是5cm,则⊙O中最长的弦长是( )
A.5cm B.10cm C.15cm D.20cm
3.下列说法正确的是( )
A.直径是弦,弦是直径 B.圆有无数条对称轴
C.无论过圆内哪一点,都只能作一条直径 D.度数相等的弧是等弧
4.已知AB是直径为10的圆的一条弦,则AB的长度不可能是( )
A.2 B.5 C.9 D.11
5.如图,一量角器放置在∠AOB上,角的一边OA与量角器交于点C、D,且点C处的度数是20°,点D处的度数为110°,则∠AOB的度数是( )
A.20° B.25° C.45° D.55°
6.到圆心的距离大于半径的点的集合是( )
A.圆的内部 B.圆的外部
C.圆 D.圆的外部和圆
7.如图,AB是⊙O的直径,点C、D在⊙O上,且点C、D在AB的异侧,连接AD、OD、OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
8.⊙O中,直径AB=a,弦CD=b,则a与b大小为( )
A.a>b B.a≥b C.a<b D.a≤b
9.已知⊙O的半径为6cm,P为线段OA的中点,若点P在⊙O上,则OA的长( )
A.等于6cm B.等于12cm C.小于6cm D.大于12cm
10.如图,⊙O的半径为6,△OAB的面积为18,点P为弦AB上一动点,当OP长为整数时,P点有 个.
11.如图,在Rt△ABC中,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,∠BCD=40°,则∠A= .
12.如图,以AB为直径的半圆O上有两点D、E,ED与BA的延长线交于点C,且有DC=OE,若∠C=20°,则∠EOB的度数是 .
13.AB、CD是⊙O的两条弦,∠AOB与∠C互补,∠COD与∠A相等,则∠AOB的度数是 .
14.⊙O的半径为2cm,A为⊙O上一定点,P在⊙O上沿圆周运动(不与A重合),则弦AP的长度为整数的弦共有 条.
15.如图,OA、OB是⊙O的半径,C是⊙O上一点,∠AOB=40°,∠OBC=50°,则∠OAC= °.
16.如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,已知CD=4,OD=3,求AB的长是 .
17.如图,C是以点O为圆心,AB为直径的半圆上一点,且CO⊥AB,在OC两侧分别作矩形OGHI和正方形ODEF,且点I,F在OC上,点H,E在半圆上,可证:IG=FD.小云发现连接图中已知点得到两条线段,便可证明IG=FD.
请回答:小云所作的两条线段分别是 和 ;
证明IG=FD的依据是矩形的对角线相等, 和等量代换.
18.如图,点A、B、C是⊙O上的三点,BO平分∠ABC.求证:BA=BC.
19.已知:如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
20.如图,大半圆中有n个小半圆,大半圆弧长为L1,n个小半圆的弧长和为L2,找出L1和L2的关系并证明你的结论.(友情提示:利用弧长公式)
21.如图:A、B、C是⊙O上的三点,∠AOB=50°,∠OBC=40°,求∠OAC的度数.
22.如图,以△OAB的顶点O为圆心的⊙O交AB于点C、D,且AC=BD,OA与OB相等吗?为什么?
23.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
参考答案
1.解:A.圆既是轴对称图形又是中心对称图形,正确;
B.圆的每一条直径所在直线都是它的对称轴,故B错误;
C.圆有无数条对称轴,正确;
D.圆的对称中心是它的圆心,正确.
故选:B.
2.解:∵⊙O的半径是5cm,
∴⊙O中最长的弦,即直径的长为10cm,
故选:B.
3.解:A、直径是弦,但弦不一定是直径,故错误,不符合题意;
B、圆有无数条直径,故正确,符合题意;
C、过圆心有无数条直径,故错误,不符合题意;
D、完全重合的弧是等弧,故错误,不符合题意;
故选:B.
4.解:因为圆中最长的弦为直径,
所以弦长L≤10.
故选:D.
5.解:连接CE、ED
∵角的一边OA与量角器交于点C、D,且点C处的度数是20°,点D处的度数为110°,即∠4=20°,∠OED=110°
∴∠3=∠OED﹣∠4=110°﹣20°=90°.
∴∠1=∠2=45°,∠5=∠2+∠3=45°+90°=135°
故∠AOB=180°﹣∠5﹣∠4=180°﹣135°﹣20°=25°
故选:B.
6.解:根据点和圆的位置关系,知圆的外部是到圆心的距离大于的所有点的集合;
故选:B.
7.解:∵AD∥OC,
∴∠AOC=∠DAO=70°,
又∵OD=OA,
∴∠ADO=∠DAO=70°,
∴∠AOD=180﹣70°﹣70°=40°.
故选:D.
8.解:直径是圆中最长的弦,因而有a≥b.
故选:B.
9.解:根据点和圆的位置关系,得OP=6,再根据线段的中点的概念,得OA=2OP=12.
故选:B.
10.解:解法一:过O作OC⊥AB于C,则AC=BC,
设OC=x,AC=y,
∵AB是⊙O的一条弦,⊙O的半径为6,
∴AB≤12,
∵△OAB的面积为18,
∴,
则y=,
∴,
解得x=3或﹣3(舍),
∴OC=3>4,
∴4<OP≤6,
∵点P为弦AB上一动点,当OP长为整数时,OP=5或6,P点有4个.
解法二:设△AOB中OA边上的高为h,
则,即,
∴h=6,
∵OB=6,
∴OA⊥OB,即∠AOB=90°,
∴AB=6,图中OC=3,
同理得:点P为弦AB上一动点,当OP长为整数时,OP=5或6,P点有4个.
故答案为:4.
11.解:∵CB=CD,
∴∠B=∠CDB,
∵∠B+∠CDB+∠BCD=180°,
∴∠B=(180°﹣∠BCD)=(180°﹣40°)=70°,
∵∠ACB=90°,
∴∠A=90°﹣∠B=20°.
故答案为20°.
12.解:∵CD=OD=OE,
∴∠C=∠DOC=20°,
∴∠EDO=∠E=40°,
∴∠EOB=∠C+∠E=20°+40°=60°.
故答案为:60°.
13.解:设∠AOB=x,则∠C=∠D=180°﹣x,
∴∠COD=180°﹣2∠C=2x﹣180°,
∴∠A=∠B=(180°﹣x),
∵∠COD=∠A,
∴2x﹣180°=(180°﹣x),
解得x=108°.
故答案为:108°.
14.解:如图,
∵⊙O的直径AB=4,
∴弦长的整数值有1,2,3,4四种可能,
这样的弦共有7条,
故答案为7.
15.解:连接OC,
∵OC=OB,
∴∠OCB=∠OBC=50°,
∴∠BOC=180°﹣50°×2=80°,
∴∠AOC=80°+40°=120°,
∵OC=OA,
∴∠OAC=∠OCA=30°,
故答案为:30.
16.解:连接OC,
∵CD=4,OD=3,
在Rt△ODC中,
∴OC===5,
∴AB=2OC=10,
故答案为:10.
17.解:连接OH、OE,如图所示:
∵在矩形OGHI和正方形ODEF中,IG=OH,OE=FD,
∵OH=OE,
∴IG=FD;
故答案为:OH、OE,同圆的半径相等.
18.证明:连OA、OC,如图,
∵OA=OB,OB=OC,
∴∠ABO=∠BAO,∠CBO=∠BCO,
∵BO平分∠ABC,
∴∠ABO=∠CBO,
∴∠BAO=∠BCO,
∴△OAB≌△OCB,
∴AB=BC.
19.解:AC与BD相等.理由如下:
连接OC、OD,如图,
∵OA=OB,AE=BF,
∴OE=OF,
∵CE⊥AB,DF⊥AB,
∴∠OEC=∠OFD=90°,
在Rt△OEC和Rt△OFD中,
,
∴Rt△OEC≌Rt△OFD(HL),
∴∠COE=∠DOF,
∴=,
∴AC=BD.
20.解:L1=L2.理由如下:
设n个小半圆半径依次为r1,r2,…,rn.
则大圆半径为(r1+r2+…+rn)
∴L1=π(r1+r2+…+rn),
L2=πr1+πr2+…+πrn
=π(r1+r2+…+rn),
∴L1=L2.
21.解:∵OB=OC∴∠OCB=∠OBC=40°(2分)
∴∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣40°﹣40°=100°(3分)
∴∠AOC=∠AOB+∠BOC=50°+100°=150°(4分)
又∵OA=OC∴∠OAC==15°(6分)
22.答:OA=OB.
理由如下:
如图,过O作OE⊥AB于E,
∵CD是⊙O的弦,OE⊥CD,
∴CE=DE,
∵AC=BD,
∴AE=BE,
∵OE⊥CD,
∴OA=OB.
23.解:∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
