2021-2022学年青岛版九年级数学上册第二章解直角三角形巩固复习练习(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年青岛版九年级数学上册第二章解直角三角形巩固复习练习(Word版,附答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 234.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-19 22:40:02 | ||
图片预览




文档简介
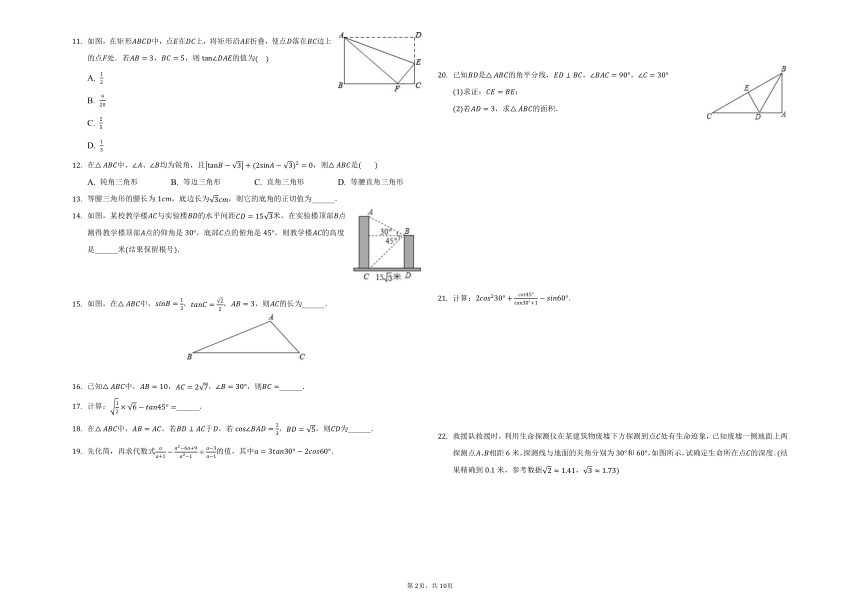
第二章《解直角三角形》巩固复习练习
如图,在的正方形网格中,每个小正方形的边长都是,的顶点都在这些小正方形的顶点上,那么的值为
A.
B.
C.
D.
已知,则锐角的取值范围是
A. B. C. D.
如图,中,,,于点,是线段上的一个动点,则的最小值是
A.
B.
C.
D.
如图,在处测得点在北偏东方向上,在处测得点在北偏东方向上,若米,则点到直线距离为
A. 米
B. 米
C. 米
D. 米
如图,在中,,若,,则的值是
A.
B.
C.
D.
某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆的长为
A. 米
B. 米
C. 米
D. 米
如图,在中,是斜边上的高,,则下列比值中不等于的是
A.
B.
C.
D.
如图,港口在观测站的正东方向,,某船从港口出发,沿北偏东方向航行一段距离后到达处,此时从观测站处测得该船位于北偏东的方向,则该船与观测站之间的距离即的长为
A.
B.
C.
D.
如图,中,,点在上,若,,则的长度为
A.
B.
C.
D.
从一艘船上测得海岸上高为米的灯塔顶部的仰角为时,船离灯塔的水平距离是
A. 米 B. 米 C. 米 D. 米
如图,在矩形中,点在上,将矩形沿折叠,使点落在边上的点处.若,,则的值为
A.
B.
C.
D.
在中,、均为锐角,且,则是
A. 钝角三角形 B. 等边三角形 C. 直角三角形 D. 等腰直角三角形
等腰三角形的腰长为,底边长为,则它的底角的正切值为______.
如图,某校教学楼与实验楼的水平间距米,在实验楼顶部点测得教学楼顶部点的仰角是,底部点的俯角是,则教学楼的高度是______米结果保留根号.
如图,在中,,,,则的长为______.
已知中,,,,则______.
计算:______.
在中,,若于,若,,则为______.
先化简,再求代数式的值,其中.
已知是的角平分线,,,
求证:;
若,求的面积.
计算:.
救援队救援时,利用生命探测仪在某建筑物废墟下方探测到点处有生命迹象,已知废墟一侧地面上两探测点、相距米,探测线与地面的夹角分别为和,如图所示,试确定生命所在点的深度.结果精确到米,参考数据,
如图,在中,为锐角,,,,求的长.
在菱形中,对角线、相交于点,为的中点,连接并延长到点,使,连接,.
求证:四边形是矩形;
若,,求的长.
南海诸岛自古以来都是中国的领土,月日,中央军委在南海海域隆重举行海上阅兵,军委主席习近平登上长沙舰检阅海军舰艇编队,包括辽宁号航母在内的艘舰艇参加了阅兵仪式.如图,、是两处海港,其中在东偏南方向千米处,辽宁号航母从海港出发,沿东偏北方向,以千米小时的速度匀速航行,两小时后,长沙舰从海港出发,沿东偏北的方向匀速航行,两舰恰好同时到达阅兵地点.
长沙舰从海港出发航行到达阅兵地点用了多少时间?
求长沙舰的航行速度.结果保留根号
答案和解析
1.【答案】
【解析】解:如图,过点作于.
在中,,,
,
,
故选:.
如图,过点作于利用勾股定理求出即可解决问题.
本题考查锐角三角函数的定义,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
2.【答案】
【解析】解:,,
,
,
故选:.
根据余弦值随着角度的增大或减小而减小或增大;
本题考查了锐角三角函数的增减性,关键是熟练掌握当角度在间变化时,
正弦值随着角度的增大或减小而增大或减小;
余弦值随着角度的增大或减小而减小或增大;
正切值随着角度的增大或减小而增大或减小.
3.【答案】
【解析】
【分析】
本题考查解直角三角形,等腰三角形的性质,垂线段最短等知识,解题的关键是学会添加常用辅助线,用转化的思想思考问题,属于中考常考题型.
作于,于由,设,,利用勾股定理构建方程求出,再证明,推出,由垂线段最短即可解决问题.
【解答】
解:如图,作于,于.
,
,
,设,,
则有:,
,
或舍弃,
,
,,,
等腰三角形两腰上的高相等
,,
,
,
,
,
,
的最小值为.
4.【答案】
【解析】解:设点到直线距离为米,
在中,,
在中,,
由题意得,,
解得,米,
故选:.
设点到直线距离为米,根据正切的定义用表示出、,根据题意列出方程,解方程即可.
本题考查的是解直角三角形的应用,掌握锐角三角函数的定义、正确标注方向角是解题的关键.
5.【答案】
【解析】解:由勾股定理得,,
,
故选:.
根据勾股定理求出,根据余弦的定义解答.
本题考查的是锐角三角函数的定义,掌握锐角的邻边与斜边的比叫做的余弦是解题的关键.
6.【答案】
【解析】解:作于点,
则,
,
,
解得,米,
故选:.
根据题意作出合适的辅助线,然后利用锐角三角函数即可表示出的长.
本题考查解直角三角形的应用、轴对称图形,解答本题的关键是明确题意,利用数形结合的思想解答.
7.【答案】
【解析】解:是斜边上的高,
,
,
,
,
,
,
故选:.
根据垂直定义证出,然后根据余弦定义可得答案.
此题主要考查了锐角函数定义,关键是掌握余弦邻边:斜边.
8.【答案】
【解析】解:如图,过点作于.
在中,,,,
,,
在中,,,
,
,
即该船与观测站之间的距离即的长为.
故选:.
过点作于先解,得出,,再由是等腰直角三角形,得出,于是得到结论.
本题考查了解直角三角形的应用方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键.
9.【答案】
【解析】解:,,,
,
,
.
,
,
故选:.
在中,由三角函数求得,再由勾股定理求得,最后在中由三角函数求得.
本题主要考查了勾股定理,解直角三角形的应用,关键是解直角三角形.
10.【答案】
【解析】解:根据题意可得:船离海岸线的距离为米
故选:.
在直角三角形中,已知角的对边求邻边,可以用正切函数来解决.
本题考查解直角三角形的应用仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.
11.【答案】
【解析】解:四边形为矩形,
,,
矩形沿直线折叠,顶点恰好落在边上的处,
,,
在中,,
,
设,则
在中,,
,解得,
,
,
故选:.
先根据矩形的性质得,,再根据折叠的性质得,,在中,利用勾股定理计算出,则,设,则,然后在中根据勾股定理得到,解方程即可得到,进一步得到的长,再根据余弦函数的定义即可求解.
本题考查了翻折变换,矩形的性质,解直角三角形,勾股定理,灵活运用这些性质进行推理是本题的关键.
12.【答案】
【解析】
【分析】
本题主要考查特殊角的锐角三角函数、非负数的性质和等边三角形的判定,牢记特殊角的锐角三角函数值是解决问题的关键根据非负数的性质和特殊角的锐角三角函数值求出和的度数,即可判定是什么三角形.
【解答】
解:,
,,
,,
是等边三角形.
故选B.
13.【答案】
【解析】解:设,,
过点作,垂足为,如图所示:
则,
在中,由勾股定理得:,
,
故答案为:.
作等腰三角形底边上的高,将问题转化到直角三角形中,求底角的正切值即可.
本题考查了等腰三角形的性质、勾股定理、三角函数定义等知识,熟练掌握等腰三角形的性质是解题的关键.
14.【答案】
【解析】
【分析】
本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.
首先分析图形:根据题意构造直角三角形.本题涉及到两个直角三角形、,进而可解即可求出答案.
【解答】
解:过点作于点,
在中,,,
可得米.
在中,,,
可得米.
故教学楼的高度是米.
答:教学楼的高度是米.
15.【答案】
【解析】
【分析】
此题考查了解直角三角形,涉及的知识有:锐角三角函数定义,以及勾股定理,熟练掌握各自的性质是解本题的关键.过作垂直于,在直角三角形中,利用锐角三角函数定义求出的长,在直角三角形中,利用锐角三角函数定义求出的长,再利用勾股定理求出的长即可.
【解答】
解:过作,
在中,,,
,
在中,,
,即,
根据勾股定理得:,
故答案为.
16.【答案】或
【解析】解:作交或延长线于点,
如图,当、位于异侧时,
在中,,,
,,
在中,,
,
则;
如图,当、在的同侧时,
由知,,,
则,
综上,或,
故答案为或.
作交或延长线于点,分、位于异侧和同侧两种情况,先在中求得、的值,再在中利用勾股定理求得的长,继而就两种情况分别求出的长.
本题主要考查解直角三角形,解题的关键是熟练掌握三角函数的运用、分类讨论思想的运算及勾股定理.
17.【答案】
【解析】解:,
故答案为:.
根据二次根式的乘法运算的法则和特殊角的三角函数值计算即可.
本题考查了二次根式的混合运算,特殊角的三角函数值,熟记法则是解题的关键.
18.【答案】或
【解析】解:如图,若为锐角三角形,
,
,
,
设,则,
,
,
解得:或舍,
,,
;
如图,若为钝角三角形,
由知,,,
,
故答案为:或.
分为锐角三角形和钝角三角形两种情况,在中由,可设设,则,结合的长根据勾股定理可得,求得的值后即可得,,在锐角三角形中,在钝角三角形中即可得答案.
本题考查了等腰三角形的性质,解直角三角形,勾股定理的应用,解此题的关键是根据三角形的形状分类讨论.
19.【答案】解:
,
当--时,原式.
【解析】根据分式的除法和减法可以化简题目中的式子,然后根据的值,即可解答本题.
本题考查分式的化简求值、特殊角的三角函数值,解答本题的关键是明确分式化简求值的方法.
20.【答案】证明:,,
,
平分,
,
,
,
,
.
解:在中,,,,
,,
,
,
的面积.
【解析】证明即可解决问题.
解直角三角形求出,即可解决问题.
本题考查解直角三角形的应用,等腰三角形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
21.【答案】解:原式,
,
.
【解析】此题主要考查了特殊角的三角函数值,实数的运算,涉及二次根式的运算,分母有理化等知识,关键是掌握、、角的各种三角函数值.
首先代入特殊角的三角函数值,然后再计算乘方,后算乘法,最后计算加减即可.
22.【答案】解:过点作,交的延长线于,
在中,,,
,
在中,,,
,
由题意得,,
,
解得,米,
答:生命所在点的深度约为米.
【解析】过点作,根据正切的定义分别用表示出、,根据题意列出方程,解方程得到答案.
本题考查的是解直角三角形的应用坡度坡角问题,掌握坡度坡角的概念、熟记锐角三角函数的定义是解题的关键.
23.【答案】解:作于点,
.
,,
.
在中,.
,
在中,.
.
【解析】作,在中求得、,再在中根据、求得,继而根据可得答案.
本题主要考查解直角三角形,解题的关键是根据题意构建合适的直角三角形及三角函数的定义.
24.【答案】解:证明:点为的中点,,
四边形是平行四边形,
又四边形是菱形,
,
,
四边形是矩形;
四边形是矩形,
,,
又四边形是菱形,
,
,
在中,,
,
,
.
【解析】根据有一个角是度的平行四边形是矩形即可证明四边形是矩形;
根据矩形和菱形的性质可得,,再根据锐角三角函数即可求出的长.
本题考查了菱形的性质、矩形的判定与性质、锐角三角函数定义,解决本题的关键是综合运用以上知识.
25.【答案】解:由题意得:,,,
,
过点作,垂足为,
在中,,
在中,,
,,
,
辽宁号航母从到的时间为小时,
则长沙舰从到所用时间为小时,
答:长沙舰从海港出发航行到达阅兵地点用了小时.
长沙舰的速度为千米小时,
答:长沙舰的航行速度为千米小时.
【解析】根据方位角可以得出的各个内角的度数,根据所给的条件,可以求出三条边的长,于是可以求出辽宁号舰从到的时间,进而求出长沙舰从到的时间,
根据路程除以时间就是速度,即求出的长度和长沙舰行驶所有时间.
考查方位角的意义和解直角三角形等知识,将方位角转化到三角形的内角是关键,正确的解直角三角形是前提.第2页,共2页
第1页,共3页
如图,在的正方形网格中,每个小正方形的边长都是,的顶点都在这些小正方形的顶点上,那么的值为
A.
B.
C.
D.
已知,则锐角的取值范围是
A. B. C. D.
如图,中,,,于点,是线段上的一个动点,则的最小值是
A.
B.
C.
D.
如图,在处测得点在北偏东方向上,在处测得点在北偏东方向上,若米,则点到直线距离为
A. 米
B. 米
C. 米
D. 米
如图,在中,,若,,则的值是
A.
B.
C.
D.
某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆的长为
A. 米
B. 米
C. 米
D. 米
如图,在中,是斜边上的高,,则下列比值中不等于的是
A.
B.
C.
D.
如图,港口在观测站的正东方向,,某船从港口出发,沿北偏东方向航行一段距离后到达处,此时从观测站处测得该船位于北偏东的方向,则该船与观测站之间的距离即的长为
A.
B.
C.
D.
如图,中,,点在上,若,,则的长度为
A.
B.
C.
D.
从一艘船上测得海岸上高为米的灯塔顶部的仰角为时,船离灯塔的水平距离是
A. 米 B. 米 C. 米 D. 米
如图,在矩形中,点在上,将矩形沿折叠,使点落在边上的点处.若,,则的值为
A.
B.
C.
D.
在中,、均为锐角,且,则是
A. 钝角三角形 B. 等边三角形 C. 直角三角形 D. 等腰直角三角形
等腰三角形的腰长为,底边长为,则它的底角的正切值为______.
如图,某校教学楼与实验楼的水平间距米,在实验楼顶部点测得教学楼顶部点的仰角是,底部点的俯角是,则教学楼的高度是______米结果保留根号.
如图,在中,,,,则的长为______.
已知中,,,,则______.
计算:______.
在中,,若于,若,,则为______.
先化简,再求代数式的值,其中.
已知是的角平分线,,,
求证:;
若,求的面积.
计算:.
救援队救援时,利用生命探测仪在某建筑物废墟下方探测到点处有生命迹象,已知废墟一侧地面上两探测点、相距米,探测线与地面的夹角分别为和,如图所示,试确定生命所在点的深度.结果精确到米,参考数据,
如图,在中,为锐角,,,,求的长.
在菱形中,对角线、相交于点,为的中点,连接并延长到点,使,连接,.
求证:四边形是矩形;
若,,求的长.
南海诸岛自古以来都是中国的领土,月日,中央军委在南海海域隆重举行海上阅兵,军委主席习近平登上长沙舰检阅海军舰艇编队,包括辽宁号航母在内的艘舰艇参加了阅兵仪式.如图,、是两处海港,其中在东偏南方向千米处,辽宁号航母从海港出发,沿东偏北方向,以千米小时的速度匀速航行,两小时后,长沙舰从海港出发,沿东偏北的方向匀速航行,两舰恰好同时到达阅兵地点.
长沙舰从海港出发航行到达阅兵地点用了多少时间?
求长沙舰的航行速度.结果保留根号
答案和解析
1.【答案】
【解析】解:如图,过点作于.
在中,,,
,
,
故选:.
如图,过点作于利用勾股定理求出即可解决问题.
本题考查锐角三角函数的定义,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
2.【答案】
【解析】解:,,
,
,
故选:.
根据余弦值随着角度的增大或减小而减小或增大;
本题考查了锐角三角函数的增减性,关键是熟练掌握当角度在间变化时,
正弦值随着角度的增大或减小而增大或减小;
余弦值随着角度的增大或减小而减小或增大;
正切值随着角度的增大或减小而增大或减小.
3.【答案】
【解析】
【分析】
本题考查解直角三角形,等腰三角形的性质,垂线段最短等知识,解题的关键是学会添加常用辅助线,用转化的思想思考问题,属于中考常考题型.
作于,于由,设,,利用勾股定理构建方程求出,再证明,推出,由垂线段最短即可解决问题.
【解答】
解:如图,作于,于.
,
,
,设,,
则有:,
,
或舍弃,
,
,,,
等腰三角形两腰上的高相等
,,
,
,
,
,
,
的最小值为.
4.【答案】
【解析】解:设点到直线距离为米,
在中,,
在中,,
由题意得,,
解得,米,
故选:.
设点到直线距离为米,根据正切的定义用表示出、,根据题意列出方程,解方程即可.
本题考查的是解直角三角形的应用,掌握锐角三角函数的定义、正确标注方向角是解题的关键.
5.【答案】
【解析】解:由勾股定理得,,
,
故选:.
根据勾股定理求出,根据余弦的定义解答.
本题考查的是锐角三角函数的定义,掌握锐角的邻边与斜边的比叫做的余弦是解题的关键.
6.【答案】
【解析】解:作于点,
则,
,
,
解得,米,
故选:.
根据题意作出合适的辅助线,然后利用锐角三角函数即可表示出的长.
本题考查解直角三角形的应用、轴对称图形,解答本题的关键是明确题意,利用数形结合的思想解答.
7.【答案】
【解析】解:是斜边上的高,
,
,
,
,
,
,
故选:.
根据垂直定义证出,然后根据余弦定义可得答案.
此题主要考查了锐角函数定义,关键是掌握余弦邻边:斜边.
8.【答案】
【解析】解:如图,过点作于.
在中,,,,
,,
在中,,,
,
,
即该船与观测站之间的距离即的长为.
故选:.
过点作于先解,得出,,再由是等腰直角三角形,得出,于是得到结论.
本题考查了解直角三角形的应用方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键.
9.【答案】
【解析】解:,,,
,
,
.
,
,
故选:.
在中,由三角函数求得,再由勾股定理求得,最后在中由三角函数求得.
本题主要考查了勾股定理,解直角三角形的应用,关键是解直角三角形.
10.【答案】
【解析】解:根据题意可得:船离海岸线的距离为米
故选:.
在直角三角形中,已知角的对边求邻边,可以用正切函数来解决.
本题考查解直角三角形的应用仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.
11.【答案】
【解析】解:四边形为矩形,
,,
矩形沿直线折叠,顶点恰好落在边上的处,
,,
在中,,
,
设,则
在中,,
,解得,
,
,
故选:.
先根据矩形的性质得,,再根据折叠的性质得,,在中,利用勾股定理计算出,则,设,则,然后在中根据勾股定理得到,解方程即可得到,进一步得到的长,再根据余弦函数的定义即可求解.
本题考查了翻折变换,矩形的性质,解直角三角形,勾股定理,灵活运用这些性质进行推理是本题的关键.
12.【答案】
【解析】
【分析】
本题主要考查特殊角的锐角三角函数、非负数的性质和等边三角形的判定,牢记特殊角的锐角三角函数值是解决问题的关键根据非负数的性质和特殊角的锐角三角函数值求出和的度数,即可判定是什么三角形.
【解答】
解:,
,,
,,
是等边三角形.
故选B.
13.【答案】
【解析】解:设,,
过点作,垂足为,如图所示:
则,
在中,由勾股定理得:,
,
故答案为:.
作等腰三角形底边上的高,将问题转化到直角三角形中,求底角的正切值即可.
本题考查了等腰三角形的性质、勾股定理、三角函数定义等知识,熟练掌握等腰三角形的性质是解题的关键.
14.【答案】
【解析】
【分析】
本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.
首先分析图形:根据题意构造直角三角形.本题涉及到两个直角三角形、,进而可解即可求出答案.
【解答】
解:过点作于点,
在中,,,
可得米.
在中,,,
可得米.
故教学楼的高度是米.
答:教学楼的高度是米.
15.【答案】
【解析】
【分析】
此题考查了解直角三角形,涉及的知识有:锐角三角函数定义,以及勾股定理,熟练掌握各自的性质是解本题的关键.过作垂直于,在直角三角形中,利用锐角三角函数定义求出的长,在直角三角形中,利用锐角三角函数定义求出的长,再利用勾股定理求出的长即可.
【解答】
解:过作,
在中,,,
,
在中,,
,即,
根据勾股定理得:,
故答案为.
16.【答案】或
【解析】解:作交或延长线于点,
如图,当、位于异侧时,
在中,,,
,,
在中,,
,
则;
如图,当、在的同侧时,
由知,,,
则,
综上,或,
故答案为或.
作交或延长线于点,分、位于异侧和同侧两种情况,先在中求得、的值,再在中利用勾股定理求得的长,继而就两种情况分别求出的长.
本题主要考查解直角三角形,解题的关键是熟练掌握三角函数的运用、分类讨论思想的运算及勾股定理.
17.【答案】
【解析】解:,
故答案为:.
根据二次根式的乘法运算的法则和特殊角的三角函数值计算即可.
本题考查了二次根式的混合运算,特殊角的三角函数值,熟记法则是解题的关键.
18.【答案】或
【解析】解:如图,若为锐角三角形,
,
,
,
设,则,
,
,
解得:或舍,
,,
;
如图,若为钝角三角形,
由知,,,
,
故答案为:或.
分为锐角三角形和钝角三角形两种情况,在中由,可设设,则,结合的长根据勾股定理可得,求得的值后即可得,,在锐角三角形中,在钝角三角形中即可得答案.
本题考查了等腰三角形的性质,解直角三角形,勾股定理的应用,解此题的关键是根据三角形的形状分类讨论.
19.【答案】解:
,
当--时,原式.
【解析】根据分式的除法和减法可以化简题目中的式子,然后根据的值,即可解答本题.
本题考查分式的化简求值、特殊角的三角函数值,解答本题的关键是明确分式化简求值的方法.
20.【答案】证明:,,
,
平分,
,
,
,
,
.
解:在中,,,,
,,
,
,
的面积.
【解析】证明即可解决问题.
解直角三角形求出,即可解决问题.
本题考查解直角三角形的应用,等腰三角形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
21.【答案】解:原式,
,
.
【解析】此题主要考查了特殊角的三角函数值,实数的运算,涉及二次根式的运算,分母有理化等知识,关键是掌握、、角的各种三角函数值.
首先代入特殊角的三角函数值,然后再计算乘方,后算乘法,最后计算加减即可.
22.【答案】解:过点作,交的延长线于,
在中,,,
,
在中,,,
,
由题意得,,
,
解得,米,
答:生命所在点的深度约为米.
【解析】过点作,根据正切的定义分别用表示出、,根据题意列出方程,解方程得到答案.
本题考查的是解直角三角形的应用坡度坡角问题,掌握坡度坡角的概念、熟记锐角三角函数的定义是解题的关键.
23.【答案】解:作于点,
.
,,
.
在中,.
,
在中,.
.
【解析】作,在中求得、,再在中根据、求得,继而根据可得答案.
本题主要考查解直角三角形,解题的关键是根据题意构建合适的直角三角形及三角函数的定义.
24.【答案】解:证明:点为的中点,,
四边形是平行四边形,
又四边形是菱形,
,
,
四边形是矩形;
四边形是矩形,
,,
又四边形是菱形,
,
,
在中,,
,
,
.
【解析】根据有一个角是度的平行四边形是矩形即可证明四边形是矩形;
根据矩形和菱形的性质可得,,再根据锐角三角函数即可求出的长.
本题考查了菱形的性质、矩形的判定与性质、锐角三角函数定义,解决本题的关键是综合运用以上知识.
25.【答案】解:由题意得:,,,
,
过点作,垂足为,
在中,,
在中,,
,,
,
辽宁号航母从到的时间为小时,
则长沙舰从到所用时间为小时,
答:长沙舰从海港出发航行到达阅兵地点用了小时.
长沙舰的速度为千米小时,
答:长沙舰的航行速度为千米小时.
【解析】根据方位角可以得出的各个内角的度数,根据所给的条件,可以求出三条边的长,于是可以求出辽宁号舰从到的时间,进而求出长沙舰从到的时间,
根据路程除以时间就是速度,即求出的长度和长沙舰行驶所有时间.
考查方位角的意义和解直角三角形等知识,将方位角转化到三角形的内角是关键,正确的解直角三角形是前提.第2页,共2页
第1页,共3页
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
