沪科版数学七年级上册 3.2 一元一次方程的应用课件(共15张PPT)
文档属性
| 名称 | 沪科版数学七年级上册 3.2 一元一次方程的应用课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 580.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-18 10:54:07 | ||
图片预览





文档简介
(共15张PPT)
3.2一元一次方程的应用(1)
----等积和行程问题
学习目标
1、会用一元一次方程解决关于几何图形 中等积变化问题和行程问题
2、掌握方程解应用题的一般步骤
3、能体会数学问题源于实际生活,会从实际情境中建立方程模型
自学指导
请同学们认真阅读P93-94练习上面的内容,思考以下问题:
1、对于例1中的你能用含未知数的代数式表示出钢材体积在锻造前后的体积?它们有什么关系?你会列出含有未知数的一元一次方程吗?
2、你还记得小学中的路程、速度和时间的关系吗?你能用它们的关系解决例2吗?。
3、列方程解应用题的一般步骤有哪些?
5分钟后,老师期待你的精彩展示
例1:
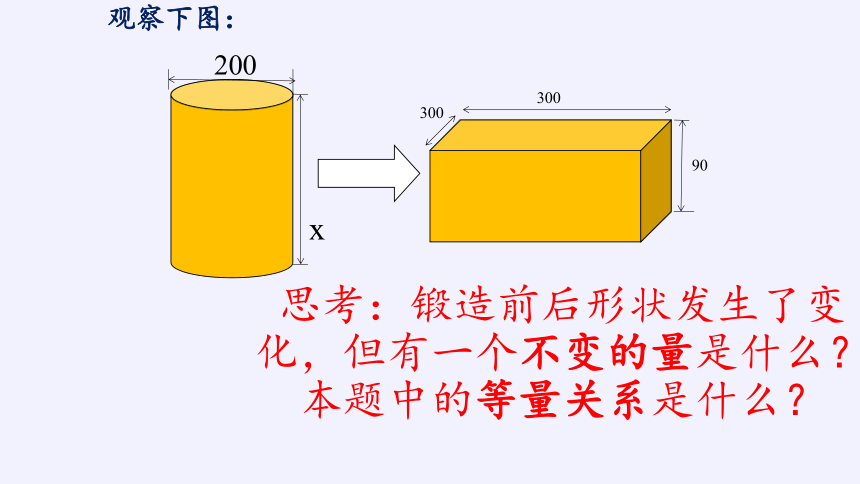
用直径为200mm的圆柱钢,锻造一个长、宽、高分别是300mm、300mm和90mm的长方体,至少应截取多少毫米的圆柱体钢(计算时π取3.14,结果精确到1mm)
合作探究
思考:锻造前后形状发生了变化,但有一个不变的量是什么?本题中的等量关系是什么?
观察下图:
x
200
90
300
300
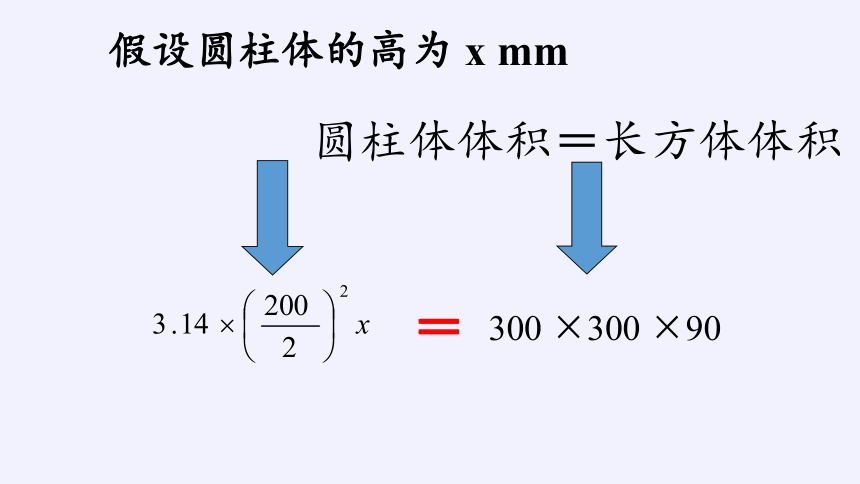
圆柱体体积=长方体体积
=
300 ×300 ×90
假设圆柱体的高为 x mm
解:设至少要截取圆柱体钢 mm.
根据题意得:
答:至少应截圆柱体钢长约是258mm.
解方程,得
总结:变形前的体积=变形后的体积
题目中的等量关系是什么?路程和平均速度、时间之间有什么关系?
提速前后路程相等
路程=平均速度x时间
如果设提速前的平均速度xkm/h,怎么表示提速后的速度?
你能列出方程吗?
提速后的平均速度为(x+40)km/h
解:由题意,
得
解方程,得
答:提速前这趟客车的平均速度是71km/h.
1、 把直径6cm,长16cm的圆钢锻造成半径为4cm的圆钢。求锻造后的圆钢的长。
当堂训练:
解:设锻造后的圆钢的长为x㎝
答:锻造后圆钢的长是9cm
2.甲、乙两地相距180km,一人骑自行车从甲地出发每小时行15km;另一人骑摩托车从乙地同时出发,两人相向而行,已知摩托车速度是自行车速度的3倍,问多少时间后两人相遇?
解:设x小时相遇,
60x=180
x=3
答:3小时后后两人相遇.
当堂训练:
小结:
通过例题的学习,你能总结列方程
解应用题的一般步骤吗?
审设
找
列
解
检、答
课堂作业:习题3.2 第2、3题
课外作业:课后练习1、2
完成同步练习3.2.1
作业:
谢 谢
3.2一元一次方程的应用(1)
----等积和行程问题
学习目标
1、会用一元一次方程解决关于几何图形 中等积变化问题和行程问题
2、掌握方程解应用题的一般步骤
3、能体会数学问题源于实际生活,会从实际情境中建立方程模型
自学指导
请同学们认真阅读P93-94练习上面的内容,思考以下问题:
1、对于例1中的你能用含未知数的代数式表示出钢材体积在锻造前后的体积?它们有什么关系?你会列出含有未知数的一元一次方程吗?
2、你还记得小学中的路程、速度和时间的关系吗?你能用它们的关系解决例2吗?。
3、列方程解应用题的一般步骤有哪些?
5分钟后,老师期待你的精彩展示
例1:
用直径为200mm的圆柱钢,锻造一个长、宽、高分别是300mm、300mm和90mm的长方体,至少应截取多少毫米的圆柱体钢(计算时π取3.14,结果精确到1mm)
合作探究
思考:锻造前后形状发生了变化,但有一个不变的量是什么?本题中的等量关系是什么?
观察下图:
x
200
90
300
300
圆柱体体积=长方体体积
=
300 ×300 ×90
假设圆柱体的高为 x mm
解:设至少要截取圆柱体钢 mm.
根据题意得:
答:至少应截圆柱体钢长约是258mm.
解方程,得
总结:变形前的体积=变形后的体积
题目中的等量关系是什么?路程和平均速度、时间之间有什么关系?
提速前后路程相等
路程=平均速度x时间
如果设提速前的平均速度xkm/h,怎么表示提速后的速度?
你能列出方程吗?
提速后的平均速度为(x+40)km/h
解:由题意,
得
解方程,得
答:提速前这趟客车的平均速度是71km/h.
1、 把直径6cm,长16cm的圆钢锻造成半径为4cm的圆钢。求锻造后的圆钢的长。
当堂训练:
解:设锻造后的圆钢的长为x㎝
答:锻造后圆钢的长是9cm
2.甲、乙两地相距180km,一人骑自行车从甲地出发每小时行15km;另一人骑摩托车从乙地同时出发,两人相向而行,已知摩托车速度是自行车速度的3倍,问多少时间后两人相遇?
解:设x小时相遇,
60x=180
x=3
答:3小时后后两人相遇.
当堂训练:
小结:
通过例题的学习,你能总结列方程
解应用题的一般步骤吗?
审设
找
列
解
检、答
课堂作业:习题3.2 第2、3题
课外作业:课后练习1、2
完成同步练习3.2.1
作业:
谢 谢
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
