沪科版数学七年级上册 3.5三元一次方程组及其解法 课件(共15张PPT)
文档属性
| 名称 | 沪科版数学七年级上册 3.5三元一次方程组及其解法 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 217.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-18 10:57:02 | ||
图片预览




文档简介
(共15张PPT)
三元一次方程组及其解法
《九章算术 》方程中第一题:
今有上禾三秉,中禾二秉,下禾一秉,实三十九斗;上禾二秉,中禾三秉,下禾一秉,实三十四斗;上禾一秉,中禾二秉,下禾三秉,实二十六斗。问上、中、下禾实一秉各几何?
解:设上、中、下等稻子(禾)每捆(秉)可出谷子(实)分别x、y、z(斗),可得
3x+2y+z=39
2x+3y+z=34
x+2y+3z=26
定义:由三个一次方程组成的含三个未知数的方程组,
叫三元一次方程组。
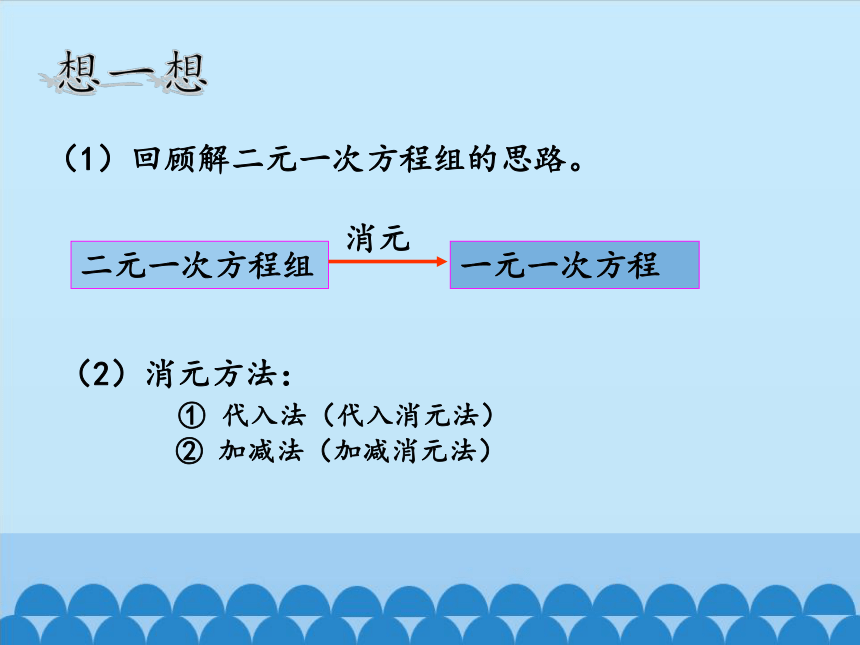
(1)回顾解二元一次方程组的思路。
想一想
二元一次方程组
一元一次方程
消元
(2)消元方法:
① 代入法(代入消元法)
② 加减法(加减消元法)
设1元、2元、5元的纸币分别为x张、y张、z张
根据题意,可以得到下面三个方程:
x+y+z=12
x+4y-z=15
x+2y+5z=22
①
②
③
观察方程你能得出什么?
都含有三个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做三元一次方程。
这个问题的解必须同时满足上面三个条件,因此,我们把这三个方程合在一起,写成
x+y+z=12
x+4y-z=15
x+2y+5z=22
{
这个方程组含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组。
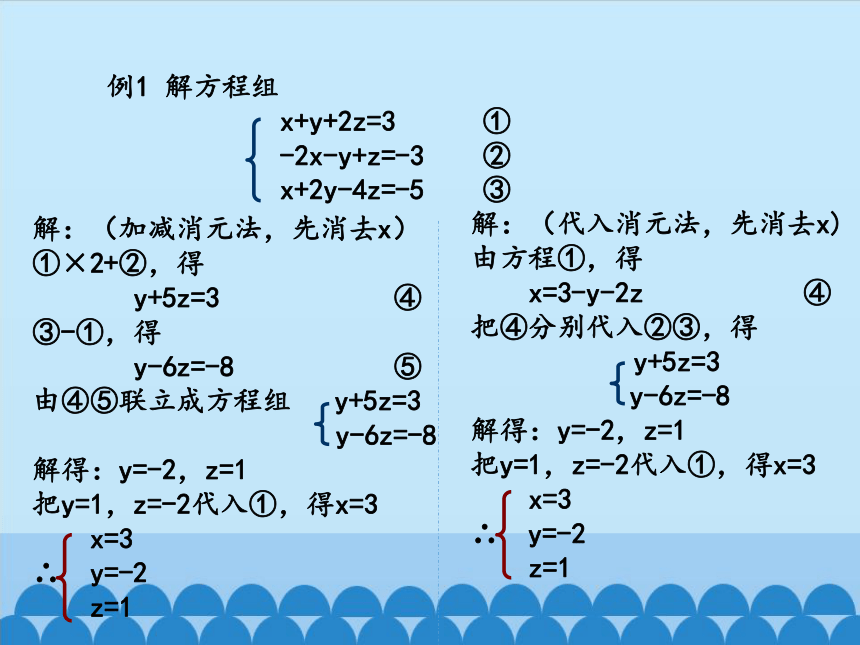
例1 解方程组
x+y+2z=3 ①
-2x-y+z=-3 ②
x+2y-4z=-5 ③
解:(加减消元法,先消去x)
①×2+②,得
y+5z=3 ④
③-①,得
y-6z=-8 ⑤
由④⑤联立成方程组 y+5z=3
y-6z=-8
解得:y=-2,z=1
把y=1,z=-2代入①,得x=3
x=3
∴ y=-2
z=1
解:(代入消元法,先消去x)
由方程①,得
x=3-y-2z ④
把④分别代入②③,得
y+5z=3
y-6z=-8
解得:y=-2,z=1
把y=1,z=-2代入①,得x=3
x=3
∴ y=-2
z=1
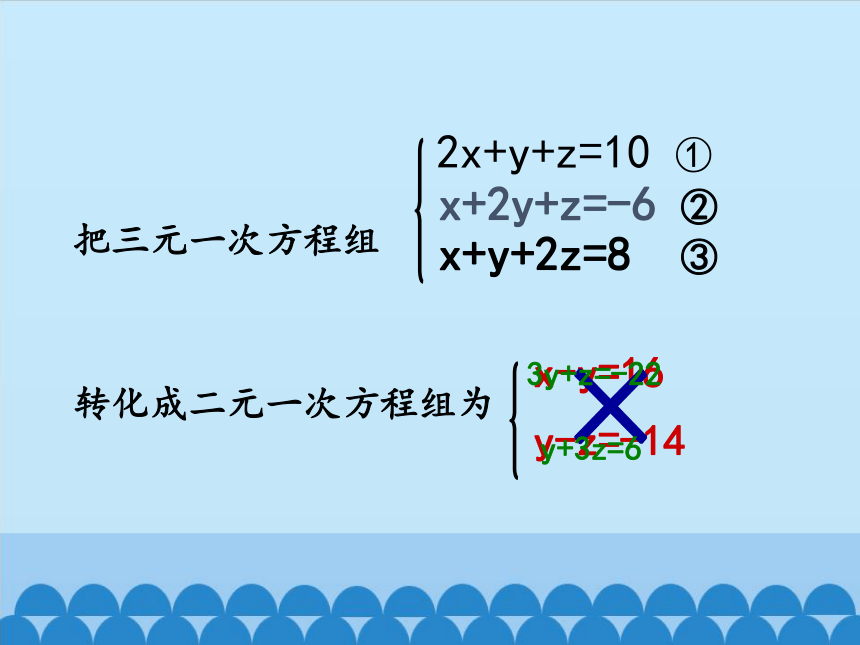
2x+y+z=10 ①
把三元一次方程组
x+2y+z=-6 ②
x+y+2z=8 ③
转化成二元一次方程组为
x-y=16
y-z=-14
×
3y+z=-22
y+3z=6
例2 解这个方程组
解:将方程③前移为第1个方程,将方程①和②分别后移为第2个和第3个方程,得
④ ⑤ ⑥
⑤-④×3,⑥-④×2,得:
⑧+⑦×(- ):得
所以原方程组得解为
① ② ③
④ ⑦ ⑧
问题2:解三个方程都含有三个未知数的三元一次方程组时应该注意什么?
基本思路:通过“带入”或“加减”进行消元。
基本思想:消元(选择合适的未知数为消去的对象)。
例3 幼儿营养标准中要求一个幼儿每天所需的营养量中应包含35单位的铁、70单位的钙和35单位的维生素。 现有一营养师根据上面的标准给幼儿园小朋友们配餐,其中包含A,B,C三种食物,下表给出的是每份(50g)食物A,B,C分别所含的铁、钙和维生素的量(单位)
食物 铁 钙 维生素
A 5 20 5
B 5 10 15
C 10 10 5
(1)幼儿园设食谱中三种食物各为x,y,z三份,请列出方程
组,使得A,B,C三种食物中所含的营养量刚好满足幼儿营养
标准的要求。
(2)解该三元一次方程组,求满足要求的A,B,C的份数。
5x
5y
10z
20x
10y
10z
5z
15y
5x
z
y
x
1.解方程组
?
巩固新知
2.某商场计划60000元从某厂家购进若干部手机,以满足市场需求。已知该厂家生产的甲,乙,丙三种型号手机,出厂价分别为每部1800元,600元和1200元。该商场用60000元恰好购买上述三种型号手机共40部,因市场需求甲型号手机比丙型号手机多购买了24部,求该商场购买了上述三种型号手机各多少部?
3.甲地到乙地全程是3.3km,一段上坡,一段平路,一段下坡。如果保持上坡每小时行3km,平路每小时行4km,下坡每小时行5km,那么从甲地到乙地需行51分,从乙地到甲地需行53.4分。求从甲地到乙地时上坡、平路、下坡的路程各是多少?
如何解三元一次方程组
解三元一次方程组的基本思路与解二元一次方程组的基本思路一样,即
三元一次方程组
消元
二元一次方程组
消元
一元一次方程
x+y+z=26
(1)
2x+2z=6
4x+2y+5z=4
(2)
2x+3y-z=4
3x-y+z=8
2x-y+3z=1
解下列方程组:
谢 谢
三元一次方程组及其解法
《九章算术 》方程中第一题:
今有上禾三秉,中禾二秉,下禾一秉,实三十九斗;上禾二秉,中禾三秉,下禾一秉,实三十四斗;上禾一秉,中禾二秉,下禾三秉,实二十六斗。问上、中、下禾实一秉各几何?
解:设上、中、下等稻子(禾)每捆(秉)可出谷子(实)分别x、y、z(斗),可得
3x+2y+z=39
2x+3y+z=34
x+2y+3z=26
定义:由三个一次方程组成的含三个未知数的方程组,
叫三元一次方程组。
(1)回顾解二元一次方程组的思路。
想一想
二元一次方程组
一元一次方程
消元
(2)消元方法:
① 代入法(代入消元法)
② 加减法(加减消元法)
设1元、2元、5元的纸币分别为x张、y张、z张
根据题意,可以得到下面三个方程:
x+y+z=12
x+4y-z=15
x+2y+5z=22
①
②
③
观察方程你能得出什么?
都含有三个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做三元一次方程。
这个问题的解必须同时满足上面三个条件,因此,我们把这三个方程合在一起,写成
x+y+z=12
x+4y-z=15
x+2y+5z=22
{
这个方程组含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组。
例1 解方程组
x+y+2z=3 ①
-2x-y+z=-3 ②
x+2y-4z=-5 ③
解:(加减消元法,先消去x)
①×2+②,得
y+5z=3 ④
③-①,得
y-6z=-8 ⑤
由④⑤联立成方程组 y+5z=3
y-6z=-8
解得:y=-2,z=1
把y=1,z=-2代入①,得x=3
x=3
∴ y=-2
z=1
解:(代入消元法,先消去x)
由方程①,得
x=3-y-2z ④
把④分别代入②③,得
y+5z=3
y-6z=-8
解得:y=-2,z=1
把y=1,z=-2代入①,得x=3
x=3
∴ y=-2
z=1
2x+y+z=10 ①
把三元一次方程组
x+2y+z=-6 ②
x+y+2z=8 ③
转化成二元一次方程组为
x-y=16
y-z=-14
×
3y+z=-22
y+3z=6
例2 解这个方程组
解:将方程③前移为第1个方程,将方程①和②分别后移为第2个和第3个方程,得
④ ⑤ ⑥
⑤-④×3,⑥-④×2,得:
⑧+⑦×(- ):得
所以原方程组得解为
① ② ③
④ ⑦ ⑧
问题2:解三个方程都含有三个未知数的三元一次方程组时应该注意什么?
基本思路:通过“带入”或“加减”进行消元。
基本思想:消元(选择合适的未知数为消去的对象)。
例3 幼儿营养标准中要求一个幼儿每天所需的营养量中应包含35单位的铁、70单位的钙和35单位的维生素。 现有一营养师根据上面的标准给幼儿园小朋友们配餐,其中包含A,B,C三种食物,下表给出的是每份(50g)食物A,B,C分别所含的铁、钙和维生素的量(单位)
食物 铁 钙 维生素
A 5 20 5
B 5 10 15
C 10 10 5
(1)幼儿园设食谱中三种食物各为x,y,z三份,请列出方程
组,使得A,B,C三种食物中所含的营养量刚好满足幼儿营养
标准的要求。
(2)解该三元一次方程组,求满足要求的A,B,C的份数。
5x
5y
10z
20x
10y
10z
5z
15y
5x
z
y
x
1.解方程组
?
巩固新知
2.某商场计划60000元从某厂家购进若干部手机,以满足市场需求。已知该厂家生产的甲,乙,丙三种型号手机,出厂价分别为每部1800元,600元和1200元。该商场用60000元恰好购买上述三种型号手机共40部,因市场需求甲型号手机比丙型号手机多购买了24部,求该商场购买了上述三种型号手机各多少部?
3.甲地到乙地全程是3.3km,一段上坡,一段平路,一段下坡。如果保持上坡每小时行3km,平路每小时行4km,下坡每小时行5km,那么从甲地到乙地需行51分,从乙地到甲地需行53.4分。求从甲地到乙地时上坡、平路、下坡的路程各是多少?
如何解三元一次方程组
解三元一次方程组的基本思路与解二元一次方程组的基本思路一样,即
三元一次方程组
消元
二元一次方程组
消元
一元一次方程
x+y+z=26
(1)
2x+2z=6
4x+2y+5z=4
(2)
2x+3y-z=4
3x-y+z=8
2x-y+3z=1
解下列方程组:
谢 谢
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
