沪科版数学七年级上册 4.5 角的比较与补(余)角课件(共14张PPT)
文档属性
| 名称 | 沪科版数学七年级上册 4.5 角的比较与补(余)角课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 151.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-18 11:03:10 | ||
图片预览



文档简介
(共14张PPT)
4.5 角的比较与补(余)角
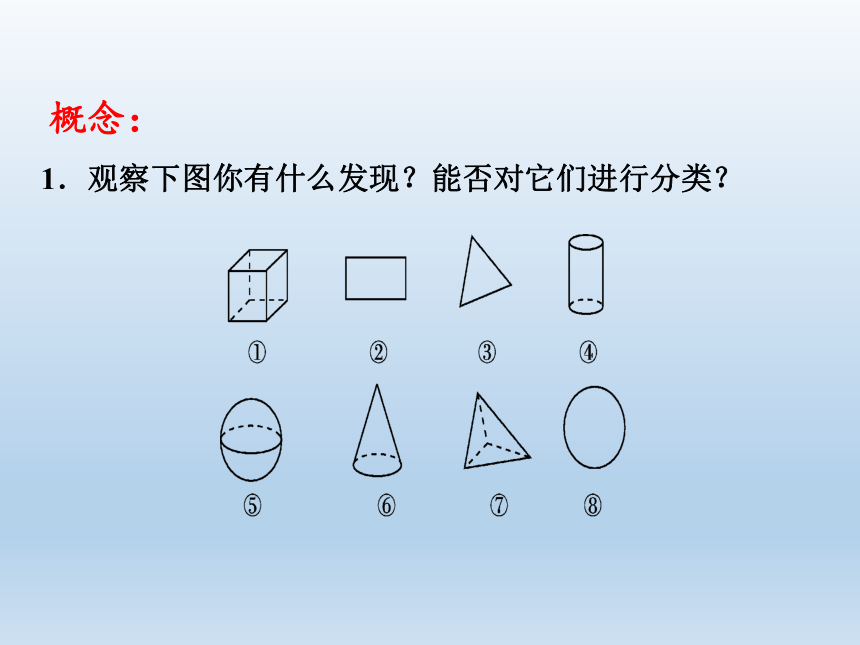
1.观察下图你有什么发现?能否对它们进行分类?
概念:
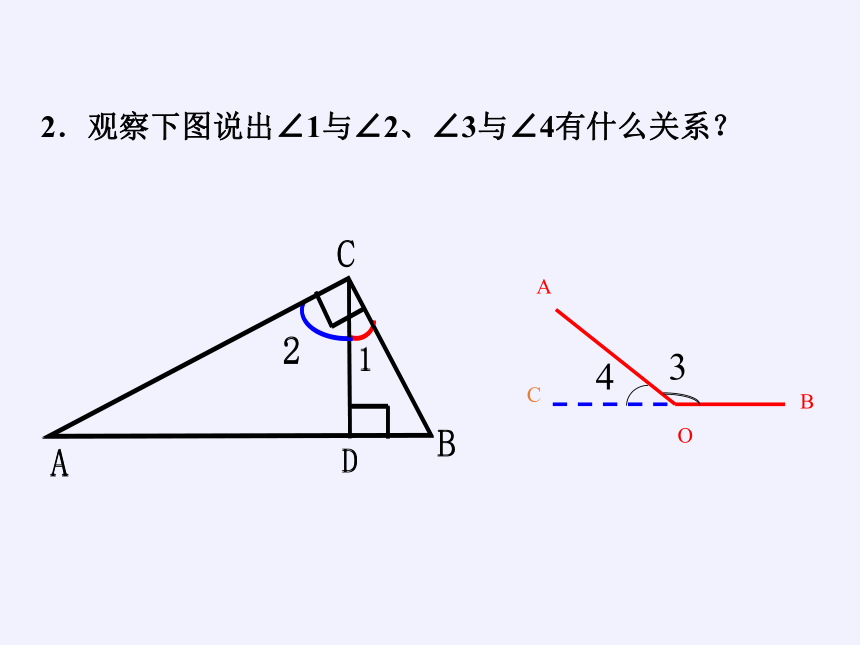
2.观察下图说出∠1与∠2、∠3与∠4有什么关系?
B
A
D
C
1
2
A
C
O
B
3
4
B
A
D
C
1
2
1.下列事实可以用同一个性质来解释的是( )
①墙上钉木条至少要两颗钉子才能牢固;
②农民拉绳插秧;
③解放军叔叔打靶瞄准;
④从A地到B地架设电线,为了节约材料,总是尽可能沿着线段AB架设.
A.①②④ B.① ② ③ C.② ③④ D.① ② ③④
性质:
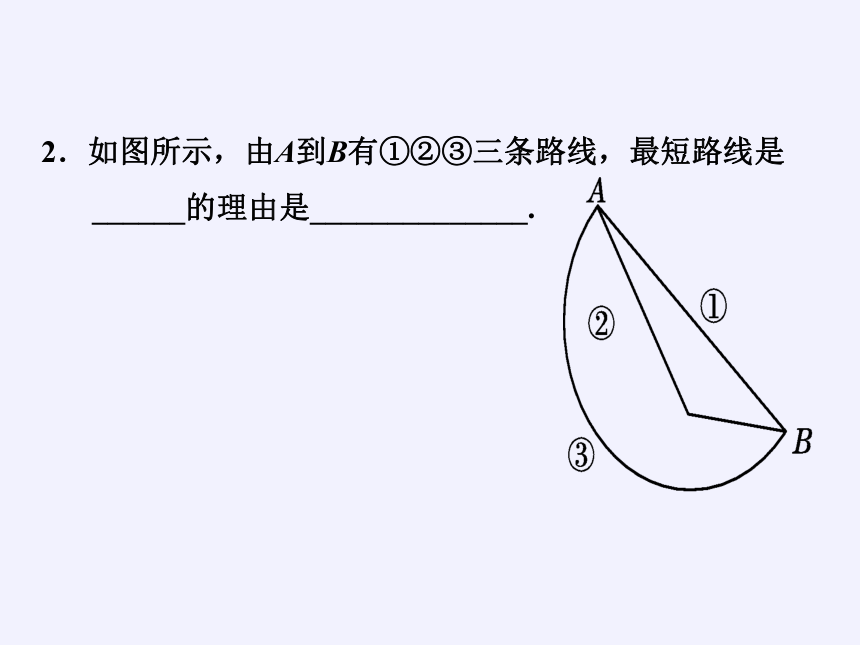
2.如图所示,由A到B有①②③三条路线,最短路线是______的理由是______________.
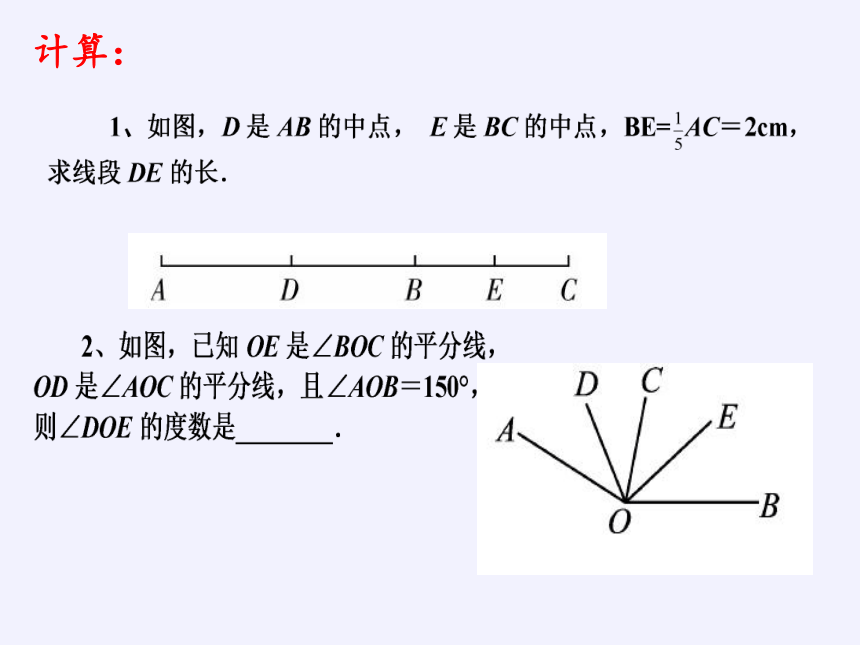
计算:
1、如图所示,OM,OB,ON是∠AOC内部的三条射线,OM,ON分别是∠AOB,∠BOC的平分线,∠NOC是∠AOM的3倍,∠BON比∠MOB大30°,求∠AOC的度数.
思想方法:
2、已知线段AB=12 cm,直线AB上有一点C,
且BC=6 cm,M是线段AC的中点,求线段AM的长.
2、已知∠AOB=60°,以OB为一边,作∠BOC=20°,求∠AOC的度数.
巩固练习:
1、如图,O是直线AB上一点,OC,OD
是从O点引出的两条射线,OE平分∠AOC,
∠BOC∶∠AOE∶∠AOD=2∶5∶8,
求∠BOD的度数.
今天我们学习了什么知识?你有哪些收获?还有什么问题吗?
小结:
概念:1、立体图形与平面图形
2、余角和补角
性质:1、两点确定一条直线
2、两点之间,线段最短。
计算:1、线段的计算
2、角的计算 ················ 两种计算
思想方法:
1、方程思想
2、分类讨论思想 ·············· 两种思想
1、若一个角的补角等于它的余角的4 倍,
求这个角的度数。
2、如图,C,D,E将线段AB分成2∶3∶4∶5四部分,M,P,Q,N分别是AC,CD,DE,EB的中点,且MN=21,求线段PQ的长度.
作业:
必做题:
3、如图①点O是直线AB上一点,∠COD是直角,OE平分∠BOC.
(1)①若∠DOE=25°,求∠AOC的度数;
②若∠DOE=α,求∠AOC的度数(用含α的式子表示);
(2)将图①中的∠COD绕点O按顺时针方向旋转至图②所示位置.
探究∠DOE与∠AOC的度数之间的关系,写出你的结论,并说明
理由.
选做题:
谢 谢
4.5 角的比较与补(余)角
1.观察下图你有什么发现?能否对它们进行分类?
概念:
2.观察下图说出∠1与∠2、∠3与∠4有什么关系?
B
A
D
C
1
2
A
C
O
B
3
4
B
A
D
C
1
2
1.下列事实可以用同一个性质来解释的是( )
①墙上钉木条至少要两颗钉子才能牢固;
②农民拉绳插秧;
③解放军叔叔打靶瞄准;
④从A地到B地架设电线,为了节约材料,总是尽可能沿着线段AB架设.
A.①②④ B.① ② ③ C.② ③④ D.① ② ③④
性质:
2.如图所示,由A到B有①②③三条路线,最短路线是______的理由是______________.
计算:
1、如图所示,OM,OB,ON是∠AOC内部的三条射线,OM,ON分别是∠AOB,∠BOC的平分线,∠NOC是∠AOM的3倍,∠BON比∠MOB大30°,求∠AOC的度数.
思想方法:
2、已知线段AB=12 cm,直线AB上有一点C,
且BC=6 cm,M是线段AC的中点,求线段AM的长.
2、已知∠AOB=60°,以OB为一边,作∠BOC=20°,求∠AOC的度数.
巩固练习:
1、如图,O是直线AB上一点,OC,OD
是从O点引出的两条射线,OE平分∠AOC,
∠BOC∶∠AOE∶∠AOD=2∶5∶8,
求∠BOD的度数.
今天我们学习了什么知识?你有哪些收获?还有什么问题吗?
小结:
概念:1、立体图形与平面图形
2、余角和补角
性质:1、两点确定一条直线
2、两点之间,线段最短。
计算:1、线段的计算
2、角的计算 ················ 两种计算
思想方法:
1、方程思想
2、分类讨论思想 ·············· 两种思想
1、若一个角的补角等于它的余角的4 倍,
求这个角的度数。
2、如图,C,D,E将线段AB分成2∶3∶4∶5四部分,M,P,Q,N分别是AC,CD,DE,EB的中点,且MN=21,求线段PQ的长度.
作业:
必做题:
3、如图①点O是直线AB上一点,∠COD是直角,OE平分∠BOC.
(1)①若∠DOE=25°,求∠AOC的度数;
②若∠DOE=α,求∠AOC的度数(用含α的式子表示);
(2)将图①中的∠COD绕点O按顺时针方向旋转至图②所示位置.
探究∠DOE与∠AOC的度数之间的关系,写出你的结论,并说明
理由.
选做题:
谢 谢
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
