28章 锐角三角函数(复习课)
文档属性
| 名称 | 28章 锐角三角函数(复习课) |

|
|
| 格式 | zip | ||
| 文件大小 | 341.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-24 00:00:00 | ||
图片预览





文档简介
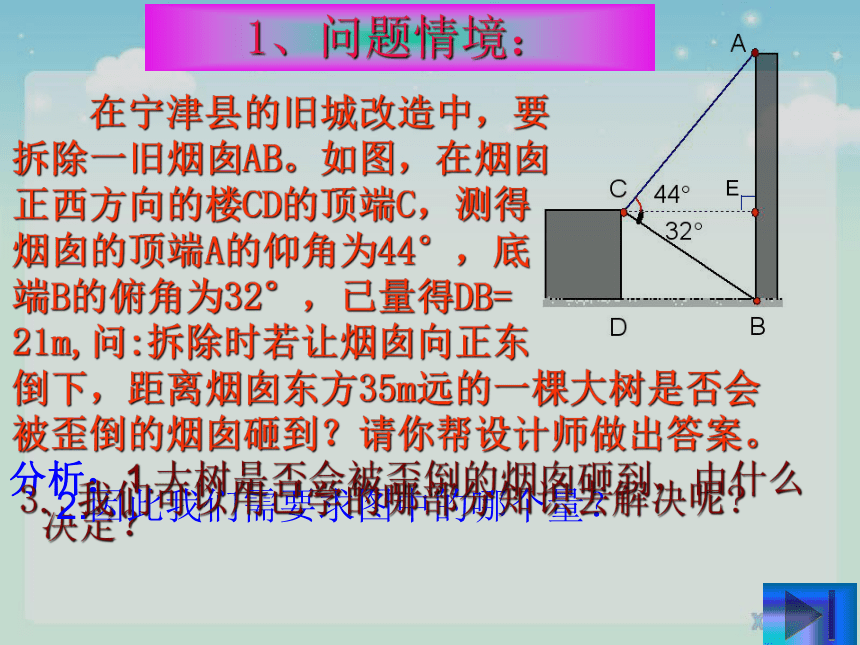
课件25张PPT。3.机遇能使人们成功,但成功者不都是机遇的恩赐!2.不求最好,但求更好!1.没有最好,只有更好!我努力,我进步!我耕耘,我收获…… 在宁津县的旧城改造中,要
拆除一旧烟囱AB。如图,在烟囱
正西方向的楼CD的顶端C,测得
烟囱的顶端A的仰角为44°,底
端B的俯角为32°,已量得DB=
21m,问:拆除时若让烟囱向正东
倒下,距离烟囱东方35m远的一棵大树是否会被歪倒的烟囱砸到?请你帮设计师做出答案。分析:1.大树是否会被歪倒的烟囱砸到,由什么决定?2.因此我们需要求图中的哪个量?3. 我们可以用已学的哪部分知识去解决呢?1、问题情境:28章 锐角三角函数
(复习课)2、复习目标 复习目标:1. 掌握锐角三角函数的基本知识,能利用解直角三角形的有关知识,解决生活中的实际问题;
2.进一步体会锐角三角函数的应用,提高数形结合、分析、解决问题的能力及应用数学的意识。
复习重点:锐角三角函数概念及性质的应用。
复习难点: 把实际问题转化为数学问题。1、锐角三角函数的定义 6⑴、正弦;
⑵、余弦;
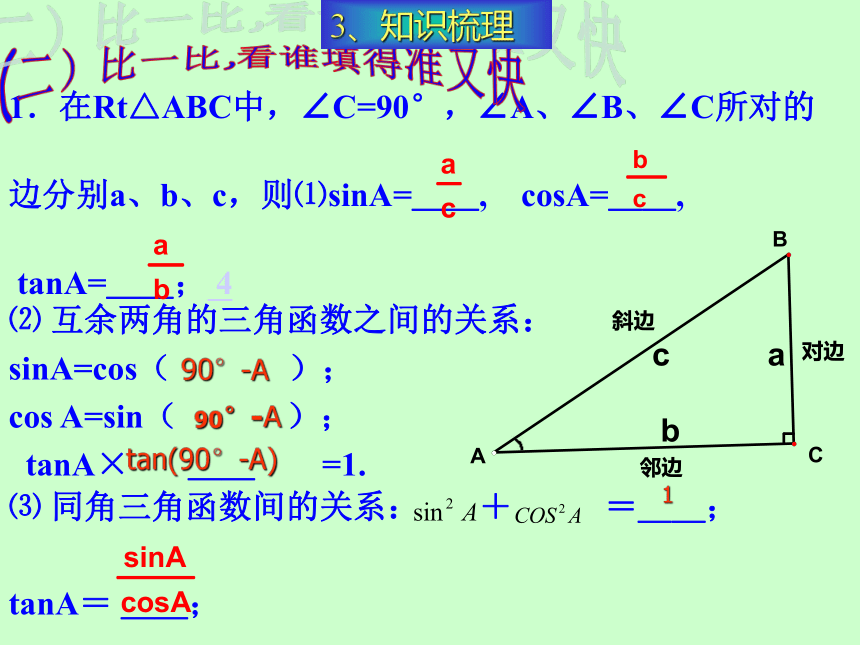
⑶、正切。3、30°、45°、60°特殊角的三角函数值。82、各锐角三角函数间的关系式 64.解直角三角形⑴、定义⑵解直角三角形用到的的关系式9⑶解直角三角形在实际问题中的应用 10。(一)本章知识结构图3、知识梳理1.在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的
边分别a、b、c,则⑴sinA=__, cosA=__,
tanA=__; 4⑵ 互余两角的三角函数之间的关系:
sinA=cos( );
cos A=sin( );
tanA× __ =1. ⑶ 同角三角函数间的关系: + =__;
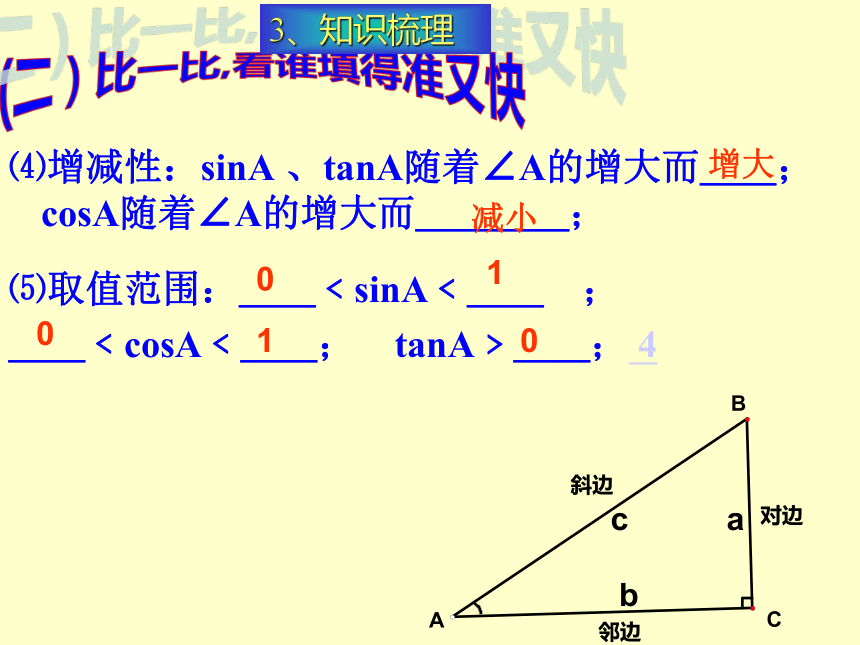
tanA= __;(二)比一比,看谁填得准又快190°-A90°-Atan(90°-A)3、知识梳理⑸取值范围:__﹤sinA﹤__ ;
__﹤cosA﹤__; tanA﹥__; 4⑷增减性:sinA 、tanA随着∠A的增大而__;cosA随着∠A的增大而____;(二)比一比,看谁填得准又快增大减小010103、知识梳理
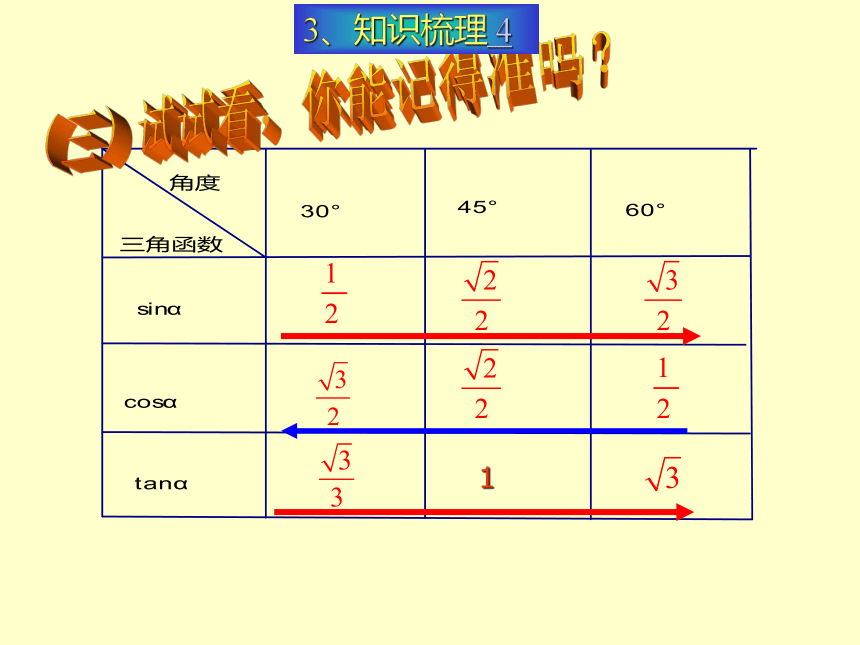
(三)试试看,你能记得准吗?
13、知识梳理 4(四)解直角三角形常用关系式,
你能说出全部吗?(1)三边关系:(2)两锐角关系:(3)边角关系:3、知识梳理4实际问题画出平面图形数学问题(解直角三角形的问题)选用恰当关系式解直角三角形,得到数学问题的答案检验实际问题的解答3、知识梳理(五)用解直角三角形的知识解决实际问题的一般步骤是什么,你记得吗?
1.锐角三角函数概念的考查
例1.(2008年甘南州)在正方形
网格中,∠α的位置如图所示,
则sinα的值为( ) 。 22
A B C D
思路点拨:本题通过网格的特征给出解题信息,是近几年中考题的常见题型。解决这类问题的思路是依据图形确定三角形的三边的长,然后根据定义进行计算。 αB 4、考点热点透析2.特殊角的三角函数值例2.(2 008年自贡市)已知α为锐角,且
tan(90°-α)= ,则α等于( )。
A 30° B 60 ° C 45° D 75°
例3. (2010·绵阳)
思路点拨:此类题通常根据已知条件和特殊角的三角函数值列方程求解,注意将特殊角的三角函数值记熟、记准。思路点拨:此类题是特殊角三角函数值的一种典型应用,求解时需熟悉特殊角三角函数值及有关运算法则。4、考点热点透析B原式=3.
3.解直角三角形
例4.(2010三明)如图,在梯形ABCD中,
AD∥BC,AC⊥AB,AD=CD,cos∠DCA
= ,BC=10,则AB的值是( )。
A 9 B 8 C 6 D 34、考点热点透析思路点拨: 此类题一般先由三角函数定义求出三角形一边的长,再由勾股定理求出
另一边的长。C4、考点热点透析例5. 海中有一个小岛P,它的
周围18海里内有暗礁,渔船跟
踪鱼群由西向东航行,在点A
测得小岛P在北偏东60 °方向
上,航行12海里到达B点,这
时测得小岛P在北偏东45°方
向上。如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由。分析:渔船是否有触礁危险,关键是看渔船在其航线上离小岛最近处是否超过18海里:若超过,则无危险;若不超过,则有危险。4.解直角三角形的应用解:过点P作PD⊥AC于点D,设
PD=x海里,由题意 得,∠PAC
=30°, ∠PBC=45°。在
Rt△PAD中,tan ∠PAC= = ,
∴AD= =
同理:在Rt△PBD中,BD= = =x
又∵AD-BD=12, ∴ -x=12,
解得,x=6+ =16.3海里﹤18海里
∴如果渔船不改变航线继续向东航行,有触礁危险.4、考点热点透析思路方法点拨 此类解直角三角形的应用问题在近几年越来越成为考试的热点问题。解题关键是从实际问题中抽象出数学问题,并找出所要求解的直角三角形,从而利用解直角三角形的有关知识求出实际问题的答案。5、 归纳小结你会了吗?这节课你学到了什么?你有什么收获?你还想知道什么?1.锐角三角函数概念;
2.特殊角的三角函数值;
3.解直角三角形1.如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正切值等于﹍﹍﹍。6.达标检测
2.A 关于原点对称的点B 的坐标
是( ).AACDB6.达标检测6.达标检测3.(2010广东中山)如图,已知Rt△ABC中,斜边BC上的高AD =
4,cosB= ,则
AC=____________。
5解:由图可知,∠ACE=44。,
∠BCE=32。,,四边形CDBE是矩形,
△ACE是直角三角形,∴CE=BD=21m.
在Rt△ACE中,tan ∠ ACE=
∴AE=CE×tan∠ACE=21×tan44°≈20.28
在Rt△ACE中,tan ∠ ACE=
∴AE=CE×tan∠BCE=21×tan32°≈13.12
∴AB=AE+BE ≈ 20.28 +13.12=33.4(m)
∵33.4m<35m ∴大树不会被歪倒的烟囱砸到。6.达标检测祝你成功不求能够超越别人,但求能够超越自己!1.如图所示,在正方形
网格中,∠α的位置如图所示,则sinα的值为( ) 。104、考点热点透析典例讲解:1.如图所示,边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)用铅笔画AD∥BC(D为格点);
(2)线段CD的长为------------;
(3)请在△ACD的三个内角中任
选一个锐角,若你所选的锐角是
--------,则它所对应的正弦函数值
是----------;
(4)若E为BC的中点,则tan ∠CAE的值是 4、考点热点透析16例5(2010年无锡)在东西方向的
海岸线上有一长为1km的码头MN
(如图),在码头西端M 的正西
19.5 km 处有一观察站A.某时
刻测得一艘匀速直线航行的
轮船位于 A 的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距 km的C处.(1)求该轮船航行的速度(保留精确结果);
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.
拆除一旧烟囱AB。如图,在烟囱
正西方向的楼CD的顶端C,测得
烟囱的顶端A的仰角为44°,底
端B的俯角为32°,已量得DB=
21m,问:拆除时若让烟囱向正东
倒下,距离烟囱东方35m远的一棵大树是否会被歪倒的烟囱砸到?请你帮设计师做出答案。分析:1.大树是否会被歪倒的烟囱砸到,由什么决定?2.因此我们需要求图中的哪个量?3. 我们可以用已学的哪部分知识去解决呢?1、问题情境:28章 锐角三角函数
(复习课)2、复习目标 复习目标:1. 掌握锐角三角函数的基本知识,能利用解直角三角形的有关知识,解决生活中的实际问题;
2.进一步体会锐角三角函数的应用,提高数形结合、分析、解决问题的能力及应用数学的意识。
复习重点:锐角三角函数概念及性质的应用。
复习难点: 把实际问题转化为数学问题。1、锐角三角函数的定义 6⑴、正弦;
⑵、余弦;
⑶、正切。3、30°、45°、60°特殊角的三角函数值。82、各锐角三角函数间的关系式 64.解直角三角形⑴、定义⑵解直角三角形用到的的关系式9⑶解直角三角形在实际问题中的应用 10。(一)本章知识结构图3、知识梳理1.在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的
边分别a、b、c,则⑴sinA=__, cosA=__,
tanA=__; 4⑵ 互余两角的三角函数之间的关系:
sinA=cos( );
cos A=sin( );
tanA× __ =1. ⑶ 同角三角函数间的关系: + =__;
tanA= __;(二)比一比,看谁填得准又快190°-A90°-Atan(90°-A)3、知识梳理⑸取值范围:__﹤sinA﹤__ ;
__﹤cosA﹤__; tanA﹥__; 4⑷增减性:sinA 、tanA随着∠A的增大而__;cosA随着∠A的增大而____;(二)比一比,看谁填得准又快增大减小010103、知识梳理
(三)试试看,你能记得准吗?
13、知识梳理 4(四)解直角三角形常用关系式,
你能说出全部吗?(1)三边关系:(2)两锐角关系:(3)边角关系:3、知识梳理4实际问题画出平面图形数学问题(解直角三角形的问题)选用恰当关系式解直角三角形,得到数学问题的答案检验实际问题的解答3、知识梳理(五)用解直角三角形的知识解决实际问题的一般步骤是什么,你记得吗?
1.锐角三角函数概念的考查
例1.(2008年甘南州)在正方形
网格中,∠α的位置如图所示,
则sinα的值为( ) 。 22
A B C D
思路点拨:本题通过网格的特征给出解题信息,是近几年中考题的常见题型。解决这类问题的思路是依据图形确定三角形的三边的长,然后根据定义进行计算。 αB 4、考点热点透析2.特殊角的三角函数值例2.(2 008年自贡市)已知α为锐角,且
tan(90°-α)= ,则α等于( )。
A 30° B 60 ° C 45° D 75°
例3. (2010·绵阳)
思路点拨:此类题通常根据已知条件和特殊角的三角函数值列方程求解,注意将特殊角的三角函数值记熟、记准。思路点拨:此类题是特殊角三角函数值的一种典型应用,求解时需熟悉特殊角三角函数值及有关运算法则。4、考点热点透析B原式=3.
3.解直角三角形
例4.(2010三明)如图,在梯形ABCD中,
AD∥BC,AC⊥AB,AD=CD,cos∠DCA
= ,BC=10,则AB的值是( )。
A 9 B 8 C 6 D 34、考点热点透析思路点拨: 此类题一般先由三角函数定义求出三角形一边的长,再由勾股定理求出
另一边的长。C4、考点热点透析例5. 海中有一个小岛P,它的
周围18海里内有暗礁,渔船跟
踪鱼群由西向东航行,在点A
测得小岛P在北偏东60 °方向
上,航行12海里到达B点,这
时测得小岛P在北偏东45°方
向上。如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由。分析:渔船是否有触礁危险,关键是看渔船在其航线上离小岛最近处是否超过18海里:若超过,则无危险;若不超过,则有危险。4.解直角三角形的应用解:过点P作PD⊥AC于点D,设
PD=x海里,由题意 得,∠PAC
=30°, ∠PBC=45°。在
Rt△PAD中,tan ∠PAC= = ,
∴AD= =
同理:在Rt△PBD中,BD= = =x
又∵AD-BD=12, ∴ -x=12,
解得,x=6+ =16.3海里﹤18海里
∴如果渔船不改变航线继续向东航行,有触礁危险.4、考点热点透析思路方法点拨 此类解直角三角形的应用问题在近几年越来越成为考试的热点问题。解题关键是从实际问题中抽象出数学问题,并找出所要求解的直角三角形,从而利用解直角三角形的有关知识求出实际问题的答案。5、 归纳小结你会了吗?这节课你学到了什么?你有什么收获?你还想知道什么?1.锐角三角函数概念;
2.特殊角的三角函数值;
3.解直角三角形1.如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正切值等于﹍﹍﹍。6.达标检测
2.A 关于原点对称的点B 的坐标
是( ).AACDB6.达标检测6.达标检测3.(2010广东中山)如图,已知Rt△ABC中,斜边BC上的高AD =
4,cosB= ,则
AC=____________。
5解:由图可知,∠ACE=44。,
∠BCE=32。,,四边形CDBE是矩形,
△ACE是直角三角形,∴CE=BD=21m.
在Rt△ACE中,tan ∠ ACE=
∴AE=CE×tan∠ACE=21×tan44°≈20.28
在Rt△ACE中,tan ∠ ACE=
∴AE=CE×tan∠BCE=21×tan32°≈13.12
∴AB=AE+BE ≈ 20.28 +13.12=33.4(m)
∵33.4m<35m ∴大树不会被歪倒的烟囱砸到。6.达标检测祝你成功不求能够超越别人,但求能够超越自己!1.如图所示,在正方形
网格中,∠α的位置如图所示,则sinα的值为( ) 。104、考点热点透析典例讲解:1.如图所示,边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)用铅笔画AD∥BC(D为格点);
(2)线段CD的长为------------;
(3)请在△ACD的三个内角中任
选一个锐角,若你所选的锐角是
--------,则它所对应的正弦函数值
是----------;
(4)若E为BC的中点,则tan ∠CAE的值是 4、考点热点透析16例5(2010年无锡)在东西方向的
海岸线上有一长为1km的码头MN
(如图),在码头西端M 的正西
19.5 km 处有一观察站A.某时
刻测得一艘匀速直线航行的
轮船位于 A 的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距 km的C处.(1)求该轮船航行的速度(保留精确结果);
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.
