2021-2022学年湖南省常德市澧县八年级(上)期中数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年湖南省常德市澧县八年级(上)期中数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 665.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-18 09:25:32 | ||
图片预览




文档简介
2021-2022学年湖南省常德市澧县八年级第一学期期中数学试卷
一、选择题(本大题共8个小题,每小题只有一个选项符合题意,每小题3分,共24分)
1.如图,已知∠ABC=∠DCB,要使△ABC≌△DCB,只需添加一个条件,这个条件不能是( )
A.∠A=∠D B.∠ACB=∠DBC C.AC=BD D.AB=DC
2.如图,为了让电线杆垂直于地面,工程人员的操作方法是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,E,C在同一直线上时,电线杆DE就垂直于BC,工程人员这种操作方法的依据是( )
A.等边对等角 B.等角对等边
C.垂线段最短 D.等腰三角形“三线合一”
3.命题“如果a<0,b<0,那么ab>0”的逆命题是( )
A.如果a<0,b<o,那么ab<0 B.如果ab>0,那么a<0,b<0
C.如果a>0,b>0,那么a<0 D.如果ab<0,那么a>0,b>0
4.如图,在△ABC中,∠A=50°,∠C=60°,BD平分∠ABC,则∠BDC的度数是( )
A.85° B.80° C.75° D.70°
5.研究发现新冠肺炎病毒大小约为0.000000125米,数0.000000125用科学记数法表示为( )
A.125×10﹣9 B.12.5×10﹣8 C.1.25×10﹣7 D.1.25×10﹣6
6.÷计算结果为( )
A. B. C. D.
7.已知x≠0,y≠0,对下列各个分式的约分,正确的是( )
A.= B.=
C.= D.
8.当x分别取2020、2018、2016、…、2、0、、、…、、、时,计算分式的值,再将所得结果相加,其和等于( )
A.﹣1 B.1 C.0 D.2020
二、填空题(每小题3分,共24分)
9.要使分式有意义,则x的取值范围为 .
10.如图,在△ABC中,AB=10,AD垂直平分线段BC,垂足为点D,点E是AC的中点,则EC的长为 .
11.计算:(﹣5)0+(﹣)2= .
12.下列句子:①爸爸你去哪儿呢?②舌尖上的中国;③中国好声音是选秀节目;④邱波是喀山世锦赛十米跳台的冠军;⑤你不是调皮捣蛋的坏孩子;⑥奔跑吧兄弟!是命题的有 (只填序号).
13.分式方程+1=的解是 .
14.计算:2= .
15.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,且a=3,b=4,若三边长为连续整数,则c= .
16.如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,EF=BF,则∠EFC= °.
三、解答题(共52分)
17.(1)计算:;
(2)解方程:.
18.先化简,再求值:÷(﹣),其中x=,y=﹣.
19.请按以下要求作图(不写作法,保留作图痕迹).
用直尺和圆规作△DEF,使得△DEF≌△ABC,并指出判定△DEF≌△ABC的依据(请在作图区内画图).
20.如图,D是BC上一点,AB=AD,BC=DE,AC=AE,求证:∠CDE=∠BAD.
21.某超市在中秋节前准备购进A、B两种品牌的月饼进行销售,据了解,用6000元购买A品牌月饼的数量比用4800元购买B品牌月饼的数量多80袋,且每袋B品牌月饼是每袋A品牌月饼价格的1.2倍.求每袋A品牌月饼的价格.
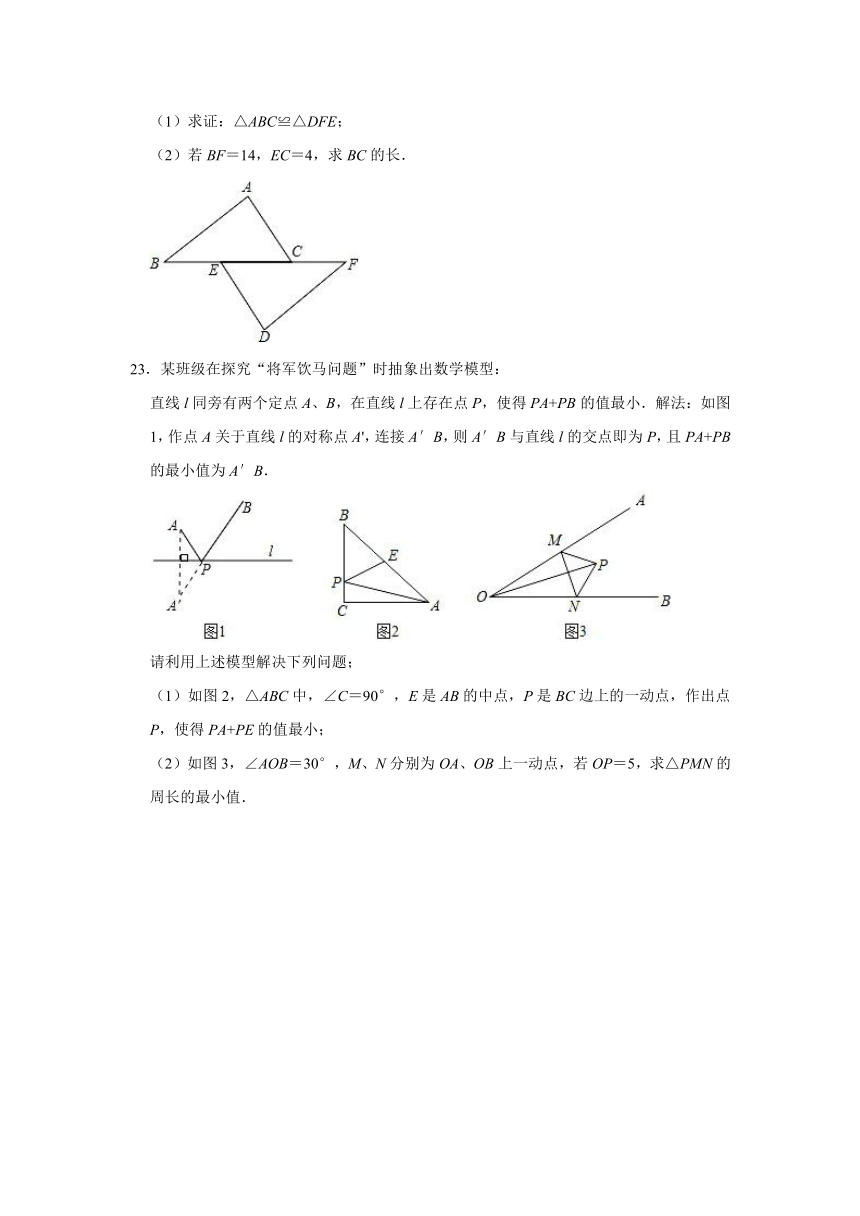
22.如图,已知点B,E,C,F在一条直线上,BE=CF,AC∥DE,∠A=∠D.
(1)求证:△ABC≌△DFE;
(2)若BF=14,EC=4,求BC的长.
23.某班级在探究“将军饮马问题”时抽象出数学模型:
直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.解法:如图1,作点A关于直线l的对称点A',连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.
请利用上述模型解决下列问题;
(1)如图2,△ABC中,∠C=90°,E是AB的中点,P是BC边上的一动点,作出点P,使得PA+PE的值最小;
(2)如图3,∠AOB=30°,M、N分别为OA、OB上一动点,若OP=5,求△PMN的周长的最小值.
参考答案
一、选择题(本大题共8个小题,每小题只有一个选项符合题意,每小题3分,共24分)
1.如图,已知∠ABC=∠DCB,要使△ABC≌△DCB,只需添加一个条件,这个条件不能是( )
A.∠A=∠D B.∠ACB=∠DBC C.AC=BD D.AB=DC
【分析】根据全等三角形的判定方法分别对各个选项进行判断即可.
解:A、在△ABC和△DCB中,
,
∴△ABC≌△DCB(AAS),故本选项不符合题意;
B、在△ABC和△DCB中,
,
∴△ABC≌△DCB(ASA),故本选项不符合题意;
C、根据两边和其中一边的对角不能判断两三角形全等,故本选项符合题意;
D、在△ABC和△DCB中,
,
∴△ABC≌△DCB(SAS),故本选项不符合题意;
故选:C.
2.如图,为了让电线杆垂直于地面,工程人员的操作方法是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,E,C在同一直线上时,电线杆DE就垂直于BC,工程人员这种操作方法的依据是( )
A.等边对等角 B.等角对等边
C.垂线段最短 D.等腰三角形“三线合一”
【分析】根据等腰三角形的性质即可得到结论.
解:∵AB=AC,BE=CE,
∴AE⊥BC,
故工程人员这种操作方法的依据是等腰三角形“三线合一”,
故选:D.
3.命题“如果a<0,b<0,那么ab>0”的逆命题是( )
A.如果a<0,b<o,那么ab<0 B.如果ab>0,那么a<0,b<0
C.如果a>0,b>0,那么a<0 D.如果ab<0,那么a>0,b>0
【分析】根据互逆命题概念解答即可.
解:命题“如果a<0,b<0,那么ab>0”的逆命题是“如果ab>0,那么a<0,b<0”,
故选:B.
4.如图,在△ABC中,∠A=50°,∠C=60°,BD平分∠ABC,则∠BDC的度数是( )
A.85° B.80° C.75° D.70°
【分析】先根据∠A=50°,∠C=60°得出∠ABC的度数,再由BD平分∠ABC求出∠ABD的度数,再根据三角形的外角等于和它不相邻的内角的和解答.
解:∵∠A=50°,∠C=60°,
∴∠ABC=180°﹣∠A﹣∠C=180°﹣50°﹣60°=70°,
∵BD平分∠ABC,
∴∠ABD=∠ABC=×70°=35°,
∴∠BDC=∠A+∠ABD=50°+35°=85°,
故选:A.
5.研究发现新冠肺炎病毒大小约为0.000000125米,数0.000000125用科学记数法表示为( )
A.125×10﹣9 B.12.5×10﹣8 C.1.25×10﹣7 D.1.25×10﹣6
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数n由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.000000125=1.25×10﹣7,
故选:C.
6.÷计算结果为( )
A. B. C. D.
【分析】原式利用除法法则变形,约分即可得到结果.
解:原式= x(x﹣2)
=.
故选:B.
7.已知x≠0,y≠0,对下列各个分式的约分,正确的是( )
A.= B.=
C.= D.
【分析】根据各个选项中的式子可以计算出正确的结果,从而可以解答本题.
解:A、=,故不符合题意;
B、=,故不符合题意;
C、=,故符合题意;
D、分子x2与分母y2没有公因式,不能约分,故不符合题意.
故选:C.
8.当x分别取2020、2018、2016、…、2、0、、、…、、、时,计算分式的值,再将所得结果相加,其和等于( )
A.﹣1 B.1 C.0 D.2020
【分析】把互为倒数的两个数代入分式可得它们的和是0,把0代入分式得﹣1,故得出结果为﹣1.
解:当x=a(a≠0)时,=,
当x=时,==﹣,
即互为倒数的两个数代入分式的和为0,
当x=0时,=﹣1,
故选:A.
二、填空题(每小题3分,共24分)
9.要使分式有意义,则x的取值范围为 x≠﹣3 .
【分析】根据分式有意义,分母不等于0列不等式求解即可.
解:由题意得,x+3≠0,
解得x≠﹣3.
故答案为:x≠﹣3.
10.如图,在△ABC中,AB=10,AD垂直平分线段BC,垂足为点D,点E是AC的中点,则EC的长为 5 .
【分析】据AD垂直平分BC,可得出AB=AC,再由点E是AC的中点,即可得到答案.
解:∵AD垂直平分BC,
∴AB=AC,
∵AB=10,
∴AC=10,
∵点E是AC的中点,
∴EC=AC=5,
故答案为:5.
11.计算:(﹣5)0+(﹣)2= 1 .
【分析】直接利用零指数幂的性质以及有理数的乘方运算法则分别化简,再利用有理数的加法运算法则计算得出答案.
解:原式=1+
=1.
故答案为:1.
12.下列句子:①爸爸你去哪儿呢?②舌尖上的中国;③中国好声音是选秀节目;④邱波是喀山世锦赛十米跳台的冠军;⑤你不是调皮捣蛋的坏孩子;⑥奔跑吧兄弟!是命题的有 ③④⑤ (只填序号).
【分析】根据命题的概念判断即可.
解:①爸爸你去哪儿呢?②舌尖上的中国;⑥奔跑吧兄弟!,没有对一件事情作出判断,不是命题,
③中国好声音是选秀节目;④邱波是喀山世锦赛十米跳台的冠军;⑤你不是调皮捣蛋的坏孩子,是命题,
故答案为:③④⑤.
13.分式方程+1=的解是 x=﹣1 .
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解:两边都乘以x﹣1,得:x+x﹣1=﹣3,
解得:x=﹣1,
检验:当x=﹣1时,x﹣1=﹣2≠0,
所以原分式方程的解为x=﹣1,
故答案为:x=﹣1.
14.计算:2= .
【分析】首先计算乘方,把分子分母分别乘方,然后再计算乘法,分子分母同时除以2x2m2n,即可得答案.
解:原式= =.
故答案为:.
15.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,且a=3,b=4,若三边长为连续整数,则c= 2或5 .
【分析】根据三角形的三边关系求得第三边的取值范围,进一步确定第三边的长,由此得出答案即可.
解:∵a=3,b=4,
∴根据三角形的三边关系,得4﹣3<c<4+3.
即1<c<7,
∵若三边长为连续整数,
∴c=2或5
故答案为:2或5.
16.如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,EF=BF,则∠EFC= 45 °.
【分析】由DE垂直平分AB,根据线段垂直平分线的性质,可得AE=BE,又由BE⊥AC,可求得∠A=∠ABE=45°,然后由AB=AC,BF=EF,求得答案.
解:∵DE垂直平分AB,
∴AE=BE,
∴∠A=∠ABE,
∵BE⊥AC,
∴∠A=∠ABE=45°,
∵AB=AC
∴∠ABC=∠C=67.5°,
∴∠EBC=∠ABC﹣∠ABE=22.5°,
∵BF=EF,
∴∠BEF=∠EBC=22.5°,
∴∠EFC=∠EBC+∠BEF=45°.
故答案为:45.
三、解答题(共52分)
17.(1)计算:;
(2)解方程:.
【分析】(1)先因式分解,再通分,最后同分母相加,结果化为最简分式;
(2)先因式分解,再去分母、去括号、移项、合并同类项、把x系数化为一,最后一定检验.
解:(1)原式=+
=
=
=;
(2)x(x+2)﹣(x+2)(x﹣2)=8,
x2+2x﹣x2+4=8,
2x=8﹣4,
x=2,
经检验x=2为原方程的增根,
∴原方程无解.
18.先化简,再求值:÷(﹣),其中x=,y=﹣.
【分析】根据分式的加减运算以及乘除运算法则进行化简,然后将x与y的值代入原式即可求出答案.
解:原式=
=
=
=,
当x=,y=﹣时,
原式==6.
19.请按以下要求作图(不写作法,保留作图痕迹).
用直尺和圆规作△DEF,使得△DEF≌△ABC,并指出判定△DEF≌△ABC的依据(请在作图区内画图).
【分析】利用尺规作DE=BC,DF=BA,EF=CA,根据SSS即可判定△DEF≌△ABC.
解:作图如下:
△DEF就是所求,
判断依据是三边对应相等的两个三角形全等.
20.如图,D是BC上一点,AB=AD,BC=DE,AC=AE,求证:∠CDE=∠BAD.
【分析】根据SSS,即可证得△ABC≌△ADE,利用等式的性质证明即可.
【解答】证明:在△ABC与△ADE中,
,
∴△ABC≌△ADE(SSS),
∴∠ABC=∠ADE,
∴∠ADC=∠ADE+∠CDE=∠ABC+∠BAD
∴∠CDE=∠BAD
21.某超市在中秋节前准备购进A、B两种品牌的月饼进行销售,据了解,用6000元购买A品牌月饼的数量比用4800元购买B品牌月饼的数量多80袋,且每袋B品牌月饼是每袋A品牌月饼价格的1.2倍.求每袋A品牌月饼的价格.
【分析】设每袋A品牌月饼的价格为x元,则每袋B品牌月饼的价格为1.2x元,由题意:用6000元购买A品牌月饼的数量比用4800元购买B品牌月饼的数量多80袋,列出分式方程,解方程即可.
解:设每袋A品牌月饼的价格为x元,则每袋B品牌月饼的价格为1.2x元,
由题意得:﹣=80,
解得:x=25,
经检验,x=25是原方程的解,
答:每袋A品牌月饼的价格为25元.
22.如图,已知点B,E,C,F在一条直线上,BE=CF,AC∥DE,∠A=∠D.
(1)求证:△ABC≌△DFE;
(2)若BF=14,EC=4,求BC的长.
【分析】(1)根据AAS证明△ABC≌△DFE即可解决问题.
(2)求出BE的长即可解决问题.
【解答】(1)证明:∵AC∥DE,
∴∠ACB=∠DEF,
∵BE=CF,
∴BC=EF,
在△ABC和△DFE中,
,
∴△ABC≌△DFE(AAS).
(2)解:∵BF=14,EC=4,
∴BE+CF=14﹣4=10,
∵BE=CF,
∴BE=CF=5,
∴BC=BE+EC=5+4=9.
23.某班级在探究“将军饮马问题”时抽象出数学模型:
直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.解法:如图1,作点A关于直线l的对称点A',连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.
请利用上述模型解决下列问题;
(1)如图2,△ABC中,∠C=90°,E是AB的中点,P是BC边上的一动点,作出点P,使得PA+PE的值最小;
(2)如图3,∠AOB=30°,M、N分别为OA、OB上一动点,若OP=5,求△PMN的周长的最小值.
【分析】(1)作点A关于直线BC的对称点A1,连接A1E,交BC于P,点P即为所求;
(2)作点P关于直线OA的对称点F,作点P关于直线OB的对称点G,连接FG,分别交OA、OB于M、N,根据“将军饮马问题”得到△PMN的周长的最小值为FG,再证得△FOG为边长为5的等边三角形即可得出答案.
解:(1)作点A关于直线BC的对称点A1,连接A1E,交BC于P,
如图所示,点P即为所求;
(2)作点P关于直线OA的对称点F,作点P关于直线OB的对称点G,连接FG,
分别交OA、OB于M、N,如图:
根据“将军饮马问题”得到△PMN的周长的最小值为FG,
由轴对称的性质得:∠FOA=∠AOP,∠POB=∠GOB,
OP=OF,OP=OG,
∵∠AOP+∠POB=∠AOB=30°,OP=5,
∴∠FOG=∠FOA+∠AOP+∠POB+∠GOB=60°,OF=OG=5,
∴△FOG为边长为5的等边三角形,
∴FG=5,
∴△PMN的周长的最小值为5.
一、选择题(本大题共8个小题,每小题只有一个选项符合题意,每小题3分,共24分)
1.如图,已知∠ABC=∠DCB,要使△ABC≌△DCB,只需添加一个条件,这个条件不能是( )
A.∠A=∠D B.∠ACB=∠DBC C.AC=BD D.AB=DC
2.如图,为了让电线杆垂直于地面,工程人员的操作方法是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,E,C在同一直线上时,电线杆DE就垂直于BC,工程人员这种操作方法的依据是( )
A.等边对等角 B.等角对等边
C.垂线段最短 D.等腰三角形“三线合一”
3.命题“如果a<0,b<0,那么ab>0”的逆命题是( )
A.如果a<0,b<o,那么ab<0 B.如果ab>0,那么a<0,b<0
C.如果a>0,b>0,那么a<0 D.如果ab<0,那么a>0,b>0
4.如图,在△ABC中,∠A=50°,∠C=60°,BD平分∠ABC,则∠BDC的度数是( )
A.85° B.80° C.75° D.70°
5.研究发现新冠肺炎病毒大小约为0.000000125米,数0.000000125用科学记数法表示为( )
A.125×10﹣9 B.12.5×10﹣8 C.1.25×10﹣7 D.1.25×10﹣6
6.÷计算结果为( )
A. B. C. D.
7.已知x≠0,y≠0,对下列各个分式的约分,正确的是( )
A.= B.=
C.= D.
8.当x分别取2020、2018、2016、…、2、0、、、…、、、时,计算分式的值,再将所得结果相加,其和等于( )
A.﹣1 B.1 C.0 D.2020
二、填空题(每小题3分,共24分)
9.要使分式有意义,则x的取值范围为 .
10.如图,在△ABC中,AB=10,AD垂直平分线段BC,垂足为点D,点E是AC的中点,则EC的长为 .
11.计算:(﹣5)0+(﹣)2= .
12.下列句子:①爸爸你去哪儿呢?②舌尖上的中国;③中国好声音是选秀节目;④邱波是喀山世锦赛十米跳台的冠军;⑤你不是调皮捣蛋的坏孩子;⑥奔跑吧兄弟!是命题的有 (只填序号).
13.分式方程+1=的解是 .
14.计算:2= .
15.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,且a=3,b=4,若三边长为连续整数,则c= .
16.如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,EF=BF,则∠EFC= °.
三、解答题(共52分)
17.(1)计算:;
(2)解方程:.
18.先化简,再求值:÷(﹣),其中x=,y=﹣.
19.请按以下要求作图(不写作法,保留作图痕迹).
用直尺和圆规作△DEF,使得△DEF≌△ABC,并指出判定△DEF≌△ABC的依据(请在作图区内画图).
20.如图,D是BC上一点,AB=AD,BC=DE,AC=AE,求证:∠CDE=∠BAD.
21.某超市在中秋节前准备购进A、B两种品牌的月饼进行销售,据了解,用6000元购买A品牌月饼的数量比用4800元购买B品牌月饼的数量多80袋,且每袋B品牌月饼是每袋A品牌月饼价格的1.2倍.求每袋A品牌月饼的价格.
22.如图,已知点B,E,C,F在一条直线上,BE=CF,AC∥DE,∠A=∠D.
(1)求证:△ABC≌△DFE;
(2)若BF=14,EC=4,求BC的长.
23.某班级在探究“将军饮马问题”时抽象出数学模型:
直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.解法:如图1,作点A关于直线l的对称点A',连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.
请利用上述模型解决下列问题;
(1)如图2,△ABC中,∠C=90°,E是AB的中点,P是BC边上的一动点,作出点P,使得PA+PE的值最小;
(2)如图3,∠AOB=30°,M、N分别为OA、OB上一动点,若OP=5,求△PMN的周长的最小值.
参考答案
一、选择题(本大题共8个小题,每小题只有一个选项符合题意,每小题3分,共24分)
1.如图,已知∠ABC=∠DCB,要使△ABC≌△DCB,只需添加一个条件,这个条件不能是( )
A.∠A=∠D B.∠ACB=∠DBC C.AC=BD D.AB=DC
【分析】根据全等三角形的判定方法分别对各个选项进行判断即可.
解:A、在△ABC和△DCB中,
,
∴△ABC≌△DCB(AAS),故本选项不符合题意;
B、在△ABC和△DCB中,
,
∴△ABC≌△DCB(ASA),故本选项不符合题意;
C、根据两边和其中一边的对角不能判断两三角形全等,故本选项符合题意;
D、在△ABC和△DCB中,
,
∴△ABC≌△DCB(SAS),故本选项不符合题意;
故选:C.
2.如图,为了让电线杆垂直于地面,工程人员的操作方法是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,E,C在同一直线上时,电线杆DE就垂直于BC,工程人员这种操作方法的依据是( )
A.等边对等角 B.等角对等边
C.垂线段最短 D.等腰三角形“三线合一”
【分析】根据等腰三角形的性质即可得到结论.
解:∵AB=AC,BE=CE,
∴AE⊥BC,
故工程人员这种操作方法的依据是等腰三角形“三线合一”,
故选:D.
3.命题“如果a<0,b<0,那么ab>0”的逆命题是( )
A.如果a<0,b<o,那么ab<0 B.如果ab>0,那么a<0,b<0
C.如果a>0,b>0,那么a<0 D.如果ab<0,那么a>0,b>0
【分析】根据互逆命题概念解答即可.
解:命题“如果a<0,b<0,那么ab>0”的逆命题是“如果ab>0,那么a<0,b<0”,
故选:B.
4.如图,在△ABC中,∠A=50°,∠C=60°,BD平分∠ABC,则∠BDC的度数是( )
A.85° B.80° C.75° D.70°
【分析】先根据∠A=50°,∠C=60°得出∠ABC的度数,再由BD平分∠ABC求出∠ABD的度数,再根据三角形的外角等于和它不相邻的内角的和解答.
解:∵∠A=50°,∠C=60°,
∴∠ABC=180°﹣∠A﹣∠C=180°﹣50°﹣60°=70°,
∵BD平分∠ABC,
∴∠ABD=∠ABC=×70°=35°,
∴∠BDC=∠A+∠ABD=50°+35°=85°,
故选:A.
5.研究发现新冠肺炎病毒大小约为0.000000125米,数0.000000125用科学记数法表示为( )
A.125×10﹣9 B.12.5×10﹣8 C.1.25×10﹣7 D.1.25×10﹣6
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数n由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.000000125=1.25×10﹣7,
故选:C.
6.÷计算结果为( )
A. B. C. D.
【分析】原式利用除法法则变形,约分即可得到结果.
解:原式= x(x﹣2)
=.
故选:B.
7.已知x≠0,y≠0,对下列各个分式的约分,正确的是( )
A.= B.=
C.= D.
【分析】根据各个选项中的式子可以计算出正确的结果,从而可以解答本题.
解:A、=,故不符合题意;
B、=,故不符合题意;
C、=,故符合题意;
D、分子x2与分母y2没有公因式,不能约分,故不符合题意.
故选:C.
8.当x分别取2020、2018、2016、…、2、0、、、…、、、时,计算分式的值,再将所得结果相加,其和等于( )
A.﹣1 B.1 C.0 D.2020
【分析】把互为倒数的两个数代入分式可得它们的和是0,把0代入分式得﹣1,故得出结果为﹣1.
解:当x=a(a≠0)时,=,
当x=时,==﹣,
即互为倒数的两个数代入分式的和为0,
当x=0时,=﹣1,
故选:A.
二、填空题(每小题3分,共24分)
9.要使分式有意义,则x的取值范围为 x≠﹣3 .
【分析】根据分式有意义,分母不等于0列不等式求解即可.
解:由题意得,x+3≠0,
解得x≠﹣3.
故答案为:x≠﹣3.
10.如图,在△ABC中,AB=10,AD垂直平分线段BC,垂足为点D,点E是AC的中点,则EC的长为 5 .
【分析】据AD垂直平分BC,可得出AB=AC,再由点E是AC的中点,即可得到答案.
解:∵AD垂直平分BC,
∴AB=AC,
∵AB=10,
∴AC=10,
∵点E是AC的中点,
∴EC=AC=5,
故答案为:5.
11.计算:(﹣5)0+(﹣)2= 1 .
【分析】直接利用零指数幂的性质以及有理数的乘方运算法则分别化简,再利用有理数的加法运算法则计算得出答案.
解:原式=1+
=1.
故答案为:1.
12.下列句子:①爸爸你去哪儿呢?②舌尖上的中国;③中国好声音是选秀节目;④邱波是喀山世锦赛十米跳台的冠军;⑤你不是调皮捣蛋的坏孩子;⑥奔跑吧兄弟!是命题的有 ③④⑤ (只填序号).
【分析】根据命题的概念判断即可.
解:①爸爸你去哪儿呢?②舌尖上的中国;⑥奔跑吧兄弟!,没有对一件事情作出判断,不是命题,
③中国好声音是选秀节目;④邱波是喀山世锦赛十米跳台的冠军;⑤你不是调皮捣蛋的坏孩子,是命题,
故答案为:③④⑤.
13.分式方程+1=的解是 x=﹣1 .
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解:两边都乘以x﹣1,得:x+x﹣1=﹣3,
解得:x=﹣1,
检验:当x=﹣1时,x﹣1=﹣2≠0,
所以原分式方程的解为x=﹣1,
故答案为:x=﹣1.
14.计算:2= .
【分析】首先计算乘方,把分子分母分别乘方,然后再计算乘法,分子分母同时除以2x2m2n,即可得答案.
解:原式= =.
故答案为:.
15.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,且a=3,b=4,若三边长为连续整数,则c= 2或5 .
【分析】根据三角形的三边关系求得第三边的取值范围,进一步确定第三边的长,由此得出答案即可.
解:∵a=3,b=4,
∴根据三角形的三边关系,得4﹣3<c<4+3.
即1<c<7,
∵若三边长为连续整数,
∴c=2或5
故答案为:2或5.
16.如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,EF=BF,则∠EFC= 45 °.
【分析】由DE垂直平分AB,根据线段垂直平分线的性质,可得AE=BE,又由BE⊥AC,可求得∠A=∠ABE=45°,然后由AB=AC,BF=EF,求得答案.
解:∵DE垂直平分AB,
∴AE=BE,
∴∠A=∠ABE,
∵BE⊥AC,
∴∠A=∠ABE=45°,
∵AB=AC
∴∠ABC=∠C=67.5°,
∴∠EBC=∠ABC﹣∠ABE=22.5°,
∵BF=EF,
∴∠BEF=∠EBC=22.5°,
∴∠EFC=∠EBC+∠BEF=45°.
故答案为:45.
三、解答题(共52分)
17.(1)计算:;
(2)解方程:.
【分析】(1)先因式分解,再通分,最后同分母相加,结果化为最简分式;
(2)先因式分解,再去分母、去括号、移项、合并同类项、把x系数化为一,最后一定检验.
解:(1)原式=+
=
=
=;
(2)x(x+2)﹣(x+2)(x﹣2)=8,
x2+2x﹣x2+4=8,
2x=8﹣4,
x=2,
经检验x=2为原方程的增根,
∴原方程无解.
18.先化简,再求值:÷(﹣),其中x=,y=﹣.
【分析】根据分式的加减运算以及乘除运算法则进行化简,然后将x与y的值代入原式即可求出答案.
解:原式=
=
=
=,
当x=,y=﹣时,
原式==6.
19.请按以下要求作图(不写作法,保留作图痕迹).
用直尺和圆规作△DEF,使得△DEF≌△ABC,并指出判定△DEF≌△ABC的依据(请在作图区内画图).
【分析】利用尺规作DE=BC,DF=BA,EF=CA,根据SSS即可判定△DEF≌△ABC.
解:作图如下:
△DEF就是所求,
判断依据是三边对应相等的两个三角形全等.
20.如图,D是BC上一点,AB=AD,BC=DE,AC=AE,求证:∠CDE=∠BAD.
【分析】根据SSS,即可证得△ABC≌△ADE,利用等式的性质证明即可.
【解答】证明:在△ABC与△ADE中,
,
∴△ABC≌△ADE(SSS),
∴∠ABC=∠ADE,
∴∠ADC=∠ADE+∠CDE=∠ABC+∠BAD
∴∠CDE=∠BAD
21.某超市在中秋节前准备购进A、B两种品牌的月饼进行销售,据了解,用6000元购买A品牌月饼的数量比用4800元购买B品牌月饼的数量多80袋,且每袋B品牌月饼是每袋A品牌月饼价格的1.2倍.求每袋A品牌月饼的价格.
【分析】设每袋A品牌月饼的价格为x元,则每袋B品牌月饼的价格为1.2x元,由题意:用6000元购买A品牌月饼的数量比用4800元购买B品牌月饼的数量多80袋,列出分式方程,解方程即可.
解:设每袋A品牌月饼的价格为x元,则每袋B品牌月饼的价格为1.2x元,
由题意得:﹣=80,
解得:x=25,
经检验,x=25是原方程的解,
答:每袋A品牌月饼的价格为25元.
22.如图,已知点B,E,C,F在一条直线上,BE=CF,AC∥DE,∠A=∠D.
(1)求证:△ABC≌△DFE;
(2)若BF=14,EC=4,求BC的长.
【分析】(1)根据AAS证明△ABC≌△DFE即可解决问题.
(2)求出BE的长即可解决问题.
【解答】(1)证明:∵AC∥DE,
∴∠ACB=∠DEF,
∵BE=CF,
∴BC=EF,
在△ABC和△DFE中,
,
∴△ABC≌△DFE(AAS).
(2)解:∵BF=14,EC=4,
∴BE+CF=14﹣4=10,
∵BE=CF,
∴BE=CF=5,
∴BC=BE+EC=5+4=9.
23.某班级在探究“将军饮马问题”时抽象出数学模型:
直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.解法:如图1,作点A关于直线l的对称点A',连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.
请利用上述模型解决下列问题;
(1)如图2,△ABC中,∠C=90°,E是AB的中点,P是BC边上的一动点,作出点P,使得PA+PE的值最小;
(2)如图3,∠AOB=30°,M、N分别为OA、OB上一动点,若OP=5,求△PMN的周长的最小值.
【分析】(1)作点A关于直线BC的对称点A1,连接A1E,交BC于P,点P即为所求;
(2)作点P关于直线OA的对称点F,作点P关于直线OB的对称点G,连接FG,分别交OA、OB于M、N,根据“将军饮马问题”得到△PMN的周长的最小值为FG,再证得△FOG为边长为5的等边三角形即可得出答案.
解:(1)作点A关于直线BC的对称点A1,连接A1E,交BC于P,
如图所示,点P即为所求;
(2)作点P关于直线OA的对称点F,作点P关于直线OB的对称点G,连接FG,
分别交OA、OB于M、N,如图:
根据“将军饮马问题”得到△PMN的周长的最小值为FG,
由轴对称的性质得:∠FOA=∠AOP,∠POB=∠GOB,
OP=OF,OP=OG,
∵∠AOP+∠POB=∠AOB=30°,OP=5,
∴∠FOG=∠FOA+∠AOP+∠POB+∠GOB=60°,OF=OG=5,
∴△FOG为边长为5的等边三角形,
∴FG=5,
∴△PMN的周长的最小值为5.
同课章节目录
