24.1.2垂直于弦的直径
图片预览







文档简介
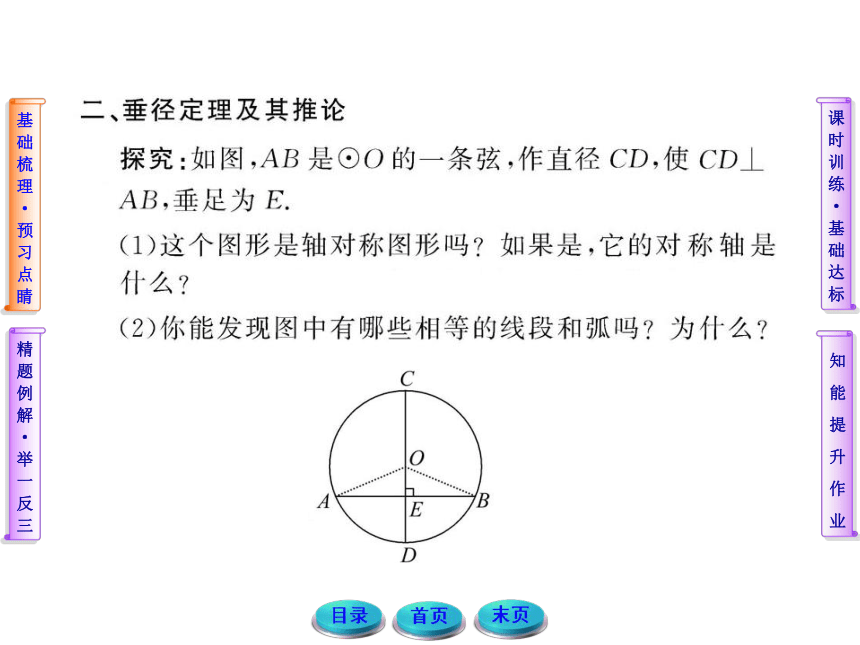
课件54张PPT。基础梳理 预习点睛 1.通过操作掌握圆的轴对称性.
2.掌握垂径定理及其推论的题设与结论. 1.通过折叠,应用轴对称图形的性质探究.
2.根据圆的轴对称性,应用轴对称图形的性质寻找相等的线段及弧,注意数学文字语言与符号语言之间的转换.精题例题 举一反三 应用垂径定理计算
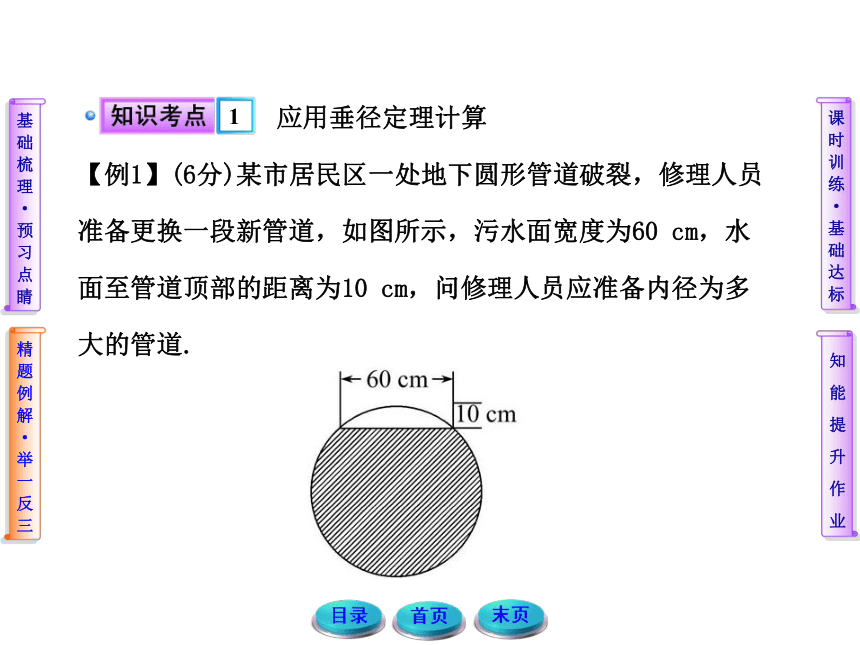
【例1】(6分)某市居民区一处地下圆形管道破裂,修理人员准备更换一段新管道,如图所示,污水面宽度为60 cm,水面至管道顶部的距离为10 cm,问修理人员应准备内径为多大的管道.【解题导引】根据实际问题抽象出数学模型,结合垂径定理,构造直角三角形,在直角三角形中运用勾股定理构建关于半径的方程.【规范解答】如图,弦AB表示污水水面,O为
圆心,过O作OD⊥AB于点D,与 交于点C,根
据垂径定理知,D是AB的中点,C是 的中点,
CD就是污水水面至管道顶部的距离,由题意可知:……2分
AB=60 cm,CD=10 cm,∴BD= AB=30 cm,OD=(r-10) cm.
………………………………………………………………3分
在Rt△DOB中,BD2+OD2=OB2,
即302+(r-10)2=r2 …………………………………………5分
解方程得r=50,
∴修理人员应准备内径为50 cm的管道.…………………6分 利用垂径定理进行计算,往往
与勾股定理结合使用,如图,弦长为a,圆心
到弦的距离为d,半径为r,弧的中点到弦的
距离(弓形的高)为h,在这四个量中,可以由
其中任意两个求其他两个,涉及到实际问题时,解题的关键是把实际问题抽象成数学问题,即画出符合题意的几何图形. 1.(2010·潍坊中考)如图,AB是⊙O的弦,半
径OC⊥AB于D点,且AB=6 cm,OD=4 cm,则
DC的长为( )
(A)5 cm (B)2.5 cm (C)2 cm (D)1 cm
【解析】选D.连接OA,由垂径定理得AD=3 cm,在Rt△AOD
中, 所以CD=OC-OD=1 cm.2.已知:如图,∠PAC=30°,在射
线AC上顺次截取AD=3 cm,DB=10 cm,
以DB为直径作⊙O交射线AP于E、F两
点,求圆心O到AP的距离及EF的长.【解析】过点O作OG⊥AP于点G,连接OF,
∵ DB=10,∴ OD=5,
∴ AO=AD+OD=3+5=8,
∵∠PAC=30°,
∴ OG= AO= ×8=4,
∵ OG⊥EF,∴ EG=GF,
∵ GF= =3,∴ EF=6 cm.
即圆心O到AP的距离为4 cm,EF的长为6 cm. 涉及到求圆的弦长时,一般过圆心作弦的垂线,构造直角三角形,应用垂径定理及勾股定理直接计算或构造方程求解. 与垂径定理有关的证明
【例2】如图,在⊙O中,AB、AC为互相垂
直且相等的两条弦,OD⊥AB于D,OE⊥AC于
E,求证:四边形ADOE是正方形.
【思路点拨】根据垂径定理及正方形的判
定进行证明.【自主解答】∵OE⊥AC,OD⊥AB,AB⊥AC,
∴∠OEA=90°,∠EAD=90°,∠ODA=90°.
∴四边形ADOE为矩形,AE= AC,AD= AB,
又∵AC=AB,∴AE=AD,∴四边形ADOE为正方形. 垂径定理及其推论反映了圆的轴对称性,是证明线段、角相等、两线垂直关系的重要依据,常作的辅助线有:一是作垂直于弦的直径,利用垂径定理解决问题;二是连接圆心与弦的中点,利用垂径定理的推论解决问题. 3.(2010·湖州中考)如图,已知⊙O的直径
AB⊥弦CD于点E.下列结论中一定正确的是
( )
(A)AE=OE (B)CE=DE
(C)OE= CE (D)∠AOC=60°
【解析】选B.根据垂径定理可得.4.(2010·佛山中考)如图,直线与两个同
心圆分别交于图示的各点,则下列结论中
正确的是( )
(A)MP与RN的大小关系不定 (B)MP=RN
(C)MP<RN (D)MP>RN
【解析】选B.过O点作OA⊥MN,垂足为A,由垂径定理得:AP=AR,AM=AN,所以AM-AP=AN-AR,即MP=RN. 在圆中,解有关弦的问题时,常常需要作“垂直于弦的直径”作为辅助线,实际上,往往只需从圆心作一条与弦垂直的线段即可. 课时训练 基础达标1.(2010·西宁中考)如图,在半径为5的⊙O
中,若弦AB=8,则△AOB的面积为( )
(A)24 (B)16
(C)12 (D)8
【解析】选C.过O点作OC⊥AB,垂足为C,则AC=BC=4,所以
所以△AOB的面积为
AB·OC=12.2.点P是半径为5的⊙O内一点,且OP=4,在过P点的所有⊙O的弦中,你认为弦长为整数的弦的条数为( )
(A)8条 (B)7条 (C)6条 (D)5条
【解析】选D.最短的弦长为2× =6,
最长的弦长为10,∴弦长为整数的弦有5条.3.(2010·毕节中考)如图,AB为⊙O的弦,
⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,
且CD=1,则弦AB的长是_____.
【解析】连接OA,在Rt△AOD中,OD=OC-CD=4,所以
所以AB=6.
答案:64.若圆的半径为R,则垂直平分半径的弦长等于_____.
【解析】如图,OC⊥AB于点D,则AD=BD.
又OA=OC=R,OD=CD,∴OD= R,
∴
答案:5.如图,AB是⊙O的直径,BC是弦,AC⊥BC, OD⊥BC于E,交
于D.
(1)请写出三个不同类型的正确结论;
(2)若BC=8,ED=2,求⊙O的半径. 【解析】(1)不同类型的正确结论有:
①BE=CE;② = ;③∠BED = 90°;④∠BOD=∠A;
⑤AC∥OD;⑥OE2+BE2=OB2;⑦S△ABC=BC·OE;
(答案不惟一)
(2)∵OD⊥BC,∴BE=CE= BC=4,
设⊙O的半径为R,则OE=OD-DE=R-2.
在Rt△OEB中,由勾股定理得:OE2+BE2=OB2,
即(R-2)2+42=R2,解得R=5,∴⊙O的半径为5.智能提升作业一、选择题(每小题4分,共12分)
1.(2010·梧州中考)如图,AB是⊙O的直径,
弦CD⊥AB于点E,则下列结论中一定正确的个
数有①CE=DE;②BE=OE;③ ;
④∠CAB=∠DAB; ⑤AC=AD.( )
(A)4个 (B)3个 (C)2个 (D)1个【解析】选A.根据垂径定理得,①、③、④正确,AB垂直平分CD,所以⑤也正确,故选A.2.(2010·乐山中考)如图,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为(-2,4),则该圆弧所在圆的圆心坐标是( )
(A)(-1,2) (B)(1,-1)
(C)(-1,1) (D)(2,1)【解析】选C.由题意根据A点的坐标建立如图所示的坐标系,由圆的对称性可知,圆心为弦AC、AB垂直平分线的交点,观察图象可知交点坐标为(-1,1).3.(2010·襄樊中考)已知⊙O的半径为13 cm,弦AB//CD,AB=24 cm,CD=10 cm,则AB、CD之间的距离为( )
(A)17 cm (B)7 cm
(C)12 cm (D)17 cm或7 cm【解析】选D.本题有两种情形:(1)当AB、CD在圆心O的异侧时,过O作OM⊥AB于M,延长MO交CD于N,连接OB、OD.如图1.
∵AB∥CD,MN⊥AB,∴MN⊥CD.
∵AB=24 cm,CD=10 cm,∴BM=12 cm,DN=5 cm,
在Rt△OMB与Rt△OND中,OB2=OM2+BM2,
OD2=DN2+ON2,∴OM=5 cm,ON=12 cm,
∴MN=OM+ON=5+12=17(cm);(2)当AB、CD在圆心O的同侧时,如图2.
同理可得OM=5 cm,ON=12 cm,
MN=ON-OM=12-5=7 (cm),
∴AB、CD之间的距离为17 cm或7 cm. 【归纳整合】(1)在半径为r的圆中,若弦AB=a,CD=b,且AB∥CD,AB、CD间的距离为h,在a、b、r、h这四个变量中已知三个量可以求出另外一个量.
(2)在解无图题时,要考虑不同的情形,分情况讨论问题,此种类型题常因考虑不周而漏解.二、填空题(每小题4分,共12分)
4.工程上常用钢珠来测量零件上小孔
的直径,假设钢珠的直径是10mm,测
得钢珠顶端离零件表面的距离为8mm,
如图所示,则这个小孔的直径AB是_____mm.【解析】过O作OC⊥AB,垂足为C,连接OA,
则△AOC为直角三角形.
又OC=3mm,OA=5mm,
在Rt△AOC中,
由勾股定理,得
AC= =4(mm).
由垂径定理,得AC=BC,∴AB=2AC=8mm.
答案:85.如图,点A、B是⊙O上的两点,AB=10,点P是⊙O上的动点(P与A、B不重合),连接AP、PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF=_____.
【解析】∵OE⊥AP,∴AE=PE,
同理:BF=PF,∴EF= AB=5.
答案:56.如图,⊙O的弦BA的延长线与半径OC
的延长线交于点P,且PA=AB=6 cm,
PO=12 cm,则⊙O的半径为_____.【解析】过O点作OD⊥AB于D,则BD=AD=3 cm,
∴PD=6+3=9 cm,
在Rt△PDO中
在Rt△ODB中,
答案: cm三、解答题(共26分)
7.(8分)(2010·长春中考)如图,
将一个两边都带有刻度的直尺放在半
圆形纸片上,使其一边经过圆心O,
另一边所在直线与半圆相交于点D、E,量出半径OC=5 cm,弦DE=8 cm.求直尺的宽.【解析】过点O作OM⊥DE于点M,连接OD.
∴DM= DE.
∵DE=8,∴DM=4.
在Rt△ODM中,∵OD=OC=5,
∴OM=
∴直尺的宽度为3 cm.8.(8分)已知正方形ABCD和矩形EFGH按如图位置摆放,且AD=EH=2,EF=4,一圆过A、B、F、E四点,求该圆半径的长. 【解析】记圆心为O点,并设⊙O的半径为r.对于AB、EF的中点M、N,连接MN、BO、FO,
由对称性可知:MN过圆心O点,且MN⊥AB,MN⊥EF,
∵AD=EH=2,EF=4,
∴BM=1,
NF=2,OF=OB=r,在Rt△OBM中,MB2+OM2=OB2=r2,即1+OM2=r2,
在Rt△OFN中,NF2+ON2=OF2=r2,即4+ON2=r2,
∴1+OM2=4+ON2,
又∵MN=4,∴1+(4-ON)2=4+ON2,
解得:ON= ,
把ON= 代入4+ON2=r2,得:
r2=4+( )2= ,∴r= ,
∴该圆的半径长为 .【拓展延伸】
9.(10分)有一座圆弧形的拱桥,桥下水平面宽7.2 m,拱顶高出水面2.4 m,现有一货船宽3 m,船舱顶部为长方体,高出水面2 m,问该货船能否顺利通过这座拱桥?【解析】如图所示, 表示桥拱,
AB=7.2 m,CD=2.4 m,EF=3 m,D为AB、
EF的中点,且CD、NF、ME均垂直于AB,
设 所在圆的圆心为O,连接OA及ON,连接OD,则C、D、O
共线.设OA=R m,
则OD=OC-DC=(R-2.4)m,
AD= AB=3.6 m,
由勾股定理有OA2=AD2+OD2,
即R2=3.62+(R-2.4)2,解得R=3.9(m).货船能否顺利通过该桥,关键是看货箱顶部两角(M、N)是
否被桥拱( )拦住,即当货船位于桥下正中位置时,货
箱顶部两角(M、N)到水平面(AB)的高度是否小于FN.
在Rt△ONG中,
所以FN=DG=OG-OD=OG-(OC-DC)
=3.6-(3.9-2.4)=2.1(m).
因为2<2.1,所以货船可以顺利通过该桥.
2.掌握垂径定理及其推论的题设与结论. 1.通过折叠,应用轴对称图形的性质探究.
2.根据圆的轴对称性,应用轴对称图形的性质寻找相等的线段及弧,注意数学文字语言与符号语言之间的转换.精题例题 举一反三 应用垂径定理计算
【例1】(6分)某市居民区一处地下圆形管道破裂,修理人员准备更换一段新管道,如图所示,污水面宽度为60 cm,水面至管道顶部的距离为10 cm,问修理人员应准备内径为多大的管道.【解题导引】根据实际问题抽象出数学模型,结合垂径定理,构造直角三角形,在直角三角形中运用勾股定理构建关于半径的方程.【规范解答】如图,弦AB表示污水水面,O为
圆心,过O作OD⊥AB于点D,与 交于点C,根
据垂径定理知,D是AB的中点,C是 的中点,
CD就是污水水面至管道顶部的距离,由题意可知:……2分
AB=60 cm,CD=10 cm,∴BD= AB=30 cm,OD=(r-10) cm.
………………………………………………………………3分
在Rt△DOB中,BD2+OD2=OB2,
即302+(r-10)2=r2 …………………………………………5分
解方程得r=50,
∴修理人员应准备内径为50 cm的管道.…………………6分 利用垂径定理进行计算,往往
与勾股定理结合使用,如图,弦长为a,圆心
到弦的距离为d,半径为r,弧的中点到弦的
距离(弓形的高)为h,在这四个量中,可以由
其中任意两个求其他两个,涉及到实际问题时,解题的关键是把实际问题抽象成数学问题,即画出符合题意的几何图形. 1.(2010·潍坊中考)如图,AB是⊙O的弦,半
径OC⊥AB于D点,且AB=6 cm,OD=4 cm,则
DC的长为( )
(A)5 cm (B)2.5 cm (C)2 cm (D)1 cm
【解析】选D.连接OA,由垂径定理得AD=3 cm,在Rt△AOD
中, 所以CD=OC-OD=1 cm.2.已知:如图,∠PAC=30°,在射
线AC上顺次截取AD=3 cm,DB=10 cm,
以DB为直径作⊙O交射线AP于E、F两
点,求圆心O到AP的距离及EF的长.【解析】过点O作OG⊥AP于点G,连接OF,
∵ DB=10,∴ OD=5,
∴ AO=AD+OD=3+5=8,
∵∠PAC=30°,
∴ OG= AO= ×8=4,
∵ OG⊥EF,∴ EG=GF,
∵ GF= =3,∴ EF=6 cm.
即圆心O到AP的距离为4 cm,EF的长为6 cm. 涉及到求圆的弦长时,一般过圆心作弦的垂线,构造直角三角形,应用垂径定理及勾股定理直接计算或构造方程求解. 与垂径定理有关的证明
【例2】如图,在⊙O中,AB、AC为互相垂
直且相等的两条弦,OD⊥AB于D,OE⊥AC于
E,求证:四边形ADOE是正方形.
【思路点拨】根据垂径定理及正方形的判
定进行证明.【自主解答】∵OE⊥AC,OD⊥AB,AB⊥AC,
∴∠OEA=90°,∠EAD=90°,∠ODA=90°.
∴四边形ADOE为矩形,AE= AC,AD= AB,
又∵AC=AB,∴AE=AD,∴四边形ADOE为正方形. 垂径定理及其推论反映了圆的轴对称性,是证明线段、角相等、两线垂直关系的重要依据,常作的辅助线有:一是作垂直于弦的直径,利用垂径定理解决问题;二是连接圆心与弦的中点,利用垂径定理的推论解决问题. 3.(2010·湖州中考)如图,已知⊙O的直径
AB⊥弦CD于点E.下列结论中一定正确的是
( )
(A)AE=OE (B)CE=DE
(C)OE= CE (D)∠AOC=60°
【解析】选B.根据垂径定理可得.4.(2010·佛山中考)如图,直线与两个同
心圆分别交于图示的各点,则下列结论中
正确的是( )
(A)MP与RN的大小关系不定 (B)MP=RN
(C)MP<RN (D)MP>RN
【解析】选B.过O点作OA⊥MN,垂足为A,由垂径定理得:AP=AR,AM=AN,所以AM-AP=AN-AR,即MP=RN. 在圆中,解有关弦的问题时,常常需要作“垂直于弦的直径”作为辅助线,实际上,往往只需从圆心作一条与弦垂直的线段即可. 课时训练 基础达标1.(2010·西宁中考)如图,在半径为5的⊙O
中,若弦AB=8,则△AOB的面积为( )
(A)24 (B)16
(C)12 (D)8
【解析】选C.过O点作OC⊥AB,垂足为C,则AC=BC=4,所以
所以△AOB的面积为
AB·OC=12.2.点P是半径为5的⊙O内一点,且OP=4,在过P点的所有⊙O的弦中,你认为弦长为整数的弦的条数为( )
(A)8条 (B)7条 (C)6条 (D)5条
【解析】选D.最短的弦长为2× =6,
最长的弦长为10,∴弦长为整数的弦有5条.3.(2010·毕节中考)如图,AB为⊙O的弦,
⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,
且CD=1,则弦AB的长是_____.
【解析】连接OA,在Rt△AOD中,OD=OC-CD=4,所以
所以AB=6.
答案:64.若圆的半径为R,则垂直平分半径的弦长等于_____.
【解析】如图,OC⊥AB于点D,则AD=BD.
又OA=OC=R,OD=CD,∴OD= R,
∴
答案:5.如图,AB是⊙O的直径,BC是弦,AC⊥BC, OD⊥BC于E,交
于D.
(1)请写出三个不同类型的正确结论;
(2)若BC=8,ED=2,求⊙O的半径. 【解析】(1)不同类型的正确结论有:
①BE=CE;② = ;③∠BED = 90°;④∠BOD=∠A;
⑤AC∥OD;⑥OE2+BE2=OB2;⑦S△ABC=BC·OE;
(答案不惟一)
(2)∵OD⊥BC,∴BE=CE= BC=4,
设⊙O的半径为R,则OE=OD-DE=R-2.
在Rt△OEB中,由勾股定理得:OE2+BE2=OB2,
即(R-2)2+42=R2,解得R=5,∴⊙O的半径为5.智能提升作业一、选择题(每小题4分,共12分)
1.(2010·梧州中考)如图,AB是⊙O的直径,
弦CD⊥AB于点E,则下列结论中一定正确的个
数有①CE=DE;②BE=OE;③ ;
④∠CAB=∠DAB; ⑤AC=AD.( )
(A)4个 (B)3个 (C)2个 (D)1个【解析】选A.根据垂径定理得,①、③、④正确,AB垂直平分CD,所以⑤也正确,故选A.2.(2010·乐山中考)如图,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为(-2,4),则该圆弧所在圆的圆心坐标是( )
(A)(-1,2) (B)(1,-1)
(C)(-1,1) (D)(2,1)【解析】选C.由题意根据A点的坐标建立如图所示的坐标系,由圆的对称性可知,圆心为弦AC、AB垂直平分线的交点,观察图象可知交点坐标为(-1,1).3.(2010·襄樊中考)已知⊙O的半径为13 cm,弦AB//CD,AB=24 cm,CD=10 cm,则AB、CD之间的距离为( )
(A)17 cm (B)7 cm
(C)12 cm (D)17 cm或7 cm【解析】选D.本题有两种情形:(1)当AB、CD在圆心O的异侧时,过O作OM⊥AB于M,延长MO交CD于N,连接OB、OD.如图1.
∵AB∥CD,MN⊥AB,∴MN⊥CD.
∵AB=24 cm,CD=10 cm,∴BM=12 cm,DN=5 cm,
在Rt△OMB与Rt△OND中,OB2=OM2+BM2,
OD2=DN2+ON2,∴OM=5 cm,ON=12 cm,
∴MN=OM+ON=5+12=17(cm);(2)当AB、CD在圆心O的同侧时,如图2.
同理可得OM=5 cm,ON=12 cm,
MN=ON-OM=12-5=7 (cm),
∴AB、CD之间的距离为17 cm或7 cm. 【归纳整合】(1)在半径为r的圆中,若弦AB=a,CD=b,且AB∥CD,AB、CD间的距离为h,在a、b、r、h这四个变量中已知三个量可以求出另外一个量.
(2)在解无图题时,要考虑不同的情形,分情况讨论问题,此种类型题常因考虑不周而漏解.二、填空题(每小题4分,共12分)
4.工程上常用钢珠来测量零件上小孔
的直径,假设钢珠的直径是10mm,测
得钢珠顶端离零件表面的距离为8mm,
如图所示,则这个小孔的直径AB是_____mm.【解析】过O作OC⊥AB,垂足为C,连接OA,
则△AOC为直角三角形.
又OC=3mm,OA=5mm,
在Rt△AOC中,
由勾股定理,得
AC= =4(mm).
由垂径定理,得AC=BC,∴AB=2AC=8mm.
答案:85.如图,点A、B是⊙O上的两点,AB=10,点P是⊙O上的动点(P与A、B不重合),连接AP、PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF=_____.
【解析】∵OE⊥AP,∴AE=PE,
同理:BF=PF,∴EF= AB=5.
答案:56.如图,⊙O的弦BA的延长线与半径OC
的延长线交于点P,且PA=AB=6 cm,
PO=12 cm,则⊙O的半径为_____.【解析】过O点作OD⊥AB于D,则BD=AD=3 cm,
∴PD=6+3=9 cm,
在Rt△PDO中
在Rt△ODB中,
答案: cm三、解答题(共26分)
7.(8分)(2010·长春中考)如图,
将一个两边都带有刻度的直尺放在半
圆形纸片上,使其一边经过圆心O,
另一边所在直线与半圆相交于点D、E,量出半径OC=5 cm,弦DE=8 cm.求直尺的宽.【解析】过点O作OM⊥DE于点M,连接OD.
∴DM= DE.
∵DE=8,∴DM=4.
在Rt△ODM中,∵OD=OC=5,
∴OM=
∴直尺的宽度为3 cm.8.(8分)已知正方形ABCD和矩形EFGH按如图位置摆放,且AD=EH=2,EF=4,一圆过A、B、F、E四点,求该圆半径的长. 【解析】记圆心为O点,并设⊙O的半径为r.对于AB、EF的中点M、N,连接MN、BO、FO,
由对称性可知:MN过圆心O点,且MN⊥AB,MN⊥EF,
∵AD=EH=2,EF=4,
∴BM=1,
NF=2,OF=OB=r,在Rt△OBM中,MB2+OM2=OB2=r2,即1+OM2=r2,
在Rt△OFN中,NF2+ON2=OF2=r2,即4+ON2=r2,
∴1+OM2=4+ON2,
又∵MN=4,∴1+(4-ON)2=4+ON2,
解得:ON= ,
把ON= 代入4+ON2=r2,得:
r2=4+( )2= ,∴r= ,
∴该圆的半径长为 .【拓展延伸】
9.(10分)有一座圆弧形的拱桥,桥下水平面宽7.2 m,拱顶高出水面2.4 m,现有一货船宽3 m,船舱顶部为长方体,高出水面2 m,问该货船能否顺利通过这座拱桥?【解析】如图所示, 表示桥拱,
AB=7.2 m,CD=2.4 m,EF=3 m,D为AB、
EF的中点,且CD、NF、ME均垂直于AB,
设 所在圆的圆心为O,连接OA及ON,连接OD,则C、D、O
共线.设OA=R m,
则OD=OC-DC=(R-2.4)m,
AD= AB=3.6 m,
由勾股定理有OA2=AD2+OD2,
即R2=3.62+(R-2.4)2,解得R=3.9(m).货船能否顺利通过该桥,关键是看货箱顶部两角(M、N)是
否被桥拱( )拦住,即当货船位于桥下正中位置时,货
箱顶部两角(M、N)到水平面(AB)的高度是否小于FN.
在Rt△ONG中,
所以FN=DG=OG-OD=OG-(OC-DC)
=3.6-(3.9-2.4)=2.1(m).
因为2<2.1,所以货船可以顺利通过该桥.
同课章节目录
