24.1.3弧、弦、圆心角
文档属性
| 名称 | 24.1.3弧、弦、圆心角 |
|
|
| 格式 | zip | ||
| 文件大小 | 1008.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-24 11:48:57 | ||
图片预览










文档简介
课件46张PPT。 掌握圆心角、弧、弦之间的“等对等关系”的定理,并熟练运用其证明线段、角的相等问题.在应用时要注意不能忽略“在同圆或等圆中”这一前提条件. 圆的对称性及弧、弦、圆心角之间的对应关系
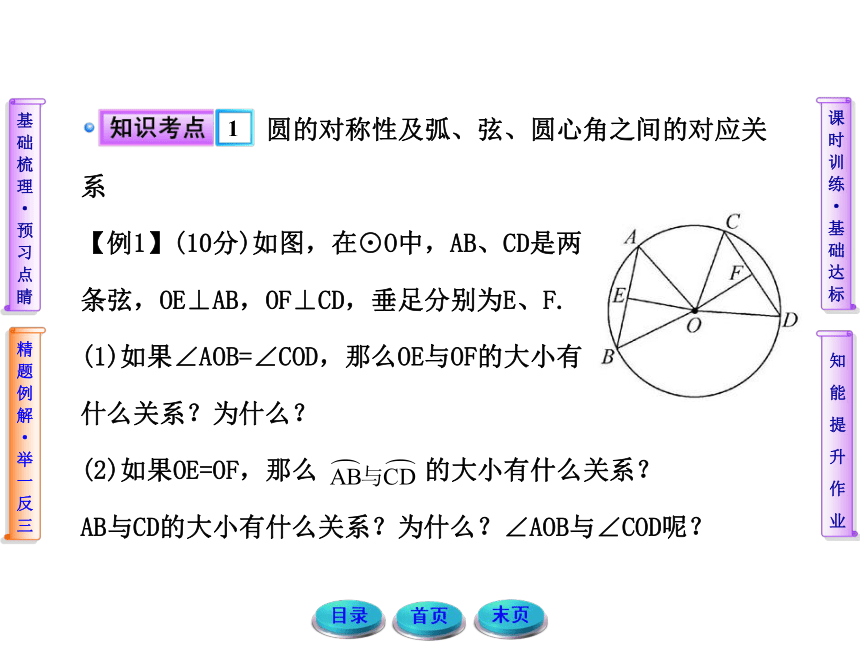
【例1】(10分)如图,在⊙O中,AB、CD是两
条弦,OE⊥AB,OF⊥CD,垂足分别为E、F.
(1)如果∠AOB=∠COD,那么OE与OF的大小有
什么关系?为什么?
(2)如果OE=OF,那么 的大小有什么关系?
AB与CD的大小有什么关系?为什么?∠AOB与∠COD呢?【规范解答】(1)如果∠AOB=∠COD,那么OE=OF.………2分
理由是:
∵∠AOB=∠COD,∴AB=CD.
∵OE⊥AB,OF⊥CD,∴AE= AB,CF= CD,∴AE=CF.…3分
又∵OA=OC,∴Rt△OEA≌Rt△OFC,
∴OE=OF.……………………………………………………5分(2)如果OE=OF,那么AB=CD, ,
∠AOB=∠COD.…………………………………………7分
理由是:∵OA=OC,OE=OF,
∴Rt△OEA≌Rt△OFC,∴AE=CF.……………………8分
又∵OE⊥AB,OF⊥CD,
∴AE= AB,CF= CD,∴AB=2AE,CD=2CF,
∴AB=CD.∴ ,∠AOB=∠COD.………………10分 理解弧、弦、圆心角之间的对应关系时,要明确由已知条件能得到哪些结论.同时要注意不是定理所涉及到的内容不能直接应用. 1.圆心角、弧、弦之间的相等关系是建立在“同圆或等圆”的
基础之上的,与之相关的辨析问题要特别注意;但是当已知弧
相等时,可以不另外说明“在同圆或等圆中”这一前提条件,
因为只有“在同圆或等圆中”,才有等弧的存在.
2.在同圆或等圆中,两条弦相等,那么圆心到这两条弦的距离
也相等.
3.由弦的相等推导所对应的弧相等时,必须同为优弧或同为劣
弧;由弦之间的倍数关系不能得到弧之间相对应的倍数关系. 1.如果两个圆心角相等,那么( )
(A)这两个圆心角所对的弦相等
(B)这两个圆心角所对的弧相等
(C)圆心到这两个圆心角所对的弦的距离相等
(D)以上说法都不对
【解析】选D.若不在同圆或等圆中,则A、B、C三个结论都不成立,故选D.2.(2010·宁波中考)下列各图是选自历届世博会会徽中的图案,其中是中心对称图形的是( )
【解析】选C.圆是中心对称图形.3.如图,CD为半圆上的三等分点,则下列
说法正确的是_____.
①弧AD、弧CD、弧BC相等;
②∠AOD=∠DOC=∠BOC;③AD=CD=OC;
④△AOD沿OD翻折与△COD重合.
【解析】根据弧、弦、圆心角之间的对应相等关系及轴对称的性质可以判断上述结论全部正确.
答案:①②③④ 1.圆既是轴对称图形又是中心对称图形,还具有旋转不变性.
2.判断弧、弦、圆心角之间的关系时要注意定理成立的前提条件,不可盲目作出判断. 弧、弦、圆心角关系定理的应用
【例2】如图所示,以□ABCD的顶点
A为圆心,AB为半径作⊙O,交AD、BC
于E、F,延长BA交⊙A于G,
求证:【思路点拨】 【自主解答】如图,连接AF,∵AB=AF,
∴∠B=∠AFB,
∵在? ABCD中,AD∥BC,
∴∠GAE=∠B,∠EAF=∠AFB,
∴∠GAE=∠EAF,∴ 弧、弦、圆心角之间的“等对等”关系是沟通圆的几个重要元素之间的桥梁,在证明线段、角的相等,角度的计算等问题上有重要的作用.证明两弧相等时,常用的方法是找这两弧所对的圆心角或弦相等.在应用时,要结合题意,灵活构造. 4.如图,已知AB是⊙O的直径,点C,D是 上的三等分
点,∠AOE=60°,则∠COE等于( )
(A)40° (B)65° (C)80° (D)120°
【解析】选C.∵AB是⊙O的直径,∠AOE=60°,
∴∠BOE=120°,又∵C、D是 上的三等分
点,
∴∠EOD=∠DOC=∠COB= ×120°=40°,∴∠COE=80°.5.如图,A、B、C为⊙O上的三点,且AO⊥BC,
则 ,若∠B=50°,则∠A的度数
是_____.
【解析】由垂径定理得, ,∴AB=AC,∴∠B=∠C,
∴∠A=180°-50°×2=80°.
答案:= 80° 在计算或证明中,要认真分析题意,根据“等对等”关系,进行恰当的构造和转换.涉及到垂径定理的图形结构时,要注意垂径定理的结论所提供的弧或线段的相等关系.1.下列图形是圆心角的是( )
【解析】选A.理解圆心角的概念要明确:①圆心角的特征:顶点与圆心重合,角的两边是圆的半径所在的射线;②圆心角具有角的一切性质和特征.2.在圆O上有顺次三点A、B、C,若 ,那么△ABC的形状是_____.
【解析】由弧的相等得到:AB=BC=CA ,故三角形为等边三角形.
答案:等边三角形3.如图,AB、CE是⊙O的直径,∠COD=60°,
且 ,那么与∠AOE相等的角有_____
(写出名称),与∠AOC相等的角有_____(写出
名称).【解析】∵ ,∴∠AOD=∠BOC.
又∵∠COD=60°,∴∠AOD=∠BOC=∠AOE=60°,∴与∠AOE相等的角有∠AOD、∠DOC、∠BOC;
与∠AOC相等的角有∠DOB、∠DOE、∠BOE.
答案:∠AOD、∠DOC、∠BOC
∠DOB、∠DOE、∠BOE4.如图所示,OA,OB,OC是⊙O的三条半径,
∠MCO=∠NCO,求证:AM=BN.
【证明】因为
所以∠AOC=∠BOC,
即∠COM=∠CON.
又因为∠MCO=∠NCO,OC=OC,
所以△COM≌△CON,所以OM=ON.
因为OA=OB,所以OA-OM=OB-ON,
即AM=BN.一、选择题(每小题4分,共12分)
1.如图,AC是⊙O的直径,AB、CD是⊙O的两
条弦,且AB∥CD,E为弧AD的中点,若
∠BAC=52°,则∠AOE的度数为( )
(A)26° (B)52°
(C)78° (D)104°【解析】选B.∵AB∥CD,∴∠C=∠BAC=52°,
又∵OC=OD,∴∠AOD=2∠C=104°,
又∵E为弧AD的中点,∴∠AOE=∠DOE=52°.2.已知,如图,在△ABC中,∠A=70°,⊙O截
△ABC的三边所得的弦长相等,则∠BOC=( )
(A)140° (B)135°
(C)130° (D)125°
【解析】选D.由题意知,圆心到三条弦的距离相等,所以O
在∠ABC与∠ACB的角平分线上,所以∠BOC=180°-
(∠ABC+∠ACB)=90°+ ∠A=125°. 【知识拓展】在同圆或等圆中,如果两条弦相等,那么圆心到这两条弦的距离也相等,反之也成立.3.A、B、C、D是⊙O上四点,且 ,则弦AB与弦CD的关系是( )
(A)AB >2CD (B)AB=2CD
(C)AB<2CD (D)不能确定
【解析】选C.取 的中点E,则 ,又∵ ,∴
∴AE=BE=CD,
又∵AE+BE>AB,∴2CD>AB.二、填空题(每小题4分,共12分)
4.如图,在⊙O中,AB=BC,且
=3∶4,则∠AOC=____.
【解析】∵AB=BC,∴
又∵ =3∶4,
∴∠AOC=360°× =144°.
答案:144°5.如图,若AB和DE是⊙O的直径,弦AC∥DE,
若弦BE=3,则弦CE=_____.
【解析】连接CO.∵AO=CO,
∴∠A=∠ACO,
又∵AC∥DE,∴∠ACO=∠COE,
∠A=∠EOB,∴∠COE=∠EOB,∴CE=BE=3.
答案:36.已知如图所示,A,B,C是⊙O上三点,
∠AOB=120°,C是 的中点,则四边形
OACB的形状是_____.【解析】连接OC,因为C是 的中点,所以∠AOC=∠BOC=
×120°=60°,又因为CO=BO,所以△OBC是等边三角
形,∴OB=BC,同理△OCA是等边三角形,∴OA=AC,又
∵OA=OB,∴OA=AC=BC=BO,所以四边形AOBC是菱形.
答案:菱形三、解答题(共26分)
7.(8分)如图,∠AOB=90°,C、D是 的
三等分点,AB分别交OC、OD于点E、F,求证:
AE=BF=CD.【证明】连接AC、BD,∵C、D是 的三等分点,∴AC=CD=DB,且∠AOC= ×90°=30°,
∵OA=OC,∴∠OAC=∠OCA=75°,
又∠AEC=∠OAE+∠AOE=45°+30°=75°,
∴AE=AC,
同理可证BF=BD,∴AE=BF=CD.8.(8分)如图1和图2,MN是
⊙O的直径,弦AB、CD相交于
MN上的一点P,∠APM=∠CPM.
(1)由以上条件,你认为AB
和CD大小关系是什么,请说明理由.
(2)若交点P在⊙O的外部,上述结论是否成立?若成立,加以证明;若不成立,请说明理由.【解析】(1)AB=CD
理由:过O作OE、OF分别垂直于AB、CD,垂足分别为E、F,
∵∠APM=∠CPM,∴∠1=∠2,OE=OF.
连接OD、OB且OB=OD
∴Rt△OFD≌Rt△OEB,∴DF=BE,
根据垂径定理可得:AB=CD.(2)作OE⊥AB,OF⊥CD,垂足分别为E、F
∵∠APM=∠CPN且OP=OP,∠PEO=∠PFO=90°,
∴Rt△OPE≌Rt△OPF,∴OE=OF,
连接OA、OB、OC、OD,
易证Rt△OBE≌Rt△ODF,Rt△OAE≌Rt△OCF,
∴∠1+∠2=∠3+∠4,∴AB=CD. 【归纳整合】弧、弦、圆心角之间的关系,给我们提供了研究线段相等、角相等、弧相等的依据和方法.有时结合垂径定理,提供弧的相等,进而得到弦或角的相等,在应用时要灵活把握.【拓展延伸】
9.(10分)如图,在⊙O中,C、D是直径AB
上两点,且AC=BD,MC⊥AB于C,ND⊥AB于D,
M、N在⊙O上.
(1)求证:
(2)若C、D分别为OA、OB的中点,则 成立
吗?【解析】(1)连接OM、ON,在Rt△OCM和Rt△ODN中,
OM=ON,∵OA=OB,AC=BD,
∴OC=OD,
∴Rt△OCM≌Rt△ODN,
∴∠AOM=∠BON,∴(2) 成立.
理由为:连接AM、BN.
∵AC=OC,MC⊥AB,∴MC垂直平分AO.
∴AM=OM. 同理:ON=BN.
∵OM=ON=OA=OB,
∴△AOM,△BON是等边三角形,
∴∠AOM=∠BON=60°,
∴∠MON=180°-∠AOM-∠BON=60°,
∴∠AOM=∠BON=∠MON.∴ .
【例1】(10分)如图,在⊙O中,AB、CD是两
条弦,OE⊥AB,OF⊥CD,垂足分别为E、F.
(1)如果∠AOB=∠COD,那么OE与OF的大小有
什么关系?为什么?
(2)如果OE=OF,那么 的大小有什么关系?
AB与CD的大小有什么关系?为什么?∠AOB与∠COD呢?【规范解答】(1)如果∠AOB=∠COD,那么OE=OF.………2分
理由是:
∵∠AOB=∠COD,∴AB=CD.
∵OE⊥AB,OF⊥CD,∴AE= AB,CF= CD,∴AE=CF.…3分
又∵OA=OC,∴Rt△OEA≌Rt△OFC,
∴OE=OF.……………………………………………………5分(2)如果OE=OF,那么AB=CD, ,
∠AOB=∠COD.…………………………………………7分
理由是:∵OA=OC,OE=OF,
∴Rt△OEA≌Rt△OFC,∴AE=CF.……………………8分
又∵OE⊥AB,OF⊥CD,
∴AE= AB,CF= CD,∴AB=2AE,CD=2CF,
∴AB=CD.∴ ,∠AOB=∠COD.………………10分 理解弧、弦、圆心角之间的对应关系时,要明确由已知条件能得到哪些结论.同时要注意不是定理所涉及到的内容不能直接应用. 1.圆心角、弧、弦之间的相等关系是建立在“同圆或等圆”的
基础之上的,与之相关的辨析问题要特别注意;但是当已知弧
相等时,可以不另外说明“在同圆或等圆中”这一前提条件,
因为只有“在同圆或等圆中”,才有等弧的存在.
2.在同圆或等圆中,两条弦相等,那么圆心到这两条弦的距离
也相等.
3.由弦的相等推导所对应的弧相等时,必须同为优弧或同为劣
弧;由弦之间的倍数关系不能得到弧之间相对应的倍数关系. 1.如果两个圆心角相等,那么( )
(A)这两个圆心角所对的弦相等
(B)这两个圆心角所对的弧相等
(C)圆心到这两个圆心角所对的弦的距离相等
(D)以上说法都不对
【解析】选D.若不在同圆或等圆中,则A、B、C三个结论都不成立,故选D.2.(2010·宁波中考)下列各图是选自历届世博会会徽中的图案,其中是中心对称图形的是( )
【解析】选C.圆是中心对称图形.3.如图,CD为半圆上的三等分点,则下列
说法正确的是_____.
①弧AD、弧CD、弧BC相等;
②∠AOD=∠DOC=∠BOC;③AD=CD=OC;
④△AOD沿OD翻折与△COD重合.
【解析】根据弧、弦、圆心角之间的对应相等关系及轴对称的性质可以判断上述结论全部正确.
答案:①②③④ 1.圆既是轴对称图形又是中心对称图形,还具有旋转不变性.
2.判断弧、弦、圆心角之间的关系时要注意定理成立的前提条件,不可盲目作出判断. 弧、弦、圆心角关系定理的应用
【例2】如图所示,以□ABCD的顶点
A为圆心,AB为半径作⊙O,交AD、BC
于E、F,延长BA交⊙A于G,
求证:【思路点拨】 【自主解答】如图,连接AF,∵AB=AF,
∴∠B=∠AFB,
∵在? ABCD中,AD∥BC,
∴∠GAE=∠B,∠EAF=∠AFB,
∴∠GAE=∠EAF,∴ 弧、弦、圆心角之间的“等对等”关系是沟通圆的几个重要元素之间的桥梁,在证明线段、角的相等,角度的计算等问题上有重要的作用.证明两弧相等时,常用的方法是找这两弧所对的圆心角或弦相等.在应用时,要结合题意,灵活构造. 4.如图,已知AB是⊙O的直径,点C,D是 上的三等分
点,∠AOE=60°,则∠COE等于( )
(A)40° (B)65° (C)80° (D)120°
【解析】选C.∵AB是⊙O的直径,∠AOE=60°,
∴∠BOE=120°,又∵C、D是 上的三等分
点,
∴∠EOD=∠DOC=∠COB= ×120°=40°,∴∠COE=80°.5.如图,A、B、C为⊙O上的三点,且AO⊥BC,
则 ,若∠B=50°,则∠A的度数
是_____.
【解析】由垂径定理得, ,∴AB=AC,∴∠B=∠C,
∴∠A=180°-50°×2=80°.
答案:= 80° 在计算或证明中,要认真分析题意,根据“等对等”关系,进行恰当的构造和转换.涉及到垂径定理的图形结构时,要注意垂径定理的结论所提供的弧或线段的相等关系.1.下列图形是圆心角的是( )
【解析】选A.理解圆心角的概念要明确:①圆心角的特征:顶点与圆心重合,角的两边是圆的半径所在的射线;②圆心角具有角的一切性质和特征.2.在圆O上有顺次三点A、B、C,若 ,那么△ABC的形状是_____.
【解析】由弧的相等得到:AB=BC=CA ,故三角形为等边三角形.
答案:等边三角形3.如图,AB、CE是⊙O的直径,∠COD=60°,
且 ,那么与∠AOE相等的角有_____
(写出名称),与∠AOC相等的角有_____(写出
名称).【解析】∵ ,∴∠AOD=∠BOC.
又∵∠COD=60°,∴∠AOD=∠BOC=∠AOE=60°,∴与∠AOE相等的角有∠AOD、∠DOC、∠BOC;
与∠AOC相等的角有∠DOB、∠DOE、∠BOE.
答案:∠AOD、∠DOC、∠BOC
∠DOB、∠DOE、∠BOE4.如图所示,OA,OB,OC是⊙O的三条半径,
∠MCO=∠NCO,求证:AM=BN.
【证明】因为
所以∠AOC=∠BOC,
即∠COM=∠CON.
又因为∠MCO=∠NCO,OC=OC,
所以△COM≌△CON,所以OM=ON.
因为OA=OB,所以OA-OM=OB-ON,
即AM=BN.一、选择题(每小题4分,共12分)
1.如图,AC是⊙O的直径,AB、CD是⊙O的两
条弦,且AB∥CD,E为弧AD的中点,若
∠BAC=52°,则∠AOE的度数为( )
(A)26° (B)52°
(C)78° (D)104°【解析】选B.∵AB∥CD,∴∠C=∠BAC=52°,
又∵OC=OD,∴∠AOD=2∠C=104°,
又∵E为弧AD的中点,∴∠AOE=∠DOE=52°.2.已知,如图,在△ABC中,∠A=70°,⊙O截
△ABC的三边所得的弦长相等,则∠BOC=( )
(A)140° (B)135°
(C)130° (D)125°
【解析】选D.由题意知,圆心到三条弦的距离相等,所以O
在∠ABC与∠ACB的角平分线上,所以∠BOC=180°-
(∠ABC+∠ACB)=90°+ ∠A=125°. 【知识拓展】在同圆或等圆中,如果两条弦相等,那么圆心到这两条弦的距离也相等,反之也成立.3.A、B、C、D是⊙O上四点,且 ,则弦AB与弦CD的关系是( )
(A)AB >2CD (B)AB=2CD
(C)AB<2CD (D)不能确定
【解析】选C.取 的中点E,则 ,又∵ ,∴
∴AE=BE=CD,
又∵AE+BE>AB,∴2CD>AB.二、填空题(每小题4分,共12分)
4.如图,在⊙O中,AB=BC,且
=3∶4,则∠AOC=____.
【解析】∵AB=BC,∴
又∵ =3∶4,
∴∠AOC=360°× =144°.
答案:144°5.如图,若AB和DE是⊙O的直径,弦AC∥DE,
若弦BE=3,则弦CE=_____.
【解析】连接CO.∵AO=CO,
∴∠A=∠ACO,
又∵AC∥DE,∴∠ACO=∠COE,
∠A=∠EOB,∴∠COE=∠EOB,∴CE=BE=3.
答案:36.已知如图所示,A,B,C是⊙O上三点,
∠AOB=120°,C是 的中点,则四边形
OACB的形状是_____.【解析】连接OC,因为C是 的中点,所以∠AOC=∠BOC=
×120°=60°,又因为CO=BO,所以△OBC是等边三角
形,∴OB=BC,同理△OCA是等边三角形,∴OA=AC,又
∵OA=OB,∴OA=AC=BC=BO,所以四边形AOBC是菱形.
答案:菱形三、解答题(共26分)
7.(8分)如图,∠AOB=90°,C、D是 的
三等分点,AB分别交OC、OD于点E、F,求证:
AE=BF=CD.【证明】连接AC、BD,∵C、D是 的三等分点,∴AC=CD=DB,且∠AOC= ×90°=30°,
∵OA=OC,∴∠OAC=∠OCA=75°,
又∠AEC=∠OAE+∠AOE=45°+30°=75°,
∴AE=AC,
同理可证BF=BD,∴AE=BF=CD.8.(8分)如图1和图2,MN是
⊙O的直径,弦AB、CD相交于
MN上的一点P,∠APM=∠CPM.
(1)由以上条件,你认为AB
和CD大小关系是什么,请说明理由.
(2)若交点P在⊙O的外部,上述结论是否成立?若成立,加以证明;若不成立,请说明理由.【解析】(1)AB=CD
理由:过O作OE、OF分别垂直于AB、CD,垂足分别为E、F,
∵∠APM=∠CPM,∴∠1=∠2,OE=OF.
连接OD、OB且OB=OD
∴Rt△OFD≌Rt△OEB,∴DF=BE,
根据垂径定理可得:AB=CD.(2)作OE⊥AB,OF⊥CD,垂足分别为E、F
∵∠APM=∠CPN且OP=OP,∠PEO=∠PFO=90°,
∴Rt△OPE≌Rt△OPF,∴OE=OF,
连接OA、OB、OC、OD,
易证Rt△OBE≌Rt△ODF,Rt△OAE≌Rt△OCF,
∴∠1+∠2=∠3+∠4,∴AB=CD. 【归纳整合】弧、弦、圆心角之间的关系,给我们提供了研究线段相等、角相等、弧相等的依据和方法.有时结合垂径定理,提供弧的相等,进而得到弦或角的相等,在应用时要灵活把握.【拓展延伸】
9.(10分)如图,在⊙O中,C、D是直径AB
上两点,且AC=BD,MC⊥AB于C,ND⊥AB于D,
M、N在⊙O上.
(1)求证:
(2)若C、D分别为OA、OB的中点,则 成立
吗?【解析】(1)连接OM、ON,在Rt△OCM和Rt△ODN中,
OM=ON,∵OA=OB,AC=BD,
∴OC=OD,
∴Rt△OCM≌Rt△ODN,
∴∠AOM=∠BON,∴(2) 成立.
理由为:连接AM、BN.
∵AC=OC,MC⊥AB,∴MC垂直平分AO.
∴AM=OM. 同理:ON=BN.
∵OM=ON=OA=OB,
∴△AOM,△BON是等边三角形,
∴∠AOM=∠BON=60°,
∴∠MON=180°-∠AOM-∠BON=60°,
∴∠AOM=∠BON=∠MON.∴ .
同课章节目录
