山东省德州市夏津县第一高级中学2022届高三12月月考数学试卷(PDF版含答案)
文档属性
| 名称 | 山东省德州市夏津县第一高级中学2022届高三12月月考数学试卷(PDF版含答案) |  | |
| 格式 | |||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-18 20:08:32 | ||
图片预览



文档简介
2019 级高三上学期 12 月月考数学试题
一、选择题 (本题共 8 小题, 每小题 5 分.在每小题给出的四个选项中, 只有 一
项符合题目要求)
1.已知集合 = { | = + }, = { | < },则 ∩ = ( )
A. ( , ) B. ( , ) C. ( , + ∞)D. ( , + ∞)
2.已知 2+i是关于 x的方程 x2 ax 5 0的根,则实数 a=( )
A.2-i B.-4 C.2 D.4
3.已知两条直线 :( + ) + = , : + ( + ) = , // ,则 = ( )
A. 或 B. C. D.
4.若 , , 是三个互不重合的平面,l是一条直线,则下列命题中正确的是( )
A. 若 ⊥ , ⊥ ,则 // B. 若 ⊥ , // ,则 ⊥
C. 若 l与 , 的所成角相等,则 // D. 若 l上有两个点到 的距离相等,则 //
5.若圆 x2+y2=r2(r>0)上恒有 4个点到直线 l:x-y-2=0的距离为 1,则实数 r的取
值范围是( )
A.( 2+1,+∞) B.( 2-1, 2+1) C.(0, 2-1) D.(0, 2+1)
6.若函数 = ( > )在[
, ]
上的最小值是 ,但最大值不是 2,则 的取
值范围是( )
A. ( , ) B. [ , ) C. ( , ] D. [ , + ∞)
2
7.直线 l:x-y=0 x与椭圆 +y2=1相交于 A、B两点,点 C是椭圆上的动点,则△ABC
2
面积的最大值为( )
A.1 B. 2 C. 3 D. 6
8.若不等式 ≤ ( + )对 ∈ ( , ]恒成立,则实数 a的取值范围是
( )
A. [ , + ∞) B. [ , + ∞) C. [ , + ∞) D. [ , + ∞)
1
二、选择题(本题共 4 小题, 每小题 5 分, 共 20 分。在每小题给出的选项中, 有多项符 合
要求。全部选对的得 5 分, 部分选对的得 2 分, 有选错的得 0 分)
9. 已知等比数列 an 中,满足 a1 1,公比 q=﹣2,则( )
A. 数列 2an an 1 是等比数列 B. 数列 an 1 an 是等比数列
C. 数列 anan 1 是等比数列 D. 数列 log2 an 是递减数列
10.在棱长为 2的正方体 ABCD A1B1C1D1 中,E,F ,G,H 分别为棱 A1D1 ,A1B1 ,B1C1 ,C1D1 的中点,将
该正方体挖去两个大小完全相同的四分之一圆锥,得到如图所示的几何体,则( )
A.CG / /平面 ADE
B.该几何体的上底面的周长为 4
2
C.该几何体的的体积为8
3
41
D.三棱锥F ABC 的外接球的表面积为 4
11. 将曲线 y sin2x 3sin x sin x
3
上每个点的横坐标伸长为原来的 2倍 (纵坐标
2
不变 ),得到 g x 的图象,则下列说法正确的是( )
3 3
A. g x 的图象关于直线 x 对称 B. g x 在 0, 上的值域为 0,
2 2
C. g x 的图象关于点 ,0 对称
6
D. g x 的图象可由 y cosx 1 2 的图象向右平移 个单位长度得到
2 3
12.用符号 x 表示不超过 x的最大整数,例如: 0.6 0, 2.3 2 .设
f (x) (1 ln x) ax 2 2ln x 有 3个不同的零点 x1, x2, x3,则( )
A. x e是 f (x)的一个零点 B. x1 x2 x3 2 e e
1 2ln3 ln 2
C. a的取值范围是 ,0 D.若 x1 x2 x3 6,则 a的范围是 , e . 9 4
2
三、填空题(本题共 4 小题, 每小题 5 分, 共 20 分)
13.在四边形 ABCD中,AD∥BC,AB=2 3,AD=5,∠A=30°,点 E在线段 CB的
→ →
延长线上,且 AE=BE,则BD·AE=________.
1
14.已知数列 an 的前 n项和 Sn满足 S n
2
n ,记数列 的前
n项和为Tn ,
ana
n 1
n N*.则使得T20 的值为________.
15.已知 ( + ) = + ,则 + + 的最小值为______.
x 4e, x 0
16.已知函数 f (x)
ex ,若存在 x 0,x 0,使得 f (x ) f (x ),则 x f (x )
, x 0
1 2 1 2 1 2
x
的取值范围是______.
四、解答题(本题共 6 小题, 共 70 分)
3
17.设△ 的内角A、B、C的对边长分别为 a、b、 .设 S为△ 的面积,满 S = (a 2 +c2 -b2 )
4
(1)求 B;
(2)若 = ,求( ) + 的最大值.
1
18.在①数列 an 2 *的前 项和 Sn n n, n N ;②数列 an 是首项为 1,公差不为 0的2
正项等差数列,且 a2 ,a ,a ,
a
成等比数列;③ a 1, n 1 n 1 *4 8 1 , n N 这三个条件中任选一an n
个,补充在下面的问题中,若问题中的m,k存在,求出m,k的值;若不存在,说明理由.
已知数列 an ,且__________,设b
a
nn ,是否存在正整数m,k 1 m k 使得ba a 1
,bm ,bk
n n 1
成等差数列
3
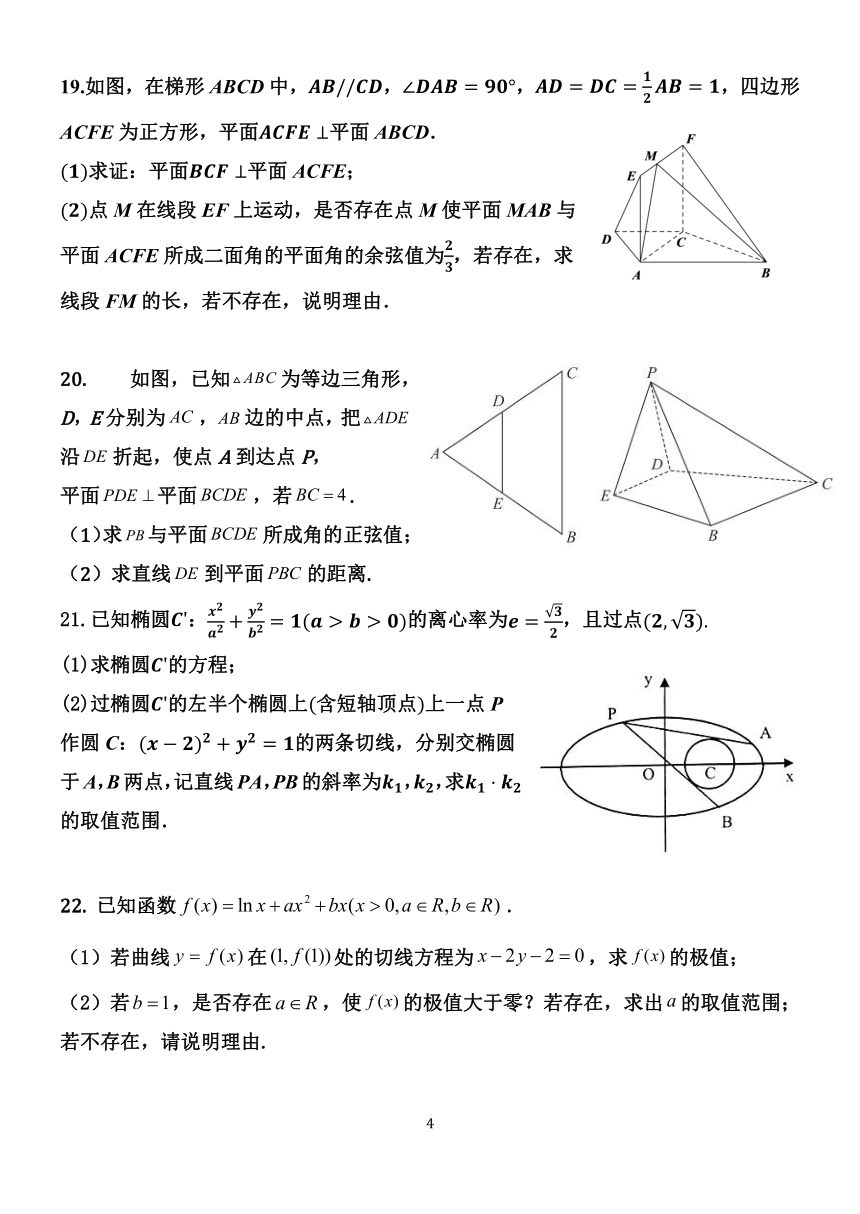
19.如图,在梯形 ABCD中, // ,∠ = °, = = = ,四边形
ACFE为正方形,平面 ⊥平面 ABCD.
( )求证:平面 ⊥平面 ACFE;
( )点M在线段 EF上运动,是否存在点M使平面MAB与
平面 ACFE 所成二面角的平面角的余弦值为 ,若存在,求
线段 FM的长,若不存在,说明理由.
20. 如图,已知 ABC为等边三角形,
D,E分别为 AC ,AB边的中点,把 ADE
沿DE 折起,使点 A到达点 P,
平面 PDE 平面 BCDE ,若 BC 4 .
(1)求 PB与平面BCDE 所成角的正弦值;
(2)求直线DE 到平面PBC 的距离.
21.已知椭圆 ': + = ( > > )的离心率为 = ,且过点( , ).
(1)求椭圆 '的方程;
(2)过椭圆 '的左半个椭圆上(含短轴顶点)上一点 P
作圆 C:( ) + = 的两条切线,分别交椭圆
于A,B两点,记直线PA,PB的斜率为 , ,求
的取值范围.
22. 已知函数 f (x) ln x ax 2 bx(x 0,a R,b R) .
(1)若曲线 y f (x)在 (1, f (1))处的切线方程为 x 2y 2 0,求 f (x)的极值;
(2)若b 1,是否存在a R,使 f (x)的极值大于零?若存在,求出 a的取值范围;
若不存在,请说明理由.
4
月考参考答案:1-4 ABCB 5-8 A BBD 9.BC 10.ABD 11. BD 12.AD
20
13.-1 14. 15. ( + ) 16. 4e
2 ,0
41
17.解:(1) ;
(2 , ,由正弦定理知 ,
,
= + = ( + ) ≤ =
,当且仅当 时取最大值,
故( ) + 的最大值为 .
18..答案:若选①,当 时, ,
当 时, ,满足上式,故 ,所以 .
设存在正整数 使得 成等差数列,
则 ,即 ,
即 ,即 ,即 .
由 ,且 可得 是奇数,所以 (舍去)或 ,所以 ,
故存在 使得 成等差数列.若选②,由 成等比数列,可得 ,
设数列 的公差为 ,则 ,可得 ,
所以 ,所以 .假设存在正整数 使得 成等差数列,
则 ,即 ,即 ,
即 ,即 .由 ,且 可得 是奇数,
所以 (舍去)或 ,所以 ,故存在 使得 成等差数列.
5
若选③,因为 ,所以
,即
,所以 .假设存在正整数 使得 成等差数列,
则 ,即 ,即 ,
即 ,即 .由 ,且 可得 是奇数,
所以 (舍去)或 ,所以 ,故存在 使得 成等差数列.
19.( )证明:在梯形 ABCD中,因为 // , = = ,∠ = ,所以 = ,
又因为 = ,取 AB中点 P,连接 PC,则 , = ,易知 = ,
所以 = + ,所以 ⊥ .因为平面 ⊥平面 ABCD,平面 ∩平
面 = , 平面ABCD所以 ⊥平面ACFE,又 平面BCF.
所以平面 ⊥平面 ACFE;
( )由( )可建立分别以直线 CA,CB,CF为 x轴,y轴,z轴的
如图所示空间直角坐标系,令 = ≤ ≤ ,
则 , , , , , , , , , , ,
→ → →
所以 = , , , = , , 设 = , , 为平面MAB的一个法向量,
��� �· ��� �� = + = →由 得 取 = ,则 = , , ,
� �� �· ��� ��� = + =
→ |� �� � ��� �|
因为 = , , 是平面 ACFE的一个法向量所以
= = =
| ��� �| | ��� �| + +( ) ×
=
可得( ) + =
,即 = .
20.(1)如图所示,
设DE 的中点为 O,BC的中点为 F,连接OP,OF ,OB,
则OP DE .因为平面 PDE 平面BCDE ,
平面PDE 平面 BCDE DE ,
6
所以OP 平面 BCDE .因为OB 平面 BCDE ,所以OP OB,
所以 OBP即为直线 PB与平面BCDE所成的角.因为BC 4
1
,则DE BC 2,
2
所以OP OF 3 .在Rt△OBF 中, BF 2 ,OF BF ,所以OB 7 .
在Rt△OBP中, PB OP2 OB2 3 7 10 ,所以 sin OBP
OP 3 30
.
PB 10 10
(2)解法一:因为点 D,E分别为 AC ,AB边的中点,所以DE//BC .
因为DE 平面 PBC , BC 平面PBC ,所以DE//平面PBC .
由(1)知,OP 平面 BCDE ,又OF DE,所以以点 O为坐标
原点,OE,OF ,OP所在直线为 x,y,z轴建立如图所示的空
间直角坐标系,
则O 0,0,0 ,P 0,0, 3 ,B 2, 3,0 ,C 2, 3,0 ,F 0, 3,0 ,
uur
所以 PB 2, 3, 3 ,CB 4,0,0 .设平面 PBC 的一个法向量为 n x, y, z ,
n P B 2x 3 y 3z 0,
x 0, r
由 得 令 y z 1,所以 n 0,1,1 .
n CB 4x 0 y z,
uuur r
uuur OF n 3 6
因为OF 0, 3,0 ,设点 O到平面 PBC 的距离为 d,则 d r 2 .n 2
O DE DE PBC 6因为点 在直线 上,所以直线 到平面 的距离等于 .
2
21 解:(Ⅰ) 由题意可得 = = = ,即 = ,
+ = = = +
又 ,解得 , ,则椭圆的方程为 ; =
(Ⅱ)设 ( , ),( ≤ ≤ ) ,则 + = 即 = ,
设过 P的切线方程为 = + ,圆 C:( ) + = 的圆心为( , ),半径为 1,
| + |
由直线和圆相切的条件可得 = ,化为( + ) + ( ) + = , +
由 , 为上面方程的两根,可得 =
=
+ +
7
= ( ≤ ≤ ),令 = ( ≤ ≤ )
+
,则 = ,
+
则 =
( +
=
) +
+ + 在 ≤ ≤ 递增,
所以 的取值范围是[ , ].
f x 122.解:(1)依题意, 2ax b, f 1 1 2a b,
x
f 1 1 2a b 1 a 01 1 2
又由切线方程可知, f 1 ,斜率 k ,所以{ ,解得{ ,所
2 2 f 1 a b 1
1
b
2 2
f x lnx— x以 ,所以
2
f x 1 1 2 x (x 0),
x 2 2x
当 x 0时, x, f x , f x 的变化如下:所以
f x f 2 ln2 1,无极小值.
极大值
2
(2)依题意, f x lnx ax2 x f x 1 2ax 1 2ax x 1,所以 (x 0) ,
x x
①当 a 0时, f x 0在 0, 上恒成立,故无极值;
1
②当 a 0时,令 f x 0,得 2ax2 x 1 0,则 1 8a 0,且两根之积 x1x2 0,2a
x 0, x 2a x x1 x x2 不妨设 1 2 0,则 f x ,即求使 f x2 0的实数 a的取值范围.x
2ax2
{ 2
x2 1 0 x 1
由方程组 2 消去参数 a后,得 lnx
2
2 0,lnx2 ax2 x2 0 2
x 1
构造函数 g x lnx ,则 g x 1 1 0,所以 g x 在 0, 上单调递增,
2 x 2
又 g 1 0,所以 g x 0 1 1 8a解得 x 1,即 x2 1,解得 1 a 0 .4a
由①②可得, a的范围是 1 a 0 .
8
一、选择题 (本题共 8 小题, 每小题 5 分.在每小题给出的四个选项中, 只有 一
项符合题目要求)
1.已知集合 = { | = + }, = { | < },则 ∩ = ( )
A. ( , ) B. ( , ) C. ( , + ∞)D. ( , + ∞)
2.已知 2+i是关于 x的方程 x2 ax 5 0的根,则实数 a=( )
A.2-i B.-4 C.2 D.4
3.已知两条直线 :( + ) + = , : + ( + ) = , // ,则 = ( )
A. 或 B. C. D.
4.若 , , 是三个互不重合的平面,l是一条直线,则下列命题中正确的是( )
A. 若 ⊥ , ⊥ ,则 // B. 若 ⊥ , // ,则 ⊥
C. 若 l与 , 的所成角相等,则 // D. 若 l上有两个点到 的距离相等,则 //
5.若圆 x2+y2=r2(r>0)上恒有 4个点到直线 l:x-y-2=0的距离为 1,则实数 r的取
值范围是( )
A.( 2+1,+∞) B.( 2-1, 2+1) C.(0, 2-1) D.(0, 2+1)
6.若函数 = ( > )在[
, ]
上的最小值是 ,但最大值不是 2,则 的取
值范围是( )
A. ( , ) B. [ , ) C. ( , ] D. [ , + ∞)
2
7.直线 l:x-y=0 x与椭圆 +y2=1相交于 A、B两点,点 C是椭圆上的动点,则△ABC
2
面积的最大值为( )
A.1 B. 2 C. 3 D. 6
8.若不等式 ≤ ( + )对 ∈ ( , ]恒成立,则实数 a的取值范围是
( )
A. [ , + ∞) B. [ , + ∞) C. [ , + ∞) D. [ , + ∞)
1
二、选择题(本题共 4 小题, 每小题 5 分, 共 20 分。在每小题给出的选项中, 有多项符 合
要求。全部选对的得 5 分, 部分选对的得 2 分, 有选错的得 0 分)
9. 已知等比数列 an 中,满足 a1 1,公比 q=﹣2,则( )
A. 数列 2an an 1 是等比数列 B. 数列 an 1 an 是等比数列
C. 数列 anan 1 是等比数列 D. 数列 log2 an 是递减数列
10.在棱长为 2的正方体 ABCD A1B1C1D1 中,E,F ,G,H 分别为棱 A1D1 ,A1B1 ,B1C1 ,C1D1 的中点,将
该正方体挖去两个大小完全相同的四分之一圆锥,得到如图所示的几何体,则( )
A.CG / /平面 ADE
B.该几何体的上底面的周长为 4
2
C.该几何体的的体积为8
3
41
D.三棱锥F ABC 的外接球的表面积为 4
11. 将曲线 y sin2x 3sin x sin x
3
上每个点的横坐标伸长为原来的 2倍 (纵坐标
2
不变 ),得到 g x 的图象,则下列说法正确的是( )
3 3
A. g x 的图象关于直线 x 对称 B. g x 在 0, 上的值域为 0,
2 2
C. g x 的图象关于点 ,0 对称
6
D. g x 的图象可由 y cosx 1 2 的图象向右平移 个单位长度得到
2 3
12.用符号 x 表示不超过 x的最大整数,例如: 0.6 0, 2.3 2 .设
f (x) (1 ln x) ax 2 2ln x 有 3个不同的零点 x1, x2, x3,则( )
A. x e是 f (x)的一个零点 B. x1 x2 x3 2 e e
1 2ln3 ln 2
C. a的取值范围是 ,0 D.若 x1 x2 x3 6,则 a的范围是 , e . 9 4
2
三、填空题(本题共 4 小题, 每小题 5 分, 共 20 分)
13.在四边形 ABCD中,AD∥BC,AB=2 3,AD=5,∠A=30°,点 E在线段 CB的
→ →
延长线上,且 AE=BE,则BD·AE=________.
1
14.已知数列 an 的前 n项和 Sn满足 S n
2
n ,记数列 的前
n项和为Tn ,
ana
n 1
n N*.则使得T20 的值为________.
15.已知 ( + ) = + ,则 + + 的最小值为______.
x 4e, x 0
16.已知函数 f (x)
ex ,若存在 x 0,x 0,使得 f (x ) f (x ),则 x f (x )
, x 0
1 2 1 2 1 2
x
的取值范围是______.
四、解答题(本题共 6 小题, 共 70 分)
3
17.设△ 的内角A、B、C的对边长分别为 a、b、 .设 S为△ 的面积,满 S = (a 2 +c2 -b2 )
4
(1)求 B;
(2)若 = ,求( ) + 的最大值.
1
18.在①数列 an 2 *的前 项和 Sn n n, n N ;②数列 an 是首项为 1,公差不为 0的2
正项等差数列,且 a2 ,a ,a ,
a
成等比数列;③ a 1, n 1 n 1 *4 8 1 , n N 这三个条件中任选一an n
个,补充在下面的问题中,若问题中的m,k存在,求出m,k的值;若不存在,说明理由.
已知数列 an ,且__________,设b
a
nn ,是否存在正整数m,k 1 m k 使得ba a 1
,bm ,bk
n n 1
成等差数列
3
19.如图,在梯形 ABCD中, // ,∠ = °, = = = ,四边形
ACFE为正方形,平面 ⊥平面 ABCD.
( )求证:平面 ⊥平面 ACFE;
( )点M在线段 EF上运动,是否存在点M使平面MAB与
平面 ACFE 所成二面角的平面角的余弦值为 ,若存在,求
线段 FM的长,若不存在,说明理由.
20. 如图,已知 ABC为等边三角形,
D,E分别为 AC ,AB边的中点,把 ADE
沿DE 折起,使点 A到达点 P,
平面 PDE 平面 BCDE ,若 BC 4 .
(1)求 PB与平面BCDE 所成角的正弦值;
(2)求直线DE 到平面PBC 的距离.
21.已知椭圆 ': + = ( > > )的离心率为 = ,且过点( , ).
(1)求椭圆 '的方程;
(2)过椭圆 '的左半个椭圆上(含短轴顶点)上一点 P
作圆 C:( ) + = 的两条切线,分别交椭圆
于A,B两点,记直线PA,PB的斜率为 , ,求
的取值范围.
22. 已知函数 f (x) ln x ax 2 bx(x 0,a R,b R) .
(1)若曲线 y f (x)在 (1, f (1))处的切线方程为 x 2y 2 0,求 f (x)的极值;
(2)若b 1,是否存在a R,使 f (x)的极值大于零?若存在,求出 a的取值范围;
若不存在,请说明理由.
4
月考参考答案:1-4 ABCB 5-8 A BBD 9.BC 10.ABD 11. BD 12.AD
20
13.-1 14. 15. ( + ) 16. 4e
2 ,0
41
17.解:(1) ;
(2 , ,由正弦定理知 ,
,
= + = ( + ) ≤ =
,当且仅当 时取最大值,
故( ) + 的最大值为 .
18..答案:若选①,当 时, ,
当 时, ,满足上式,故 ,所以 .
设存在正整数 使得 成等差数列,
则 ,即 ,
即 ,即 ,即 .
由 ,且 可得 是奇数,所以 (舍去)或 ,所以 ,
故存在 使得 成等差数列.若选②,由 成等比数列,可得 ,
设数列 的公差为 ,则 ,可得 ,
所以 ,所以 .假设存在正整数 使得 成等差数列,
则 ,即 ,即 ,
即 ,即 .由 ,且 可得 是奇数,
所以 (舍去)或 ,所以 ,故存在 使得 成等差数列.
5
若选③,因为 ,所以
,即
,所以 .假设存在正整数 使得 成等差数列,
则 ,即 ,即 ,
即 ,即 .由 ,且 可得 是奇数,
所以 (舍去)或 ,所以 ,故存在 使得 成等差数列.
19.( )证明:在梯形 ABCD中,因为 // , = = ,∠ = ,所以 = ,
又因为 = ,取 AB中点 P,连接 PC,则 , = ,易知 = ,
所以 = + ,所以 ⊥ .因为平面 ⊥平面 ABCD,平面 ∩平
面 = , 平面ABCD所以 ⊥平面ACFE,又 平面BCF.
所以平面 ⊥平面 ACFE;
( )由( )可建立分别以直线 CA,CB,CF为 x轴,y轴,z轴的
如图所示空间直角坐标系,令 = ≤ ≤ ,
则 , , , , , , , , , , ,
→ → →
所以 = , , , = , , 设 = , , 为平面MAB的一个法向量,
��� �· ��� �� = + = →由 得 取 = ,则 = , , ,
� �� �· ��� ��� = + =
→ |� �� � ��� �|
因为 = , , 是平面 ACFE的一个法向量所以
= = =
| ��� �| | ��� �| + +( ) ×
=
可得( ) + =
,即 = .
20.(1)如图所示,
设DE 的中点为 O,BC的中点为 F,连接OP,OF ,OB,
则OP DE .因为平面 PDE 平面BCDE ,
平面PDE 平面 BCDE DE ,
6
所以OP 平面 BCDE .因为OB 平面 BCDE ,所以OP OB,
所以 OBP即为直线 PB与平面BCDE所成的角.因为BC 4
1
,则DE BC 2,
2
所以OP OF 3 .在Rt△OBF 中, BF 2 ,OF BF ,所以OB 7 .
在Rt△OBP中, PB OP2 OB2 3 7 10 ,所以 sin OBP
OP 3 30
.
PB 10 10
(2)解法一:因为点 D,E分别为 AC ,AB边的中点,所以DE//BC .
因为DE 平面 PBC , BC 平面PBC ,所以DE//平面PBC .
由(1)知,OP 平面 BCDE ,又OF DE,所以以点 O为坐标
原点,OE,OF ,OP所在直线为 x,y,z轴建立如图所示的空
间直角坐标系,
则O 0,0,0 ,P 0,0, 3 ,B 2, 3,0 ,C 2, 3,0 ,F 0, 3,0 ,
uur
所以 PB 2, 3, 3 ,CB 4,0,0 .设平面 PBC 的一个法向量为 n x, y, z ,
n P B 2x 3 y 3z 0,
x 0, r
由 得 令 y z 1,所以 n 0,1,1 .
n CB 4x 0 y z,
uuur r
uuur OF n 3 6
因为OF 0, 3,0 ,设点 O到平面 PBC 的距离为 d,则 d r 2 .n 2
O DE DE PBC 6因为点 在直线 上,所以直线 到平面 的距离等于 .
2
21 解:(Ⅰ) 由题意可得 = = = ,即 = ,
+ = = = +
又 ,解得 , ,则椭圆的方程为 ; =
(Ⅱ)设 ( , ),( ≤ ≤ ) ,则 + = 即 = ,
设过 P的切线方程为 = + ,圆 C:( ) + = 的圆心为( , ),半径为 1,
| + |
由直线和圆相切的条件可得 = ,化为( + ) + ( ) + = , +
由 , 为上面方程的两根,可得 =
=
+ +
7
= ( ≤ ≤ ),令 = ( ≤ ≤ )
+
,则 = ,
+
则 =
( +
=
) +
+ + 在 ≤ ≤ 递增,
所以 的取值范围是[ , ].
f x 122.解:(1)依题意, 2ax b, f 1 1 2a b,
x
f 1 1 2a b 1 a 01 1 2
又由切线方程可知, f 1 ,斜率 k ,所以{ ,解得{ ,所
2 2 f 1 a b 1
1
b
2 2
f x lnx— x以 ,所以
2
f x 1 1 2 x (x 0),
x 2 2x
当 x 0时, x, f x , f x 的变化如下:所以
f x f 2 ln2 1,无极小值.
极大值
2
(2)依题意, f x lnx ax2 x f x 1 2ax 1 2ax x 1,所以 (x 0) ,
x x
①当 a 0时, f x 0在 0, 上恒成立,故无极值;
1
②当 a 0时,令 f x 0,得 2ax2 x 1 0,则 1 8a 0,且两根之积 x1x2 0,2a
x 0, x 2a x x1 x x2 不妨设 1 2 0,则 f x ,即求使 f x2 0的实数 a的取值范围.x
2ax2
{ 2
x2 1 0 x 1
由方程组 2 消去参数 a后,得 lnx
2
2 0,lnx2 ax2 x2 0 2
x 1
构造函数 g x lnx ,则 g x 1 1 0,所以 g x 在 0, 上单调递增,
2 x 2
又 g 1 0,所以 g x 0 1 1 8a解得 x 1,即 x2 1,解得 1 a 0 .4a
由①②可得, a的范围是 1 a 0 .
8
同课章节目录
