广东省汕头市金山中学2013届高三上学期期中 数学理试题
文档属性
| 名称 | 广东省汕头市金山中学2013届高三上学期期中 数学理试题 |  | |
| 格式 | zip | ||
| 文件大小 | 232.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-24 13:58:19 | ||
图片预览




文档简介
汕头市金山中学2012-2013学年度第一学期期中考试
高三理科数学 试题卷
本试题分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,时间120分钟.
第Ⅰ卷 (选择题 共40分)
一、选择题:(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.等于( )
A. B. C. D.
2.设, 那么“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
3.已知单位向量满足,则夹角为( )
A. B. C. D.
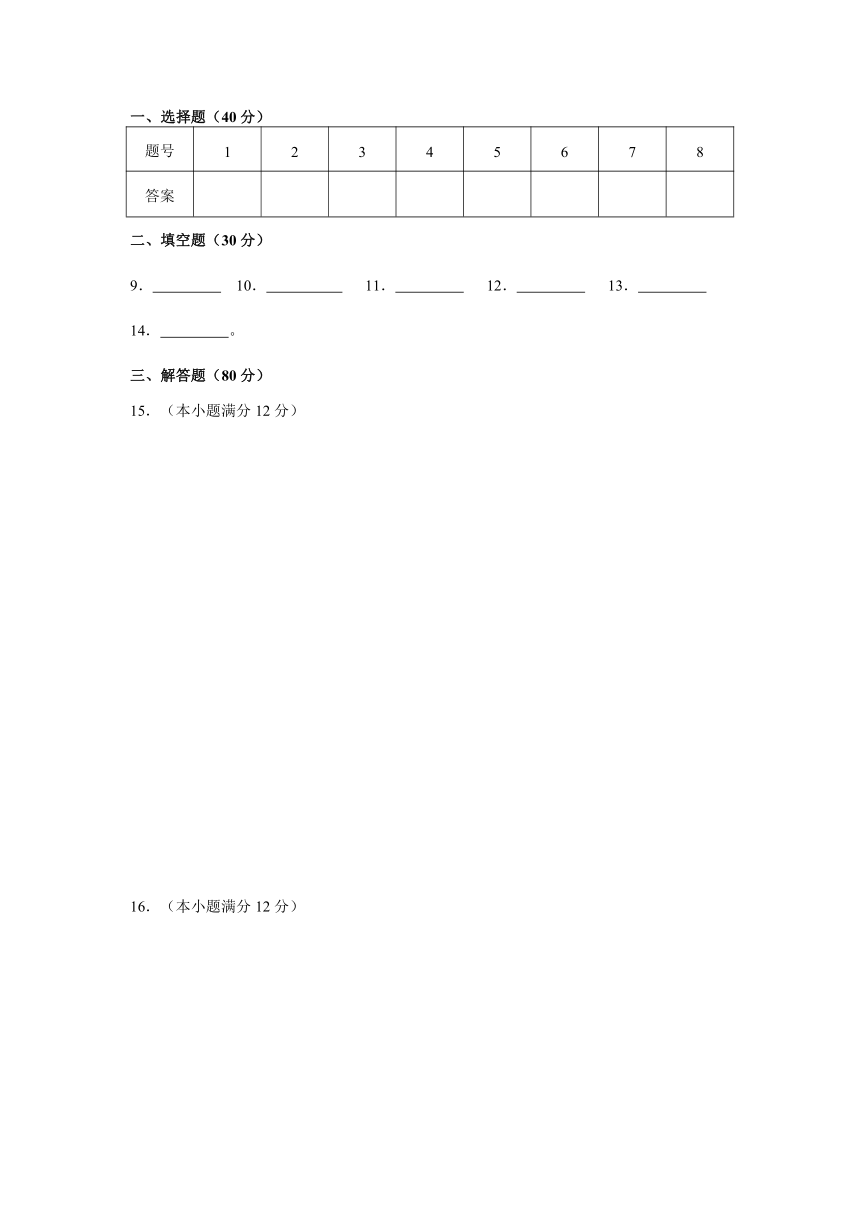
4.已知函数,且此函数的图象如图所示,则点的坐标是( )
A. B.
C. D.
5.函数的图象大致是( )
6.已知满足线性约束条件,若,,则的最大值是( )
A. B. C. D.
7.若函数的零点与函数的零点之差的绝对值不超过,则可以是( )
A. B. C. D.
8.对于下列命题:①在△ABC中,若,则△ABC为等腰三角形;②已知a,b,c是△ABC的三边长,若,,,则△ABC有两组解;③设,,,则;④将函数图象向左平移个单位,得到函数图象。其中正确命题的个数是( )
A. B. C. D.
第Ⅱ卷 (非选择题 共110分)
二、填空题:(本大题共6小题,每小题5分,共30分.) 21世纪教育网
9.已知向量,,.若为实数,,则 。
10.设 的最大值为16,则 。
11.已知,,则 。
12.在△中,内角、、的对边分别为、、,已知,,,则 。
13.若关于的不等式存在实数解,则实数的取值范围是 。
14.函数.给出函数下列性质:①函数的定义域和值域均为;②函数的图像关于原点成中心对称;③函数在定义域上单调递增;④(其中为函数的定义域);⑤、为函数图象上任意不同两点,则。请写出所有关于函数性质正确描述的序号 。
三、解答题:(本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤.)
15.(本小题满分12分)
已知集合,.
(Ⅰ)求集合和集合;
(Ⅱ)若,求的取值范围。
16.(本小题满分12分)
在直角坐标系中,已知,,为坐标原点,,.
(Ⅰ)求的对称中心的坐标及其在区间上的单调递减区间;
(Ⅱ)若,,求的值。
17.(本小题满分14分)21世纪教育网
已知函数,
(Ⅰ)求函数的最大值和最小正周期;
(Ⅱ)设的内角的对边分别且,,若,求的值.
18.(本小题满分14分)
已知函数,
(Ⅰ)若,求的单调区间;
(Ⅱ)在(Ⅰ)的条件下,对,都有,求实数的取值范围;
(Ⅲ)若在,上单调递增,在上单调递减,求实数的取值范围。
19.(本小题满分14分)
如图:某污水处理厂要在一个矩形污水处理池的池底水平铺设污水净化管道,是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口是的中点,分别落在线段上。已知米,米,记。
(Ⅰ)试将污水净化管道的长度表示为的函数,并写出定义域;
(Ⅱ)若,求此时管道的长度;
(Ⅲ)问:当取何值时,铺设管道的成本最低?并求出此时管道的长度。
20.(本小题满分14分)
已知函数的单调递增区间为,
(Ⅰ)求证:;
(Ⅱ)当取最小值时,点是函数图象上的两点,若存在使得,求证:
汕头市金山中学2012-2013学年度第一学期期中考试
高三理科数学 答题卷
班级 姓名 学号 评分
一、选择题(40分)
题号
1
2
3
4
5
6
7
8
答案
二、填空题(30分)
9. 10. 11. 12. 13.
14. 。
三、解答题(80分)
15.(本小题满分12分)
16.(本小题满分12分)
17.(本小题满分14分)
姓名 学号
18.(本小题满分14分)
19.(本小题满分14分)
21世纪教育网
20.(本小题满分14分)
汕头市金山中学2012-2013学年度第一学期期中考试
高三理科数学 参考答案
一、选择题(40分)
题号
1
2
3
4
5
6
7
8
答案
D
A
C
A
D
B
C
C
二、填空题(30分)
9. 10. 11. 12. 13. 14.②④
三、解答题(80分)
15.解:(Ⅰ)由,得,即…………………3分
由或,
即………………………………………………………………………6分
(Ⅱ),
的取值范围是…………………………………………………………………12分
16.解:,,
则……………21世纪教育网……………………2分
……………………………………………………4分
(Ⅰ)由,即对称中心是
当时单调递减,即
的单调递减是………………………………………6分
在区间上的单调递减区间为.………………………………………8分
(Ⅱ)
……………………………………10分
。…………………………………………………12分
17.解:(Ⅰ)…………………………2分
则的最大值为0,最小正周期是……………………………………………4分
(Ⅱ)则
……………………………………………………………………………6分
由正弦定理得①…………21世纪教育网…………………9分
由余弦定理得
即②……………………………………………………………………………12分
由①②解得,…………………………………………………………………14分
18.解:(Ⅰ)定义域为
当时,,,令得或(舍)
(0,2)
2
-
0
+
↘
↗
∴的递减区间为(0,2),递增区间为…………………………………………4分
(Ⅱ)∵都有成立
∴………………………………………………………………………………5分
由(Ⅰ)知
,……………………………………………7分
∴,∴……………………………………………………………………8分
(Ⅲ)…………………………………9分
由条件知恰为的两个不相等正根,
即恰有两个不相等正根,……………………………………………10分
对于方程显然是方程的一个解,……………………………11分
当时,(且)
当时,
当时,…………………………………………………………………13分
∴且…………………………………………21世纪教育网……………………14分
19.解:(Ⅰ),,
由于,,,。……3分
所以 ,………………………………………………5分
(Ⅱ)时,,;…………………………10分
(Ⅲ)=,设,
则,由于,
所以 ,在 内单调递减,
于是当时. 的最小值米……………………………………………13分
答:当时,所铺设管道的成本最低,此时管道的长度为米………………14分
20.解:(Ⅰ)……………………………………………………………2分
依题意是方程的两根有:………………………………4分
……………6分
(Ⅱ)
取最小值时,,……………………………………………………7分
在上是增函数,,
,从而………………………………………………8分
即
…………………21世纪教育网…………10分
考虑函数,因,故当时,有,
所以是上是减函数.
由,得………21世纪教育网…………………………12分
由及得
故,即.
……………………………………………21世纪教育网……………………………14分
高三理科数学 试题卷
本试题分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,时间120分钟.
第Ⅰ卷 (选择题 共40分)
一、选择题:(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.等于( )
A. B. C. D.
2.设, 那么“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
3.已知单位向量满足,则夹角为( )
A. B. C. D.
4.已知函数,且此函数的图象如图所示,则点的坐标是( )
A. B.
C. D.
5.函数的图象大致是( )
6.已知满足线性约束条件,若,,则的最大值是( )
A. B. C. D.
7.若函数的零点与函数的零点之差的绝对值不超过,则可以是( )
A. B. C. D.
8.对于下列命题:①在△ABC中,若,则△ABC为等腰三角形;②已知a,b,c是△ABC的三边长,若,,,则△ABC有两组解;③设,,,则;④将函数图象向左平移个单位,得到函数图象。其中正确命题的个数是( )
A. B. C. D.
第Ⅱ卷 (非选择题 共110分)
二、填空题:(本大题共6小题,每小题5分,共30分.) 21世纪教育网
9.已知向量,,.若为实数,,则 。
10.设 的最大值为16,则 。
11.已知,,则 。
12.在△中,内角、、的对边分别为、、,已知,,,则 。
13.若关于的不等式存在实数解,则实数的取值范围是 。
14.函数.给出函数下列性质:①函数的定义域和值域均为;②函数的图像关于原点成中心对称;③函数在定义域上单调递增;④(其中为函数的定义域);⑤、为函数图象上任意不同两点,则。请写出所有关于函数性质正确描述的序号 。
三、解答题:(本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤.)
15.(本小题满分12分)
已知集合,.
(Ⅰ)求集合和集合;
(Ⅱ)若,求的取值范围。
16.(本小题满分12分)
在直角坐标系中,已知,,为坐标原点,,.
(Ⅰ)求的对称中心的坐标及其在区间上的单调递减区间;
(Ⅱ)若,,求的值。
17.(本小题满分14分)21世纪教育网
已知函数,
(Ⅰ)求函数的最大值和最小正周期;
(Ⅱ)设的内角的对边分别且,,若,求的值.
18.(本小题满分14分)
已知函数,
(Ⅰ)若,求的单调区间;
(Ⅱ)在(Ⅰ)的条件下,对,都有,求实数的取值范围;
(Ⅲ)若在,上单调递增,在上单调递减,求实数的取值范围。
19.(本小题满分14分)
如图:某污水处理厂要在一个矩形污水处理池的池底水平铺设污水净化管道,是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口是的中点,分别落在线段上。已知米,米,记。
(Ⅰ)试将污水净化管道的长度表示为的函数,并写出定义域;
(Ⅱ)若,求此时管道的长度;
(Ⅲ)问:当取何值时,铺设管道的成本最低?并求出此时管道的长度。
20.(本小题满分14分)
已知函数的单调递增区间为,
(Ⅰ)求证:;
(Ⅱ)当取最小值时,点是函数图象上的两点,若存在使得,求证:
汕头市金山中学2012-2013学年度第一学期期中考试
高三理科数学 答题卷
班级 姓名 学号 评分
一、选择题(40分)
题号
1
2
3
4
5
6
7
8
答案
二、填空题(30分)
9. 10. 11. 12. 13.
14. 。
三、解答题(80分)
15.(本小题满分12分)
16.(本小题满分12分)
17.(本小题满分14分)
姓名 学号
18.(本小题满分14分)
19.(本小题满分14分)
21世纪教育网
20.(本小题满分14分)
汕头市金山中学2012-2013学年度第一学期期中考试
高三理科数学 参考答案
一、选择题(40分)
题号
1
2
3
4
5
6
7
8
答案
D
A
C
A
D
B
C
C
二、填空题(30分)
9. 10. 11. 12. 13. 14.②④
三、解答题(80分)
15.解:(Ⅰ)由,得,即…………………3分
由或,
即………………………………………………………………………6分
(Ⅱ),
的取值范围是…………………………………………………………………12分
16.解:,,
则……………21世纪教育网……………………2分
……………………………………………………4分
(Ⅰ)由,即对称中心是
当时单调递减,即
的单调递减是………………………………………6分
在区间上的单调递减区间为.………………………………………8分
(Ⅱ)
……………………………………10分
。…………………………………………………12分
17.解:(Ⅰ)…………………………2分
则的最大值为0,最小正周期是……………………………………………4分
(Ⅱ)则
……………………………………………………………………………6分
由正弦定理得①…………21世纪教育网…………………9分
由余弦定理得
即②……………………………………………………………………………12分
由①②解得,…………………………………………………………………14分
18.解:(Ⅰ)定义域为
当时,,,令得或(舍)
(0,2)
2
-
0
+
↘
↗
∴的递减区间为(0,2),递增区间为…………………………………………4分
(Ⅱ)∵都有成立
∴………………………………………………………………………………5分
由(Ⅰ)知
,……………………………………………7分
∴,∴……………………………………………………………………8分
(Ⅲ)…………………………………9分
由条件知恰为的两个不相等正根,
即恰有两个不相等正根,……………………………………………10分
对于方程显然是方程的一个解,……………………………11分
当时,(且)
当时,
当时,…………………………………………………………………13分
∴且…………………………………………21世纪教育网……………………14分
19.解:(Ⅰ),,
由于,,,。……3分
所以 ,………………………………………………5分
(Ⅱ)时,,;…………………………10分
(Ⅲ)=,设,
则,由于,
所以 ,在 内单调递减,
于是当时. 的最小值米……………………………………………13分
答:当时,所铺设管道的成本最低,此时管道的长度为米………………14分
20.解:(Ⅰ)……………………………………………………………2分
依题意是方程的两根有:………………………………4分
……………6分
(Ⅱ)
取最小值时,,……………………………………………………7分
在上是增函数,,
,从而………………………………………………8分
即
…………………21世纪教育网…………10分
考虑函数,因,故当时,有,
所以是上是减函数.
由,得………21世纪教育网…………………………12分
由及得
故,即.
……………………………………………21世纪教育网……………………………14分
同课章节目录
