2021-2022学年北师大版九年级数学下册1.1第1课时正切同步练习(Word版,附答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册1.1第1课时正切同步练习(Word版,附答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 182.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-19 23:23:44 | ||
图片预览


文档简介
1.1 第1课时 正切
【基础练习】
知识点1 正切
1.如图1,在Rt△ABC中,若∠C=90°,BC=5,AC=12,AB=13,则tanA的值为 ( )
图1
A. B. C. D.
2.若Rt△ABC的各边都扩大为原来的4倍,则锐角A的正切值 ( )
A.扩大为原来的4倍 B.不变
C.缩小为原来的 D.以上都不对
3.如图2,在Rt△ABC中,∠C=90°,BC=12cm,AB=20cm,则tanA= ,tanB= .
图2
4.[教材习题1.1第2题变式题]如图3,在Rt△ABC中,∠C=90°,BC=15,tanA=,求AB的长.
图3
知识点2 正切与梯子的倾斜程度的关系
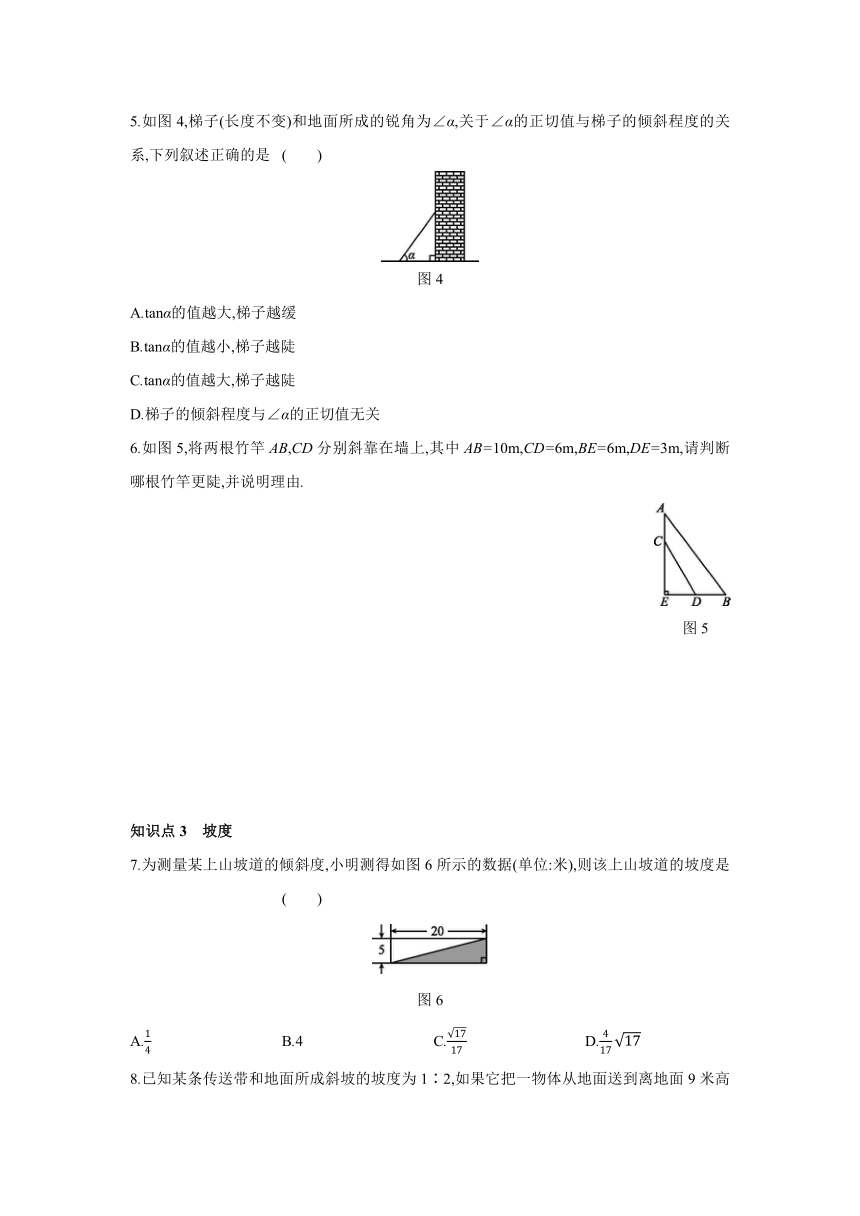
5.如图4,梯子(长度不变)和地面所成的锐角为∠α,关于∠α的正切值与梯子的倾斜程度的关系,下列叙述正确的是 ( )
图4
A.tanα的值越大,梯子越缓
B.tanα的值越小,梯子越陡
C.tanα的值越大,梯子越陡
D.梯子的倾斜程度与∠α的正切值无关
6.如图5,将两根竹竿AB,CD分别斜靠在墙上,其中AB=10m,CD=6m,BE=6m,DE=3m,请判断哪根竹竿更陡,并说明理由.
图5
知识点3 坡度
7.为测量某上山坡道的倾斜度,小明测得如图6所示的数据(单位:米),则该上山坡道的坡度是 ( )
图6
A. B.4 C. D.
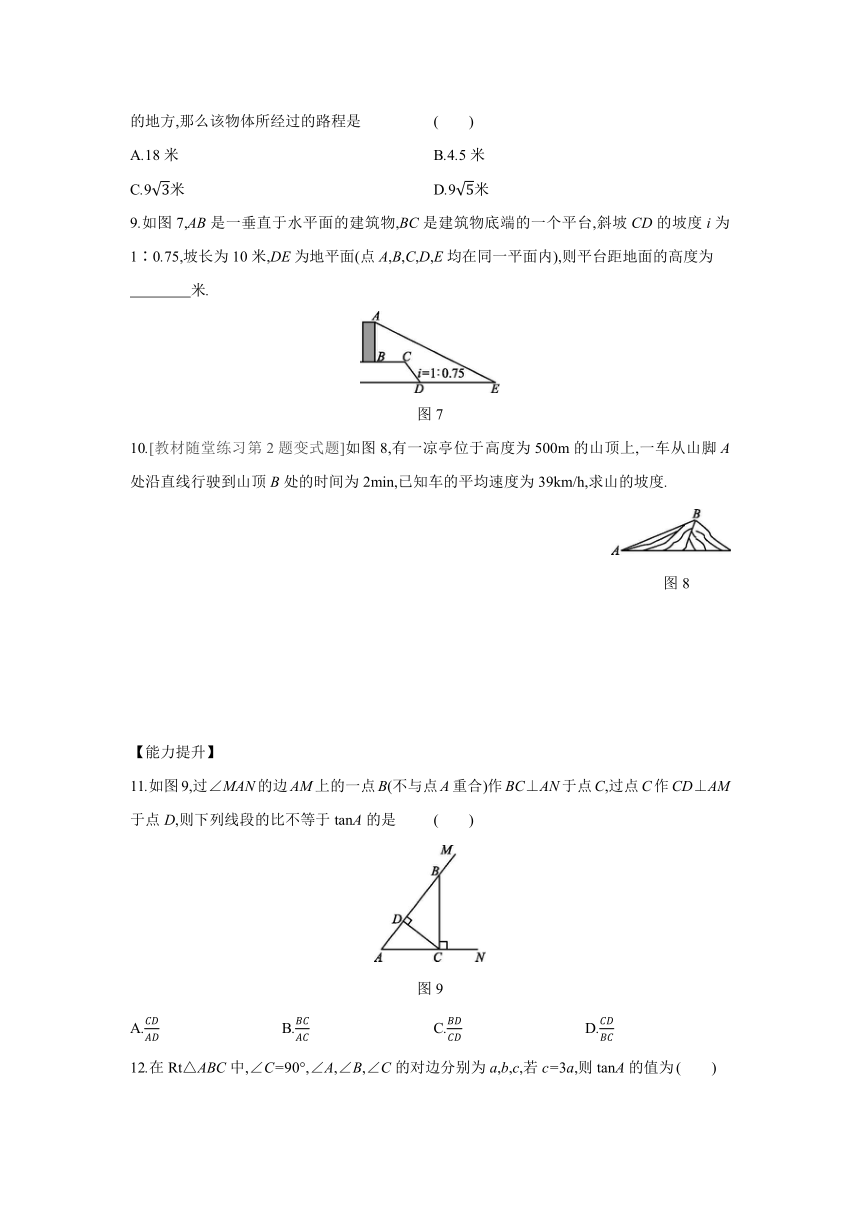
8.已知某条传送带和地面所成斜坡的坡度为1∶2,如果它把一物体从地面送到离地面9米高的地方,那么该物体所经过的路程是 ( )
A.18米 B.4.5米
C.9米 D.9米
9.如图7,AB是一垂直于水平面的建筑物,BC是建筑物底端的一个平台,斜坡CD的坡度i为1∶0.75,坡长为10米,DE为地平面(点A,B,C,D,E均在同一平面内),则平台距地面的高度为
米.
图7
10.[教材随堂练习第2题变式题]如图8,有一凉亭位于高度为500m的山顶上,一车从山脚A处沿直线行驶到山顶B处的时间为2min,已知车的平均速度为39km/h,求山的坡度.
图8
【能力提升】
11.如图9,过∠MAN的边AM上的一点B(不与点A重合)作BC⊥AN于点C,过点C作CD⊥AM于点D,则下列线段的比不等于tanA的是 ( )
图9
A. B. C. D.
12.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,若c=3a,则tanA的值为 ( )
A. B. C. D.3
13.如图10所示,△ABC的顶点在正方形网格的格点上,则tanA的值为( )
图10
A. B. C.2 D.2
14.在平面直角坐标系中,P是第一象限内的点,其坐标是(t,3),且OP与x轴正方向的夹角α的正切值是,则t的值是 .
15.如图11,在Rt△ABC中,∠ACB=90°,AB=3,tanB=,将△ABC绕着点A顺时针旋转90°后,点B落在点D处,点C落在点E处,射线DE与边AB相交于点F,那么BF= .
图11
16.如图12,在△ABC中,AB=AC=5,BC=8.若∠BPC=∠BAC,则tan∠BPC= .
图12
17.如图13,某公园入口处原有三级台阶,每级台阶高为18cm,宽为30cm.为方便残疾人士进出,打算将台阶改为斜坡.设台阶的起始点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1∶5,则AC的长是 cm.
图13
18.如图14,在锐角三角形ABC中,AB=10,BC=9,△ABC的面积为27,求tanC的值.
图14
19.如图15,将矩形ABCD沿对角线BD所在直线翻折后,点A与点E重合,且ED交BC于点F,连接AE,如果tan∠DFC=,那么的值是 .
图15
答案
1.A [解析]tanA==.故选A.
2.B [解析]设在原Rt△ABC中,锐角A的对边长与邻边长分别为a,b,各边都扩大为原来的4倍后,∠A的对边长与邻边长分别为4a,4b,此时tanA==.
3. [解析]在Rt△ABC中,∵∠C=90°,BC=12cm,AB=20cm,
∴AC===16(cm),
∴tanA==,tanB==.
4.解:∵∠C=90°,tanA=,
∴=.
又∵BC=15,∴AC=8.
在Rt△ABC中,由勾股定理,得AB===17.
5.C
6.解:竹竿CD更陡.理由如下:
在Rt△ABE中,
∵∠E=90°,AB=10m,BE=6m,
∴AE===8(m),
∴tanB===.
在Rt△CDE中,
∵∠E=90°,CD=6m,DE=3m,
∴CE===3(m),
∴tan∠CDE===.
∵<,∴竹竿CD更陡.
7.A [解析]如图,AB=20米,BC=5米,∠A=α,∠B=90°,∴tanα===.故选A.
8.D
9.8
10.解:过点B作BC⊥AC,如图.在Rt△ABC中,AB=39×=1.3(km),BC=500m=0.5km,
∴AC===1.2(km),
∴山的坡度为tanA===,
∴山的坡度为.
11.D 12.B
13.A [解析]如图,连接BD,由网格的特点可得BD⊥AC.
设小正方形的边长均为1,
则AD==2,BD==,
∴tanA===.
故选A.
14.4
15. [解析]△ABC绕着点A顺时针旋转90°得到△ADE,
则△ABC≌△ADE,∠BAD=90°,且∠B=∠D,AB=AD=3.
在Rt△DAF中,tanD=tanB==,
则AF=,则BF=.
16. 17.210
18.解:如图,过点A作AH⊥BC于点H.
∵S△ABC=27,
∴BC·AH=27.
∵BC=9,∴AH=6.
在Rt△ABH中,∵AB=10,
∴BH===8,
∴HC=BC-BH=9-8=1,
∴在Rt△AHC中,tanC===6.
19. [解析]∵四边形ABCD是矩形,
∴BC=AD,AB=CD,∠DAB=∠C=90°,AD∥BC,
∴∠ADB=∠DBC.
∵矩形ABCD沿对角线BD所在直线翻折后,点A与点E重合,
∴DE=AD,AB=BE,∠BED=∠DAB=90°,∠ADB=∠BDE,
∴∠DBF=∠FDB,DE=BC,BE=CD,
∴BF=DF,∴EF=CF.
∵tan∠DFC=tan∠BFE=,
∴设CD=BE=3x,CF=EF=4x,则DF=BF=5x,BC=9x.
在Rt△BCD中,BD====3x.
翻折后,点A与点E重合,则AE⊥BD,BD平分AE,
则AE=2=2×=x,
则=3x÷x=.
【基础练习】
知识点1 正切
1.如图1,在Rt△ABC中,若∠C=90°,BC=5,AC=12,AB=13,则tanA的值为 ( )
图1
A. B. C. D.
2.若Rt△ABC的各边都扩大为原来的4倍,则锐角A的正切值 ( )
A.扩大为原来的4倍 B.不变
C.缩小为原来的 D.以上都不对
3.如图2,在Rt△ABC中,∠C=90°,BC=12cm,AB=20cm,则tanA= ,tanB= .
图2
4.[教材习题1.1第2题变式题]如图3,在Rt△ABC中,∠C=90°,BC=15,tanA=,求AB的长.
图3
知识点2 正切与梯子的倾斜程度的关系
5.如图4,梯子(长度不变)和地面所成的锐角为∠α,关于∠α的正切值与梯子的倾斜程度的关系,下列叙述正确的是 ( )
图4
A.tanα的值越大,梯子越缓
B.tanα的值越小,梯子越陡
C.tanα的值越大,梯子越陡
D.梯子的倾斜程度与∠α的正切值无关
6.如图5,将两根竹竿AB,CD分别斜靠在墙上,其中AB=10m,CD=6m,BE=6m,DE=3m,请判断哪根竹竿更陡,并说明理由.
图5
知识点3 坡度
7.为测量某上山坡道的倾斜度,小明测得如图6所示的数据(单位:米),则该上山坡道的坡度是 ( )
图6
A. B.4 C. D.
8.已知某条传送带和地面所成斜坡的坡度为1∶2,如果它把一物体从地面送到离地面9米高的地方,那么该物体所经过的路程是 ( )
A.18米 B.4.5米
C.9米 D.9米
9.如图7,AB是一垂直于水平面的建筑物,BC是建筑物底端的一个平台,斜坡CD的坡度i为1∶0.75,坡长为10米,DE为地平面(点A,B,C,D,E均在同一平面内),则平台距地面的高度为
米.
图7
10.[教材随堂练习第2题变式题]如图8,有一凉亭位于高度为500m的山顶上,一车从山脚A处沿直线行驶到山顶B处的时间为2min,已知车的平均速度为39km/h,求山的坡度.
图8
【能力提升】
11.如图9,过∠MAN的边AM上的一点B(不与点A重合)作BC⊥AN于点C,过点C作CD⊥AM于点D,则下列线段的比不等于tanA的是 ( )
图9
A. B. C. D.
12.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,若c=3a,则tanA的值为 ( )
A. B. C. D.3
13.如图10所示,△ABC的顶点在正方形网格的格点上,则tanA的值为( )
图10
A. B. C.2 D.2
14.在平面直角坐标系中,P是第一象限内的点,其坐标是(t,3),且OP与x轴正方向的夹角α的正切值是,则t的值是 .
15.如图11,在Rt△ABC中,∠ACB=90°,AB=3,tanB=,将△ABC绕着点A顺时针旋转90°后,点B落在点D处,点C落在点E处,射线DE与边AB相交于点F,那么BF= .
图11
16.如图12,在△ABC中,AB=AC=5,BC=8.若∠BPC=∠BAC,则tan∠BPC= .
图12
17.如图13,某公园入口处原有三级台阶,每级台阶高为18cm,宽为30cm.为方便残疾人士进出,打算将台阶改为斜坡.设台阶的起始点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1∶5,则AC的长是 cm.
图13
18.如图14,在锐角三角形ABC中,AB=10,BC=9,△ABC的面积为27,求tanC的值.
图14
19.如图15,将矩形ABCD沿对角线BD所在直线翻折后,点A与点E重合,且ED交BC于点F,连接AE,如果tan∠DFC=,那么的值是 .
图15
答案
1.A [解析]tanA==.故选A.
2.B [解析]设在原Rt△ABC中,锐角A的对边长与邻边长分别为a,b,各边都扩大为原来的4倍后,∠A的对边长与邻边长分别为4a,4b,此时tanA==.
3. [解析]在Rt△ABC中,∵∠C=90°,BC=12cm,AB=20cm,
∴AC===16(cm),
∴tanA==,tanB==.
4.解:∵∠C=90°,tanA=,
∴=.
又∵BC=15,∴AC=8.
在Rt△ABC中,由勾股定理,得AB===17.
5.C
6.解:竹竿CD更陡.理由如下:
在Rt△ABE中,
∵∠E=90°,AB=10m,BE=6m,
∴AE===8(m),
∴tanB===.
在Rt△CDE中,
∵∠E=90°,CD=6m,DE=3m,
∴CE===3(m),
∴tan∠CDE===.
∵<,∴竹竿CD更陡.
7.A [解析]如图,AB=20米,BC=5米,∠A=α,∠B=90°,∴tanα===.故选A.
8.D
9.8
10.解:过点B作BC⊥AC,如图.在Rt△ABC中,AB=39×=1.3(km),BC=500m=0.5km,
∴AC===1.2(km),
∴山的坡度为tanA===,
∴山的坡度为.
11.D 12.B
13.A [解析]如图,连接BD,由网格的特点可得BD⊥AC.
设小正方形的边长均为1,
则AD==2,BD==,
∴tanA===.
故选A.
14.4
15. [解析]△ABC绕着点A顺时针旋转90°得到△ADE,
则△ABC≌△ADE,∠BAD=90°,且∠B=∠D,AB=AD=3.
在Rt△DAF中,tanD=tanB==,
则AF=,则BF=.
16. 17.210
18.解:如图,过点A作AH⊥BC于点H.
∵S△ABC=27,
∴BC·AH=27.
∵BC=9,∴AH=6.
在Rt△ABH中,∵AB=10,
∴BH===8,
∴HC=BC-BH=9-8=1,
∴在Rt△AHC中,tanC===6.
19. [解析]∵四边形ABCD是矩形,
∴BC=AD,AB=CD,∠DAB=∠C=90°,AD∥BC,
∴∠ADB=∠DBC.
∵矩形ABCD沿对角线BD所在直线翻折后,点A与点E重合,
∴DE=AD,AB=BE,∠BED=∠DAB=90°,∠ADB=∠BDE,
∴∠DBF=∠FDB,DE=BC,BE=CD,
∴BF=DF,∴EF=CF.
∵tan∠DFC=tan∠BFE=,
∴设CD=BE=3x,CF=EF=4x,则DF=BF=5x,BC=9x.
在Rt△BCD中,BD====3x.
翻折后,点A与点E重合,则AE⊥BD,BD平分AE,
则AE=2=2×=x,
则=3x÷x=.
