2021-2022学年北师大版九年级数学下册1.5三角函数的应用同步练习(Word版,附答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册1.5三角函数的应用同步练习(Word版,附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 171.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-19 23:34:40 | ||
图片预览


文档简介
5 三角函数的应用
【基础练习】
知识点1 解决与方向角有关的问题
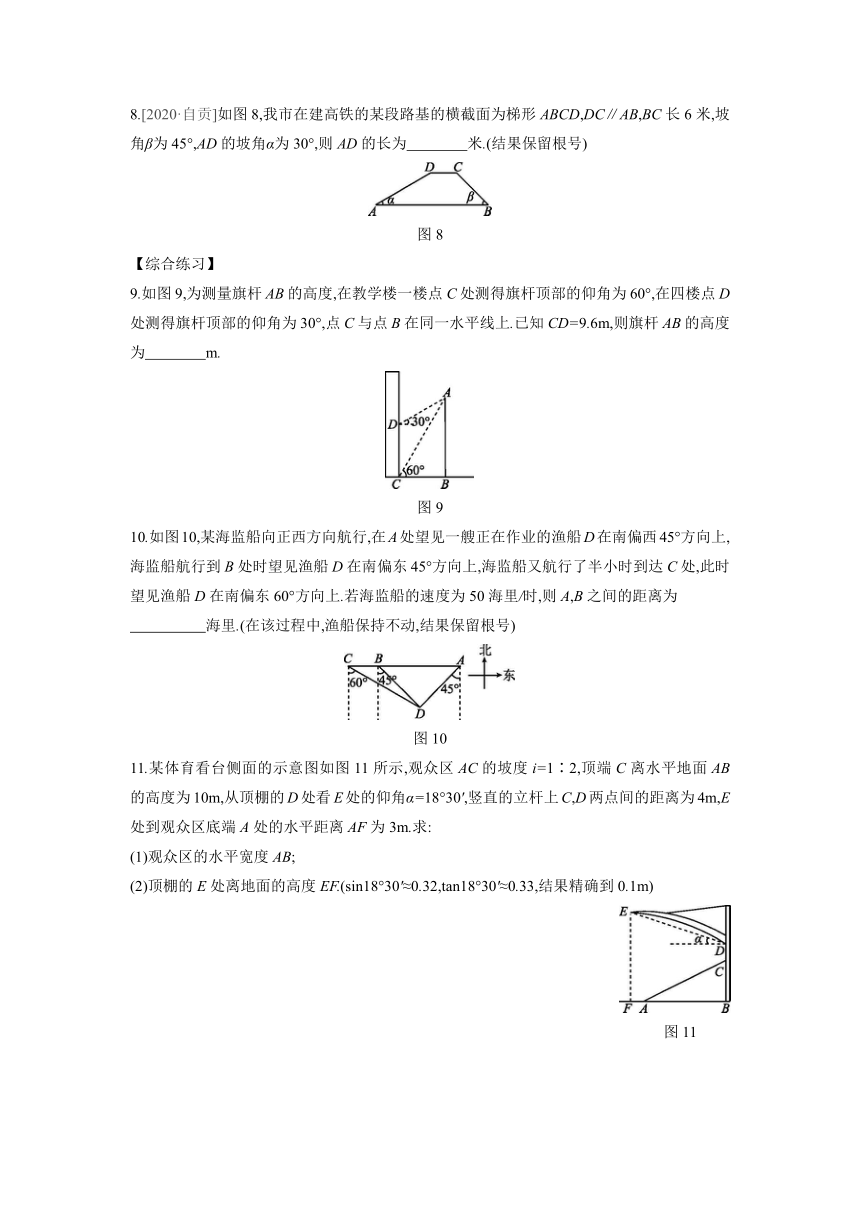
1.如图1,小雅家(图中点O处)门前有一条东西走向的公路,一水塔(图中点A处)在她家北偏东60°方向上,且距离她家500米处,那么水塔所在的位置到公路的距离AB的长为 ( )
图1
A.250米 B.250米
C.米 D.500米
2.[2021·武汉]如图2,海中有一个小岛A.一艘轮船由西向东航行,在点B测得小岛A在北偏东60°方向上,航行12nmile到达点C,这时测得小岛A在北偏东30°方向上.小岛A到航线BC的距离是 nmile(参考数据:≈1.73,结果精确到0.1nmile)
图2
3.如图3,一艘轮船以每小时30海里的速度自东向西航行,在A处测得小岛P位于其西北方向(北偏西45°方向),2小时后轮船到达B处,在B处测得小岛P位于其北偏东60°方向.求此时船与小岛P的距离.(结果保留整数,参考数据:≈1.414,≈1.732)
图3
知识点2 解决与仰角、俯角有关的问题
4.如图4,某地修建高速公路,要从A地向B地修一条隧道(点A,B在同一水平面上).为了测量A,B两地之间的距离,一架直升机从A地出发,垂直上升800m到达C处,在C处观察B地的俯角为α,则A,B两地之间的距离为 ( )
图4
A.800sinαm B.800tanαm
C.m D.m
5如图5,建筑物BC上有一根旗杆AB.从与BC相距10m的D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则旗杆AB的高度约为
m.(结果取整数,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
图5
6.如图6,两座建筑物的水平距离BC=30m,从点A测得点D的俯角α为30°,测得点C的俯角β为60°,求这两座建筑物的高度.(结果保留根号)
图6
知识点3 解决与坡度、坡角有关的问题
7.如图7,某水库堤坝横断面迎水坡AB的坡度是3∶4,迎水坡AB的长度是50m,则堤坝高BC为 ( )
图7
A.30m B.40m C.50m D.60m
8.[2020·自贡]如图8,我市在建高铁的某段路基的横截面为梯形ABCD,DC∥AB,BC长6米,坡角β为45°,AD的坡角α为30°,则AD的长为 米.(结果保留根号)
图8
【综合练习】
9.如图9,为测量旗杆AB的高度,在教学楼一楼点C处测得旗杆顶部的仰角为60°,在四楼点D处测得旗杆顶部的仰角为30°,点C与点B在同一水平线上.已知CD=9.6m,则旗杆AB的高度为 m.
图9
10.如图10,某海监船向正西方向航行,在A处望见一艘正在作业的渔船D在南偏西45°方向上,海监船航行到B处时望见渔船D在南偏东45°方向上,海监船又航行了半小时到达C处,此时望见渔船D在南偏东60°方向上.若海监船的速度为50海里/时,则A,B之间的距离为
海里.(在该过程中,渔船保持不动,结果保留根号)
图10
11.某体育看台侧面的示意图如图11所示,观众区AC的坡度i=1∶2,顶端C离水平地面AB的高度为10m,从顶棚的D处看E处的仰角α=18°30',竖直的立杆上C,D两点间的距离为4m,E处到观众区底端A处的水平距离AF为3m.求:
(1)观众区的水平宽度AB;
(2)顶棚的E处离地面的高度EF.(sin18°30'≈0.32,tan18°30'≈0.33,结果精确到0.1m)
图11
12.如图12,某旅游景区为方便游客,修建了一条东西走向的木栈道AB,木栈道AB与景区道路CD平行.在C处测得木栈道一端A位于北偏西42°方向,在D处测得木栈道另一端B位于北偏西32°方向.已知CD=120m,BD=80m,求木栈道AB的长度.结果保留整数,参考数据:sin32°≈,cos32°≈,tan32°≈,sin42°≈,cos42°≈,tan42°≈
图12
答案
1.A
2.10.4 [解析]过点A作AE⊥BC交BC的延长线于点E,如图.
由题意,易得∠ACE=60°,∠ABC=30°,
∴∠BAC=∠ACE-∠ABC=30°,
∴∠BAC=∠ABC,
∴AC=BC=12nmile.
在Rt△ACE中,sin∠ACE=,
∴AE=AC·sin∠ACE=6≈10.4(nmile).
故小岛A到航线BC的距离约是10.4nmile.
3.解:如图,过点P作PH⊥AB于点H.
由题意,得AB=30×2=60(海里),∠PBH=90°-60°=30°,∠PAH=90°-45°=45°,
则△PHA是等腰直角三角形,
∴AH=PH.
在Rt△PHA中,设AH=PH=x海里,
在Rt△PBH中,PB=2PH=2x海里,BH=AB-AH=(60-x)海里,
∴tan∠PBH=tan30°==,
∴=,
解得x=30(-1),
∴PB=2x=60(-1)≈44(海里).
故此时船与小岛P的距离约为44海里.
4.D
5.3
6.解:如图,延长CD交AE于点E,可得DE⊥AE.
在Rt△AED中,AE=BC=30m,∠EAD=30°,
∴ED=AE·tan30°=10m.
在Rt△ABC中,∠ACB=60°,BC=30m,
∴AB=BC·tan60°=30m,
∴CD=EC-ED=AB-ED=30-10=20(m).
因此,建筑物AB的高度为30m,建筑物CD的高度为20m.
7.A
8.6 [解析]如图,过点D作DE⊥AB于点E,过点C作CF⊥AB于点F.
∵CD∥AB,DE⊥AB,CF⊥AB,
∴DE=CF.
在Rt△CFB中,CF=BC·sinβ=6sin45°=3(米),
∴DE=CF=3米.
在Rt△ADE中,∵∠A=30°,∠AED=90°,
∴AD=2DE=6米.
故答案为6.
9.14.4
10.25(+1) [解析]∵∠DBA=∠DAB=45°,
∴△DAB是等腰直角三角形.
过点D作DE⊥AB于点E,则DE=AB=BE=AE.设DE=x,则AB=2x.
在Rt△CDE中,∠DCE=30°,
则CE=DE=x.
由题意,得CB=CE-BE=x-x=25,
解得x==.
∴AB=2×=25(+1)海里.
故答案为25(+1).
11.解:(1)∵观众区AC的坡度i=1∶2,顶端C离水平地面AB的高度为10m,即BC=10m,
∴AB=2BC=20m.
即观众区的水平宽度AB为20m.
(2)如图,过点C作CM⊥EF于点M,过点D作DN⊥EF于点N,
则四边形MFBC,MCDN均为矩形,
∴MF=BC=10m,MN=CD=4m,DN=MC=BF=AB+AF=20+3=23(m).
在Rt△END中,tan∠EDN=,
∴EN=DN·tan∠EDN≈23×0.33=7.59(m),
∴EF=EN+MN+MF≈7.59+4+10≈21.6(m).
故顶棚的E处离地面的高度EF约为21.6m.
12.解:如图,过点C作CE⊥AB于点E,过点D作DF⊥AB交AB的延长线于点F,则CE∥DF.
又∵AB∥CD,CE⊥AB,
∴四边形CDFE是矩形,
∴EF=CD=120m,DF=CE.
在Rt△BDF中,∵∠BDF=32°,BD=80m,
∴DF=BD·cos32°≈80×=68(m),BF=BD·sin32°≈80×=(m),
∴BE=EF-BF≈120-=(m).
在Rt△ACE中,∵∠ACE=42°,CE=DF≈68m,
∴AE=CE·tan42°≈68×=(m),
∴AB=BE+AE≈+≈139(m).
故木栈道AB的长度约为139m.
【基础练习】
知识点1 解决与方向角有关的问题
1.如图1,小雅家(图中点O处)门前有一条东西走向的公路,一水塔(图中点A处)在她家北偏东60°方向上,且距离她家500米处,那么水塔所在的位置到公路的距离AB的长为 ( )
图1
A.250米 B.250米
C.米 D.500米
2.[2021·武汉]如图2,海中有一个小岛A.一艘轮船由西向东航行,在点B测得小岛A在北偏东60°方向上,航行12nmile到达点C,这时测得小岛A在北偏东30°方向上.小岛A到航线BC的距离是 nmile(参考数据:≈1.73,结果精确到0.1nmile)
图2
3.如图3,一艘轮船以每小时30海里的速度自东向西航行,在A处测得小岛P位于其西北方向(北偏西45°方向),2小时后轮船到达B处,在B处测得小岛P位于其北偏东60°方向.求此时船与小岛P的距离.(结果保留整数,参考数据:≈1.414,≈1.732)
图3
知识点2 解决与仰角、俯角有关的问题
4.如图4,某地修建高速公路,要从A地向B地修一条隧道(点A,B在同一水平面上).为了测量A,B两地之间的距离,一架直升机从A地出发,垂直上升800m到达C处,在C处观察B地的俯角为α,则A,B两地之间的距离为 ( )
图4
A.800sinαm B.800tanαm
C.m D.m
5如图5,建筑物BC上有一根旗杆AB.从与BC相距10m的D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则旗杆AB的高度约为
m.(结果取整数,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
图5
6.如图6,两座建筑物的水平距离BC=30m,从点A测得点D的俯角α为30°,测得点C的俯角β为60°,求这两座建筑物的高度.(结果保留根号)
图6
知识点3 解决与坡度、坡角有关的问题
7.如图7,某水库堤坝横断面迎水坡AB的坡度是3∶4,迎水坡AB的长度是50m,则堤坝高BC为 ( )
图7
A.30m B.40m C.50m D.60m
8.[2020·自贡]如图8,我市在建高铁的某段路基的横截面为梯形ABCD,DC∥AB,BC长6米,坡角β为45°,AD的坡角α为30°,则AD的长为 米.(结果保留根号)
图8
【综合练习】
9.如图9,为测量旗杆AB的高度,在教学楼一楼点C处测得旗杆顶部的仰角为60°,在四楼点D处测得旗杆顶部的仰角为30°,点C与点B在同一水平线上.已知CD=9.6m,则旗杆AB的高度为 m.
图9
10.如图10,某海监船向正西方向航行,在A处望见一艘正在作业的渔船D在南偏西45°方向上,海监船航行到B处时望见渔船D在南偏东45°方向上,海监船又航行了半小时到达C处,此时望见渔船D在南偏东60°方向上.若海监船的速度为50海里/时,则A,B之间的距离为
海里.(在该过程中,渔船保持不动,结果保留根号)
图10
11.某体育看台侧面的示意图如图11所示,观众区AC的坡度i=1∶2,顶端C离水平地面AB的高度为10m,从顶棚的D处看E处的仰角α=18°30',竖直的立杆上C,D两点间的距离为4m,E处到观众区底端A处的水平距离AF为3m.求:
(1)观众区的水平宽度AB;
(2)顶棚的E处离地面的高度EF.(sin18°30'≈0.32,tan18°30'≈0.33,结果精确到0.1m)
图11
12.如图12,某旅游景区为方便游客,修建了一条东西走向的木栈道AB,木栈道AB与景区道路CD平行.在C处测得木栈道一端A位于北偏西42°方向,在D处测得木栈道另一端B位于北偏西32°方向.已知CD=120m,BD=80m,求木栈道AB的长度.结果保留整数,参考数据:sin32°≈,cos32°≈,tan32°≈,sin42°≈,cos42°≈,tan42°≈
图12
答案
1.A
2.10.4 [解析]过点A作AE⊥BC交BC的延长线于点E,如图.
由题意,易得∠ACE=60°,∠ABC=30°,
∴∠BAC=∠ACE-∠ABC=30°,
∴∠BAC=∠ABC,
∴AC=BC=12nmile.
在Rt△ACE中,sin∠ACE=,
∴AE=AC·sin∠ACE=6≈10.4(nmile).
故小岛A到航线BC的距离约是10.4nmile.
3.解:如图,过点P作PH⊥AB于点H.
由题意,得AB=30×2=60(海里),∠PBH=90°-60°=30°,∠PAH=90°-45°=45°,
则△PHA是等腰直角三角形,
∴AH=PH.
在Rt△PHA中,设AH=PH=x海里,
在Rt△PBH中,PB=2PH=2x海里,BH=AB-AH=(60-x)海里,
∴tan∠PBH=tan30°==,
∴=,
解得x=30(-1),
∴PB=2x=60(-1)≈44(海里).
故此时船与小岛P的距离约为44海里.
4.D
5.3
6.解:如图,延长CD交AE于点E,可得DE⊥AE.
在Rt△AED中,AE=BC=30m,∠EAD=30°,
∴ED=AE·tan30°=10m.
在Rt△ABC中,∠ACB=60°,BC=30m,
∴AB=BC·tan60°=30m,
∴CD=EC-ED=AB-ED=30-10=20(m).
因此,建筑物AB的高度为30m,建筑物CD的高度为20m.
7.A
8.6 [解析]如图,过点D作DE⊥AB于点E,过点C作CF⊥AB于点F.
∵CD∥AB,DE⊥AB,CF⊥AB,
∴DE=CF.
在Rt△CFB中,CF=BC·sinβ=6sin45°=3(米),
∴DE=CF=3米.
在Rt△ADE中,∵∠A=30°,∠AED=90°,
∴AD=2DE=6米.
故答案为6.
9.14.4
10.25(+1) [解析]∵∠DBA=∠DAB=45°,
∴△DAB是等腰直角三角形.
过点D作DE⊥AB于点E,则DE=AB=BE=AE.设DE=x,则AB=2x.
在Rt△CDE中,∠DCE=30°,
则CE=DE=x.
由题意,得CB=CE-BE=x-x=25,
解得x==.
∴AB=2×=25(+1)海里.
故答案为25(+1).
11.解:(1)∵观众区AC的坡度i=1∶2,顶端C离水平地面AB的高度为10m,即BC=10m,
∴AB=2BC=20m.
即观众区的水平宽度AB为20m.
(2)如图,过点C作CM⊥EF于点M,过点D作DN⊥EF于点N,
则四边形MFBC,MCDN均为矩形,
∴MF=BC=10m,MN=CD=4m,DN=MC=BF=AB+AF=20+3=23(m).
在Rt△END中,tan∠EDN=,
∴EN=DN·tan∠EDN≈23×0.33=7.59(m),
∴EF=EN+MN+MF≈7.59+4+10≈21.6(m).
故顶棚的E处离地面的高度EF约为21.6m.
12.解:如图,过点C作CE⊥AB于点E,过点D作DF⊥AB交AB的延长线于点F,则CE∥DF.
又∵AB∥CD,CE⊥AB,
∴四边形CDFE是矩形,
∴EF=CD=120m,DF=CE.
在Rt△BDF中,∵∠BDF=32°,BD=80m,
∴DF=BD·cos32°≈80×=68(m),BF=BD·sin32°≈80×=(m),
∴BE=EF-BF≈120-=(m).
在Rt△ACE中,∵∠ACE=42°,CE=DF≈68m,
∴AE=CE·tan42°≈68×=(m),
∴AB=BE+AE≈+≈139(m).
故木栈道AB的长度约为139m.
