人教版初中数学九年级上册 24.2.2直线与圆的位置关系课件(共18张PPT)
文档属性
| 名称 | 人教版初中数学九年级上册 24.2.2直线与圆的位置关系课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 272.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-18 14:31:03 | ||
图片预览

文档简介
(共18张PPT)
24.2.2直线和圆的位置关系
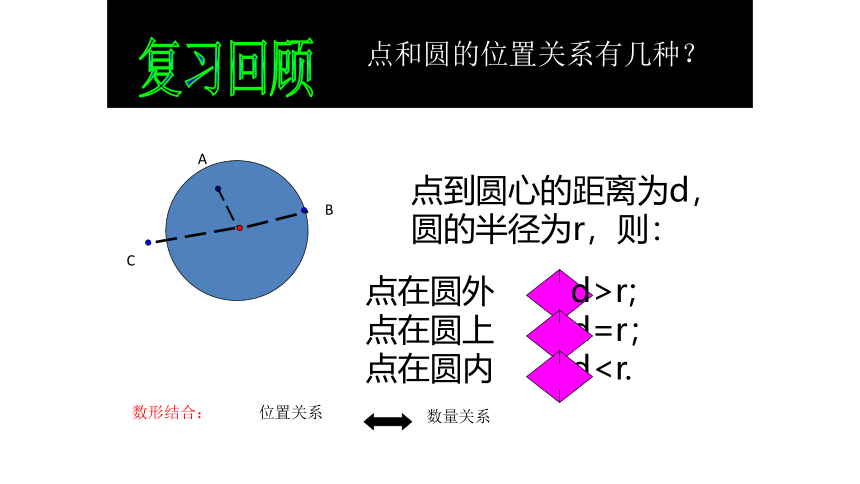
点和圆的位置关系有几种?
点到圆心的距离为d,圆的半径为r,则:
复习回顾
点在圆外 d>r;
点在圆上 d=r;
点在圆内 dA
B
C
位置关系
数形结合:
数量关系
a
.A
D
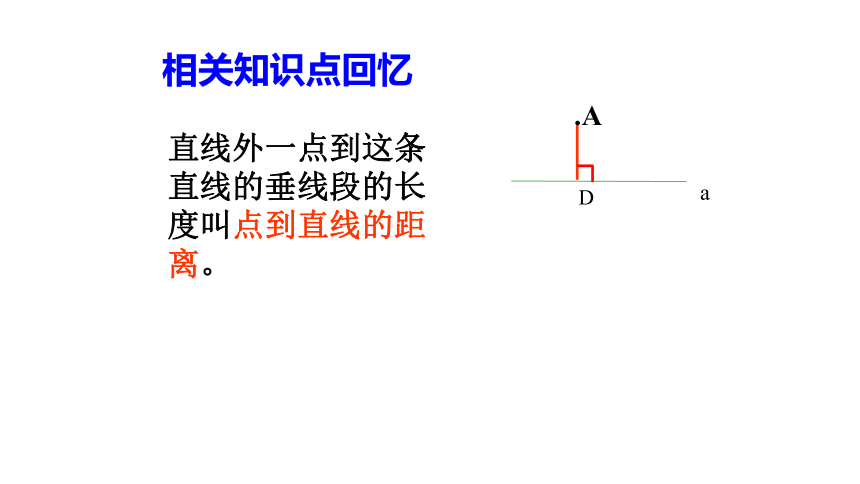
相关知识点回忆
直线外一点到这条直线的垂线段的长度叫点到直线的距离。
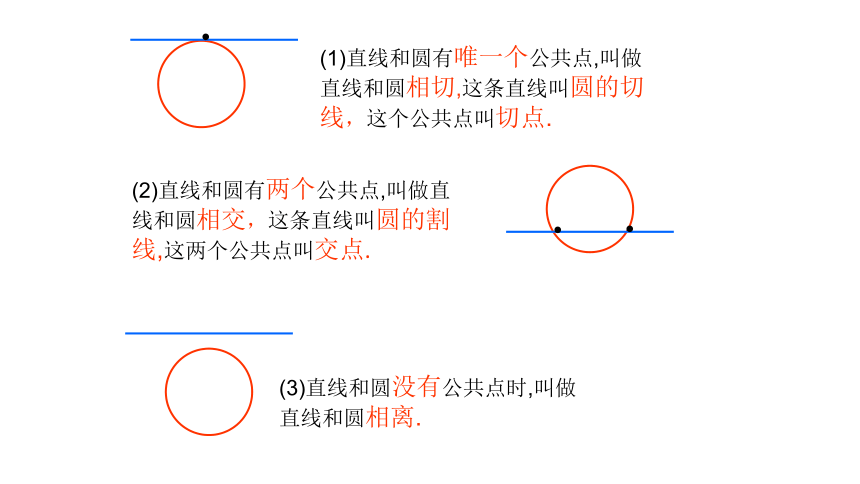
(1)直线和圆有唯一个公共点,叫做 直线和圆相切,这条直线叫圆的切线,这个公共点叫切点.
(2)直线和圆有两个公共点,叫做直 线和圆相交,这条直线叫圆的割线,这两个公共点叫交点.
(3)直线和圆没有公共点时,叫做
直线和圆相离.
·
·
·
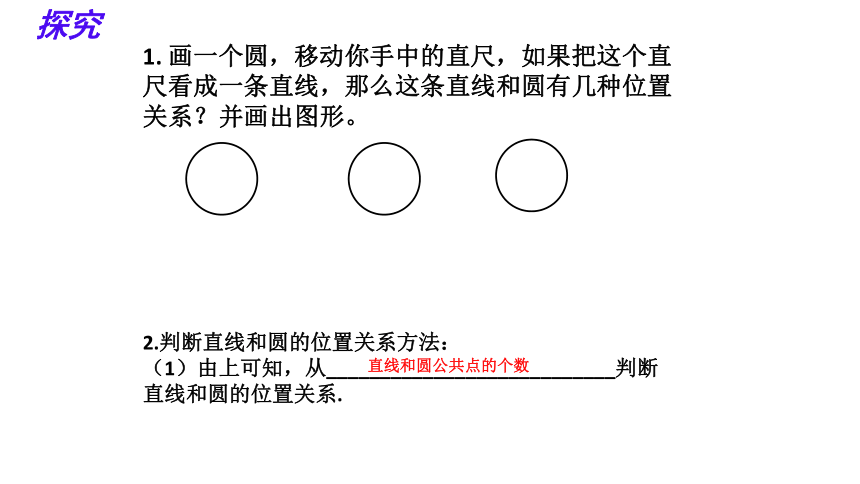
1. 画一个圆,移动你手中的直尺,如果把这个直尺看成一条直线,那么这条直线和圆有几种位置关系?并画出图形。
2.判断直线和圆的位置关系方法:
(1)由上可知,从___________________________判断直线和圆的位置关系.
直线和圆公共点的个数
探究
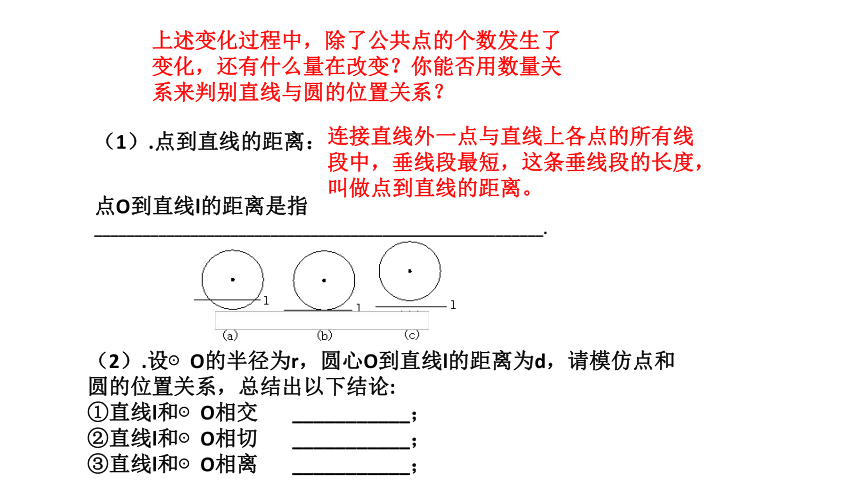
上述变化过程中,除了公共点的个数发生了变化,还有什么量在改变?你能否用数量关系来判别直线与圆的位置关系?
(1).点到直线的距离:
点O到直线l的距离是指________________________________________________________.
(2).设⊙O的半径为r,圆心O到直线l的距离为d,请模仿点和圆的位置关系,总结出以下结论:
①直线l和⊙O相交 ___________;
②直线l和⊙O相切 ___________;
③直线l和⊙O相离 ___________;
连接直线外一点与直线上各点的所有线段中,垂线段最短,这条垂线段的长度,叫做点到直线的距离。
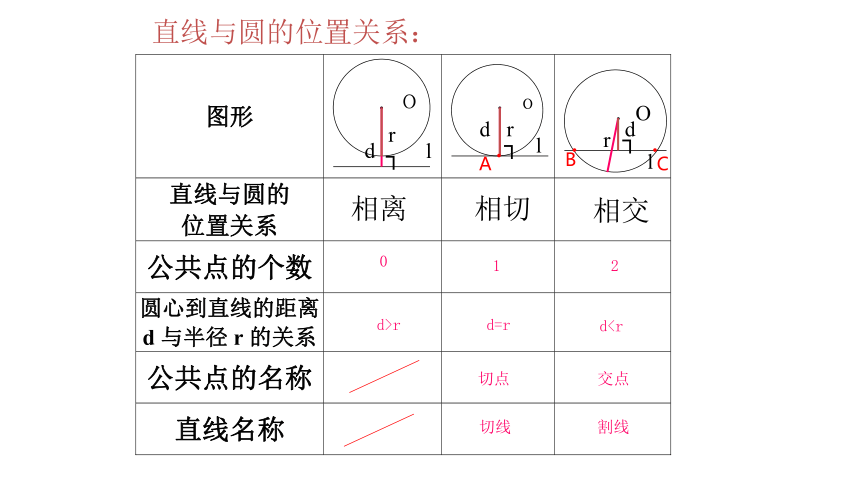
直线与圆的位置关系:
0
d>r
1
d=r
切点
切线
2
d交点
割线
.O
l
d
r
┐
┐
.o
l
d
r
.O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由 _______________ 的个数来判断;
(2)由_________________
的大小关系来判断。
两
直线与圆的公共点
圆心到直线的距离d与半径r
归纳:
如图:已知∠ AOB=30°,M为OB上一点,且OM=5cm,以M为圆心,以r为半径的圆与直线OA有怎样的位置关系?为什么?
(1)r=2cm; (2)r=4cm; (3)r=2.5cm.
解:过点M作MN⊥OA于点N
∵在Rt△OMN中,∠AOB=30°,OM=5cm. ∴MN=2.5CM
即圆心M到直线OA的距离d=2.5cm
(1)当r=2cm时, ∵d> r,
∴⊙M与直线OA相离。
(2)当r=4cm时, ∵d< r,
∴⊙M与直线OA相交。
(3)当r=2.5cm时, ∵d = r,
∴⊙M与直线OA相切。
做一做
2.5cm
开动脑筋
练一练
1.已知圆的直径为14cm,圆心到直线的距离为d,当d =9 cm时,直线和圆 ;当d =7 cm时,直线和圆 ;当d <6 cm时,直线和圆
2.已知⊙O的半径为5 cm,直线l上有一点B到圆心O的距离等于5 cm,则直线l和⊙O的位置关系是( ) .
A.相离 B.相切 C.相交 D.不能确定
相离
相切
相交
已知Rt△ABC的斜边AB=10cm,AC=6cm.画图说明
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切
(2)以点C为圆心,分别以4cm和5 cm的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系
思考:判断直线与圆位置关系的方法有哪些?
归纳: 根据(1)定义;(2)d与r的大小关系。
思考?
知识链接:
1.点O与直线m的距离为d,⊙O 的半径为r,若d,r是方程
的两个根,则直线m与⊙O的位置关系是 ______ 。
2.若d,r是方程 的两个根,且直线m与⊙O的位置关系是相切,则a的值是 。
3.如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,开始时,PO=6cm.如果⊙P以1cm/秒的速度沿由A向B的方向移动,那么当⊙P的运动时间t(秒)满足条件()时,⊙P与直线CD相交.
当堂检测
1、设⊙O的半径为4,点O到直线a的距离为d,
若⊙O与直线a至多只有一个公共点,则d为…( )
A、d≤4 B、d<4 C、d≥4 D、d=4
2、设⊙p的半径为4cm,直线l上一点A到圆心的
距离为4cm,则直线l与⊙O的位置关系
是……………………………………………( )
A、相交 B、相切 C、相离 D、相切或相交
C
D
当堂检测
3.⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l与⊙O没有公共点,则d为( )
A.d >3 B.d<3 C.d ≤3 D.d =3
4.圆心O到直线的距离等于⊙O的半径,则直线和⊙O的位置关系是( )
A.相离 B.相交 C.相切 D.相切或相交
A
C
5.已知⊙O的直径是10㎝,点O到直线L距离为d,若 直线L与⊙O相切,则d= ( )
A.d=10 B.d=5 C.d>5 D.d<5
B
6.直线L 和⊙O有公共点,则直线L与⊙O ( )
A.相离 B.相切 C.相交 D.相切或相交
D
7.判断:若直线和圆相切,则该直线和圆一定有一个公共点.( )
√
8.等边三角形ABC的边长为2,则以A为圆心,半径为1.7的圆与直线BC的位置关系是 ,以A为圆心,以 为半径的圆与直线BC相切.
相离
当堂检测
在Rt△ABC中,∠C=90°,
AC=3cm,BC=4cm,
以C为圆心,r为半径作圆。
想一想
当r满足___________
_______________ 时,⊙C与线段AB只有一个公共点.
r=2.4cm
B
C
A
D
4
5
3
d=2.4cm
或3cm2、识别直线与圆的位置关系的方法:
(1)一种是根据定义进行识别:
直线L与⊙o没有公共点 直线L与⊙o相离。
直线L与⊙o只有一个公共点 直线L与⊙o相切。
直线L与⊙o有两个公共点 直线L与⊙o相交。
(2)另一种是根据圆心到直线的距离d与圆半径r数量
比较来进行识别:
d>r 直线L与⊙o相离;
d=r 直线L与⊙o相切;
d1、直线与圆的位置关系3种:相离、相切和相交。
课堂小结
24.2.2直线和圆的位置关系
点和圆的位置关系有几种?
点到圆心的距离为d,圆的半径为r,则:
复习回顾
点在圆外 d>r;
点在圆上 d=r;
点在圆内 d
B
C
位置关系
数形结合:
数量关系
a
.A
D
相关知识点回忆
直线外一点到这条直线的垂线段的长度叫点到直线的距离。
(1)直线和圆有唯一个公共点,叫做 直线和圆相切,这条直线叫圆的切线,这个公共点叫切点.
(2)直线和圆有两个公共点,叫做直 线和圆相交,这条直线叫圆的割线,这两个公共点叫交点.
(3)直线和圆没有公共点时,叫做
直线和圆相离.
·
·
·
1. 画一个圆,移动你手中的直尺,如果把这个直尺看成一条直线,那么这条直线和圆有几种位置关系?并画出图形。
2.判断直线和圆的位置关系方法:
(1)由上可知,从___________________________判断直线和圆的位置关系.
直线和圆公共点的个数
探究
上述变化过程中,除了公共点的个数发生了变化,还有什么量在改变?你能否用数量关系来判别直线与圆的位置关系?
(1).点到直线的距离:
点O到直线l的距离是指________________________________________________________.
(2).设⊙O的半径为r,圆心O到直线l的距离为d,请模仿点和圆的位置关系,总结出以下结论:
①直线l和⊙O相交 ___________;
②直线l和⊙O相切 ___________;
③直线l和⊙O相离 ___________;
连接直线外一点与直线上各点的所有线段中,垂线段最短,这条垂线段的长度,叫做点到直线的距离。
直线与圆的位置关系:
0
d>r
1
d=r
切点
切线
2
d
割线
.O
l
d
r
┐
┐
.o
l
d
r
.O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由 _______________ 的个数来判断;
(2)由_________________
的大小关系来判断。
两
直线与圆的公共点
圆心到直线的距离d与半径r
归纳:
如图:已知∠ AOB=30°,M为OB上一点,且OM=5cm,以M为圆心,以r为半径的圆与直线OA有怎样的位置关系?为什么?
(1)r=2cm; (2)r=4cm; (3)r=2.5cm.
解:过点M作MN⊥OA于点N
∵在Rt△OMN中,∠AOB=30°,OM=5cm. ∴MN=2.5CM
即圆心M到直线OA的距离d=2.5cm
(1)当r=2cm时, ∵d> r,
∴⊙M与直线OA相离。
(2)当r=4cm时, ∵d< r,
∴⊙M与直线OA相交。
(3)当r=2.5cm时, ∵d = r,
∴⊙M与直线OA相切。
做一做
2.5cm
开动脑筋
练一练
1.已知圆的直径为14cm,圆心到直线的距离为d,当d =9 cm时,直线和圆 ;当d =7 cm时,直线和圆 ;当d <6 cm时,直线和圆
2.已知⊙O的半径为5 cm,直线l上有一点B到圆心O的距离等于5 cm,则直线l和⊙O的位置关系是( ) .
A.相离 B.相切 C.相交 D.不能确定
相离
相切
相交
已知Rt△ABC的斜边AB=10cm,AC=6cm.画图说明
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切
(2)以点C为圆心,分别以4cm和5 cm的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系
思考:判断直线与圆位置关系的方法有哪些?
归纳: 根据(1)定义;(2)d与r的大小关系。
思考?
知识链接:
1.点O与直线m的距离为d,⊙O 的半径为r,若d,r是方程
的两个根,则直线m与⊙O的位置关系是 ______ 。
2.若d,r是方程 的两个根,且直线m与⊙O的位置关系是相切,则a的值是 。
3.如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,开始时,PO=6cm.如果⊙P以1cm/秒的速度沿由A向B的方向移动,那么当⊙P的运动时间t(秒)满足条件()时,⊙P与直线CD相交.
当堂检测
1、设⊙O的半径为4,点O到直线a的距离为d,
若⊙O与直线a至多只有一个公共点,则d为…( )
A、d≤4 B、d<4 C、d≥4 D、d=4
2、设⊙p的半径为4cm,直线l上一点A到圆心的
距离为4cm,则直线l与⊙O的位置关系
是……………………………………………( )
A、相交 B、相切 C、相离 D、相切或相交
C
D
当堂检测
3.⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l与⊙O没有公共点,则d为( )
A.d >3 B.d<3 C.d ≤3 D.d =3
4.圆心O到直线的距离等于⊙O的半径,则直线和⊙O的位置关系是( )
A.相离 B.相交 C.相切 D.相切或相交
A
C
5.已知⊙O的直径是10㎝,点O到直线L距离为d,若 直线L与⊙O相切,则d= ( )
A.d=10 B.d=5 C.d>5 D.d<5
B
6.直线L 和⊙O有公共点,则直线L与⊙O ( )
A.相离 B.相切 C.相交 D.相切或相交
D
7.判断:若直线和圆相切,则该直线和圆一定有一个公共点.( )
√
8.等边三角形ABC的边长为2,则以A为圆心,半径为1.7的圆与直线BC的位置关系是 ,以A为圆心,以 为半径的圆与直线BC相切.
相离
当堂检测
在Rt△ABC中,∠C=90°,
AC=3cm,BC=4cm,
以C为圆心,r为半径作圆。
想一想
当r满足___________
_______________ 时,⊙C与线段AB只有一个公共点.
r=2.4cm
B
C
A
D
4
5
3
d=2.4cm
或3cm
(1)一种是根据定义进行识别:
直线L与⊙o没有公共点 直线L与⊙o相离。
直线L与⊙o只有一个公共点 直线L与⊙o相切。
直线L与⊙o有两个公共点 直线L与⊙o相交。
(2)另一种是根据圆心到直线的距离d与圆半径r数量
比较来进行识别:
d>r 直线L与⊙o相离;
d=r 直线L与⊙o相切;
d
课堂小结
同课章节目录
