北师大版数学七下5.3.1简单的轴对称图形课件(共20张PPT)
文档属性
| 名称 | 北师大版数学七下5.3.1简单的轴对称图形课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-19 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
5.3简单的轴对称图形(1)
学习五环闯关
1
1.激活思维
2
2.探究新知
3
3.双基巩固
4
4.综合运用
5
5.分层反馈
一.激活思维
激活思维
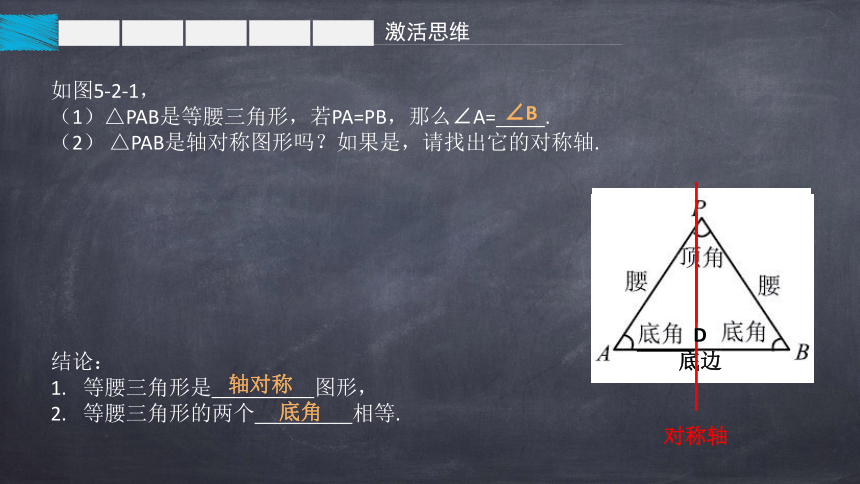
如图5-2-1,
(1)△PAB是等腰三角形,若PA=PB,那么∠A= .
(2) △PAB是轴对称图形吗?如果是,请找出它的对称轴.
∠B
结论:
等腰三角形是 图形,
等腰三角形的两个 相等.
底角
轴对称
对称轴
底边
D
二.探究新知
探究新知
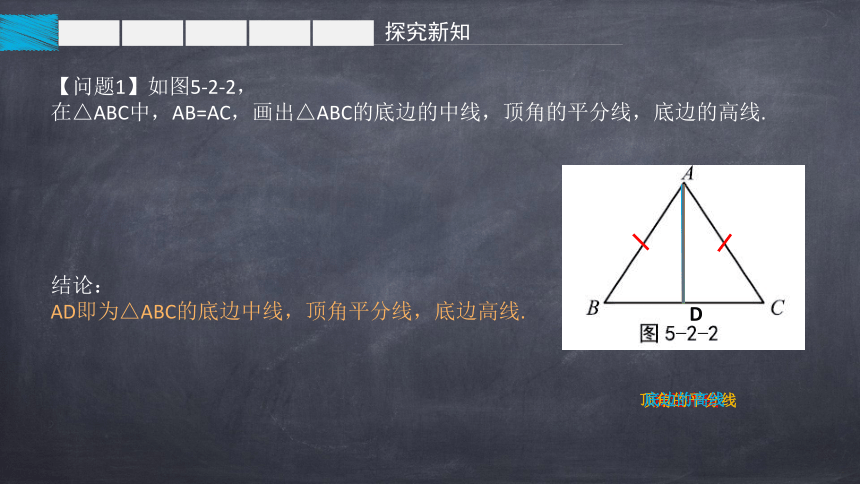
【问题1】如图5-2-2,
在△ABC中,AB=AC,画出△ABC的底边的中线,顶角的平分线,底边的高线.
底边中线
顶角的平分线
底边的高线
结论:
AD即为△ABC的底边中线,顶角平分线,底边高线.
D
探究新知
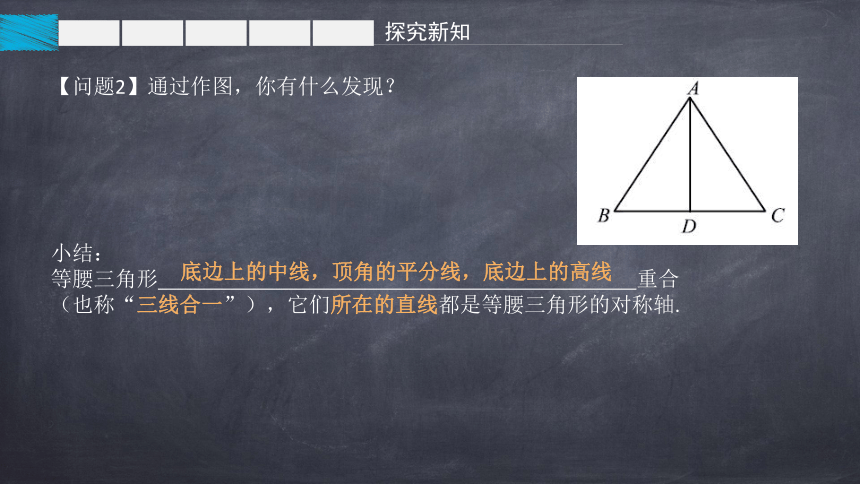
【问题2】通过作图,你有什么发现?
小结:
等腰三角形 重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
底边上的中线,顶角的平分线,底边上的高线
探究知识小结
等腰三角形是轴对称图形,
等腰三角形的两个底角相等,
等腰三角形底边上的中线,顶角的平分线,底边上的高线
重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
三.双基巩固
双基巩固
【例题1】
(1)已知等腰△ABC中,∠A=90° ,则其余两角的度数是?请说明理由.
(2)已知等腰△ABC中,∠A=100° ,则其余两角的度数是?请说明理由.
(3)已知等腰△ABC中,∠A=30° ,则其余两角的度数是?请说明理由.
四.综合应用
综合应用
【例题2】如图5-2-3,AD是等边△ABC的中线,在AC边上截取AE=AD,求
∠EDC的度数.
30°
解题方法小结
在解决等腰三角形的问题时,
1.等腰三角形的两个腰相等,两个底角相等,在给出其中一个角度的时候,
如果顶角为∠α,则底角为 (180°- α)°
如果底角为∠α,则顶角为 (180°- 2α) °
0°< 顶角度数 <180°
0°< 底角度数 <90°
2.如果等腰三角形中出现了底边的中线,顶角的平分线,底边的高线,要尝试利用等腰三角形的三线合一解决问题.
注意:如果题目中给出的角度没有说明是顶角还是底角时,要考虑两种情况
五.分层反馈
分层反馈
1.(1)等腰三角形的一个底角为40 °,则此等腰三角形的顶角为 ;
(2)一个等角三角形有一个角为110 °,则另外两个角为 ;
(3)一个等腰三角形有一个角为40 °,则另外两个角为 ;
2. 下列图形中,不是轴对称图形的是 ( )
A. 有两个内角相等的三角形
B. 有一个内角是45°的直角三角形
C. 有一个内角是30°的直角三角形
D. 有两个角分别是30°和120°的三角形
分层反馈
3. 如图5-2-4,在△ABC中,已知AB=AC,D是BC边上的中点,∠B=30 °,求∠BAC和
∠ADC的度数.
分层反馈
4. 如图5-2-5,在△ABC中AB=AC,AB的垂直平分线MN交AC于点D.
(1)若∠A=38 °,则∠DBC= .
(2)若AC+BC=10cm,则△DBC的周长为 ,请说明理由.
分层反馈
5. 如图5-2-6所示,要在街道旁边修一个奶站,向居民区AB提供牛奶,奶站应该建在
什么地方才能使它到A,B的距离之和最短.
谢谢您的聆听
5.3简单的轴对称图形(1)
学习五环闯关
1
1.激活思维
2
2.探究新知
3
3.双基巩固
4
4.综合运用
5
5.分层反馈
一.激活思维
激活思维
如图5-2-1,
(1)△PAB是等腰三角形,若PA=PB,那么∠A= .
(2) △PAB是轴对称图形吗?如果是,请找出它的对称轴.
∠B
结论:
等腰三角形是 图形,
等腰三角形的两个 相等.
底角
轴对称
对称轴
底边
D
二.探究新知
探究新知
【问题1】如图5-2-2,
在△ABC中,AB=AC,画出△ABC的底边的中线,顶角的平分线,底边的高线.
底边中线
顶角的平分线
底边的高线
结论:
AD即为△ABC的底边中线,顶角平分线,底边高线.
D
探究新知
【问题2】通过作图,你有什么发现?
小结:
等腰三角形 重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
底边上的中线,顶角的平分线,底边上的高线
探究知识小结
等腰三角形是轴对称图形,
等腰三角形的两个底角相等,
等腰三角形底边上的中线,顶角的平分线,底边上的高线
重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
三.双基巩固
双基巩固
【例题1】
(1)已知等腰△ABC中,∠A=90° ,则其余两角的度数是?请说明理由.
(2)已知等腰△ABC中,∠A=100° ,则其余两角的度数是?请说明理由.
(3)已知等腰△ABC中,∠A=30° ,则其余两角的度数是?请说明理由.
四.综合应用
综合应用
【例题2】如图5-2-3,AD是等边△ABC的中线,在AC边上截取AE=AD,求
∠EDC的度数.
30°
解题方法小结
在解决等腰三角形的问题时,
1.等腰三角形的两个腰相等,两个底角相等,在给出其中一个角度的时候,
如果顶角为∠α,则底角为 (180°- α)°
如果底角为∠α,则顶角为 (180°- 2α) °
0°< 顶角度数 <180°
0°< 底角度数 <90°
2.如果等腰三角形中出现了底边的中线,顶角的平分线,底边的高线,要尝试利用等腰三角形的三线合一解决问题.
注意:如果题目中给出的角度没有说明是顶角还是底角时,要考虑两种情况
五.分层反馈
分层反馈
1.(1)等腰三角形的一个底角为40 °,则此等腰三角形的顶角为 ;
(2)一个等角三角形有一个角为110 °,则另外两个角为 ;
(3)一个等腰三角形有一个角为40 °,则另外两个角为 ;
2. 下列图形中,不是轴对称图形的是 ( )
A. 有两个内角相等的三角形
B. 有一个内角是45°的直角三角形
C. 有一个内角是30°的直角三角形
D. 有两个角分别是30°和120°的三角形
分层反馈
3. 如图5-2-4,在△ABC中,已知AB=AC,D是BC边上的中点,∠B=30 °,求∠BAC和
∠ADC的度数.
分层反馈
4. 如图5-2-5,在△ABC中AB=AC,AB的垂直平分线MN交AC于点D.
(1)若∠A=38 °,则∠DBC= .
(2)若AC+BC=10cm,则△DBC的周长为 ,请说明理由.
分层反馈
5. 如图5-2-6所示,要在街道旁边修一个奶站,向居民区AB提供牛奶,奶站应该建在
什么地方才能使它到A,B的距离之和最短.
谢谢您的聆听
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
