27.1.1 相似图形及成比例线段 同步练习(含答案)
文档属性
| 名称 | 27.1.1 相似图形及成比例线段 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 16:46:00 | ||
图片预览




文档简介
27.1 图形的相似
第1课时 相似图形及成比例线段
一、选择题
1.相似图形是( )
A.形状相同的图形 B.大小不相同的图形 C.能够重合的图形 D.大小相同的图形
2.在下列图形中,相似的一组是( )
3.下列说法正确的是( )
A.小红小学毕业时的照片和初中毕业时的照片相似
B.商店新买来的一副三角板是相似的
C.所有的课本都是相似的
D.国旗上的五角星都是相似的
4.下列不相似的是( )
A.同一张底片冲洗出来的两张大小不同的照片
B.粘在投影仪镜头上的标签投出的不同的像
C.某人的侧身照片和正面照片
D.比例为1∶10的C929模型和C929远程宽体客机
5.已知线段a,b,c,d满足ab=cd,把它改写成比例式,错误的是( )
A.a∶d=c∶b B.a∶b=c∶d C.d∶a=b∶c D.a∶c=d∶b
6.已知南京地铁十号线一期工程的长度是21.6 km,则在比例尺是1∶40 000的工程示意图上,它的长度是( )
A.5.4 cm B.54 cm C.540 cm D.0.54 cm
7.下列四组图形中,其中一个图形可以看作由另一个图形放大或缩小得到的是( )
8.已知线段a=4,b=16,线段c是线段a,b的比例中项,那么c等于( )
A.10 B.8 C.-8 D.±8
9.若===k,则k的值为( )
A.2 B.-1 C.2或-1 D.不存在
10.将直角三角形的三条边的长度都扩大同样的倍数后得到的三角形( )
A.仍是直角三角形 B.一定是锐角三角形 C.可能是钝角三角形 D.一定是钝角三角形
11.若某个直角三角形的两直角边之比为2∶3,则确定了该三角形的( )
A.形状 B.周长 C.面积 D.斜边
12.下列形状分别为正方形、矩形、正三角形、圆,其中不一定是相似图形的是( )
13.已知三个数2,,4.如果再添加一个数,使这四个数成比例,则添加的数是( )
A.2 B.2或
C.2,4或8 D.2,或4
二、填空题
14.给出下列几何图形:①两个正方形;②两个平行四边形;③两个正六边形;④两个等腰三角形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中一定相似的有 .(填序号)
15.已知a,b,c,d是成比例线段,其中a=5 cm,b=3 cm,c=6 cm,则线段d=____cm.
16.【2020·湘潭】若=,则=________.
17.【2021·大庆】已知===0.145,则=________.
18.如图,在长8 cm,宽4 cm的矩形中截去一个矩形(阴影部分),使留下的矩形与原矩形相似,那么留下的矩形的面积为____cm2.
第18题图 第19题图 第20题图
19.如图,相似的正方形共有________个,相似的三角形共有________个.
三、解答题
20.某课外活动小组的同学在研究某种植物标本(如图)时,测得叶片①的最大宽度是8 cm,最大长度是16 cm;叶片②的最大宽度是7 cm,最大长度是14 cm;叶片③的最大宽度约为6.5 cm.请你用所学数学知识估算叶片③的完整叶片的最大长度约为多少
21.已知图中的两个梯形相似,求未知边x,y,z的长度和∠α,∠β的度数.
22.如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,△ACB和△DCE的顶点都在格点上.请问:AC,AB,CD,DE是成比例线段吗?请说明理由.
23.已知线段a,b,c满足==,且a+2b+c=26.
(1)求线段a,b,c的长;
(2)若线段x是线段a,b的比例中项,求x.
24.已知a,b,c是△ABC的三边长,且(a-c) ∶(a+b) ∶(c-b)=(-2) ∶7 ∶1,a+b+c=24.
(1)求a,b,c的值;
(2)判断△ABC的形状.
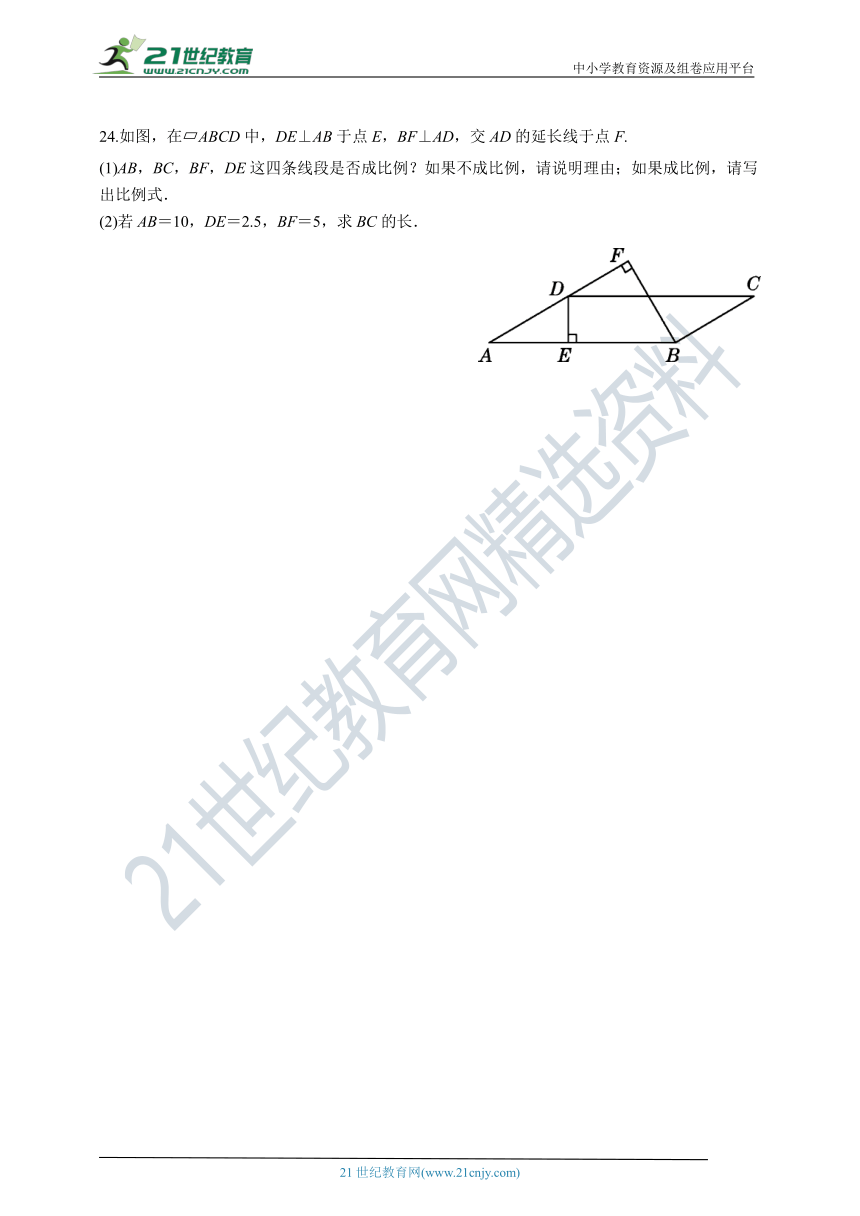
24.如图,在 ABCD中,DE⊥AB于点E,BF⊥AD,交AD的延长线于点F.
(1)AB,BC,BF,DE这四条线段是否成比例?如果不成比例,请说明理由;如果成比例,请写出比例式.
(2)若AB=10,DE=2.5,BF=5,求BC的长.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.相似图形是( A )
A.形状相同的图形 B.大小不相同的图形 C.能够重合的图形 D.大小相同的图形
2.在下列图形中,相似的一组是( C )
3.下列说法正确的是( D )
A.小红小学毕业时的照片和初中毕业时的照片相似
B.商店新买来的一副三角板是相似的
C.所有的课本都是相似的
D.国旗上的五角星都是相似的
4.下列不相似的是( C )
A.同一张底片冲洗出来的两张大小不同的照片
B.粘在投影仪镜头上的标签投出的不同的像
C.某人的侧身照片和正面照片
D.比例为1∶10的C929模型和C929远程宽体客机
5.已知线段a,b,c,d满足ab=cd,把它改写成比例式,错误的是( B )
A.a∶d=c∶b B.a∶b=c∶d C.d∶a=b∶c D.a∶c=d∶b
6.已知南京地铁十号线一期工程的长度是21.6 km,则在比例尺是1∶40 000的工程示意图上,它的长度是( B )
A.5.4 cm B.54 cm C.540 cm D.0.54 cm
7.下列四组图形中,其中一个图形可以看作由另一个图形放大或缩小得到的是( B )
8.已知线段a=4,b=16,线段c是线段a,b的比例中项,那么c等于( B )
A.10 B.8 C.-8 D.±8
9.若===k,则k的值为( C )
A.2 B.-1 C.2或-1 D.不存在
【点拨】分情况讨论:当a+b+c≠0时,根据等比性质,得k==2;当a+b+c=0时,a+b=-c,所以k=-1.
10.将直角三角形的三条边的长度都扩大同样的倍数后得到的三角形( A )
A.仍是直角三角形 B.一定是锐角三角形 C.可能是钝角三角形 D.一定是钝角三角形
11.若某个直角三角形的两直角边之比为2∶3,则确定了该三角形的( A )
A.形状 B.周长 C.面积 D.斜边
12.下列形状分别为正方形、矩形、正三角形、圆,其中不一定是相似图形的是( B )
13.已知三个数2,,4.如果再添加一个数,使这四个数成比例,则添加的数是( D )
A.2 B.2或
C.2,4或8 D.2,或4
【点拨】本题易忽略线段成比例的顺序性而漏解.四条线段成比例时,要把这四条线段按顺序排列,不能随意颠倒.
二、填空题
14.给出下列几何图形:①两个正方形;②两个平行四边形;③两个正六边形;④两个等腰三角形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中一定相似的有 .(填序号)
【答案】①③⑤
15.已知a,b,c,d是成比例线段,其中a=5 cm,b=3 cm,c=6 cm,则线段d=____cm.
【答案】
16.【2020·湘潭】若=,则=________.
【答案】
17.【2021·大庆】已知===0.145,则=________.
【答案】
18.如图,在长8 cm,宽4 cm的矩形中截去一个矩形(阴影部分),使留下的矩形与原矩形相似,那么留下的矩形的面积为____cm2.
【答案】8
第18题图 第19题图 第20题图
19.如图,相似的正方形共有________个,相似的三角形共有________个.
【答案】5 16
三、解答题
20.某课外活动小组的同学在研究某种植物标本(如图)时,测得叶片①的最大宽度是8 cm,最大长度是16 cm;叶片②的最大宽度是7 cm,最大长度是14 cm;叶片③的最大宽度约为6.5 cm.请你用所学数学知识估算叶片③的完整叶片的最大长度约为多少
解:根据叶片①②的最大长度和宽度,可得出这种植物的叶片的最大宽度∶最大长度=1∶2,由此估算出完整的叶片③的最大长度是6.5×2=13 cm.
21.已知图中的两个梯形相似,求未知边x,y,z的长度和∠α,∠β的度数.
解:∵两个梯形相似,∴===,解得x=3,y=6,z=3.
∵相似多边形的对应角相等,∴∠α=∠D=180°-∠A=180°-62°=118°,
∠β=∠B′=180°-∠C′=180°-110°=70°
22.如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,△ACB和△DCE的顶点都在格点上.请问:AC,AB,CD,DE是成比例线段吗?请说明理由.
解:AC,AB,CD,DE是成比例线段.
理由:由题意得AC=3,CD=2,
AB===3,
DE===2.
∴==.
∴AC,AB,CD,DE是成比例线段.
23.已知线段a,b,c满足==,且a+2b+c=26.
(1)求线段a,b,c的长;
解:设===k,
∴a=3k,b=2k,c=6k.
∵a+2b+c=26,∴3k+4k+6k=26,
解得k=2.
∴a=6,b=4,c=12.
(2)若线段x是线段a,b的比例中项,求x.
解:∵线段x是线段a,b的比例中项,
∴x2=ab.
又∵a=6,b=4,
∴x=2(负值舍去).
24.已知a,b,c是△ABC的三边长,且(a-c) ∶(a+b) ∶(c-b)=(-2) ∶7 ∶1,a+b+c=24.
(1)求a,b,c的值;
解:∵(a-c)∶(a+b) ∶(c-b)=(-2) ∶7∶1,
∴设===k(k≠0).
∴解得
∵a+b+c=24,
∴3k+4k+5k=24,解得k=2.
∴a=6,b=8,c=10.
(2)判断△ABC的形状.
解:∵a2+b2=62+82=102=c2,
∴△ABC是直角三角形.
24.如图,在 ABCD中,DE⊥AB于点E,BF⊥AD,交AD的延长线于点F.
(1)AB,BC,BF,DE这四条线段是否成比例?如果不成比例,请说明理由;如果成比例,请写出比例式.
【思路点拨】利用面积法(即S ABCD不变)建立等式,即可判断是否成比例.
解:∵在 ABCD中,DE⊥AB,BF⊥AD,
∴S ABCD=AB·DE=AD·BF.
∵AD=BC,∴AB·DE=BC·BF,即=.
∴AB,BC,BF,DE这四条线段成比例,比例式为=.
(2)若AB=10,DE=2.5,BF=5,求BC的长.
解:∵AB·DE=BC·BF,
∴10×2.5=5BC,
解得BC=5.
第1课时 相似图形及成比例线段
一、选择题
1.相似图形是( )
A.形状相同的图形 B.大小不相同的图形 C.能够重合的图形 D.大小相同的图形
2.在下列图形中,相似的一组是( )
3.下列说法正确的是( )
A.小红小学毕业时的照片和初中毕业时的照片相似
B.商店新买来的一副三角板是相似的
C.所有的课本都是相似的
D.国旗上的五角星都是相似的
4.下列不相似的是( )
A.同一张底片冲洗出来的两张大小不同的照片
B.粘在投影仪镜头上的标签投出的不同的像
C.某人的侧身照片和正面照片
D.比例为1∶10的C929模型和C929远程宽体客机
5.已知线段a,b,c,d满足ab=cd,把它改写成比例式,错误的是( )
A.a∶d=c∶b B.a∶b=c∶d C.d∶a=b∶c D.a∶c=d∶b
6.已知南京地铁十号线一期工程的长度是21.6 km,则在比例尺是1∶40 000的工程示意图上,它的长度是( )
A.5.4 cm B.54 cm C.540 cm D.0.54 cm
7.下列四组图形中,其中一个图形可以看作由另一个图形放大或缩小得到的是( )
8.已知线段a=4,b=16,线段c是线段a,b的比例中项,那么c等于( )
A.10 B.8 C.-8 D.±8
9.若===k,则k的值为( )
A.2 B.-1 C.2或-1 D.不存在
10.将直角三角形的三条边的长度都扩大同样的倍数后得到的三角形( )
A.仍是直角三角形 B.一定是锐角三角形 C.可能是钝角三角形 D.一定是钝角三角形
11.若某个直角三角形的两直角边之比为2∶3,则确定了该三角形的( )
A.形状 B.周长 C.面积 D.斜边
12.下列形状分别为正方形、矩形、正三角形、圆,其中不一定是相似图形的是( )
13.已知三个数2,,4.如果再添加一个数,使这四个数成比例,则添加的数是( )
A.2 B.2或
C.2,4或8 D.2,或4
二、填空题
14.给出下列几何图形:①两个正方形;②两个平行四边形;③两个正六边形;④两个等腰三角形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中一定相似的有 .(填序号)
15.已知a,b,c,d是成比例线段,其中a=5 cm,b=3 cm,c=6 cm,则线段d=____cm.
16.【2020·湘潭】若=,则=________.
17.【2021·大庆】已知===0.145,则=________.
18.如图,在长8 cm,宽4 cm的矩形中截去一个矩形(阴影部分),使留下的矩形与原矩形相似,那么留下的矩形的面积为____cm2.
第18题图 第19题图 第20题图
19.如图,相似的正方形共有________个,相似的三角形共有________个.
三、解答题
20.某课外活动小组的同学在研究某种植物标本(如图)时,测得叶片①的最大宽度是8 cm,最大长度是16 cm;叶片②的最大宽度是7 cm,最大长度是14 cm;叶片③的最大宽度约为6.5 cm.请你用所学数学知识估算叶片③的完整叶片的最大长度约为多少
21.已知图中的两个梯形相似,求未知边x,y,z的长度和∠α,∠β的度数.
22.如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,△ACB和△DCE的顶点都在格点上.请问:AC,AB,CD,DE是成比例线段吗?请说明理由.
23.已知线段a,b,c满足==,且a+2b+c=26.
(1)求线段a,b,c的长;
(2)若线段x是线段a,b的比例中项,求x.
24.已知a,b,c是△ABC的三边长,且(a-c) ∶(a+b) ∶(c-b)=(-2) ∶7 ∶1,a+b+c=24.
(1)求a,b,c的值;
(2)判断△ABC的形状.
24.如图,在 ABCD中,DE⊥AB于点E,BF⊥AD,交AD的延长线于点F.
(1)AB,BC,BF,DE这四条线段是否成比例?如果不成比例,请说明理由;如果成比例,请写出比例式.
(2)若AB=10,DE=2.5,BF=5,求BC的长.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.相似图形是( A )
A.形状相同的图形 B.大小不相同的图形 C.能够重合的图形 D.大小相同的图形
2.在下列图形中,相似的一组是( C )
3.下列说法正确的是( D )
A.小红小学毕业时的照片和初中毕业时的照片相似
B.商店新买来的一副三角板是相似的
C.所有的课本都是相似的
D.国旗上的五角星都是相似的
4.下列不相似的是( C )
A.同一张底片冲洗出来的两张大小不同的照片
B.粘在投影仪镜头上的标签投出的不同的像
C.某人的侧身照片和正面照片
D.比例为1∶10的C929模型和C929远程宽体客机
5.已知线段a,b,c,d满足ab=cd,把它改写成比例式,错误的是( B )
A.a∶d=c∶b B.a∶b=c∶d C.d∶a=b∶c D.a∶c=d∶b
6.已知南京地铁十号线一期工程的长度是21.6 km,则在比例尺是1∶40 000的工程示意图上,它的长度是( B )
A.5.4 cm B.54 cm C.540 cm D.0.54 cm
7.下列四组图形中,其中一个图形可以看作由另一个图形放大或缩小得到的是( B )
8.已知线段a=4,b=16,线段c是线段a,b的比例中项,那么c等于( B )
A.10 B.8 C.-8 D.±8
9.若===k,则k的值为( C )
A.2 B.-1 C.2或-1 D.不存在
【点拨】分情况讨论:当a+b+c≠0时,根据等比性质,得k==2;当a+b+c=0时,a+b=-c,所以k=-1.
10.将直角三角形的三条边的长度都扩大同样的倍数后得到的三角形( A )
A.仍是直角三角形 B.一定是锐角三角形 C.可能是钝角三角形 D.一定是钝角三角形
11.若某个直角三角形的两直角边之比为2∶3,则确定了该三角形的( A )
A.形状 B.周长 C.面积 D.斜边
12.下列形状分别为正方形、矩形、正三角形、圆,其中不一定是相似图形的是( B )
13.已知三个数2,,4.如果再添加一个数,使这四个数成比例,则添加的数是( D )
A.2 B.2或
C.2,4或8 D.2,或4
【点拨】本题易忽略线段成比例的顺序性而漏解.四条线段成比例时,要把这四条线段按顺序排列,不能随意颠倒.
二、填空题
14.给出下列几何图形:①两个正方形;②两个平行四边形;③两个正六边形;④两个等腰三角形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中一定相似的有 .(填序号)
【答案】①③⑤
15.已知a,b,c,d是成比例线段,其中a=5 cm,b=3 cm,c=6 cm,则线段d=____cm.
【答案】
16.【2020·湘潭】若=,则=________.
【答案】
17.【2021·大庆】已知===0.145,则=________.
【答案】
18.如图,在长8 cm,宽4 cm的矩形中截去一个矩形(阴影部分),使留下的矩形与原矩形相似,那么留下的矩形的面积为____cm2.
【答案】8
第18题图 第19题图 第20题图
19.如图,相似的正方形共有________个,相似的三角形共有________个.
【答案】5 16
三、解答题
20.某课外活动小组的同学在研究某种植物标本(如图)时,测得叶片①的最大宽度是8 cm,最大长度是16 cm;叶片②的最大宽度是7 cm,最大长度是14 cm;叶片③的最大宽度约为6.5 cm.请你用所学数学知识估算叶片③的完整叶片的最大长度约为多少
解:根据叶片①②的最大长度和宽度,可得出这种植物的叶片的最大宽度∶最大长度=1∶2,由此估算出完整的叶片③的最大长度是6.5×2=13 cm.
21.已知图中的两个梯形相似,求未知边x,y,z的长度和∠α,∠β的度数.
解:∵两个梯形相似,∴===,解得x=3,y=6,z=3.
∵相似多边形的对应角相等,∴∠α=∠D=180°-∠A=180°-62°=118°,
∠β=∠B′=180°-∠C′=180°-110°=70°
22.如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,△ACB和△DCE的顶点都在格点上.请问:AC,AB,CD,DE是成比例线段吗?请说明理由.
解:AC,AB,CD,DE是成比例线段.
理由:由题意得AC=3,CD=2,
AB===3,
DE===2.
∴==.
∴AC,AB,CD,DE是成比例线段.
23.已知线段a,b,c满足==,且a+2b+c=26.
(1)求线段a,b,c的长;
解:设===k,
∴a=3k,b=2k,c=6k.
∵a+2b+c=26,∴3k+4k+6k=26,
解得k=2.
∴a=6,b=4,c=12.
(2)若线段x是线段a,b的比例中项,求x.
解:∵线段x是线段a,b的比例中项,
∴x2=ab.
又∵a=6,b=4,
∴x=2(负值舍去).
24.已知a,b,c是△ABC的三边长,且(a-c) ∶(a+b) ∶(c-b)=(-2) ∶7 ∶1,a+b+c=24.
(1)求a,b,c的值;
解:∵(a-c)∶(a+b) ∶(c-b)=(-2) ∶7∶1,
∴设===k(k≠0).
∴解得
∵a+b+c=24,
∴3k+4k+5k=24,解得k=2.
∴a=6,b=8,c=10.
(2)判断△ABC的形状.
解:∵a2+b2=62+82=102=c2,
∴△ABC是直角三角形.
24.如图,在 ABCD中,DE⊥AB于点E,BF⊥AD,交AD的延长线于点F.
(1)AB,BC,BF,DE这四条线段是否成比例?如果不成比例,请说明理由;如果成比例,请写出比例式.
【思路点拨】利用面积法(即S ABCD不变)建立等式,即可判断是否成比例.
解:∵在 ABCD中,DE⊥AB,BF⊥AD,
∴S ABCD=AB·DE=AD·BF.
∵AD=BC,∴AB·DE=BC·BF,即=.
∴AB,BC,BF,DE这四条线段成比例,比例式为=.
(2)若AB=10,DE=2.5,BF=5,求BC的长.
解:∵AB·DE=BC·BF,
∴10×2.5=5BC,
解得BC=5.
