27.2.1.1 平行线分线段成比例 同步练习(含答案)
文档属性
| 名称 | 27.2.1.1 平行线分线段成比例 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 16:46:00 | ||
图片预览




文档简介
27.2 相似三角形
27.2.1 相似三角形的判定
第2课时 平行线分线段成比例
一、选择题
1.如图,△ABC∽△ADE,则下列比例式正确的是( )
A.= B.= C.= D.=
第1题图 第2题图 第3题图 第4题图
2.如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( )
A.2 B.2 C.2 D.4
3.如图,已知AB∥CD∥EF,那么下列结论正确的是( )
A.= B.= C.= D.=
4.如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若AB=3,DE=2,BC=6,则EF的值为( )
A.1 B.2 C.3 D.4
5.【2021·哈尔滨】如图,在△ABC中,DE∥BC,AD=2,BD=3,AC=10,则AE的长为( )
A.3 B.4 C.5 D.6
第5题图 第6题图 第7题图 第8题图
6.【中考·恩施州】如图,在 ABCD中,EF∥AB交BD于F,交AD于E.DE∶EA=3∶4,EF=3,则CD的长是( )
A.4 B.7 C.3 D.12
7.【2020·哈尔滨】如图,在△ABC中,点D在BC边上,连接AD,点E在AC边上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是( )
A.= B.= C.= D.=
8.【中考·潍坊】如图,点E是 ABCD的边AD上的一点,且=,连接BE并延长交CD的延长线于点F,若DE=3,DF=4,则 ABCD的周长为( )
A.21 B.28 C.34 D.42
9.如图,在平行四边形ABCD中,点E,F分别在边AD,BC上,且EF∥CD,G为边AD延长线上一点,连接BG,则图中与△ABG相似的三角形有( )
A.1个 B.2个 C.3个 D.4个
第9题图 第10题图 第11题图 第12题图
10.如图,AD∥BC,在△ABC中,点E在AB边上,EF∥BC,交AC边于点F,DE交AC边于点G,则下列结论错误的是( )
A. B. C. D.
11.如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则DF∶FC=( )
A.1∶4 B.1∶3 C.1∶2 D.1∶1
12.【中考·凉山州】如图,在△ABC中,D在AC边上,AD ∶DC=1 ∶2,O是BD的中点,连接AO并延长交BC于E,则BE ∶EC=( )
A.1∶2 B.1∶3 C.1∶4 D.2∶3
二、填空题
13.若△ABC∽△A'B'C',△ABC与△A'B'C'的相似比为2,那么△A'B'C'与△ABC的相似比为 .
14.(1)如图,l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,过点B的直线DE分别交l1,l3于点D,E.若AB=2,BC=4,BD=3,则线段BE的长为 .
(2)如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A,B,C和点D,E,F.若OA=1,OB=2,BC=4,EF=5,则DE的值为 .
第14(1)题图 第14(2)题图 第15题图 第16题图
15.如图,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AD与BC相交于点E,EF⊥BD,垂足为F.试回答:图中△DEF∽ ,△BEF∽ ,△ABE∽ .
16.如图,在△ABC中,若DE∥BC,EF∥CD,AE=2EC,则AF∶FD∶DB= .
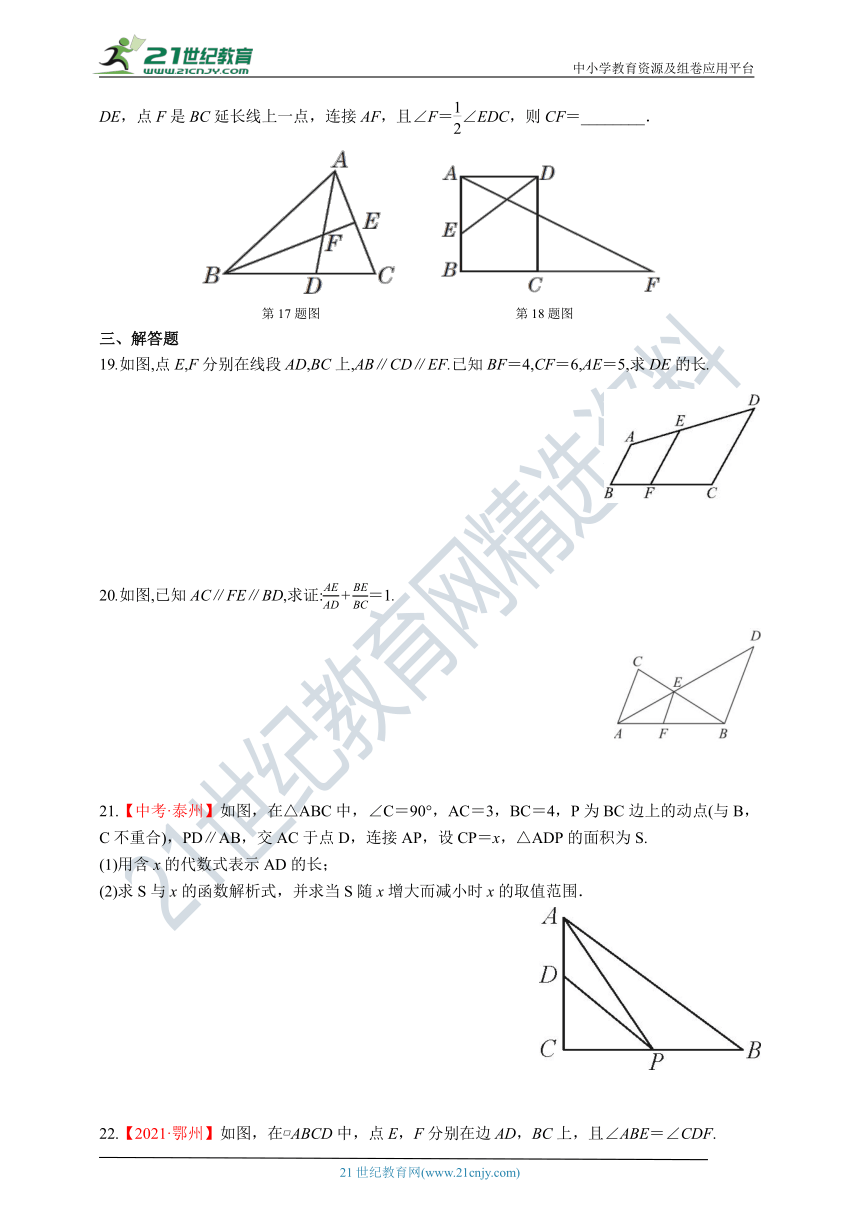
17.【2021·连云港】如图,BE是△ABC的中线,点F在BE上,连接AF并延长交BC于点D.若BF=3FE,则=________.
18.【2021·营口】如图,矩形ABCD中,AB=5,BC=4,点E是AB边上一点,AE=3,连接DE,点F是BC延长线上一点,连接AF,且∠F=∠EDC,则CF=________.
第17题图 第18题图
三、解答题
19.如图,点E,F分别在线段AD,BC上,AB∥CD∥EF.已知BF=4,CF=6,AE=5,求DE的长.
20.如图,已知AC∥FE∥BD,求证:=1.
21.【中考·泰州】如图,在△ABC中,∠C=90°,AC=3,BC=4,P为BC边上的动点(与B,C不重合),PD∥AB,交AC于点D,连接AP,设CP=x,△ADP的面积为S.
(1)用含x的代数式表示AD的长;
(2)求S与x的函数解析式,并求当S随x增大而减小时x的取值范围.
22.【2021·鄂州】如图,在 ABCD中,点E,F分别在边AD,BC上,且∠ABE=∠CDF.
(1)探究四边形BEDF的形状,并说明理由;
(2)连接AC,分别交BE,DF于点G,H,连接BD交AC于点O.若=,AE=4,求BC的长.
23.如图,O是△ABC内任意一点,DE∥AB,DF∥AC,EF∥BC,那么△ABC与△DEF相似吗 说明理由.
24.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理:如图1,在△ABC中,AD平分∠BAC,则.下面是这个定理的部分证明过程.
证明:如图2,过点C作CE∥AD,交BA的延长线于点E……
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)如图3,在Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,求△ABD的周长.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图,△ABC∽△ADE,则下列比例式正确的是( D )
A.= B.= C.= D.=
第1题图 第2题图 第3题图 第4题图
2.如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( B )
A.2 B.2 C.2 D.4
3.如图,已知AB∥CD∥EF,那么下列结论正确的是( A )
A.= B.= C.= D.=
4.如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若AB=3,DE=2,BC=6,则EF的值为( D )
A.1 B.2 C.3 D.4
5.【2021·哈尔滨】如图,在△ABC中,DE∥BC,AD=2,BD=3,AC=10,则AE的长为( B )
A.3 B.4 C.5 D.6
第5题图 第6题图 第7题图 第8题图
6.【中考·恩施州】如图,在 ABCD中,EF∥AB交BD于F,交AD于E.DE∶EA=3∶4,EF=3,则CD的长是( B )
A.4 B.7 C.3 D.12
7.【2020·哈尔滨】如图,在△ABC中,点D在BC边上,连接AD,点E在AC边上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是( C )
A.= B.= C.= D.=
8.【中考·潍坊】如图,点E是 ABCD的边AD上的一点,且=,连接BE并延长交CD的延长线于点F,若DE=3,DF=4,则 ABCD的周长为( C )
A.21 B.28 C.34 D.42
9.如图,在平行四边形ABCD中,点E,F分别在边AD,BC上,且EF∥CD,G为边AD延长线上一点,连接BG,则图中与△ABG相似的三角形有( D )
A.1个 B.2个 C.3个 D.4个
第9题图 第10题图 第11题图 第12题图
10.如图,AD∥BC,在△ABC中,点E在AB边上,EF∥BC,交AC边于点F,DE交AC边于点G,则下列结论错误的是( C )
A. B. C. D.
11.如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则DF∶FC=( C )
A.1∶4 B.1∶3 C.1∶2 D.1∶1
12.【中考·凉山州】如图,在△ABC中,D在AC边上,AD ∶DC=1 ∶2,O是BD的中点,连接AO并延长交BC于E,则BE ∶EC=( B )
A.1 ∶2 B.1 ∶3 C.1 ∶4 D.2 ∶3
【点拨】过点O作OG∥BC,交AC于点G.
∵O是BD的中点,∴G是DC的中点.
∵AD∶DC=1∶2,∴AD=DG=GC.
∴AG∶GC=2∶1.∴AO∶OE=2∶1.
∴S△AOB∶S△BOE=2∶1.
设S△BOE=S,S△AOB=2S,
又BO=OD,∴S△AOD=2S.∴S△ABD=4S.
∴S△BDC=2S△ABD=8S. ∴S四边形CDOE=7S.∴S△AEC=9S.
又∵S△ABE=3S,∴===.
二、填空题
13.若△ABC∽△A'B'C',△ABC与△A'B'C'的相似比为2,那么△A'B'C'与△ABC的相似比为 (或1∶2) .
14.(1)如图,l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,过点B的直线DE分别交l1,l3于点D,E.若AB=2,BC=4,BD=3,则线段BE的长为 6 .
(2)如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A,B,C和点D,E,F.若OA=1,OB=2,BC=4,EF=5,则DE的值为 .
第14(1)题图 第14(2)题图 第15题图 第16题图
15.如图,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AD与BC相交于点E,EF⊥BD,垂足为F.试回答:图中△DEF∽ △DAB ,△BEF∽ △BCD ,△ABE∽ △DCE .
16.如图,在△ABC中,若DE∥BC,EF∥CD,AE=2EC,则AF∶FD∶DB= 4∶2∶3 .
17.【2021·连云港】如图,BE是△ABC的中线,点F在BE上,连接AF并延长交BC于点D.若BF=3FE,则=________.
【答案】
第17题图 第18题图
18.【2021·营口】如图,矩形ABCD中,AB=5,BC=4,点E是AB边上一点,AE=3,连接DE,点F是BC延长线上一点,连接AF,且∠F=∠EDC,则CF=________.
【点拨】如图,连接EC,过点D作DH⊥EC于H.
∵四边形ABCD是矩形,
∴∠BAD=∠BCD=90°,AD=BC=4,AB=CD=5.
∵AE=3,
∴DE===5,
∴DE=DC.
∵DH⊥EC,∴∠CDH=∠EDH,∴∠CDH=∠EDC.
∵∠F=∠EDC,∴∠CDH=∠F.
∵∠BCE+∠DCH=90°,∠DCH+∠CDH=90°,
∴∠BCE=∠CDH,
∴∠BCE=∠F,∴EC∥AF,
∴=,即=,∴CF=6.
【答案】6
三、解答题
19.如图,点E,F分别在线段AD,BC上,AB∥CD∥EF.已知BF=4,CF=6,AE=5,求DE的长.
解:∵AB∥CD∥EF,
∴.
20.如图,已知AC∥FE∥BD,求证:=1.
证明:∵AC∥EF,∴. ①
∵FE∥BD,∴. ②
②+①,得=1.
21.【中考·泰州】如图,在△ABC中,∠C=90°,AC=3,BC=4,P为BC边上的动点(与B,C不重合),PD∥AB,交AC于点D,连接AP,设CP=x,△ADP的面积为S.
(1)用含x的代数式表示AD的长;
(2)求S与x的函数解析式,并求当S随x增大而减小时x的取值范围.
解:(1)∵PD∥AB,∴=,∵AC=3,BC=4,CP=x,∴=,
∴CD=x,∴AD=AC-CD=3-x,即AD=-x+3
(2)根据题意得S=AD·CP=×(-x+3)x=-(x-2)2+,
∴当x≥2时,S随x的增大而减小,又∵0<x<4,
∴当S随x增大而减小时,x的取值范围为2≤x<4
22.【2021·鄂州】如图,在 ABCD中,点E,F分别在边AD,BC上,且∠ABE=∠CDF.
(1)探究四边形BEDF的形状,并说明理由;
解:四边形BEDF为平行四边形,理由如下:
∵四边形ABCD为平行四边形,∴∠ABC=∠ADC.
∵∠ABE=∠CDF,∴∠EBF=∠EDF.
∵四边形ABCD为平行四边形,∴AD∥BC.
∴∠EDF=∠DFC=∠EBF.∴BE∥DF.
∵AD∥BC,
∴四边形BEDF为平行四边形.
(2)连接AC,分别交BE,DF于点G,H,连接BD交AC于点O.若=,AE=4,求BC的长.
解:设AG=2a,∵=,∴OG=3a,AO=5a.
∵四边形ABCD为平行四边形,
∴AO=CO=5a,∴CG=8a.
∵AD∥BC,∴△AGE∽△CGB.∴==.
∵AE=4,∴BC=16.
23.如图,O是△ABC内任意一点,DE∥AB,DF∥AC,EF∥BC,那么△ABC与△DEF相似吗 说明理由.
解:△ABC∽△DEF.
理由:∵DE∥AB,∴△ODE∽△OAB,
∴∠ODE=∠OAB,∠OED=∠OBA,.
同理可证∠ODF=∠OAC,∠OFD=∠OCA,∠OEF=∠OBC,∠OFE=∠OCB,,
∴∠EDF=∠BAC,∠DEF=∠ABC,∠DFE=∠ACB,,∴△ABC∽△DEF.
24.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理:如图1,在△ABC中,AD平分∠BAC,则.下面是这个定理的部分证明过程.
证明:如图2,过点C作CE∥AD,交BA的延长线于点E……
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)如图3,在Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,求△ABD的周长.
解:(1)∵CE∥AD,∴,∠2=∠ACE,∠1=∠E.
∵AD平分∠BAC,∴∠1=∠2,∴∠ACE=∠E,
∴AE=AC,∴.
(2)∵AB=3,BC=4,∠ABC=90°,∴AC=5.
∵AD平分∠BAC,∴,
∴BD=,
∴AD=,
∴△ABD的周长=.
27.2.1 相似三角形的判定
第2课时 平行线分线段成比例
一、选择题
1.如图,△ABC∽△ADE,则下列比例式正确的是( )
A.= B.= C.= D.=
第1题图 第2题图 第3题图 第4题图
2.如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( )
A.2 B.2 C.2 D.4
3.如图,已知AB∥CD∥EF,那么下列结论正确的是( )
A.= B.= C.= D.=
4.如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若AB=3,DE=2,BC=6,则EF的值为( )
A.1 B.2 C.3 D.4
5.【2021·哈尔滨】如图,在△ABC中,DE∥BC,AD=2,BD=3,AC=10,则AE的长为( )
A.3 B.4 C.5 D.6
第5题图 第6题图 第7题图 第8题图
6.【中考·恩施州】如图,在 ABCD中,EF∥AB交BD于F,交AD于E.DE∶EA=3∶4,EF=3,则CD的长是( )
A.4 B.7 C.3 D.12
7.【2020·哈尔滨】如图,在△ABC中,点D在BC边上,连接AD,点E在AC边上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是( )
A.= B.= C.= D.=
8.【中考·潍坊】如图,点E是 ABCD的边AD上的一点,且=,连接BE并延长交CD的延长线于点F,若DE=3,DF=4,则 ABCD的周长为( )
A.21 B.28 C.34 D.42
9.如图,在平行四边形ABCD中,点E,F分别在边AD,BC上,且EF∥CD,G为边AD延长线上一点,连接BG,则图中与△ABG相似的三角形有( )
A.1个 B.2个 C.3个 D.4个
第9题图 第10题图 第11题图 第12题图
10.如图,AD∥BC,在△ABC中,点E在AB边上,EF∥BC,交AC边于点F,DE交AC边于点G,则下列结论错误的是( )
A. B. C. D.
11.如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则DF∶FC=( )
A.1∶4 B.1∶3 C.1∶2 D.1∶1
12.【中考·凉山州】如图,在△ABC中,D在AC边上,AD ∶DC=1 ∶2,O是BD的中点,连接AO并延长交BC于E,则BE ∶EC=( )
A.1∶2 B.1∶3 C.1∶4 D.2∶3
二、填空题
13.若△ABC∽△A'B'C',△ABC与△A'B'C'的相似比为2,那么△A'B'C'与△ABC的相似比为 .
14.(1)如图,l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,过点B的直线DE分别交l1,l3于点D,E.若AB=2,BC=4,BD=3,则线段BE的长为 .
(2)如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A,B,C和点D,E,F.若OA=1,OB=2,BC=4,EF=5,则DE的值为 .
第14(1)题图 第14(2)题图 第15题图 第16题图
15.如图,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AD与BC相交于点E,EF⊥BD,垂足为F.试回答:图中△DEF∽ ,△BEF∽ ,△ABE∽ .
16.如图,在△ABC中,若DE∥BC,EF∥CD,AE=2EC,则AF∶FD∶DB= .
17.【2021·连云港】如图,BE是△ABC的中线,点F在BE上,连接AF并延长交BC于点D.若BF=3FE,则=________.
18.【2021·营口】如图,矩形ABCD中,AB=5,BC=4,点E是AB边上一点,AE=3,连接DE,点F是BC延长线上一点,连接AF,且∠F=∠EDC,则CF=________.
第17题图 第18题图
三、解答题
19.如图,点E,F分别在线段AD,BC上,AB∥CD∥EF.已知BF=4,CF=6,AE=5,求DE的长.
20.如图,已知AC∥FE∥BD,求证:=1.
21.【中考·泰州】如图,在△ABC中,∠C=90°,AC=3,BC=4,P为BC边上的动点(与B,C不重合),PD∥AB,交AC于点D,连接AP,设CP=x,△ADP的面积为S.
(1)用含x的代数式表示AD的长;
(2)求S与x的函数解析式,并求当S随x增大而减小时x的取值范围.
22.【2021·鄂州】如图,在 ABCD中,点E,F分别在边AD,BC上,且∠ABE=∠CDF.
(1)探究四边形BEDF的形状,并说明理由;
(2)连接AC,分别交BE,DF于点G,H,连接BD交AC于点O.若=,AE=4,求BC的长.
23.如图,O是△ABC内任意一点,DE∥AB,DF∥AC,EF∥BC,那么△ABC与△DEF相似吗 说明理由.
24.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理:如图1,在△ABC中,AD平分∠BAC,则.下面是这个定理的部分证明过程.
证明:如图2,过点C作CE∥AD,交BA的延长线于点E……
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)如图3,在Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,求△ABD的周长.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图,△ABC∽△ADE,则下列比例式正确的是( D )
A.= B.= C.= D.=
第1题图 第2题图 第3题图 第4题图
2.如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( B )
A.2 B.2 C.2 D.4
3.如图,已知AB∥CD∥EF,那么下列结论正确的是( A )
A.= B.= C.= D.=
4.如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若AB=3,DE=2,BC=6,则EF的值为( D )
A.1 B.2 C.3 D.4
5.【2021·哈尔滨】如图,在△ABC中,DE∥BC,AD=2,BD=3,AC=10,则AE的长为( B )
A.3 B.4 C.5 D.6
第5题图 第6题图 第7题图 第8题图
6.【中考·恩施州】如图,在 ABCD中,EF∥AB交BD于F,交AD于E.DE∶EA=3∶4,EF=3,则CD的长是( B )
A.4 B.7 C.3 D.12
7.【2020·哈尔滨】如图,在△ABC中,点D在BC边上,连接AD,点E在AC边上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是( C )
A.= B.= C.= D.=
8.【中考·潍坊】如图,点E是 ABCD的边AD上的一点,且=,连接BE并延长交CD的延长线于点F,若DE=3,DF=4,则 ABCD的周长为( C )
A.21 B.28 C.34 D.42
9.如图,在平行四边形ABCD中,点E,F分别在边AD,BC上,且EF∥CD,G为边AD延长线上一点,连接BG,则图中与△ABG相似的三角形有( D )
A.1个 B.2个 C.3个 D.4个
第9题图 第10题图 第11题图 第12题图
10.如图,AD∥BC,在△ABC中,点E在AB边上,EF∥BC,交AC边于点F,DE交AC边于点G,则下列结论错误的是( C )
A. B. C. D.
11.如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则DF∶FC=( C )
A.1∶4 B.1∶3 C.1∶2 D.1∶1
12.【中考·凉山州】如图,在△ABC中,D在AC边上,AD ∶DC=1 ∶2,O是BD的中点,连接AO并延长交BC于E,则BE ∶EC=( B )
A.1 ∶2 B.1 ∶3 C.1 ∶4 D.2 ∶3
【点拨】过点O作OG∥BC,交AC于点G.
∵O是BD的中点,∴G是DC的中点.
∵AD∶DC=1∶2,∴AD=DG=GC.
∴AG∶GC=2∶1.∴AO∶OE=2∶1.
∴S△AOB∶S△BOE=2∶1.
设S△BOE=S,S△AOB=2S,
又BO=OD,∴S△AOD=2S.∴S△ABD=4S.
∴S△BDC=2S△ABD=8S. ∴S四边形CDOE=7S.∴S△AEC=9S.
又∵S△ABE=3S,∴===.
二、填空题
13.若△ABC∽△A'B'C',△ABC与△A'B'C'的相似比为2,那么△A'B'C'与△ABC的相似比为 (或1∶2) .
14.(1)如图,l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,过点B的直线DE分别交l1,l3于点D,E.若AB=2,BC=4,BD=3,则线段BE的长为 6 .
(2)如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A,B,C和点D,E,F.若OA=1,OB=2,BC=4,EF=5,则DE的值为 .
第14(1)题图 第14(2)题图 第15题图 第16题图
15.如图,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AD与BC相交于点E,EF⊥BD,垂足为F.试回答:图中△DEF∽ △DAB ,△BEF∽ △BCD ,△ABE∽ △DCE .
16.如图,在△ABC中,若DE∥BC,EF∥CD,AE=2EC,则AF∶FD∶DB= 4∶2∶3 .
17.【2021·连云港】如图,BE是△ABC的中线,点F在BE上,连接AF并延长交BC于点D.若BF=3FE,则=________.
【答案】
第17题图 第18题图
18.【2021·营口】如图,矩形ABCD中,AB=5,BC=4,点E是AB边上一点,AE=3,连接DE,点F是BC延长线上一点,连接AF,且∠F=∠EDC,则CF=________.
【点拨】如图,连接EC,过点D作DH⊥EC于H.
∵四边形ABCD是矩形,
∴∠BAD=∠BCD=90°,AD=BC=4,AB=CD=5.
∵AE=3,
∴DE===5,
∴DE=DC.
∵DH⊥EC,∴∠CDH=∠EDH,∴∠CDH=∠EDC.
∵∠F=∠EDC,∴∠CDH=∠F.
∵∠BCE+∠DCH=90°,∠DCH+∠CDH=90°,
∴∠BCE=∠CDH,
∴∠BCE=∠F,∴EC∥AF,
∴=,即=,∴CF=6.
【答案】6
三、解答题
19.如图,点E,F分别在线段AD,BC上,AB∥CD∥EF.已知BF=4,CF=6,AE=5,求DE的长.
解:∵AB∥CD∥EF,
∴.
20.如图,已知AC∥FE∥BD,求证:=1.
证明:∵AC∥EF,∴. ①
∵FE∥BD,∴. ②
②+①,得=1.
21.【中考·泰州】如图,在△ABC中,∠C=90°,AC=3,BC=4,P为BC边上的动点(与B,C不重合),PD∥AB,交AC于点D,连接AP,设CP=x,△ADP的面积为S.
(1)用含x的代数式表示AD的长;
(2)求S与x的函数解析式,并求当S随x增大而减小时x的取值范围.
解:(1)∵PD∥AB,∴=,∵AC=3,BC=4,CP=x,∴=,
∴CD=x,∴AD=AC-CD=3-x,即AD=-x+3
(2)根据题意得S=AD·CP=×(-x+3)x=-(x-2)2+,
∴当x≥2时,S随x的增大而减小,又∵0<x<4,
∴当S随x增大而减小时,x的取值范围为2≤x<4
22.【2021·鄂州】如图,在 ABCD中,点E,F分别在边AD,BC上,且∠ABE=∠CDF.
(1)探究四边形BEDF的形状,并说明理由;
解:四边形BEDF为平行四边形,理由如下:
∵四边形ABCD为平行四边形,∴∠ABC=∠ADC.
∵∠ABE=∠CDF,∴∠EBF=∠EDF.
∵四边形ABCD为平行四边形,∴AD∥BC.
∴∠EDF=∠DFC=∠EBF.∴BE∥DF.
∵AD∥BC,
∴四边形BEDF为平行四边形.
(2)连接AC,分别交BE,DF于点G,H,连接BD交AC于点O.若=,AE=4,求BC的长.
解:设AG=2a,∵=,∴OG=3a,AO=5a.
∵四边形ABCD为平行四边形,
∴AO=CO=5a,∴CG=8a.
∵AD∥BC,∴△AGE∽△CGB.∴==.
∵AE=4,∴BC=16.
23.如图,O是△ABC内任意一点,DE∥AB,DF∥AC,EF∥BC,那么△ABC与△DEF相似吗 说明理由.
解:△ABC∽△DEF.
理由:∵DE∥AB,∴△ODE∽△OAB,
∴∠ODE=∠OAB,∠OED=∠OBA,.
同理可证∠ODF=∠OAC,∠OFD=∠OCA,∠OEF=∠OBC,∠OFE=∠OCB,,
∴∠EDF=∠BAC,∠DEF=∠ABC,∠DFE=∠ACB,,∴△ABC∽△DEF.
24.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理:如图1,在△ABC中,AD平分∠BAC,则.下面是这个定理的部分证明过程.
证明:如图2,过点C作CE∥AD,交BA的延长线于点E……
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)如图3,在Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,求△ABD的周长.
解:(1)∵CE∥AD,∴,∠2=∠ACE,∠1=∠E.
∵AD平分∠BAC,∴∠1=∠2,∴∠ACE=∠E,
∴AE=AC,∴.
(2)∵AB=3,BC=4,∠ABC=90°,∴AC=5.
∵AD平分∠BAC,∴,
∴BD=,
∴AD=,
∴△ABD的周长=.
