27.2.1.2 用平行线判定三角形相似 同步练习(含答案)
文档属性
| 名称 | 27.2.1.2 用平行线判定三角形相似 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 00:00:00 | ||
图片预览




文档简介
27.2 相似三角形
27.2.1 相似三角形的判定
第2课时 用平行线判定三角形相似
一、选择题
1.如图,AB∥CD∥EF,则图中相似三角形有( )
A.0对 B.3对 C.2对 D.1对
第1题图 第2题图 第3题图 第4题图
2.【中考·河南】如图,在△ABC中,点D,E分别是AB,AC的中点,则下列结论:①BC=2DE;②△ADE∽△ABC;③=.其中正确的有( )
A.3个 B.2个 C.1个 D.0个
3.如图,已知BC交AD于点E,AB∥EF∥CD,那么下列结论中不成立的是( )
A.△DEF∽△DAB B.△BEF∽△BCD C.△BEF∽△DCE D.△ABE∽△DCE
4.【中考·玉林】如图,AB∥EF∥DC,AD∥BC,EF与AC交于点G,则相似三角形共有( )
A.3对 B.5对 C.6对 D.8对
5.如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
A.= B.= C.= D.=
第5题图 第6题图 第7题图 第8题图
6.问题:“如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,DF∥AC,求证:△ADE∽△DBF.”某同学的证明过程如下:
证明:①又∵DF∥AC;②∵DE∥BC;③∴△ADE∽△ABC;④∴△DBF∽△ABC;⑤∴△ADE∽△DBF.
步骤正确的顺序是( )
A.③②④①⑤ B.⑤②④①③ C.①③④②⑤ D.②③①④⑤
7.如图,在 ABCD中,点E在AD上,EC交对角线BD于点F,AE∶ED=2∶1,则EF∶FC等于( )
A.1∶1 B.1∶2 C.1∶3 D.2∶3
8.【2021·淄博】如图,AB,CD相交于点E,且AC∥EF∥DB,点C,F,B在同一条直线上,已知AC=p,EF=r,DB=q,则p,q,r之间满足的数量关系式是( )
A.+= B.+= C.+= D.+=
9.【中考·杭州】如图,在△ABC中,点D,E分别在AB和AC边上,DE∥BC,M为BC边上一点(不与点B,C重合),连接AM交DE于点N,则( )
A.= B.= C.= D.=
第9题图 第10题图 第11题图 第12题图
10.【2019·安徽】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G.若EF=EG,则CD的长为( )
A.3.6 B.4 C.4.8 D.5
11.【2020·遂宁】如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G.若AF=2FD,则的值为( )
A. B. C. D.
12.如图,AD是△ABC的中线,点E在AD上,AD=4DE,连接BE并延长,交AC于点F,则AF∶FC的值是( )
A.3∶2 B.4∶3 C.2∶1 D.2∶3
二、填空题
13.如图,在△ABC中,DE∥BC,GF∥AC,GF,DE相交于M点,则图中与△ABC相似的三角形有________个.
第13题图 第14题图 第15题图 第16题图
14.如图,在△ABC中,点D,E分别在AB,AC上,DE∥BC.若AD=4,DB=2,BC=6,则DE的值为________.
15.如图所示是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120 m,DC=60 m,EC=50 m,求得河宽AB= m.
16.【盐城中考】如图,BC∥DE,且BC<DE,AD=BC=4,AB+DE=10.则的值为____.
17.【2020·临沂】如图,在△ABC中,D,E为边AB的三等分点,EF∥DG∥AC,H为AF与DG的交点.若AC=6,则DH=________.
第17题图 第18题图
18.如图,已知在Rt△ABC中,∠C=90°,正方形DCEF的顶点D,E,F分别在边AC,BC,AB上,如果AC=10,BC=6,那么正方形DCEF的周长为________.
三、解答题
19.如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若=,DE=4,求BC的长.
20.如图,DE∥BC,分别交AB,AC于点D,E,连接BE,CD,交于点O.
(1)写出图中的相似三角形;
(2)求证=.
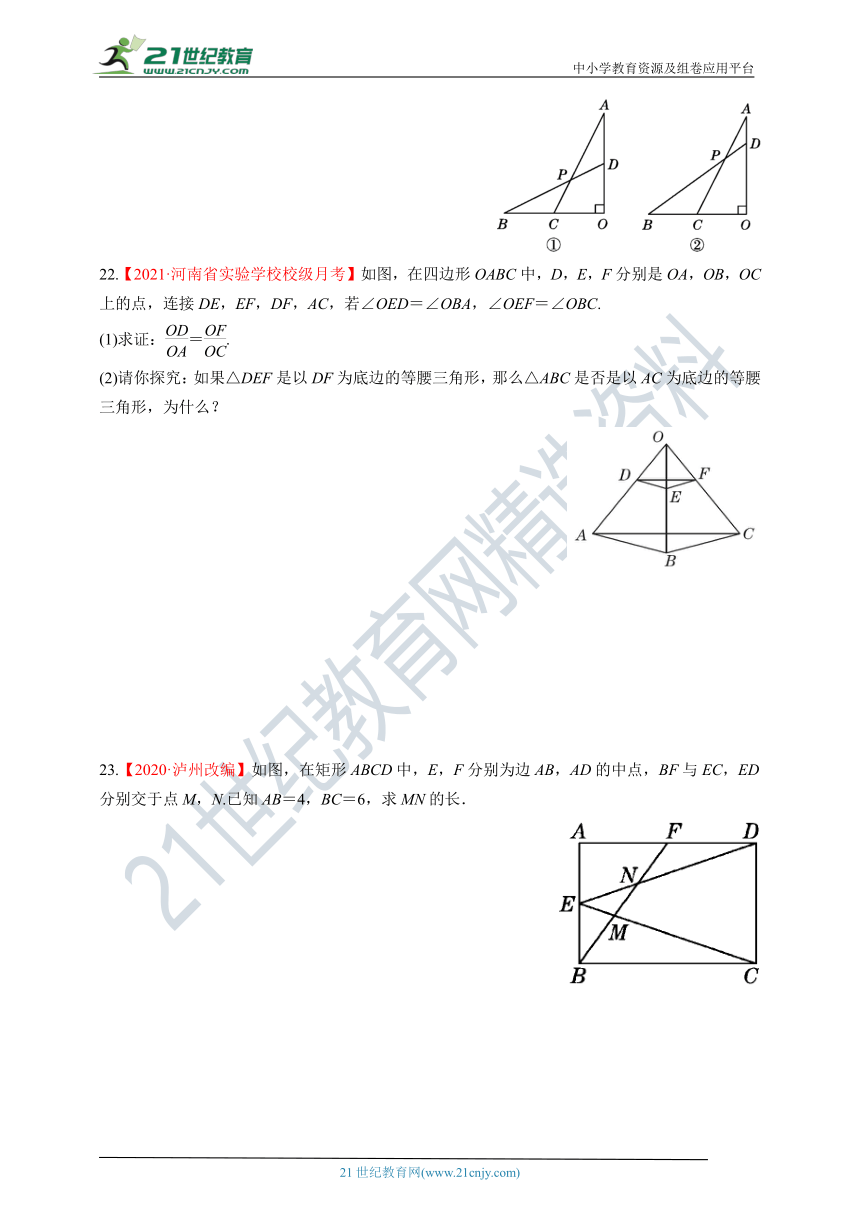
21.已知线段OA⊥OB,点C为OB的中点,点D为AO上一点,连接AC,BD交于点P.
(1)如图①,当点D为AO的中点时,求的值;
(2)如图②,当=时,求的值.
22.【2021·河南省实验学校校级月考】如图,在四边形OABC中,D,E,F分别是OA,OB,OC上的点,连接DE,EF,DF,AC,若∠OED=∠OBA,∠OEF=∠OBC.
(1)求证:=.
(2)请你探究:如果△DEF是以DF为底边的等腰三角形,那么△ABC是否是以AC为底边的等腰三角形,为什么?
23.【2020·泸州改编】如图,在矩形ABCD中,E,F分别为边AB,AD的中点,BF与EC,ED分别交于点M,N.已知AB=4,BC=6,求MN的长.
24.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ.点P,Q分别从点A,C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)直接用含t的式子表示:QB=__________,PD=__________;
(2)是否存在t值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由,并探究如何改变点Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图,AB∥CD∥EF,则图中相似三角形有( B )
A.0对 B.3对 C.2对 D.1对
第1题图 第2题图 第3题图 第4题图
2.【中考·河南】如图,在△ABC中,点D,E分别是AB,AC的中点,则下列结论:①BC=2DE;②△ADE∽△ABC;③=.其中正确的有( A )
A.3个 B.2个 C.1个 D.0个
3.如图,已知BC交AD于点E,AB∥EF∥CD,那么下列结论中不成立的是( C )
A.△DEF∽△DAB B.△BEF∽△BCD C.△BEF∽△DCE D.△ABE∽△DCE
4.【中考·玉林】如图,AB∥EF∥DC,AD∥BC,EF与AC交于点G,则相似三角形共有( C )
A.3对 B.5对 C.6对 D.8对
【点拨】图中三角形有△AEG,△ADC,△CFG,△CBA.由AB∥EF∥DC,AD∥BC,易得△AEG∽△ADC∽△CFG∽△CBA,有6种组合,则相似三角形共有6对.
5.如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( C )
A.= B.= C.= D.=
第5题图 第6题图 第7题图 第8题图
6.问题:“如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,DF∥AC,求证:△ADE∽△DBF.”某同学的证明过程如下:
证明:①又∵DF∥AC;②∵DE∥BC;③∴△ADE∽△ABC;④∴△DBF∽△ABC;⑤∴△ADE∽△DBF.
步骤正确的顺序是( D )
A.③②④①⑤ B.⑤②④①③ C.①③④②⑤ D.②③①④⑤
7.如图,在 ABCD中,点E在AD上,EC交对角线BD于点F,AE∶ED=2∶1,则EF∶FC等于( C )
A.1∶1 B.1∶2 C.1∶3 D.2∶3
8.【2021·淄博】如图,AB,CD相交于点E,且AC∥EF∥DB,点C,F,B在同一条直线上,已知AC=p,EF=r,DB=q,则p,q,r之间满足的数量关系式是( )
A.+= B.+= C.+= D.+=
【点拨】EF∥AC,∴△BEF∽△BAC.∴=.
∵EF∥DB,∴△CEF∽△CDB.∴=.
∴+=+===1,即+=1.
∴+=.
【答案】C
9.【中考·杭州】如图,在△ABC中,点D,E分别在AB和AC边上,DE∥BC,M为BC边上一点(不与点B,C重合),连接AM交DE于点N,则( C )
A.= B.= C.= D.=
第9题图 第10题图 第11题图 第12题图
10.【2019·安徽】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G.若EF=EG,则CD的长为( B )
A.3.6 B.4 C.4.8 D.5
【点拨】如图,作DH∥EG交AB于点H,则△AEG∽△ADH.∴=.
∵EF⊥AC,∠C=90°,∴∠EFA=∠C=90°.
∴EF∥CD.∴△AEF∽△ADC.
∴=∴=.
∵EG=EF,∴DH=CD.
设DH=x,则CD=x.
∵BC=12,AC=6,∴BD=12-x.
∵EF⊥AC,EF⊥EG,DH∥EG,
∴EG∥AC∥DH.∴△BDH∽△BCA.
∴=,即=,解得x=4,∴CD=4.
11.【2020·遂宁】如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G.若AF=2FD,则的值为( )
A. B. C. D.
【点拨】设FD=k,则AF=2k,AD=3k.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD.
∴∠AFB=∠FBC=∠DFG,∠ABF=∠G.
∵BE平分∠ABC,∴∠ABF=∠FBC.
∴∠ABF=∠AFB=∠DFG=∠G.
∴AB=AF=2k,FD=DG=k.
∴CD=2k.
∴CG=CD+DG=3k.
∵AB∥CG,
∴△ABE∽△CGE.
∴===.
【答案】C
12.如图,AD是△ABC的中线,点E在AD上,AD=4DE,连接BE并延长,交AC于点F,则AF∶FC的值是( A )
A.3∶2 B.4∶3 C.2∶1 D.2∶3
【提示】过点D作DG∥AC,与BF交于点G,因此FC=2DG,AF=3DG.
二、填空题
13.如图,在△ABC中,DE∥BC,GF∥AC,GF,DE相交于M点,则图中与△ABC相似的三角形有________个.
【答案】3
第13题图 第14题图 第15题图 第16题图
14.如图,在△ABC中,点D,E分别在AB,AC上,DE∥BC.若AD=4,DB=2,BC=6,则DE的值为________.
【答案】4
15.如图所示是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120 m,DC=60 m,EC=50 m,求得河宽AB= m.
【答案】100
16.【盐城中考】如图,BC∥DE,且BC<DE,AD=BC=4,AB+DE=10.则的值为____.
【答案】2
17.【2020·临沂】如图,在△ABC中,D,E为边AB的三等分点,EF∥DG∥AC,H为AF与DG的交点.若AC=6,则DH=________.
【答案】1
第17题图 第18题图
18.如图,已知在Rt△ABC中,∠C=90°,正方形DCEF的顶点D,E,F分别在边AC,BC,AB上,如果AC=10,BC=6,那么正方形DCEF的周长为________.
【点拨】∵四边形DCEF为正方形,∴DF∥BC,DC=DF,
∴△ADF∽△ACB,∴=,设DC=x,则DF=x,
AD=10-x,∴=,解得x=,
∴正方形DCEF的周长为4×=15.
【答案】15
三、解答题
19.如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若=,DE=4,求BC的长.
解:∵=,∴=.
∵DE∥BC,∴△ADE∽△ABC.
∴==,即=,解得BC=6.
20.如图,DE∥BC,分别交AB,AC于点D,E,连接BE,CD,交于点O.
(1)写出图中的相似三角形;
解:△ADE∽△ABC,△DOE∽△COB.
(2)求证=.
证明:由(1)知△ADE∽△ABC,∴=.
又由(1)知△DOE∽△COB,∴=.
∴=.
21.已知线段OA⊥OB,点C为OB的中点,点D为AO上一点,连接AC,BD交于点P.
(1)如图①,当点D为AO的中点时,求的值;
解:如图①,过点C作CE∥OA,交BD于点E,
∴△BCE∽△BOD.
∴==. ∴CE=OD=AD.
∵CE∥OA,∴△ECP∽△DAP.
∴===2.
(2)如图②,当=时,求的值.
【思路点拨】过一点作平行于三角形一边的线段,构造相似三角形来解决以上两题.12题过AC边的中点E作平行于CD的线段;13题以AP,PC为三角形的对应边,通过作平行线构造相似三角形.
解:如图②,过点C作CE∥OA,交BD于点E,
∴△BCE∽△BOD,∴==.
设AD=x,则OA=4x,OD=3x.∴CE=OD=x.
由OA∥CE得△DAP∽△ECP,
∴===. ∴=.
22.【2021·河南省实验学校校级月考】如图,在四边形OABC中,D,E,F分别是OA,OB,OC上的点,连接DE,EF,DF,AC,若∠OED=∠OBA,∠OEF=∠OBC.
(1)求证:=.
证明:∵∠OED=∠OBA,∠OEF=∠OBC,
∴DE∥AB,EF∥BC.
由DE∥AB,
得△ODE∽△OAB,
∴=.
由EF∥BC,得△OFE∽△OCB,
∴=.∴=.
(2)请你探究:如果△DEF是以DF为底边的等腰三角形,那么△ABC是否是以AC为底边的等腰三角形,为什么?
解:是.理由如下:由△OFE∽△OCB,
得=.
由△ODE∽△OAB,得=.∴=.
∵△DEF是以DF为底边的等腰三角形,
∴DE=EF,
∴AB=BC,即△ABC是以AC为底边的等腰三角形.
23.【2020·泸州改编】如图,在矩形ABCD中,E,F分别为边AB,AD的中点,BF与EC,ED分别交于点M,N.已知AB=4,BC=6,求MN的长.
解:如图,过点E作EH∥AD,交BF于点G,交CD于点H,
∴△BEG∽△BAF,∴=.
∵AB=4,BC=6,E为AB的中点,F为AD的中点,
∴BE=2,AF=DF=3,∴=,∴EG=.
由题意易得△EGN∽△DFN,△EGM∽△CBM,
∴=,=,
∴=,=,即=,=,
∴2NG=NF,4MG=MB.
∵E为AB的中点,EH∥AD,∴G为BF的中点,
∴BG=GF=BF= =,
∴NG=GF=,MG=BG=,
∴MN=NG+MG=.
24.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ.点P,Q分别从点A,C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)直接用含t的式子表示:QB=__________,PD=__________;
【答案】8-2t t
(2)是否存在t值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由,并探究如何改变点Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形.
解:不存在.理由如下:
在Rt△ABC中,∠C=90°,AC=6,BC=8,
∴AB=10.
∵PD∥BC,∴△APD∽△ACB,
∴=,即=,∴AD=t.
∴BD=AB-AD=10-t.
∵BQ∥DP,
∴当BQ=DP时,四边形PDBQ是平行四边形,
即8-2t=t,解得t=.
当t=时,PD=×=,BD=10-×=6,
∴DP≠BD,∴四边形PDBQ不能为菱形.
设点Q的速度为每秒v个单位长度时满足条件,则BQ=8-vt,PD=t,BD=10-t.要使四边形PDBQ为菱形,则PD=BD=BQ.
∴t=10-t=8-vt,解得t=,v=.
∴当点Q的速度为每秒个单位长度时,经过秒,四边形PDBQ为菱形.
27.2.1 相似三角形的判定
第2课时 用平行线判定三角形相似
一、选择题
1.如图,AB∥CD∥EF,则图中相似三角形有( )
A.0对 B.3对 C.2对 D.1对
第1题图 第2题图 第3题图 第4题图
2.【中考·河南】如图,在△ABC中,点D,E分别是AB,AC的中点,则下列结论:①BC=2DE;②△ADE∽△ABC;③=.其中正确的有( )
A.3个 B.2个 C.1个 D.0个
3.如图,已知BC交AD于点E,AB∥EF∥CD,那么下列结论中不成立的是( )
A.△DEF∽△DAB B.△BEF∽△BCD C.△BEF∽△DCE D.△ABE∽△DCE
4.【中考·玉林】如图,AB∥EF∥DC,AD∥BC,EF与AC交于点G,则相似三角形共有( )
A.3对 B.5对 C.6对 D.8对
5.如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
A.= B.= C.= D.=
第5题图 第6题图 第7题图 第8题图
6.问题:“如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,DF∥AC,求证:△ADE∽△DBF.”某同学的证明过程如下:
证明:①又∵DF∥AC;②∵DE∥BC;③∴△ADE∽△ABC;④∴△DBF∽△ABC;⑤∴△ADE∽△DBF.
步骤正确的顺序是( )
A.③②④①⑤ B.⑤②④①③ C.①③④②⑤ D.②③①④⑤
7.如图,在 ABCD中,点E在AD上,EC交对角线BD于点F,AE∶ED=2∶1,则EF∶FC等于( )
A.1∶1 B.1∶2 C.1∶3 D.2∶3
8.【2021·淄博】如图,AB,CD相交于点E,且AC∥EF∥DB,点C,F,B在同一条直线上,已知AC=p,EF=r,DB=q,则p,q,r之间满足的数量关系式是( )
A.+= B.+= C.+= D.+=
9.【中考·杭州】如图,在△ABC中,点D,E分别在AB和AC边上,DE∥BC,M为BC边上一点(不与点B,C重合),连接AM交DE于点N,则( )
A.= B.= C.= D.=
第9题图 第10题图 第11题图 第12题图
10.【2019·安徽】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G.若EF=EG,则CD的长为( )
A.3.6 B.4 C.4.8 D.5
11.【2020·遂宁】如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G.若AF=2FD,则的值为( )
A. B. C. D.
12.如图,AD是△ABC的中线,点E在AD上,AD=4DE,连接BE并延长,交AC于点F,则AF∶FC的值是( )
A.3∶2 B.4∶3 C.2∶1 D.2∶3
二、填空题
13.如图,在△ABC中,DE∥BC,GF∥AC,GF,DE相交于M点,则图中与△ABC相似的三角形有________个.
第13题图 第14题图 第15题图 第16题图
14.如图,在△ABC中,点D,E分别在AB,AC上,DE∥BC.若AD=4,DB=2,BC=6,则DE的值为________.
15.如图所示是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120 m,DC=60 m,EC=50 m,求得河宽AB= m.
16.【盐城中考】如图,BC∥DE,且BC<DE,AD=BC=4,AB+DE=10.则的值为____.
17.【2020·临沂】如图,在△ABC中,D,E为边AB的三等分点,EF∥DG∥AC,H为AF与DG的交点.若AC=6,则DH=________.
第17题图 第18题图
18.如图,已知在Rt△ABC中,∠C=90°,正方形DCEF的顶点D,E,F分别在边AC,BC,AB上,如果AC=10,BC=6,那么正方形DCEF的周长为________.
三、解答题
19.如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若=,DE=4,求BC的长.
20.如图,DE∥BC,分别交AB,AC于点D,E,连接BE,CD,交于点O.
(1)写出图中的相似三角形;
(2)求证=.
21.已知线段OA⊥OB,点C为OB的中点,点D为AO上一点,连接AC,BD交于点P.
(1)如图①,当点D为AO的中点时,求的值;
(2)如图②,当=时,求的值.
22.【2021·河南省实验学校校级月考】如图,在四边形OABC中,D,E,F分别是OA,OB,OC上的点,连接DE,EF,DF,AC,若∠OED=∠OBA,∠OEF=∠OBC.
(1)求证:=.
(2)请你探究:如果△DEF是以DF为底边的等腰三角形,那么△ABC是否是以AC为底边的等腰三角形,为什么?
23.【2020·泸州改编】如图,在矩形ABCD中,E,F分别为边AB,AD的中点,BF与EC,ED分别交于点M,N.已知AB=4,BC=6,求MN的长.
24.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ.点P,Q分别从点A,C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)直接用含t的式子表示:QB=__________,PD=__________;
(2)是否存在t值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由,并探究如何改变点Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图,AB∥CD∥EF,则图中相似三角形有( B )
A.0对 B.3对 C.2对 D.1对
第1题图 第2题图 第3题图 第4题图
2.【中考·河南】如图,在△ABC中,点D,E分别是AB,AC的中点,则下列结论:①BC=2DE;②△ADE∽△ABC;③=.其中正确的有( A )
A.3个 B.2个 C.1个 D.0个
3.如图,已知BC交AD于点E,AB∥EF∥CD,那么下列结论中不成立的是( C )
A.△DEF∽△DAB B.△BEF∽△BCD C.△BEF∽△DCE D.△ABE∽△DCE
4.【中考·玉林】如图,AB∥EF∥DC,AD∥BC,EF与AC交于点G,则相似三角形共有( C )
A.3对 B.5对 C.6对 D.8对
【点拨】图中三角形有△AEG,△ADC,△CFG,△CBA.由AB∥EF∥DC,AD∥BC,易得△AEG∽△ADC∽△CFG∽△CBA,有6种组合,则相似三角形共有6对.
5.如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( C )
A.= B.= C.= D.=
第5题图 第6题图 第7题图 第8题图
6.问题:“如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,DF∥AC,求证:△ADE∽△DBF.”某同学的证明过程如下:
证明:①又∵DF∥AC;②∵DE∥BC;③∴△ADE∽△ABC;④∴△DBF∽△ABC;⑤∴△ADE∽△DBF.
步骤正确的顺序是( D )
A.③②④①⑤ B.⑤②④①③ C.①③④②⑤ D.②③①④⑤
7.如图,在 ABCD中,点E在AD上,EC交对角线BD于点F,AE∶ED=2∶1,则EF∶FC等于( C )
A.1∶1 B.1∶2 C.1∶3 D.2∶3
8.【2021·淄博】如图,AB,CD相交于点E,且AC∥EF∥DB,点C,F,B在同一条直线上,已知AC=p,EF=r,DB=q,则p,q,r之间满足的数量关系式是( )
A.+= B.+= C.+= D.+=
【点拨】EF∥AC,∴△BEF∽△BAC.∴=.
∵EF∥DB,∴△CEF∽△CDB.∴=.
∴+=+===1,即+=1.
∴+=.
【答案】C
9.【中考·杭州】如图,在△ABC中,点D,E分别在AB和AC边上,DE∥BC,M为BC边上一点(不与点B,C重合),连接AM交DE于点N,则( C )
A.= B.= C.= D.=
第9题图 第10题图 第11题图 第12题图
10.【2019·安徽】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G.若EF=EG,则CD的长为( B )
A.3.6 B.4 C.4.8 D.5
【点拨】如图,作DH∥EG交AB于点H,则△AEG∽△ADH.∴=.
∵EF⊥AC,∠C=90°,∴∠EFA=∠C=90°.
∴EF∥CD.∴△AEF∽△ADC.
∴=∴=.
∵EG=EF,∴DH=CD.
设DH=x,则CD=x.
∵BC=12,AC=6,∴BD=12-x.
∵EF⊥AC,EF⊥EG,DH∥EG,
∴EG∥AC∥DH.∴△BDH∽△BCA.
∴=,即=,解得x=4,∴CD=4.
11.【2020·遂宁】如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G.若AF=2FD,则的值为( )
A. B. C. D.
【点拨】设FD=k,则AF=2k,AD=3k.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD.
∴∠AFB=∠FBC=∠DFG,∠ABF=∠G.
∵BE平分∠ABC,∴∠ABF=∠FBC.
∴∠ABF=∠AFB=∠DFG=∠G.
∴AB=AF=2k,FD=DG=k.
∴CD=2k.
∴CG=CD+DG=3k.
∵AB∥CG,
∴△ABE∽△CGE.
∴===.
【答案】C
12.如图,AD是△ABC的中线,点E在AD上,AD=4DE,连接BE并延长,交AC于点F,则AF∶FC的值是( A )
A.3∶2 B.4∶3 C.2∶1 D.2∶3
【提示】过点D作DG∥AC,与BF交于点G,因此FC=2DG,AF=3DG.
二、填空题
13.如图,在△ABC中,DE∥BC,GF∥AC,GF,DE相交于M点,则图中与△ABC相似的三角形有________个.
【答案】3
第13题图 第14题图 第15题图 第16题图
14.如图,在△ABC中,点D,E分别在AB,AC上,DE∥BC.若AD=4,DB=2,BC=6,则DE的值为________.
【答案】4
15.如图所示是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120 m,DC=60 m,EC=50 m,求得河宽AB= m.
【答案】100
16.【盐城中考】如图,BC∥DE,且BC<DE,AD=BC=4,AB+DE=10.则的值为____.
【答案】2
17.【2020·临沂】如图,在△ABC中,D,E为边AB的三等分点,EF∥DG∥AC,H为AF与DG的交点.若AC=6,则DH=________.
【答案】1
第17题图 第18题图
18.如图,已知在Rt△ABC中,∠C=90°,正方形DCEF的顶点D,E,F分别在边AC,BC,AB上,如果AC=10,BC=6,那么正方形DCEF的周长为________.
【点拨】∵四边形DCEF为正方形,∴DF∥BC,DC=DF,
∴△ADF∽△ACB,∴=,设DC=x,则DF=x,
AD=10-x,∴=,解得x=,
∴正方形DCEF的周长为4×=15.
【答案】15
三、解答题
19.如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若=,DE=4,求BC的长.
解:∵=,∴=.
∵DE∥BC,∴△ADE∽△ABC.
∴==,即=,解得BC=6.
20.如图,DE∥BC,分别交AB,AC于点D,E,连接BE,CD,交于点O.
(1)写出图中的相似三角形;
解:△ADE∽△ABC,△DOE∽△COB.
(2)求证=.
证明:由(1)知△ADE∽△ABC,∴=.
又由(1)知△DOE∽△COB,∴=.
∴=.
21.已知线段OA⊥OB,点C为OB的中点,点D为AO上一点,连接AC,BD交于点P.
(1)如图①,当点D为AO的中点时,求的值;
解:如图①,过点C作CE∥OA,交BD于点E,
∴△BCE∽△BOD.
∴==. ∴CE=OD=AD.
∵CE∥OA,∴△ECP∽△DAP.
∴===2.
(2)如图②,当=时,求的值.
【思路点拨】过一点作平行于三角形一边的线段,构造相似三角形来解决以上两题.12题过AC边的中点E作平行于CD的线段;13题以AP,PC为三角形的对应边,通过作平行线构造相似三角形.
解:如图②,过点C作CE∥OA,交BD于点E,
∴△BCE∽△BOD,∴==.
设AD=x,则OA=4x,OD=3x.∴CE=OD=x.
由OA∥CE得△DAP∽△ECP,
∴===. ∴=.
22.【2021·河南省实验学校校级月考】如图,在四边形OABC中,D,E,F分别是OA,OB,OC上的点,连接DE,EF,DF,AC,若∠OED=∠OBA,∠OEF=∠OBC.
(1)求证:=.
证明:∵∠OED=∠OBA,∠OEF=∠OBC,
∴DE∥AB,EF∥BC.
由DE∥AB,
得△ODE∽△OAB,
∴=.
由EF∥BC,得△OFE∽△OCB,
∴=.∴=.
(2)请你探究:如果△DEF是以DF为底边的等腰三角形,那么△ABC是否是以AC为底边的等腰三角形,为什么?
解:是.理由如下:由△OFE∽△OCB,
得=.
由△ODE∽△OAB,得=.∴=.
∵△DEF是以DF为底边的等腰三角形,
∴DE=EF,
∴AB=BC,即△ABC是以AC为底边的等腰三角形.
23.【2020·泸州改编】如图,在矩形ABCD中,E,F分别为边AB,AD的中点,BF与EC,ED分别交于点M,N.已知AB=4,BC=6,求MN的长.
解:如图,过点E作EH∥AD,交BF于点G,交CD于点H,
∴△BEG∽△BAF,∴=.
∵AB=4,BC=6,E为AB的中点,F为AD的中点,
∴BE=2,AF=DF=3,∴=,∴EG=.
由题意易得△EGN∽△DFN,△EGM∽△CBM,
∴=,=,
∴=,=,即=,=,
∴2NG=NF,4MG=MB.
∵E为AB的中点,EH∥AD,∴G为BF的中点,
∴BG=GF=BF= =,
∴NG=GF=,MG=BG=,
∴MN=NG+MG=.
24.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ.点P,Q分别从点A,C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)直接用含t的式子表示:QB=__________,PD=__________;
【答案】8-2t t
(2)是否存在t值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由,并探究如何改变点Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形.
解:不存在.理由如下:
在Rt△ABC中,∠C=90°,AC=6,BC=8,
∴AB=10.
∵PD∥BC,∴△APD∽△ACB,
∴=,即=,∴AD=t.
∴BD=AB-AD=10-t.
∵BQ∥DP,
∴当BQ=DP时,四边形PDBQ是平行四边形,
即8-2t=t,解得t=.
当t=时,PD=×=,BD=10-×=6,
∴DP≠BD,∴四边形PDBQ不能为菱形.
设点Q的速度为每秒v个单位长度时满足条件,则BQ=8-vt,PD=t,BD=10-t.要使四边形PDBQ为菱形,则PD=BD=BQ.
∴t=10-t=8-vt,解得t=,v=.
∴当点Q的速度为每秒个单位长度时,经过秒,四边形PDBQ为菱形.
