27.2.3 相似三角形应用举例 同步练习(含答案)
文档属性
| 名称 | 27.2.3 相似三角形应用举例 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 16:46:00 | ||
图片预览



文档简介
27.2 相似三角形
27.2.3 相似三角形应用举例
一、选择题
1.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高为1.5 m,测得AB=3 m,BC=7 m,则建筑物CD的高是( )
A.3.5 m B.4 m C.4.5 m D.5 m
第1题图 第2题图 第3题图 第5题图
2.为了估计河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得AB⊥BC,设BC与AE交于点D,如图所示测得BD=120 m,DC=40 m,EC=30 m,那么这条河的大致宽度是( )
A.90 m B.60 m C.100 m D.120 m
3.如图,在圆形花圃中有两条笔直的小径,两端都在花圃边界上,分别记为AC,BD,设交点为P,点C,D之间有一座假山,为了测量C,D之间的距离,小明已经测量了线段AP和PD的长度,只需再测量一条线段的长度,就可以计算C,D之间的距离.小明应该测量的是( )
A.线段BP B.线段CP C.线段AB D.线段AD
4.有一个三角形木架的三边长分别是15 cm,20 cm,24 cm,现要再做一个与其相似的三角形木架,而只有长为12 cm和24 cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( )
A.一种 B.两种 C.三种 D.四种
5.如图,阳光通过窗口照到室内,在地上留下3 m宽的亮区,已知亮区一边到窗下墙角的距离CE=7 m,窗口的高AB=1.8 m,那么窗口底边离地面的高BC等于( )
A.2 m B.2.4 m C.2.8 m D.3 m
6.【2021甘肃兰州期末】如图是小明设计的用手电筒来测量某古城墙高度的示意图.在地面上点P处放一水平的平面镜,光从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=18米,那么该古城墙的高度是( )
A.6 米 B.8 米 C.12 米 D.24 米
第6题图 第7题图 第9题图
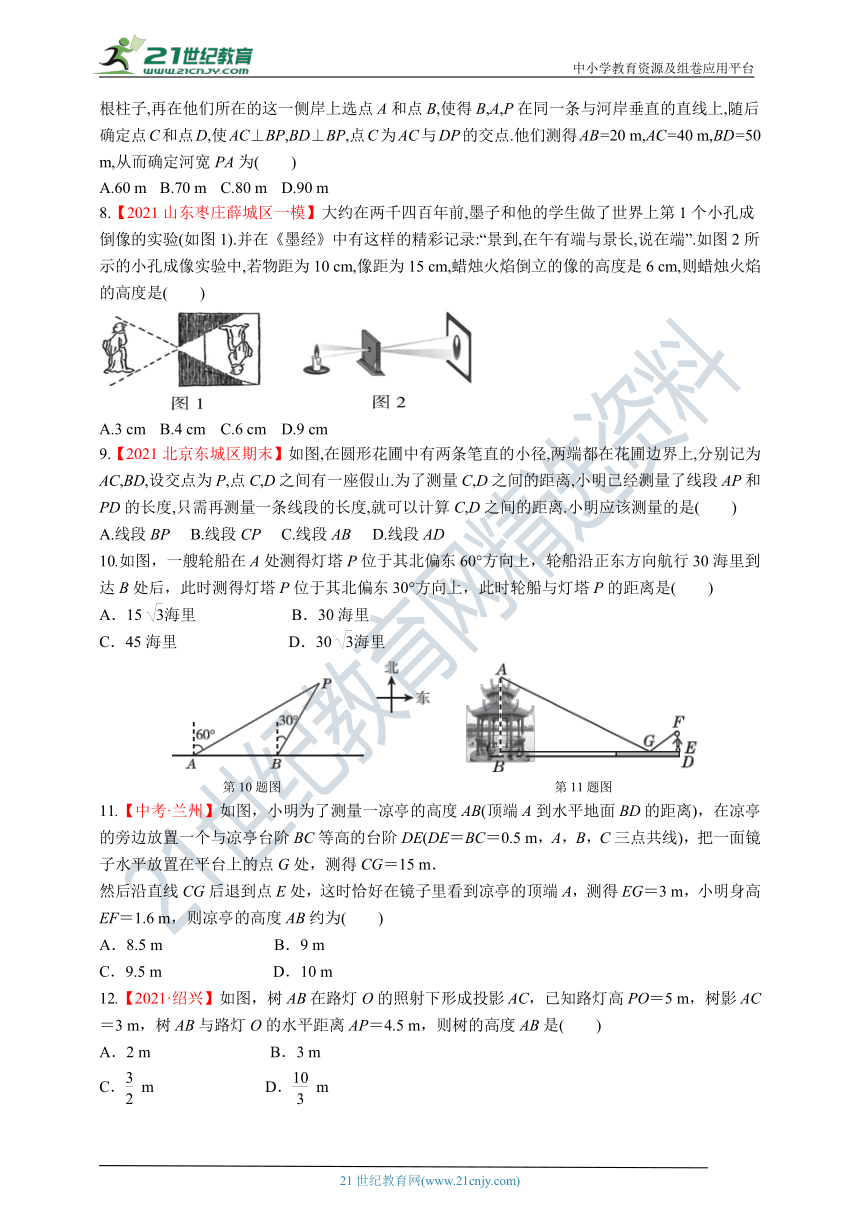
7.【2021河南郑州期末】如图,为了确定一条河的宽度,测量人员先观察到在对岸岸边P点处有一根柱子,再在他们所在的这一侧岸上选点A和点B,使得B,A,P在同一条与河岸垂直的直线上,随后确定点C和点D,使AC⊥BP,BD⊥BP,点C为AC与DP的交点.他们测得AB=20 m,AC=40 m,BD=50 m,从而确定河宽PA为( )
A.60 m B.70 m C.80 m D.90 m
8.【2021山东枣庄薛城区一模】大约在两千四百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验(如图1).并在《墨经》中有这样的精彩记录:“景到,在午有端与景长,说在端”.如图2所示的小孔成像实验中,若物距为10 cm,像距为15 cm,蜡烛火焰倒立的像的高度是6 cm,则蜡烛火焰的高度是( )
A.3 cm B.4 cm C.6 cm D.9 cm
9.【2021北京东城区期末】如图,在圆形花圃中有两条笔直的小径,两端都在花圃边界上,分别记为AC,BD,设交点为P,点C,D之间有一座假山.为了测量C,D之间的距离,小明已经测量了线段AP和PD的长度,只需再测量一条线段的长度,就可以计算C,D之间的距离.小明应该测量的是( )
A.线段BP B.线段CP C.线段AB D.线段AD
10.如图,一艘轮船在A处测得灯塔P位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是( )
A.15海里 B.30海里
C.45海里 D.30海里
第10题图 第11题图
11.【中考·兰州】如图,小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE=BC=0.5 m,A,B,C三点共线),把一面镜子水平放置在平台上的点G处,测得CG=15 m.
然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得EG=3 m,小明身高EF=1.6 m,则凉亭的高度AB约为( )
A.8.5 m B.9 m
C.9.5 m D.10 m
12.【2021·绍兴】如图,树AB在路灯O的照射下形成投影AC,已知路灯高PO=5 m,树影AC=3 m,树AB与路灯O的水平距离AP=4.5 m,则树的高度AB是( )
A.2 m B.3 m
C. m D. m
第12题图 第13题图
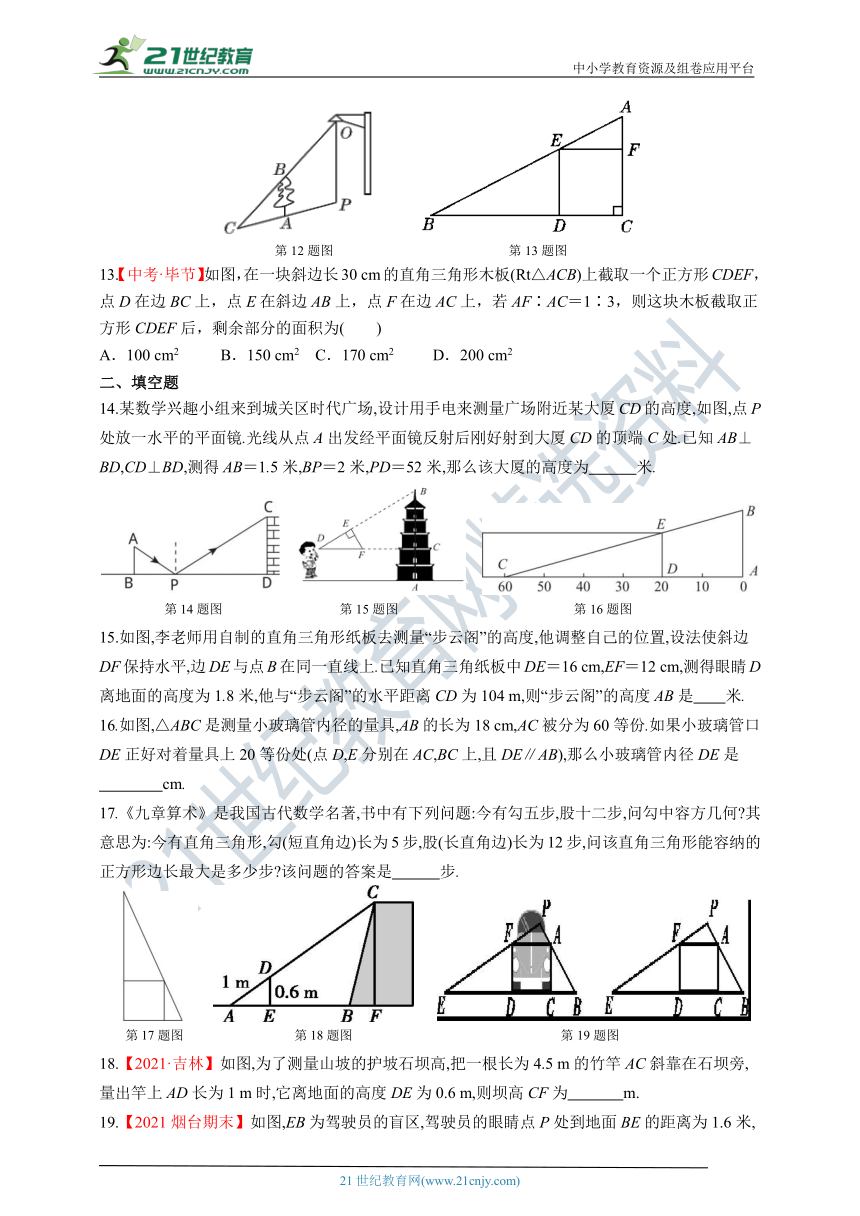
13.【中考·毕节】如图,在一块斜边长30 cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF∶AC=1∶3,则这块木板截取正方形CDEF后,剩余部分的面积为( )
A.100 cm2 B.150 cm2 C.170 cm2 D.200 cm2
二、填空题
14.某数学兴趣小组来到城关区时代广场,设计用手电来测量广场附近某大厦CD的高度,如图,点P处放一水平的平面镜.光线从点A出发经平面镜反射后刚好射到大厦CD的顶端C处.已知AB⊥BD,CD⊥BD,测得AB=1.5米,BP=2米,PD=52米,那么该大厦的高度为 米.
第14题图 第15题图 第16题图
15.如图,李老师用自制的直角三角形纸板去测量“步云阁”的高度,他调整自己的位置,设法使斜边DF保持水平,边DE与点B在同一直线上.已知直角三角纸板中DE=16 cm,EF=12 cm,测得眼睛D离地面的高度为1.8米,他与“步云阁”的水平距离CD为104 m,则“步云阁”的高度AB是 米.
16.如图,△ABC是测量小玻璃管内径的量具,AB的长为18 cm,AC被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(点D,E分别在AC,BC上,且DE∥AB),那么小玻璃管内径DE是
cm.
17.《九章算术》是我国古代数学名著,书中有下列问题:今有勾五步,股十二步,问勾中容方几何 其意思为:今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步 该问题的答案是 步.
第17题图 第18题图 第19题图
18.【2021·吉林】如图,为了测量山坡的护坡石坝高,把一根长为4.5 m的竹竿AC斜靠在石坝旁,量出竿上AD长为1 m时,它离地面的高度DE为0.6 m,则坝高CF为 m.
19.【2021烟台期末】如图,EB为驾驶员的盲区,驾驶员的眼睛点P处到地面BE的距离为1.6米,车头FACD近似看成一个矩形,且满足3FD=2FA,若盲区EB的长度是6米,则车宽FA为 米.
三、解答题
20.《孙子算经》中有道歌谣算题:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸.问竿长几何 其意思为:有一根竹竿不知道有多长,量出它在太阳下的影长为一丈五尺.同时立一根一尺五寸的小标杆,它的影长为五寸.请你算一算竹竿的长度是多少.(其中丈和尺是古代的长度单位,1丈=10尺,1尺=10寸)
21.如图,建筑物BC上有一个旗杆AB,小芳计划用学过的知识测量该建筑物的高度,测量方法如下:在该建筑物底部所在的平地上有一棵小树FD,小芳沿CD后退,发现地面上的点E、树顶F、旗杆顶端A恰好在一条直线上,继续后退,发现地面上的点G、树顶F、建筑物顶端B恰好在一条直线上.已知旗杆AB=3米,FD=4米,DE=5米,EG=1.5米,点A,B,C在一条直线上,点C,D,E,G在一条直线上,AC,FD均垂直于CG,请你帮助小芳求出这座建筑物的高BC.
22.如图,李明用自制的直角三角形纸板去测量“步云阁”的高度,他调整自己的位置,设法使斜边DF保持水平,边DE与点B在同一直线上,已知直角三角形纸板中DE=16 cm,EF=12 cm,测得眼睛D离地面的高度为1.8 m,他与“步云阁”的水平距离CD为104 m,求“步云阁”的高度AB.
23.如图,小华和同伴春游时,发现在某地小山坡的点E处有一棵小桃树,他们想利用皮尺、测角仪和平面镜测量小桃树到山脚下的距离(即DE的长度),小华站在点B处,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E,且测得BC=6米,CD=24米,∠CDE=135°.已知小华的眼睛距地面的高度AB=1.5米,请根据以上数据,求DE的长度.(结果保留根号)
24.青龙寺是西安最著名的樱花观赏地,樱花品种达到了13种之多,每年3,4月陆续开放的樱花让这里成了花的海洋.一天,小明和小刚去青龙寺游玩,想利用所学知识测量一棵樱花树的高度(樱花树四周被围起来了,底部不易到达).小明在F处竖立了一根标杆EF,小刚走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上.此时测得小刚的眼睛到地面的距离DC=1.6米;然后,小刚在C处蹲下,小明平移标杆到H处时,小刚恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小刚的眼睛到地面的距离MC=0.8米.已知EF=GH=2.4米,CF=2米,FH=1.6米,点C,F,H,A在一条直线上,点M在CD上,CD⊥AC,EF⊥AC,GH⊥AC,AB⊥AC.根据以上测量过程及测量数据,请你求出这棵樱花树AB的高度.
25.小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)如图1,垂直于地面放置的正方形框架ABCD,边长AB为30 cm,在其正上方有一个灯泡,在灯泡的照射下,正方形框架的横向影子A'B,D'C的长度和为6 cm,那么灯泡离地面的高度为 .
(2)不改变图1中灯泡的高度,将两个边长为30 cm的正方形框架按图2摆放,灯泡仍处于两个正方形的正上方.请计算此时横向影子A'B,D'C的长度和为多少
(3)有n个边长为a的正方形按图3摆放,测得横向影子A'B,D'C的长度和为b,灯泡处于n个正方形的正上方.求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高为1.5 m,测得AB=3 m,BC=7 m,则建筑物CD的高是( D )
A.3.5 m B.4 m C.4.5 m D.5 m
第1题图 第2题图 第3题图 第5题图
2.为了估计河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得AB⊥BC,设BC与AE交于点D,如图所示测得BD=120 m,DC=40 m,EC=30 m,那么这条河的大致宽度是( A )
A.90 m B.60 m C.100 m D.120 m
3.如图,在圆形花圃中有两条笔直的小径,两端都在花圃边界上,分别记为AC,BD,设交点为P,点C,D之间有一座假山,为了测量C,D之间的距离,小明已经测量了线段AP和PD的长度,只需再测量一条线段的长度,就可以计算C,D之间的距离.小明应该测量的是( C )
A.线段BP B.线段CP C.线段AB D.线段AD
4.有一个三角形木架的三边长分别是15 cm,20 cm,24 cm,现要再做一个与其相似的三角形木架,而只有长为12 cm和24 cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( B )
A.一种 B.两种 C.三种 D.四种
5.如图,阳光通过窗口照到室内,在地上留下3 m宽的亮区,已知亮区一边到窗下墙角的距离CE=7 m,窗口的高AB=1.8 m,那么窗口底边离地面的高BC等于( B )
A.2 m B.2.4 m C.2.8 m D.3 m
6.【2021甘肃兰州期末】如图是小明设计的用手电筒来测量某古城墙高度的示意图.在地面上点P处放一水平的平面镜,光从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=18米,那么该古城墙的高度是( )
A.6 米 B.8 米 C.12 米 D.24 米
第6题图 第7题图 第9题图
【答案】C
【解析】由题意,知∠APB=∠CPD,∠ABP=∠CDP,∴Rt△ABP∽Rt△CDP,∴=,∵AB=1.2米,
BP=1.8米,PD=18米,∴=,∴CD=12米.
7.【2021河南郑州期末】如图,为了确定一条河的宽度,测量人员先观察到在对岸岸边P点处有一根柱子,再在他们所在的这一侧岸上选点A和点B,使得B,A,P在同一条与河岸垂直的直线上,随后确定点C和点D,使AC⊥BP,BD⊥BP,点C为AC与DP的交点.他们测得AB=20 m,AC=40 m,BD=50 m,从而确定河宽PA为( )
A.60 m B.70 m C.80 m D.90 m
【答案】C
【解析】∵AC⊥BP,BD⊥BP,∴AC∥BD,∴△PBD∽△PAC,∴=.∵AB=20 m,AC=40m,BD=50 m,
∴=,∴PA=80 m.
8.【2021山东枣庄薛城区一模】大约在两千四百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验(如图1).并在《墨经》中有这样的精彩记录:“景到,在午有端与景长,说在端”.如图2所示的小孔成像实验中,若物距为10 cm,像距为15 cm,蜡烛火焰倒立的像的高度是6 cm,则蜡烛火焰的高度是( )
A.3 cm B.4 cm C.6 cm D.9 cm
【答案】B
【解析】设蜡烛火焰的高度是x cm,由相似三角形的性质,得=,解得x=4,故蜡烛火焰的高度是4 cm.
9.【2021北京东城区期末】如图,在圆形花圃中有两条笔直的小径,两端都在花圃边界上,分别记为AC,BD,设交点为P,点C,D之间有一座假山.为了测量C,D之间的距离,小明已经测量了线段AP和PD的长度,只需再测量一条线段的长度,就可以计算C,D之间的距离.小明应该测量的是( )
A.线段BP B.线段CP C.线段AB D.线段AD
【答案】C
【解析】如图,连接AB,∵∠A=∠D,∠B=∠C,∴△APB∽△DPC,∴=,∴需要测量线段AB的长度.
10.如图,一艘轮船在A处测得灯塔P位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是( B )
A.15海里 B.30海里 C.45海里 D.30海里
第10题图 第11题图
11.【中考·兰州】如图,小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE=BC=0.5 m,A,B,C三点共线),把一面镜子水平放置在平台上的点G处,测得CG=15 m.
然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得EG=3 m,小明身高EF=1.6 m,则凉亭的高度AB约为( A )
A.8.5 m B.9 m C.9.5 m D.10 m
【点拨】由题意知∠AGC=∠FGE.
∵∠ACG=∠FEG=90°,
∴△ACG∽△FEG.
∴=.∴=.∴AC=8 m.
∴AB=AC+BC=8+0.5=8.5(m).
12.【2021·绍兴】如图,树AB在路灯O的照射下形成投影AC,已知路灯高PO=5 m,树影AC=3 m,树AB与路灯O的水平距离AP=4.5 m,则树的高度AB是( A )
A.2 m B.3 m C. m D. m
第12题图 第13题图
13.【中考·毕节】如图,在一块斜边长30 cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF∶AC=1∶3,则这块木板截取正方形CDEF后,剩余部分的面积为( )
A.100 cm2 B.150 cm2 C.170 cm2 D.200 cm2
【点拨】设AF=x cm,则AC=3x cm.
∵四边形CDEF为正方形,∴EF=CF=2x cm,EF∥BC,
∴△AEF∽△ABC,∴==,∴BC=6x cm.
在Rt△ABC中,AB2=AC2+BC2,即302=(3x)2+(6x)2,
解得x=2(负值已舍去),
∴CF=4 cm,AC=6 cm,BC=12 cm,
∴剩余部分的面积=×12×6-4×4=100(cm2).
【答案】A
二、填空题
14.某数学兴趣小组来到城关区时代广场,设计用手电来测量广场附近某大厦CD的高度,如图,点P处放一水平的平面镜.光线从点A出发经平面镜反射后刚好射到大厦CD的顶端C处.已知AB⊥BD,CD⊥BD,测得AB=1.5米,BP=2米,PD=52米,那么该大厦的高度为 39 米.
第14题图 第15题图 第16题图
15.如图,李老师用自制的直角三角形纸板去测量“步云阁”的高度,他调整自己的位置,设法使斜边DF保持水平,边DE与点B在同一直线上.已知直角三角纸板中DE=16 cm,EF=12 cm,测得眼睛D离地面的高度为1.8米,他与“步云阁”的水平距离CD为104 m,则“步云阁”的高度AB是 79.8 米.
16.如图,△ABC是测量小玻璃管内径的量具,AB的长为18 cm,AC被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(点D,E分别在AC,BC上,且DE∥AB),那么小玻璃管内径DE是 12 cm.
17.《九章算术》是我国古代数学名著,书中有下列问题:今有勾五步,股十二步,问勾中容方几何 其意思为:今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步 该问题的答案是 步.
第17题图 第18题图 第19题图
18.【2021·吉林】如图,为了测量山坡的护坡石坝高,把一根长为4.5 m的竹竿AC斜靠在石坝旁,量出竿上AD长为1 m时,它离地面的高度DE为0.6 m,则坝高CF为 m.
【答案】2.7
【解析】由题意,得DE∥CF,∴△ADE∽△ACF,∴=,即=,∴CF=2.7 m.
19.【2021烟台期末】如图,EB为驾驶员的盲区,驾驶员的眼睛点P处到地面BE的距离为1.6米,车头FACD近似看成一个矩形,且满足3FD=2FA,若盲区EB的长度是6米,则车宽FA为 米.
【答案】
【解析】如图,过点P作PM⊥BE,垂足为M,交AF于点N,则PM=1.6米,设FA=x米,由3FD=2FA,得FD=x=MN.∵四边形ACDF是矩形,∴AF∥CD,∴△PAF∽△PBE,∴=,即=,∴PN=x.∵PN+MN=PM,∴x+x=1.6,解得x=,故FA= 米.
三、解答题
20.《孙子算经》中有道歌谣算题:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸.问竿长几何 其意思为:有一根竹竿不知道有多长,量出它在太阳下的影长为一丈五尺.同时立一根一尺五寸的小标杆,它的影长为五寸.请你算一算竹竿的长度是多少.(其中丈和尺是古代的长度单位,1丈=10尺,1尺=10寸)
解:设竹竿的长度为x尺.
依题意,得,解得x=45.
答:竹竿的长度是45尺.
21.如图,建筑物BC上有一个旗杆AB,小芳计划用学过的知识测量该建筑物的高度,测量方法如下:在该建筑物底部所在的平地上有一棵小树FD,小芳沿CD后退,发现地面上的点E、树顶F、旗杆顶端A恰好在一条直线上,继续后退,发现地面上的点G、树顶F、建筑物顶端B恰好在一条直线上.已知旗杆AB=3米,FD=4米,DE=5米,EG=1.5米,点A,B,C在一条直线上,点C,D,E,G在一条直线上,AC,FD均垂直于CG,请你帮助小芳求出这座建筑物的高BC.
解:由题知∠ACE=∠FDE=90°,∠AEC=∠FED,
∴△ACE∽△FDE,∴. ①
又∵∠BCG=∠FDG=90°,∠BGC=∠FGD,
∴△BCG∽△FDG,∴. ②
联立①②,得BC=14.
答:这座建筑物的高BC为14米.
22.如图,李明用自制的直角三角形纸板去测量“步云阁”的高度,他调整自己的位置,设法使斜边DF保持水平,边DE与点B在同一直线上,已知直角三角形纸板中DE=16 cm,EF=12 cm,测得眼睛D离地面的高度为1.8 m,他与“步云阁”的水平距离CD为104 m,求“步云阁”的高度AB.
【解析】 在△DEF和△DCB中,∠D=∠D,∠DEF=∠DCB=90°,
∴△DEF∽△DCB,∴=,即=,∴BC=78 m.
∵AC=1.8 m,∴AB=AC+BC=79.8 m.
答:“步云阁”的高度AB为79.8 m.
23.如图,小华和同伴春游时,发现在某地小山坡的点E处有一棵小桃树,他们想利用皮尺、测角仪和平面镜测量小桃树到山脚下的距离(即DE的长度),小华站在点B处,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E,且测得BC=6米,CD=24米,∠CDE=135°.已知小华的眼睛距地面的高度AB=1.5米,请根据以上数据,求DE的长度.(结果保留根号)
【解析】 如图,过点E作EF⊥BC于点F,
∵∠CDE=135°,∴∠EDF=45°,∴DF=EF.
设EF=x米,则DF=x米,DE=x米,
∵∠B=∠EFC=90°,∠ACB=∠ECD,
∴△ABC∽△EFC,∴=,
即=,∴x=8,∴DE=8 米,
故DE的长度为8 米.
24.青龙寺是西安最著名的樱花观赏地,樱花品种达到了13种之多,每年3,4月陆续开放的樱花让这里成了花的海洋.一天,小明和小刚去青龙寺游玩,想利用所学知识测量一棵樱花树的高度(樱花树四周被围起来了,底部不易到达).小明在F处竖立了一根标杆EF,小刚走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上.此时测得小刚的眼睛到地面的距离DC=1.6米;然后,小刚在C处蹲下,小明平移标杆到H处时,小刚恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小刚的眼睛到地面的距离MC=0.8米.已知EF=GH=2.4米,CF=2米,FH=1.6米,点C,F,H,A在一条直线上,点M在CD上,CD⊥AC,EF⊥AC,GH⊥AC,AB⊥AC.根据以上测量过程及测量数据,请你求出这棵樱花树AB的高度.
【解析】 如图,过点D作DP⊥AB于点P,交EF于点N,过点M作MQ⊥AB于点Q,交GH于点K,
由题意,得DP=MQ=AC,DN=CF=2米,MK=CH,AP=DC=1.6米,AQ=HK=MC=0.8米.
∵∠EDN=∠BDP,∠END=∠BPD=90°,∠GMK=∠BMQ,∠GKM=∠BQM=90°,∴△DEN∽△DBP,△GMK∽△BMQ,
∴=,=,∴=,=,
∴AB=8.8米.
答:这棵樱花树AB的高度是8.8米.
25.小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)如图1,垂直于地面放置的正方形框架ABCD,边长AB为30 cm,在其正上方有一个灯泡,在灯泡的照射下,正方形框架的横向影子A'B,D'C的长度和为6 cm,那么灯泡离地面的高度为180cm.
(2)不改变图1中灯泡的高度,将两个边长为30 cm的正方形框架按图2摆放,灯泡仍处于两个正方形的正上方.请计算此时横向影子A'B,D'C的长度和为多少
(3)有n个边长为a的正方形按图3摆放,测得横向影子A'B,D'C的长度和为b,灯泡处于n个正方形的正上方.求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
解:(2)设横向影子A'B,D'C的长度和为y cm,灯泡的位置为点P.
∵AD∥A'D',∴∠PAD=∠PA'D',∠PDA=∠PD'A',
∴△PAD∽△PA'D'.
根据相似三角形对应高的比等于相似比的性质,可得,
∴,解得y=12.
∴此时横向影子A'B,D'C的长度和为12 cm.
(3)设灯泡离地面的距离为x,记灯泡为点P.
由题意得PM=x,PN=x-a,AD=na,A'D'=na+b,同理可得,
∴灯泡离地面的距离为.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
27.2.3 相似三角形应用举例
一、选择题
1.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高为1.5 m,测得AB=3 m,BC=7 m,则建筑物CD的高是( )
A.3.5 m B.4 m C.4.5 m D.5 m
第1题图 第2题图 第3题图 第5题图
2.为了估计河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得AB⊥BC,设BC与AE交于点D,如图所示测得BD=120 m,DC=40 m,EC=30 m,那么这条河的大致宽度是( )
A.90 m B.60 m C.100 m D.120 m
3.如图,在圆形花圃中有两条笔直的小径,两端都在花圃边界上,分别记为AC,BD,设交点为P,点C,D之间有一座假山,为了测量C,D之间的距离,小明已经测量了线段AP和PD的长度,只需再测量一条线段的长度,就可以计算C,D之间的距离.小明应该测量的是( )
A.线段BP B.线段CP C.线段AB D.线段AD
4.有一个三角形木架的三边长分别是15 cm,20 cm,24 cm,现要再做一个与其相似的三角形木架,而只有长为12 cm和24 cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( )
A.一种 B.两种 C.三种 D.四种
5.如图,阳光通过窗口照到室内,在地上留下3 m宽的亮区,已知亮区一边到窗下墙角的距离CE=7 m,窗口的高AB=1.8 m,那么窗口底边离地面的高BC等于( )
A.2 m B.2.4 m C.2.8 m D.3 m
6.【2021甘肃兰州期末】如图是小明设计的用手电筒来测量某古城墙高度的示意图.在地面上点P处放一水平的平面镜,光从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=18米,那么该古城墙的高度是( )
A.6 米 B.8 米 C.12 米 D.24 米
第6题图 第7题图 第9题图
7.【2021河南郑州期末】如图,为了确定一条河的宽度,测量人员先观察到在对岸岸边P点处有一根柱子,再在他们所在的这一侧岸上选点A和点B,使得B,A,P在同一条与河岸垂直的直线上,随后确定点C和点D,使AC⊥BP,BD⊥BP,点C为AC与DP的交点.他们测得AB=20 m,AC=40 m,BD=50 m,从而确定河宽PA为( )
A.60 m B.70 m C.80 m D.90 m
8.【2021山东枣庄薛城区一模】大约在两千四百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验(如图1).并在《墨经》中有这样的精彩记录:“景到,在午有端与景长,说在端”.如图2所示的小孔成像实验中,若物距为10 cm,像距为15 cm,蜡烛火焰倒立的像的高度是6 cm,则蜡烛火焰的高度是( )
A.3 cm B.4 cm C.6 cm D.9 cm
9.【2021北京东城区期末】如图,在圆形花圃中有两条笔直的小径,两端都在花圃边界上,分别记为AC,BD,设交点为P,点C,D之间有一座假山.为了测量C,D之间的距离,小明已经测量了线段AP和PD的长度,只需再测量一条线段的长度,就可以计算C,D之间的距离.小明应该测量的是( )
A.线段BP B.线段CP C.线段AB D.线段AD
10.如图,一艘轮船在A处测得灯塔P位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是( )
A.15海里 B.30海里
C.45海里 D.30海里
第10题图 第11题图
11.【中考·兰州】如图,小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE=BC=0.5 m,A,B,C三点共线),把一面镜子水平放置在平台上的点G处,测得CG=15 m.
然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得EG=3 m,小明身高EF=1.6 m,则凉亭的高度AB约为( )
A.8.5 m B.9 m
C.9.5 m D.10 m
12.【2021·绍兴】如图,树AB在路灯O的照射下形成投影AC,已知路灯高PO=5 m,树影AC=3 m,树AB与路灯O的水平距离AP=4.5 m,则树的高度AB是( )
A.2 m B.3 m
C. m D. m
第12题图 第13题图
13.【中考·毕节】如图,在一块斜边长30 cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF∶AC=1∶3,则这块木板截取正方形CDEF后,剩余部分的面积为( )
A.100 cm2 B.150 cm2 C.170 cm2 D.200 cm2
二、填空题
14.某数学兴趣小组来到城关区时代广场,设计用手电来测量广场附近某大厦CD的高度,如图,点P处放一水平的平面镜.光线从点A出发经平面镜反射后刚好射到大厦CD的顶端C处.已知AB⊥BD,CD⊥BD,测得AB=1.5米,BP=2米,PD=52米,那么该大厦的高度为 米.
第14题图 第15题图 第16题图
15.如图,李老师用自制的直角三角形纸板去测量“步云阁”的高度,他调整自己的位置,设法使斜边DF保持水平,边DE与点B在同一直线上.已知直角三角纸板中DE=16 cm,EF=12 cm,测得眼睛D离地面的高度为1.8米,他与“步云阁”的水平距离CD为104 m,则“步云阁”的高度AB是 米.
16.如图,△ABC是测量小玻璃管内径的量具,AB的长为18 cm,AC被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(点D,E分别在AC,BC上,且DE∥AB),那么小玻璃管内径DE是
cm.
17.《九章算术》是我国古代数学名著,书中有下列问题:今有勾五步,股十二步,问勾中容方几何 其意思为:今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步 该问题的答案是 步.
第17题图 第18题图 第19题图
18.【2021·吉林】如图,为了测量山坡的护坡石坝高,把一根长为4.5 m的竹竿AC斜靠在石坝旁,量出竿上AD长为1 m时,它离地面的高度DE为0.6 m,则坝高CF为 m.
19.【2021烟台期末】如图,EB为驾驶员的盲区,驾驶员的眼睛点P处到地面BE的距离为1.6米,车头FACD近似看成一个矩形,且满足3FD=2FA,若盲区EB的长度是6米,则车宽FA为 米.
三、解答题
20.《孙子算经》中有道歌谣算题:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸.问竿长几何 其意思为:有一根竹竿不知道有多长,量出它在太阳下的影长为一丈五尺.同时立一根一尺五寸的小标杆,它的影长为五寸.请你算一算竹竿的长度是多少.(其中丈和尺是古代的长度单位,1丈=10尺,1尺=10寸)
21.如图,建筑物BC上有一个旗杆AB,小芳计划用学过的知识测量该建筑物的高度,测量方法如下:在该建筑物底部所在的平地上有一棵小树FD,小芳沿CD后退,发现地面上的点E、树顶F、旗杆顶端A恰好在一条直线上,继续后退,发现地面上的点G、树顶F、建筑物顶端B恰好在一条直线上.已知旗杆AB=3米,FD=4米,DE=5米,EG=1.5米,点A,B,C在一条直线上,点C,D,E,G在一条直线上,AC,FD均垂直于CG,请你帮助小芳求出这座建筑物的高BC.
22.如图,李明用自制的直角三角形纸板去测量“步云阁”的高度,他调整自己的位置,设法使斜边DF保持水平,边DE与点B在同一直线上,已知直角三角形纸板中DE=16 cm,EF=12 cm,测得眼睛D离地面的高度为1.8 m,他与“步云阁”的水平距离CD为104 m,求“步云阁”的高度AB.
23.如图,小华和同伴春游时,发现在某地小山坡的点E处有一棵小桃树,他们想利用皮尺、测角仪和平面镜测量小桃树到山脚下的距离(即DE的长度),小华站在点B处,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E,且测得BC=6米,CD=24米,∠CDE=135°.已知小华的眼睛距地面的高度AB=1.5米,请根据以上数据,求DE的长度.(结果保留根号)
24.青龙寺是西安最著名的樱花观赏地,樱花品种达到了13种之多,每年3,4月陆续开放的樱花让这里成了花的海洋.一天,小明和小刚去青龙寺游玩,想利用所学知识测量一棵樱花树的高度(樱花树四周被围起来了,底部不易到达).小明在F处竖立了一根标杆EF,小刚走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上.此时测得小刚的眼睛到地面的距离DC=1.6米;然后,小刚在C处蹲下,小明平移标杆到H处时,小刚恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小刚的眼睛到地面的距离MC=0.8米.已知EF=GH=2.4米,CF=2米,FH=1.6米,点C,F,H,A在一条直线上,点M在CD上,CD⊥AC,EF⊥AC,GH⊥AC,AB⊥AC.根据以上测量过程及测量数据,请你求出这棵樱花树AB的高度.
25.小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)如图1,垂直于地面放置的正方形框架ABCD,边长AB为30 cm,在其正上方有一个灯泡,在灯泡的照射下,正方形框架的横向影子A'B,D'C的长度和为6 cm,那么灯泡离地面的高度为 .
(2)不改变图1中灯泡的高度,将两个边长为30 cm的正方形框架按图2摆放,灯泡仍处于两个正方形的正上方.请计算此时横向影子A'B,D'C的长度和为多少
(3)有n个边长为a的正方形按图3摆放,测得横向影子A'B,D'C的长度和为b,灯泡处于n个正方形的正上方.求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高为1.5 m,测得AB=3 m,BC=7 m,则建筑物CD的高是( D )
A.3.5 m B.4 m C.4.5 m D.5 m
第1题图 第2题图 第3题图 第5题图
2.为了估计河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得AB⊥BC,设BC与AE交于点D,如图所示测得BD=120 m,DC=40 m,EC=30 m,那么这条河的大致宽度是( A )
A.90 m B.60 m C.100 m D.120 m
3.如图,在圆形花圃中有两条笔直的小径,两端都在花圃边界上,分别记为AC,BD,设交点为P,点C,D之间有一座假山,为了测量C,D之间的距离,小明已经测量了线段AP和PD的长度,只需再测量一条线段的长度,就可以计算C,D之间的距离.小明应该测量的是( C )
A.线段BP B.线段CP C.线段AB D.线段AD
4.有一个三角形木架的三边长分别是15 cm,20 cm,24 cm,现要再做一个与其相似的三角形木架,而只有长为12 cm和24 cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( B )
A.一种 B.两种 C.三种 D.四种
5.如图,阳光通过窗口照到室内,在地上留下3 m宽的亮区,已知亮区一边到窗下墙角的距离CE=7 m,窗口的高AB=1.8 m,那么窗口底边离地面的高BC等于( B )
A.2 m B.2.4 m C.2.8 m D.3 m
6.【2021甘肃兰州期末】如图是小明设计的用手电筒来测量某古城墙高度的示意图.在地面上点P处放一水平的平面镜,光从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=18米,那么该古城墙的高度是( )
A.6 米 B.8 米 C.12 米 D.24 米
第6题图 第7题图 第9题图
【答案】C
【解析】由题意,知∠APB=∠CPD,∠ABP=∠CDP,∴Rt△ABP∽Rt△CDP,∴=,∵AB=1.2米,
BP=1.8米,PD=18米,∴=,∴CD=12米.
7.【2021河南郑州期末】如图,为了确定一条河的宽度,测量人员先观察到在对岸岸边P点处有一根柱子,再在他们所在的这一侧岸上选点A和点B,使得B,A,P在同一条与河岸垂直的直线上,随后确定点C和点D,使AC⊥BP,BD⊥BP,点C为AC与DP的交点.他们测得AB=20 m,AC=40 m,BD=50 m,从而确定河宽PA为( )
A.60 m B.70 m C.80 m D.90 m
【答案】C
【解析】∵AC⊥BP,BD⊥BP,∴AC∥BD,∴△PBD∽△PAC,∴=.∵AB=20 m,AC=40m,BD=50 m,
∴=,∴PA=80 m.
8.【2021山东枣庄薛城区一模】大约在两千四百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验(如图1).并在《墨经》中有这样的精彩记录:“景到,在午有端与景长,说在端”.如图2所示的小孔成像实验中,若物距为10 cm,像距为15 cm,蜡烛火焰倒立的像的高度是6 cm,则蜡烛火焰的高度是( )
A.3 cm B.4 cm C.6 cm D.9 cm
【答案】B
【解析】设蜡烛火焰的高度是x cm,由相似三角形的性质,得=,解得x=4,故蜡烛火焰的高度是4 cm.
9.【2021北京东城区期末】如图,在圆形花圃中有两条笔直的小径,两端都在花圃边界上,分别记为AC,BD,设交点为P,点C,D之间有一座假山.为了测量C,D之间的距离,小明已经测量了线段AP和PD的长度,只需再测量一条线段的长度,就可以计算C,D之间的距离.小明应该测量的是( )
A.线段BP B.线段CP C.线段AB D.线段AD
【答案】C
【解析】如图,连接AB,∵∠A=∠D,∠B=∠C,∴△APB∽△DPC,∴=,∴需要测量线段AB的长度.
10.如图,一艘轮船在A处测得灯塔P位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是( B )
A.15海里 B.30海里 C.45海里 D.30海里
第10题图 第11题图
11.【中考·兰州】如图,小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE=BC=0.5 m,A,B,C三点共线),把一面镜子水平放置在平台上的点G处,测得CG=15 m.
然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得EG=3 m,小明身高EF=1.6 m,则凉亭的高度AB约为( A )
A.8.5 m B.9 m C.9.5 m D.10 m
【点拨】由题意知∠AGC=∠FGE.
∵∠ACG=∠FEG=90°,
∴△ACG∽△FEG.
∴=.∴=.∴AC=8 m.
∴AB=AC+BC=8+0.5=8.5(m).
12.【2021·绍兴】如图,树AB在路灯O的照射下形成投影AC,已知路灯高PO=5 m,树影AC=3 m,树AB与路灯O的水平距离AP=4.5 m,则树的高度AB是( A )
A.2 m B.3 m C. m D. m
第12题图 第13题图
13.【中考·毕节】如图,在一块斜边长30 cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF∶AC=1∶3,则这块木板截取正方形CDEF后,剩余部分的面积为( )
A.100 cm2 B.150 cm2 C.170 cm2 D.200 cm2
【点拨】设AF=x cm,则AC=3x cm.
∵四边形CDEF为正方形,∴EF=CF=2x cm,EF∥BC,
∴△AEF∽△ABC,∴==,∴BC=6x cm.
在Rt△ABC中,AB2=AC2+BC2,即302=(3x)2+(6x)2,
解得x=2(负值已舍去),
∴CF=4 cm,AC=6 cm,BC=12 cm,
∴剩余部分的面积=×12×6-4×4=100(cm2).
【答案】A
二、填空题
14.某数学兴趣小组来到城关区时代广场,设计用手电来测量广场附近某大厦CD的高度,如图,点P处放一水平的平面镜.光线从点A出发经平面镜反射后刚好射到大厦CD的顶端C处.已知AB⊥BD,CD⊥BD,测得AB=1.5米,BP=2米,PD=52米,那么该大厦的高度为 39 米.
第14题图 第15题图 第16题图
15.如图,李老师用自制的直角三角形纸板去测量“步云阁”的高度,他调整自己的位置,设法使斜边DF保持水平,边DE与点B在同一直线上.已知直角三角纸板中DE=16 cm,EF=12 cm,测得眼睛D离地面的高度为1.8米,他与“步云阁”的水平距离CD为104 m,则“步云阁”的高度AB是 79.8 米.
16.如图,△ABC是测量小玻璃管内径的量具,AB的长为18 cm,AC被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(点D,E分别在AC,BC上,且DE∥AB),那么小玻璃管内径DE是 12 cm.
17.《九章算术》是我国古代数学名著,书中有下列问题:今有勾五步,股十二步,问勾中容方几何 其意思为:今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步 该问题的答案是 步.
第17题图 第18题图 第19题图
18.【2021·吉林】如图,为了测量山坡的护坡石坝高,把一根长为4.5 m的竹竿AC斜靠在石坝旁,量出竿上AD长为1 m时,它离地面的高度DE为0.6 m,则坝高CF为 m.
【答案】2.7
【解析】由题意,得DE∥CF,∴△ADE∽△ACF,∴=,即=,∴CF=2.7 m.
19.【2021烟台期末】如图,EB为驾驶员的盲区,驾驶员的眼睛点P处到地面BE的距离为1.6米,车头FACD近似看成一个矩形,且满足3FD=2FA,若盲区EB的长度是6米,则车宽FA为 米.
【答案】
【解析】如图,过点P作PM⊥BE,垂足为M,交AF于点N,则PM=1.6米,设FA=x米,由3FD=2FA,得FD=x=MN.∵四边形ACDF是矩形,∴AF∥CD,∴△PAF∽△PBE,∴=,即=,∴PN=x.∵PN+MN=PM,∴x+x=1.6,解得x=,故FA= 米.
三、解答题
20.《孙子算经》中有道歌谣算题:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸.问竿长几何 其意思为:有一根竹竿不知道有多长,量出它在太阳下的影长为一丈五尺.同时立一根一尺五寸的小标杆,它的影长为五寸.请你算一算竹竿的长度是多少.(其中丈和尺是古代的长度单位,1丈=10尺,1尺=10寸)
解:设竹竿的长度为x尺.
依题意,得,解得x=45.
答:竹竿的长度是45尺.
21.如图,建筑物BC上有一个旗杆AB,小芳计划用学过的知识测量该建筑物的高度,测量方法如下:在该建筑物底部所在的平地上有一棵小树FD,小芳沿CD后退,发现地面上的点E、树顶F、旗杆顶端A恰好在一条直线上,继续后退,发现地面上的点G、树顶F、建筑物顶端B恰好在一条直线上.已知旗杆AB=3米,FD=4米,DE=5米,EG=1.5米,点A,B,C在一条直线上,点C,D,E,G在一条直线上,AC,FD均垂直于CG,请你帮助小芳求出这座建筑物的高BC.
解:由题知∠ACE=∠FDE=90°,∠AEC=∠FED,
∴△ACE∽△FDE,∴. ①
又∵∠BCG=∠FDG=90°,∠BGC=∠FGD,
∴△BCG∽△FDG,∴. ②
联立①②,得BC=14.
答:这座建筑物的高BC为14米.
22.如图,李明用自制的直角三角形纸板去测量“步云阁”的高度,他调整自己的位置,设法使斜边DF保持水平,边DE与点B在同一直线上,已知直角三角形纸板中DE=16 cm,EF=12 cm,测得眼睛D离地面的高度为1.8 m,他与“步云阁”的水平距离CD为104 m,求“步云阁”的高度AB.
【解析】 在△DEF和△DCB中,∠D=∠D,∠DEF=∠DCB=90°,
∴△DEF∽△DCB,∴=,即=,∴BC=78 m.
∵AC=1.8 m,∴AB=AC+BC=79.8 m.
答:“步云阁”的高度AB为79.8 m.
23.如图,小华和同伴春游时,发现在某地小山坡的点E处有一棵小桃树,他们想利用皮尺、测角仪和平面镜测量小桃树到山脚下的距离(即DE的长度),小华站在点B处,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E,且测得BC=6米,CD=24米,∠CDE=135°.已知小华的眼睛距地面的高度AB=1.5米,请根据以上数据,求DE的长度.(结果保留根号)
【解析】 如图,过点E作EF⊥BC于点F,
∵∠CDE=135°,∴∠EDF=45°,∴DF=EF.
设EF=x米,则DF=x米,DE=x米,
∵∠B=∠EFC=90°,∠ACB=∠ECD,
∴△ABC∽△EFC,∴=,
即=,∴x=8,∴DE=8 米,
故DE的长度为8 米.
24.青龙寺是西安最著名的樱花观赏地,樱花品种达到了13种之多,每年3,4月陆续开放的樱花让这里成了花的海洋.一天,小明和小刚去青龙寺游玩,想利用所学知识测量一棵樱花树的高度(樱花树四周被围起来了,底部不易到达).小明在F处竖立了一根标杆EF,小刚走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上.此时测得小刚的眼睛到地面的距离DC=1.6米;然后,小刚在C处蹲下,小明平移标杆到H处时,小刚恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小刚的眼睛到地面的距离MC=0.8米.已知EF=GH=2.4米,CF=2米,FH=1.6米,点C,F,H,A在一条直线上,点M在CD上,CD⊥AC,EF⊥AC,GH⊥AC,AB⊥AC.根据以上测量过程及测量数据,请你求出这棵樱花树AB的高度.
【解析】 如图,过点D作DP⊥AB于点P,交EF于点N,过点M作MQ⊥AB于点Q,交GH于点K,
由题意,得DP=MQ=AC,DN=CF=2米,MK=CH,AP=DC=1.6米,AQ=HK=MC=0.8米.
∵∠EDN=∠BDP,∠END=∠BPD=90°,∠GMK=∠BMQ,∠GKM=∠BQM=90°,∴△DEN∽△DBP,△GMK∽△BMQ,
∴=,=,∴=,=,
∴AB=8.8米.
答:这棵樱花树AB的高度是8.8米.
25.小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)如图1,垂直于地面放置的正方形框架ABCD,边长AB为30 cm,在其正上方有一个灯泡,在灯泡的照射下,正方形框架的横向影子A'B,D'C的长度和为6 cm,那么灯泡离地面的高度为180cm.
(2)不改变图1中灯泡的高度,将两个边长为30 cm的正方形框架按图2摆放,灯泡仍处于两个正方形的正上方.请计算此时横向影子A'B,D'C的长度和为多少
(3)有n个边长为a的正方形按图3摆放,测得横向影子A'B,D'C的长度和为b,灯泡处于n个正方形的正上方.求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
解:(2)设横向影子A'B,D'C的长度和为y cm,灯泡的位置为点P.
∵AD∥A'D',∴∠PAD=∠PA'D',∠PDA=∠PD'A',
∴△PAD∽△PA'D'.
根据相似三角形对应高的比等于相似比的性质,可得,
∴,解得y=12.
∴此时横向影子A'B,D'C的长度和为12 cm.
(3)设灯泡离地面的距离为x,记灯泡为点P.
由题意得PM=x,PN=x-a,AD=na,A'D'=na+b,同理可得,
∴灯泡离地面的距离为.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
