27.3.1 位似图形 同步练习(含答案)
文档属性
| 名称 | 27.3.1 位似图形 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 16:46:00 | ||
图片预览



文档简介
27.3 位 似
第1课时 位似图形
一、选择题
1.下列判断中,正确的是( )
A.相似图形一定是位似图形 B.位似图形一定是相似图形
C.全等的图形一定是位似图形 D.位似图形一定是全等的图形
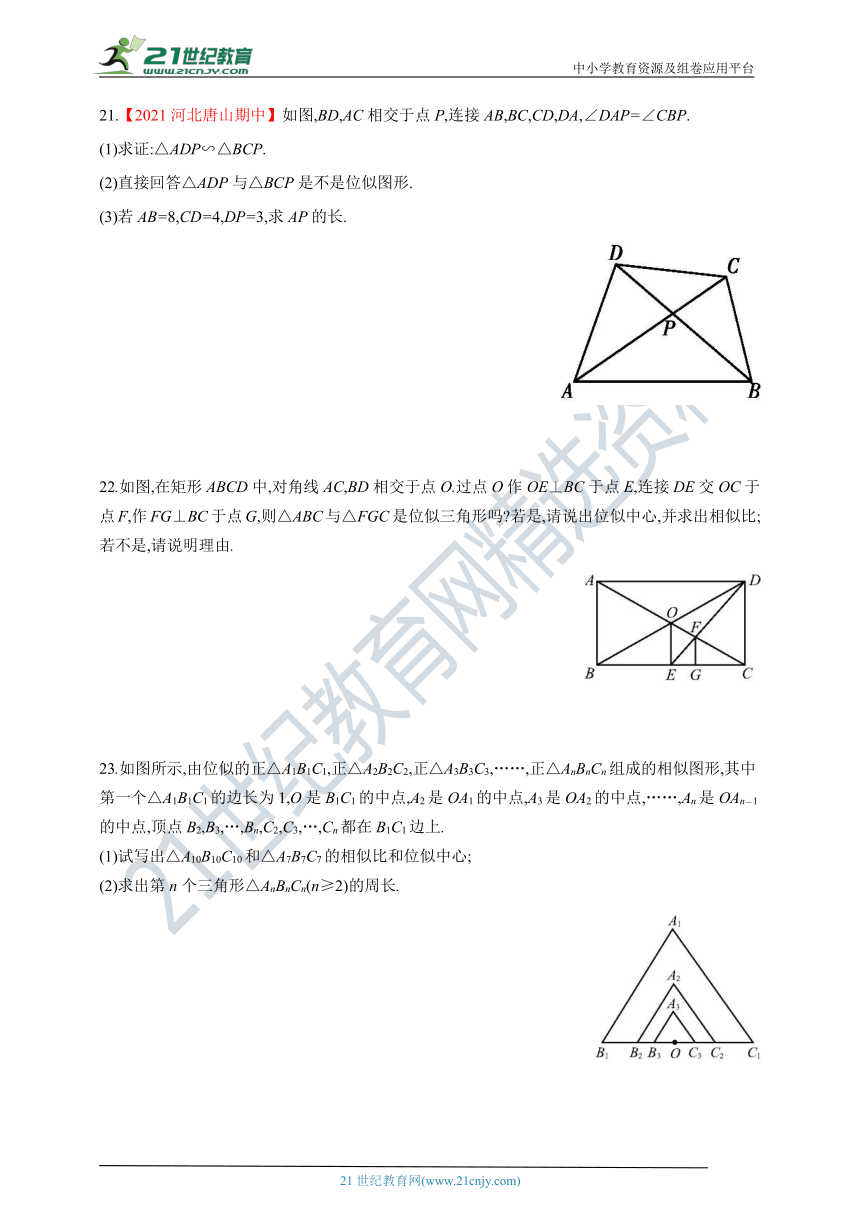
2.下列各选项中的两个图形不是位似图形的是( )
3.【2021·温州】如图,图形甲与图形乙是位似图形,O是位似中心,位似比为2∶3,点A,B的对应点分别为点A′,B′.若AB=6,则A′B′的长为( )
A.8 B.9 C.10 D.15
第3题图 第4题图 第5题图
4.如图,四边形ABCD与四边形A'B'C'D'位似,点O为位似中心.若OB∶OB'=2∶3,则四边形ABCD与四边形A'B'C'D'的面积比为( )
A.2∶3 B.2∶5 C.4∶9 D.4∶25
5.【2021山东菏泽牡丹区三模】如图,以点O为位似中心,把△ABC放大为原来的2倍得到△A'B'C'.下列说法错误的是( )
A.△ABC∽△A'B'C' B.点C,O,C'在同一条直线上
C.AO∶AA'=1∶2 D.AB∥A'B'
6.【2021重庆南开中学月考】如图,四边形ABCD与四边形EFGH位似,位似中心是O,若OA∶OE=1∶3,且四边形ABCD的周长为4,则四边形EFGH的周长为( )
A.12 B.16 C.20 D.24
第6题图 第9题图 第10题图
7.如图,下列位似图形中,面积比是1∶9的是 ( )
OA=OA′ OA=AA′ OA=2AA′ OA=AA′
A B C D
8.如图,△ABO与△A′B′O是位似图形,其中AB∥A′B′,则A′B′的长y与AB的长x之间函数关系的图象大致是( )
9.如图,矩形EFGO的两边在坐标轴上,O为平面直角坐标系的原点,以y轴上的某一点为位似中心,作位似图形ABCD,且点B,F的坐标分别为(-4,4),(2,1),则位似中心的坐标为( )
A.(0,3) B.(0,2.5) C.(0,2) D.(0,1.5)
10.图中两个四边形是位似图形,它们的位似中心是( )
A.点M B.点N C.点O D.点P
11.如图,四边形ABCD与四边形A'B'C'D'位似,点O为位似中心.若OA∶AA'=1∶2,则四边形ABCD与四边形A'B'C'D'的面积比为( )
A.1∶4 B.1∶2 C.1∶9 D.1∶3
第11题图 第12题图 第13题图 第14题图
12.如图,点O是等边△PQR的中心,P',Q',R'分别是OP,OQ,OR的中点,则△P'Q'R'与△PQR是位似三角形,此时△P'Q'R'与△PQR的相似比、位似中心分别是( )
A.2,点P B.,点P C.2,点O D.,点O
二、填空题
13.如图,E,F,G,H分别是OA,OB,OC,OD的中点.已知四边形EFGH的面积是3,则四边形ABCD的面积是 .
14.【2020·兰州】如图,四边形ABCD与四边形A′B′C′D′位似,位似中心为点O,OC=6,CC′=4,AB=3,则A′B′=________.
15.如图,已知△ABC,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的是 .(填序号)
①△ABC与△DEF是位似图形;
②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长之比为1∶2;
④△ABC与△DEF的面积之比为4∶1.
第15题图 第16题图 第17题图
16.如图,△ABC与△A1B1C1是以点O为位似中心的位似图形.若OA=3AA1,S△ABC=36,则= .
17.如图,正六边形OABCDE与正六边形OA'B'C'D'E'是关于原点O的位似图形,相似比为3∶2,已知点C'(6,0),则正六边形OABCDE的周长为 .
18.在△ABC中,AB=BC,∠B=90°,将△ABC沿BC方向平移,得到△A'CC',以点C为位似中心,作△DEC与△ABC位似,点D的位似点是点A,且相似比为1∶2.若F为CC'的中点,连接DF,A'F,则的值为 .
三、解答题
19.如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB'C'D',使它与四边形ABCD位似,且相似比为2.
(1)在图中画出四边形AB'C'D';
(2)填空:连接AC',则∠AC'D'= .
20.如图,△DEF是△ABC经过位似变换得到的,位似中心是点O,请确定点O的位置,如果OC=3.6 cm,OF=2.4 cm,求它们的相似比.
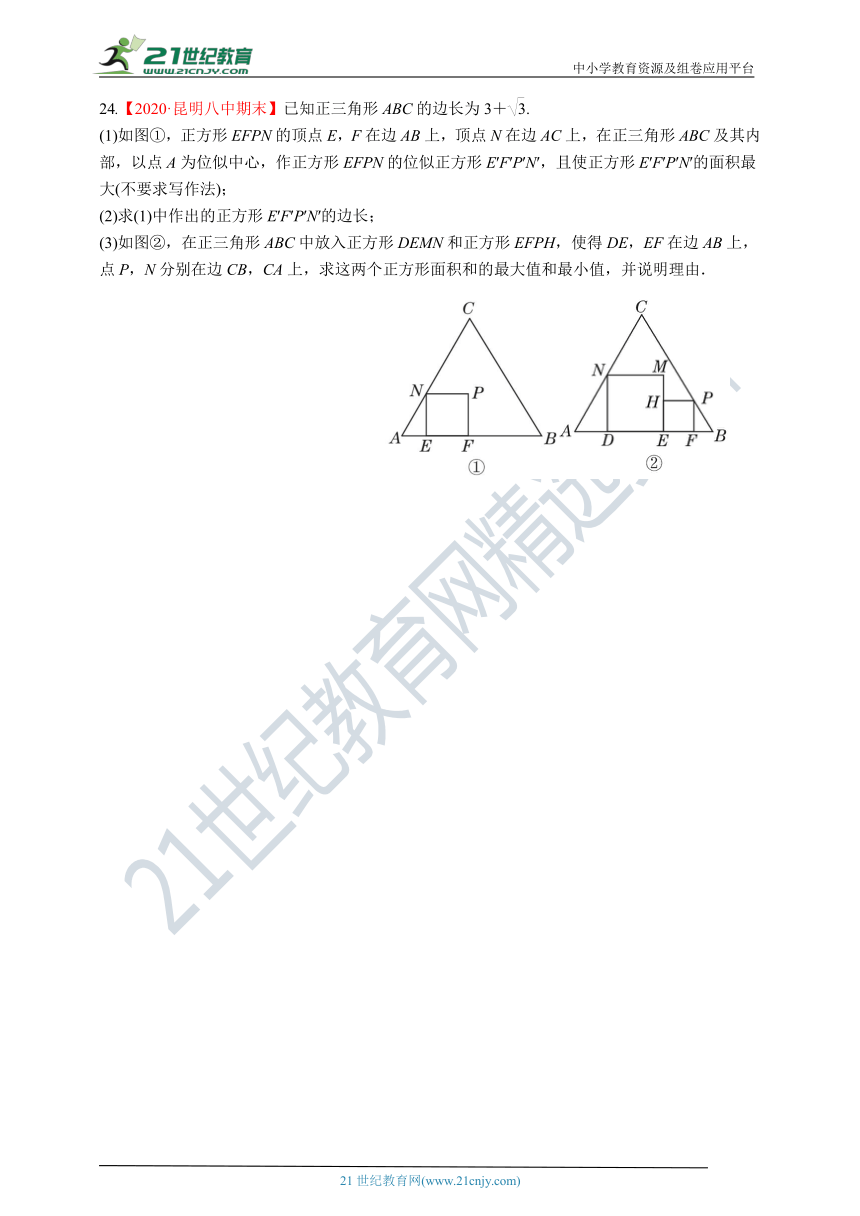
21.【2021河北唐山期中】如图,BD,AC相交于点P,连接AB,BC,CD,DA,∠DAP=∠CBP.
(1)求证:△ADP∽△BCP.
(2)直接回答△ADP与△BCP是不是位似图形.
(3)若AB=8,CD=4,DP=3,求AP的长.
22.如图,在矩形ABCD中,对角线AC,BD相交于点O.过点O作OE⊥BC于点E,连接DE交OC于点F,作FG⊥BC于点G,则△ABC与△FGC是位似三角形吗 若是,请说出位似中心,并求出相似比;若不是,请说明理由.
23.如图所示,由位似的正△A1B1C1,正△A2B2C2,正△A3B3C3,……,正△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,O是B1C1的中点,A2是OA1的中点,A3是OA2的中点,……,An是OAn-1的中点,顶点B2,B3,…,Bn,C2,C3,…,Cn都在B1C1边上.
(1)试写出△A10B10C10和△A7B7C7的相似比和位似中心;
(2)求出第n个三角形△AnBnCn(n≥2)的周长.
24.【2020·昆明八中期末】已知正三角形ABC的边长为3+.
(1)如图①,正方形EFPN的顶点E,F在边AB上,顶点N在边AC上,在正三角形ABC及其内部,以点A为位似中心,作正方形EFPN的位似正方形E′F′P′N′,且使正方形E′F′P′N′的面积最大(不要求写作法);
(2)求(1)中作出的正方形E′F′P′N′的边长;
(3)如图②,在正三角形ABC中放入正方形DEMN和正方形EFPH,使得DE,EF在边AB上,点P,N分别在边CB,CA上,求这两个正方形面积和的最大值和最小值,并说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.下列判断中,正确的是( B )
A.相似图形一定是位似图形 B.位似图形一定是相似图形
C.全等的图形一定是位似图形 D.位似图形一定是全等的图形
2.下列各选项中的两个图形不是位似图形的是( D )
3.【2021·温州】如图,图形甲与图形乙是位似图形,O是位似中心,位似比为2∶3,点A,B的对应点分别为点A′,B′.若AB=6,则A′B′的长为( B )
A.8 B.9 C.10 D.15
第3题图 第4题图 第5题图
4.如图,四边形ABCD与四边形A'B'C'D'位似,点O为位似中心.若OB∶OB'=2∶3,则四边形ABCD与四边形A'B'C'D'的面积比为( C )
A.2∶3 B.2∶5 C.4∶9 D.4∶25
5.【2021山东菏泽牡丹区三模】如图,以点O为位似中心,把△ABC放大为原来的2倍得到△A'B'C'.下列说法错误的是( )
A.△ABC∽△A'B'C' B.点C,O,C'在同一条直线上
C.AO∶AA'=1∶2 D.AB∥A'B'
【答案】C
【解析】∵以点O为位似中心,把△ABC放大为原来的2倍得到△A'B'C',∴OA∶OA'=1∶2,∴AO∶AA'=1∶3,故C错误.
6.【2021重庆南开中学月考】如图,四边形ABCD与四边形EFGH位似,位似中心是O,若OA∶OE=1∶3,且四边形ABCD的周长为4,则四边形EFGH的周长为( )
A.12 B.16 C.20 D.24
【答案】A
【解析】因为四边形ABCD与四边形EFGH位似,OA∶OE=1∶3,所以四边形ABCD的周长∶四边形EFGH的周长=1∶3.因为四边形ABCD的周长为4,所以四边形EFGH的周长为12.
第6题图 第9题图 第10题图
7.如图,下列位似图形中,面积比是1∶9的是 ( D )
OA=OA′ OA=AA′ OA=2AA′ OA=AA′
A B C D
8.如图,△ABO与△A′B′O是位似图形,其中AB∥A′B′,则A′B′的长y与AB的长x之间函数关系的图象大致是( C )
9.如图,矩形EFGO的两边在坐标轴上,O为平面直角坐标系的原点,以y轴上的某一点为位似中心,作位似图形ABCD,且点B,F的坐标分别为(-4,4),(2,1),则位似中心的坐标为( C )
A.(0,3) B.(0,2.5) C.(0,2) D.(0,1.5)
10.图中两个四边形是位似图形,它们的位似中心是( D )
A.点M B.点N C.点O D.点P
11.如图,四边形ABCD与四边形A'B'C'D'位似,点O为位似中心.若OA∶AA'=1∶2,则四边形ABCD与四边形A'B'C'D'的面积比为( C )
A.1∶4 B.1∶2 C.1∶9 D.1∶3
第11题图 第12题图 第13题图 第14题图
12.如图,点O是等边△PQR的中心,P',Q',R'分别是OP,OQ,OR的中点,则△P'Q'R'与△PQR是位似三角形,此时△P'Q'R'与△PQR的相似比、位似中心分别是( D )
A.2,点P B.,点P C.2,点O D.,点O
二、填空题
13.如图,E,F,G,H分别是OA,OB,OC,OD的中点.已知四边形EFGH的面积是3,则四边形ABCD的面积是 12 .
14.【2020·兰州】如图,四边形ABCD与四边形A′B′C′D′位似,位似中心为点O,OC=6,CC′=4,AB=3,则A′B′=________.
【答案】5
15.如图,已知△ABC,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的是 .(填序号)
①△ABC与△DEF是位似图形;
②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长之比为1∶2;
④△ABC与△DEF的面积之比为4∶1.
【答案】①②④
第15题图 第16题图 第17题图
16.如图,△ABC与△A1B1C1是以点O为位似中心的位似图形.若OA=3AA1,S△ABC=36,则= .
【答案】64
【解析】∵△ABC与△A1B1C1是以点O为位似中心的位似图形,∴△ABC∽△A1B1C1.∵OA=3AA1,∴△ABC与△A1B1C1的相似比为
OA∶OA1=3∶4,∴=()2=()2=.∵S△ABC=36,∴=64.
17.如图,正六边形OABCDE与正六边形OA'B'C'D'E'是关于原点O的位似图形,相似比为3∶2,已知点C'(6,0),则正六边形OABCDE的周长为 27 .
18.在△ABC中,AB=BC,∠B=90°,将△ABC沿BC方向平移,得到△A'CC',以点C为位似中心,作△DEC与△ABC位似,点D的位似点是点A,且相似比为1∶2.若F为CC'的中点,连接DF,A'F,则的值为 1或 .
提示:设AB=BC=2x,分点D在AC上和点D在AC的延长线上两种情况进行讨论.
三、解答题
19.如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB'C'D',使它与四边形ABCD位似,且相似比为2.
(1)在图中画出四边形AB'C'D';
(2)填空:连接AC',则∠AC'D'= 45° .
解:(1)图略.
20.如图,△DEF是△ABC经过位似变换得到的,位似中心是点O,请确定点O的位置,如果OC=3.6 cm,OF=2.4 cm,求它们的相似比.
解:连接AD,CF交于点O,则点O即为所求,图略.
∵OC=3.6 cm,OF=2.4 cm,
∴OC∶OF=3∶2,
∴△ABC与△DEF的相似比为3∶2.
21.【2021河北唐山期中】如图,BD,AC相交于点P,连接AB,BC,CD,DA,∠DAP=∠CBP.
(1)求证:△ADP∽△BCP.
(2)直接回答△ADP与△BCP是不是位似图形.
(3)若AB=8,CD=4,DP=3,求AP的长.
【解析】(1)∵∠DAP=∠CBP,∠DPA=∠CPB,
∴△ADP∽△BCP.
(2)△ADP与△BCP不是位似图形.
(3)由(1)知△ADP∽△BCP,∴=,
又∠APB=∠CPD,∴△APB∽△DPC,
∴=,即=,∴AP=6.
22.如图,在矩形ABCD中,对角线AC,BD相交于点O.过点O作OE⊥BC于点E,连接DE交OC于点F,作FG⊥BC于点G,则△ABC与△FGC是位似三角形吗 若是,请说出位似中心,并求出相似比;若不是,请说明理由.
解:△ABC与△FGC是位似三角形,点C是位似中心,相似比为3∶1.
理由:∵在矩形ABCD中,对角线AC,BD相交于点O,OE⊥BC,∴.
由题意可得EO∥FG,则,
∴,即△ABC与△FGC的相似比为3∶1.
23.如图所示,由位似的正△A1B1C1,正△A2B2C2,正△A3B3C3,……,正△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,O是B1C1的中点,A2是OA1的中点,A3是OA2的中点,……,An是OAn-1的中点,顶点B2,B3,…,Bn,C2,C3,…,Cn都在B1C1边上.
(1)试写出△A10B10C10和△A7B7C7的相似比和位似中心;
(2)求出第n个三角形△AnBnCn(n≥2)的周长.
解:(1)∵△A1B1C1的边长为1,O是B1C1的中点,A2是OA1的中点,
∴正△A2B2C2的边长为,
∴正△A10B10C10和正△A7B7C7的相似比=,它们的位似中心为点O.
(2)∵第n个三角形△AnBnCn(n≥2)的边长为,
∴第n个三角形△AnBnCn(n≥2)的周长为.
24.【2020·昆明八中期末】已知正三角形ABC的边长为3+.
(1)如图①,正方形EFPN的顶点E,F在边AB上,顶点N在边AC上,在正三角形ABC及其内部,以点A为位似中心,作正方形EFPN的位似正方形E′F′P′N′,且使正方形E′F′P′N′的面积最大(不要求写作法);
解:如图①,正方形E′F′P′N′即为所求.
(2)求(1)中作出的正方形E′F′P′N′的边长;
解:设正方形E′F′P′N′的边长为x.
∵△ABC为正三角形,∴AE′=BF′=x.
∵E′F′+AE′+BF′=AB,∴x+x+x=3+,
∴x=,即x=3-3.
∴正方形E′F′P′N′的边长为3-3.
(3)如图②,在正三角形ABC中放入正方形DEMN和正方形EFPH,使得DE,EF在边AB上,点P,N分别在边CB,CA上,求这两个正方形面积和的最大值和最小值,并说明理由.
解:这两个正方形面积和的最大值是99-54,最小值是.理由如下:如图②,连结NE,EP,PN,则∠NEP=90°.
设正方形DEMN、正方形EFPH的边长分别为m,n(m≥n),它们的面积和为S,则NE=m,PE=n,
∴PN2=NE2+PE2=2m2+2n2=2(m2+n2),
∴S=m2+n2=PN2.
延长PH交ND于点G,则PG⊥ND.
在Rt△PGN中,PN2=PG2+GN2=(m+n)2+(m-n)2.
∵AD+DE+EF+BF=AB,
易得m+m+n+n=+3,化简得m+n=3.
∴S=[32+(m-n)2]=+(m-n)2.
①当(m-n)2=0时,即m=n时,S最小,∴S最小=;
②当(m-n)2最大时,S最大,即当m取最大值且n取最小值时,S最大.∵m+n=3,由(2)知,m最大=3-3,
可得n最大=6-3.∴S最大=[9+(m最大-n最小)2]
=[9+(3-3-6+3)2]=99-54.
综上所述,这两个正方形面积和的最大值是99-54,最小值是.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1课时 位似图形
一、选择题
1.下列判断中,正确的是( )
A.相似图形一定是位似图形 B.位似图形一定是相似图形
C.全等的图形一定是位似图形 D.位似图形一定是全等的图形
2.下列各选项中的两个图形不是位似图形的是( )
3.【2021·温州】如图,图形甲与图形乙是位似图形,O是位似中心,位似比为2∶3,点A,B的对应点分别为点A′,B′.若AB=6,则A′B′的长为( )
A.8 B.9 C.10 D.15
第3题图 第4题图 第5题图
4.如图,四边形ABCD与四边形A'B'C'D'位似,点O为位似中心.若OB∶OB'=2∶3,则四边形ABCD与四边形A'B'C'D'的面积比为( )
A.2∶3 B.2∶5 C.4∶9 D.4∶25
5.【2021山东菏泽牡丹区三模】如图,以点O为位似中心,把△ABC放大为原来的2倍得到△A'B'C'.下列说法错误的是( )
A.△ABC∽△A'B'C' B.点C,O,C'在同一条直线上
C.AO∶AA'=1∶2 D.AB∥A'B'
6.【2021重庆南开中学月考】如图,四边形ABCD与四边形EFGH位似,位似中心是O,若OA∶OE=1∶3,且四边形ABCD的周长为4,则四边形EFGH的周长为( )
A.12 B.16 C.20 D.24
第6题图 第9题图 第10题图
7.如图,下列位似图形中,面积比是1∶9的是 ( )
OA=OA′ OA=AA′ OA=2AA′ OA=AA′
A B C D
8.如图,△ABO与△A′B′O是位似图形,其中AB∥A′B′,则A′B′的长y与AB的长x之间函数关系的图象大致是( )
9.如图,矩形EFGO的两边在坐标轴上,O为平面直角坐标系的原点,以y轴上的某一点为位似中心,作位似图形ABCD,且点B,F的坐标分别为(-4,4),(2,1),则位似中心的坐标为( )
A.(0,3) B.(0,2.5) C.(0,2) D.(0,1.5)
10.图中两个四边形是位似图形,它们的位似中心是( )
A.点M B.点N C.点O D.点P
11.如图,四边形ABCD与四边形A'B'C'D'位似,点O为位似中心.若OA∶AA'=1∶2,则四边形ABCD与四边形A'B'C'D'的面积比为( )
A.1∶4 B.1∶2 C.1∶9 D.1∶3
第11题图 第12题图 第13题图 第14题图
12.如图,点O是等边△PQR的中心,P',Q',R'分别是OP,OQ,OR的中点,则△P'Q'R'与△PQR是位似三角形,此时△P'Q'R'与△PQR的相似比、位似中心分别是( )
A.2,点P B.,点P C.2,点O D.,点O
二、填空题
13.如图,E,F,G,H分别是OA,OB,OC,OD的中点.已知四边形EFGH的面积是3,则四边形ABCD的面积是 .
14.【2020·兰州】如图,四边形ABCD与四边形A′B′C′D′位似,位似中心为点O,OC=6,CC′=4,AB=3,则A′B′=________.
15.如图,已知△ABC,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的是 .(填序号)
①△ABC与△DEF是位似图形;
②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长之比为1∶2;
④△ABC与△DEF的面积之比为4∶1.
第15题图 第16题图 第17题图
16.如图,△ABC与△A1B1C1是以点O为位似中心的位似图形.若OA=3AA1,S△ABC=36,则= .
17.如图,正六边形OABCDE与正六边形OA'B'C'D'E'是关于原点O的位似图形,相似比为3∶2,已知点C'(6,0),则正六边形OABCDE的周长为 .
18.在△ABC中,AB=BC,∠B=90°,将△ABC沿BC方向平移,得到△A'CC',以点C为位似中心,作△DEC与△ABC位似,点D的位似点是点A,且相似比为1∶2.若F为CC'的中点,连接DF,A'F,则的值为 .
三、解答题
19.如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB'C'D',使它与四边形ABCD位似,且相似比为2.
(1)在图中画出四边形AB'C'D';
(2)填空:连接AC',则∠AC'D'= .
20.如图,△DEF是△ABC经过位似变换得到的,位似中心是点O,请确定点O的位置,如果OC=3.6 cm,OF=2.4 cm,求它们的相似比.
21.【2021河北唐山期中】如图,BD,AC相交于点P,连接AB,BC,CD,DA,∠DAP=∠CBP.
(1)求证:△ADP∽△BCP.
(2)直接回答△ADP与△BCP是不是位似图形.
(3)若AB=8,CD=4,DP=3,求AP的长.
22.如图,在矩形ABCD中,对角线AC,BD相交于点O.过点O作OE⊥BC于点E,连接DE交OC于点F,作FG⊥BC于点G,则△ABC与△FGC是位似三角形吗 若是,请说出位似中心,并求出相似比;若不是,请说明理由.
23.如图所示,由位似的正△A1B1C1,正△A2B2C2,正△A3B3C3,……,正△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,O是B1C1的中点,A2是OA1的中点,A3是OA2的中点,……,An是OAn-1的中点,顶点B2,B3,…,Bn,C2,C3,…,Cn都在B1C1边上.
(1)试写出△A10B10C10和△A7B7C7的相似比和位似中心;
(2)求出第n个三角形△AnBnCn(n≥2)的周长.
24.【2020·昆明八中期末】已知正三角形ABC的边长为3+.
(1)如图①,正方形EFPN的顶点E,F在边AB上,顶点N在边AC上,在正三角形ABC及其内部,以点A为位似中心,作正方形EFPN的位似正方形E′F′P′N′,且使正方形E′F′P′N′的面积最大(不要求写作法);
(2)求(1)中作出的正方形E′F′P′N′的边长;
(3)如图②,在正三角形ABC中放入正方形DEMN和正方形EFPH,使得DE,EF在边AB上,点P,N分别在边CB,CA上,求这两个正方形面积和的最大值和最小值,并说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.下列判断中,正确的是( B )
A.相似图形一定是位似图形 B.位似图形一定是相似图形
C.全等的图形一定是位似图形 D.位似图形一定是全等的图形
2.下列各选项中的两个图形不是位似图形的是( D )
3.【2021·温州】如图,图形甲与图形乙是位似图形,O是位似中心,位似比为2∶3,点A,B的对应点分别为点A′,B′.若AB=6,则A′B′的长为( B )
A.8 B.9 C.10 D.15
第3题图 第4题图 第5题图
4.如图,四边形ABCD与四边形A'B'C'D'位似,点O为位似中心.若OB∶OB'=2∶3,则四边形ABCD与四边形A'B'C'D'的面积比为( C )
A.2∶3 B.2∶5 C.4∶9 D.4∶25
5.【2021山东菏泽牡丹区三模】如图,以点O为位似中心,把△ABC放大为原来的2倍得到△A'B'C'.下列说法错误的是( )
A.△ABC∽△A'B'C' B.点C,O,C'在同一条直线上
C.AO∶AA'=1∶2 D.AB∥A'B'
【答案】C
【解析】∵以点O为位似中心,把△ABC放大为原来的2倍得到△A'B'C',∴OA∶OA'=1∶2,∴AO∶AA'=1∶3,故C错误.
6.【2021重庆南开中学月考】如图,四边形ABCD与四边形EFGH位似,位似中心是O,若OA∶OE=1∶3,且四边形ABCD的周长为4,则四边形EFGH的周长为( )
A.12 B.16 C.20 D.24
【答案】A
【解析】因为四边形ABCD与四边形EFGH位似,OA∶OE=1∶3,所以四边形ABCD的周长∶四边形EFGH的周长=1∶3.因为四边形ABCD的周长为4,所以四边形EFGH的周长为12.
第6题图 第9题图 第10题图
7.如图,下列位似图形中,面积比是1∶9的是 ( D )
OA=OA′ OA=AA′ OA=2AA′ OA=AA′
A B C D
8.如图,△ABO与△A′B′O是位似图形,其中AB∥A′B′,则A′B′的长y与AB的长x之间函数关系的图象大致是( C )
9.如图,矩形EFGO的两边在坐标轴上,O为平面直角坐标系的原点,以y轴上的某一点为位似中心,作位似图形ABCD,且点B,F的坐标分别为(-4,4),(2,1),则位似中心的坐标为( C )
A.(0,3) B.(0,2.5) C.(0,2) D.(0,1.5)
10.图中两个四边形是位似图形,它们的位似中心是( D )
A.点M B.点N C.点O D.点P
11.如图,四边形ABCD与四边形A'B'C'D'位似,点O为位似中心.若OA∶AA'=1∶2,则四边形ABCD与四边形A'B'C'D'的面积比为( C )
A.1∶4 B.1∶2 C.1∶9 D.1∶3
第11题图 第12题图 第13题图 第14题图
12.如图,点O是等边△PQR的中心,P',Q',R'分别是OP,OQ,OR的中点,则△P'Q'R'与△PQR是位似三角形,此时△P'Q'R'与△PQR的相似比、位似中心分别是( D )
A.2,点P B.,点P C.2,点O D.,点O
二、填空题
13.如图,E,F,G,H分别是OA,OB,OC,OD的中点.已知四边形EFGH的面积是3,则四边形ABCD的面积是 12 .
14.【2020·兰州】如图,四边形ABCD与四边形A′B′C′D′位似,位似中心为点O,OC=6,CC′=4,AB=3,则A′B′=________.
【答案】5
15.如图,已知△ABC,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的是 .(填序号)
①△ABC与△DEF是位似图形;
②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长之比为1∶2;
④△ABC与△DEF的面积之比为4∶1.
【答案】①②④
第15题图 第16题图 第17题图
16.如图,△ABC与△A1B1C1是以点O为位似中心的位似图形.若OA=3AA1,S△ABC=36,则= .
【答案】64
【解析】∵△ABC与△A1B1C1是以点O为位似中心的位似图形,∴△ABC∽△A1B1C1.∵OA=3AA1,∴△ABC与△A1B1C1的相似比为
OA∶OA1=3∶4,∴=()2=()2=.∵S△ABC=36,∴=64.
17.如图,正六边形OABCDE与正六边形OA'B'C'D'E'是关于原点O的位似图形,相似比为3∶2,已知点C'(6,0),则正六边形OABCDE的周长为 27 .
18.在△ABC中,AB=BC,∠B=90°,将△ABC沿BC方向平移,得到△A'CC',以点C为位似中心,作△DEC与△ABC位似,点D的位似点是点A,且相似比为1∶2.若F为CC'的中点,连接DF,A'F,则的值为 1或 .
提示:设AB=BC=2x,分点D在AC上和点D在AC的延长线上两种情况进行讨论.
三、解答题
19.如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB'C'D',使它与四边形ABCD位似,且相似比为2.
(1)在图中画出四边形AB'C'D';
(2)填空:连接AC',则∠AC'D'= 45° .
解:(1)图略.
20.如图,△DEF是△ABC经过位似变换得到的,位似中心是点O,请确定点O的位置,如果OC=3.6 cm,OF=2.4 cm,求它们的相似比.
解:连接AD,CF交于点O,则点O即为所求,图略.
∵OC=3.6 cm,OF=2.4 cm,
∴OC∶OF=3∶2,
∴△ABC与△DEF的相似比为3∶2.
21.【2021河北唐山期中】如图,BD,AC相交于点P,连接AB,BC,CD,DA,∠DAP=∠CBP.
(1)求证:△ADP∽△BCP.
(2)直接回答△ADP与△BCP是不是位似图形.
(3)若AB=8,CD=4,DP=3,求AP的长.
【解析】(1)∵∠DAP=∠CBP,∠DPA=∠CPB,
∴△ADP∽△BCP.
(2)△ADP与△BCP不是位似图形.
(3)由(1)知△ADP∽△BCP,∴=,
又∠APB=∠CPD,∴△APB∽△DPC,
∴=,即=,∴AP=6.
22.如图,在矩形ABCD中,对角线AC,BD相交于点O.过点O作OE⊥BC于点E,连接DE交OC于点F,作FG⊥BC于点G,则△ABC与△FGC是位似三角形吗 若是,请说出位似中心,并求出相似比;若不是,请说明理由.
解:△ABC与△FGC是位似三角形,点C是位似中心,相似比为3∶1.
理由:∵在矩形ABCD中,对角线AC,BD相交于点O,OE⊥BC,∴.
由题意可得EO∥FG,则,
∴,即△ABC与△FGC的相似比为3∶1.
23.如图所示,由位似的正△A1B1C1,正△A2B2C2,正△A3B3C3,……,正△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,O是B1C1的中点,A2是OA1的中点,A3是OA2的中点,……,An是OAn-1的中点,顶点B2,B3,…,Bn,C2,C3,…,Cn都在B1C1边上.
(1)试写出△A10B10C10和△A7B7C7的相似比和位似中心;
(2)求出第n个三角形△AnBnCn(n≥2)的周长.
解:(1)∵△A1B1C1的边长为1,O是B1C1的中点,A2是OA1的中点,
∴正△A2B2C2的边长为,
∴正△A10B10C10和正△A7B7C7的相似比=,它们的位似中心为点O.
(2)∵第n个三角形△AnBnCn(n≥2)的边长为,
∴第n个三角形△AnBnCn(n≥2)的周长为.
24.【2020·昆明八中期末】已知正三角形ABC的边长为3+.
(1)如图①,正方形EFPN的顶点E,F在边AB上,顶点N在边AC上,在正三角形ABC及其内部,以点A为位似中心,作正方形EFPN的位似正方形E′F′P′N′,且使正方形E′F′P′N′的面积最大(不要求写作法);
解:如图①,正方形E′F′P′N′即为所求.
(2)求(1)中作出的正方形E′F′P′N′的边长;
解:设正方形E′F′P′N′的边长为x.
∵△ABC为正三角形,∴AE′=BF′=x.
∵E′F′+AE′+BF′=AB,∴x+x+x=3+,
∴x=,即x=3-3.
∴正方形E′F′P′N′的边长为3-3.
(3)如图②,在正三角形ABC中放入正方形DEMN和正方形EFPH,使得DE,EF在边AB上,点P,N分别在边CB,CA上,求这两个正方形面积和的最大值和最小值,并说明理由.
解:这两个正方形面积和的最大值是99-54,最小值是.理由如下:如图②,连结NE,EP,PN,则∠NEP=90°.
设正方形DEMN、正方形EFPH的边长分别为m,n(m≥n),它们的面积和为S,则NE=m,PE=n,
∴PN2=NE2+PE2=2m2+2n2=2(m2+n2),
∴S=m2+n2=PN2.
延长PH交ND于点G,则PG⊥ND.
在Rt△PGN中,PN2=PG2+GN2=(m+n)2+(m-n)2.
∵AD+DE+EF+BF=AB,
易得m+m+n+n=+3,化简得m+n=3.
∴S=[32+(m-n)2]=+(m-n)2.
①当(m-n)2=0时,即m=n时,S最小,∴S最小=;
②当(m-n)2最大时,S最大,即当m取最大值且n取最小值时,S最大.∵m+n=3,由(2)知,m最大=3-3,
可得n最大=6-3.∴S最大=[9+(m最大-n最小)2]
=[9+(3-3-6+3)2]=99-54.
综上所述,这两个正方形面积和的最大值是99-54,最小值是.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
