河北省沙河市第一中学高二数学《共线向量与共面向量》课件
文档属性
| 名称 | 河北省沙河市第一中学高二数学《共线向量与共面向量》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 320.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-24 00:00:00 | ||
图片预览



文档简介
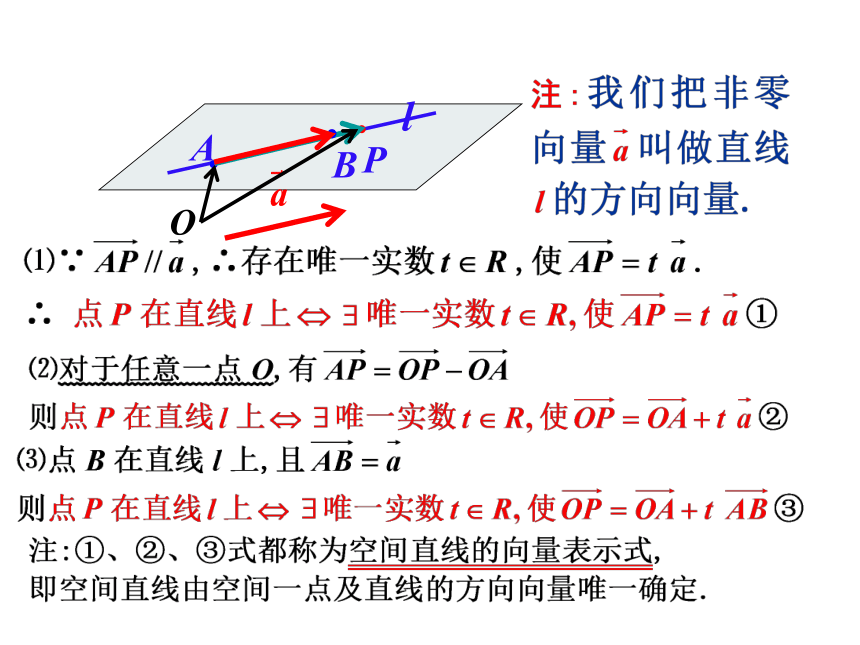
课件17张PPT。3.1.2 共线向量与共面向量APB平面向量基本定理:
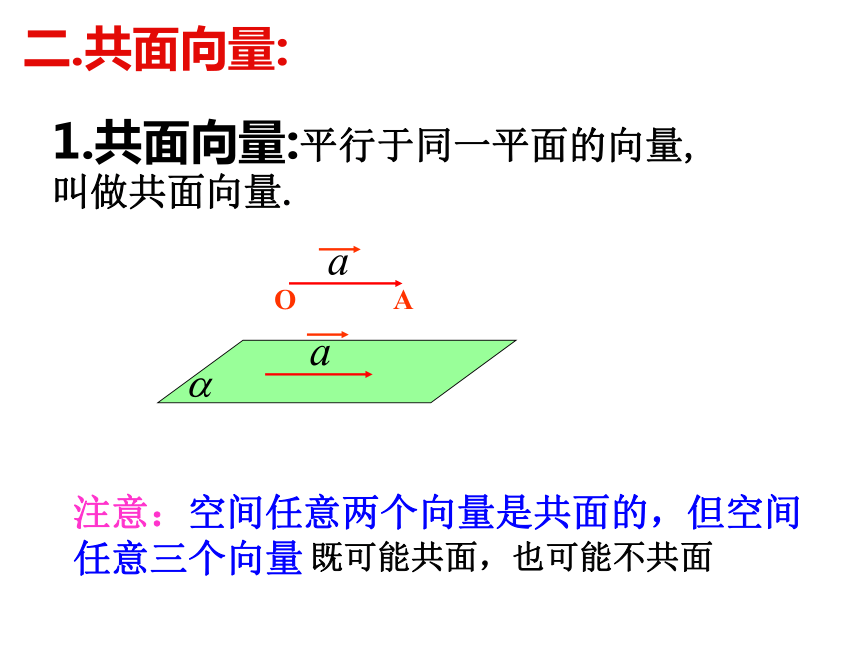
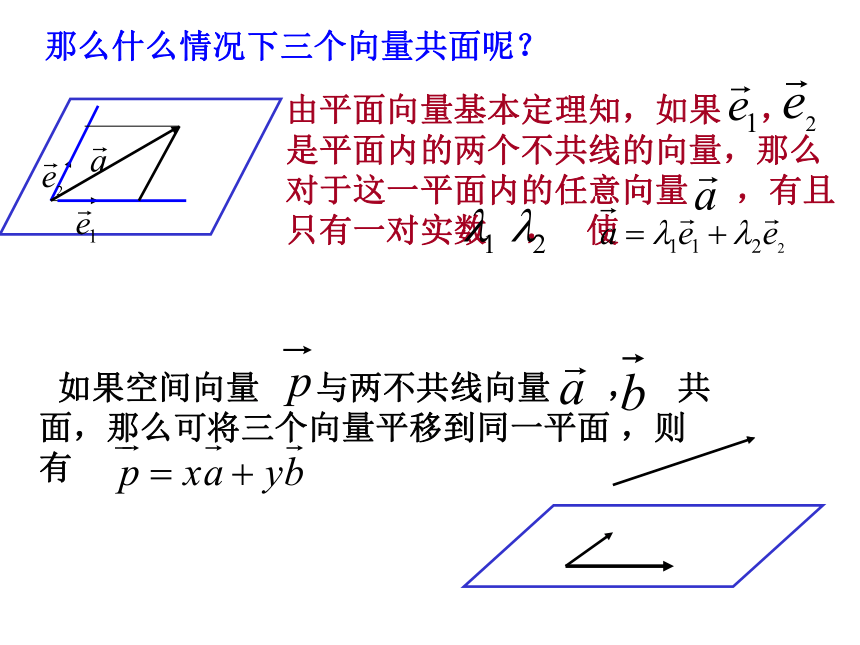
如果是 同一平面内两个不共线的向量,那么对于这一平面内的任一向量 ,有且只有一对实数 ,使1.共面向量:平行于同一平面的向量, 叫做共面向量.注意:空间任意两个向量是共面的,但空间任意三个向量既可能共面,也可能不共面二.共面向量:由平面向量基本定理知,如果 ,
是平面内的两个不共线的向量,那么
对于这一平面内的任意向量 ,有且只有一对实数 , 使 如果空间向量 与两不共线向量 , 共
面,那么可将三个向量平移到同一平面 ,则
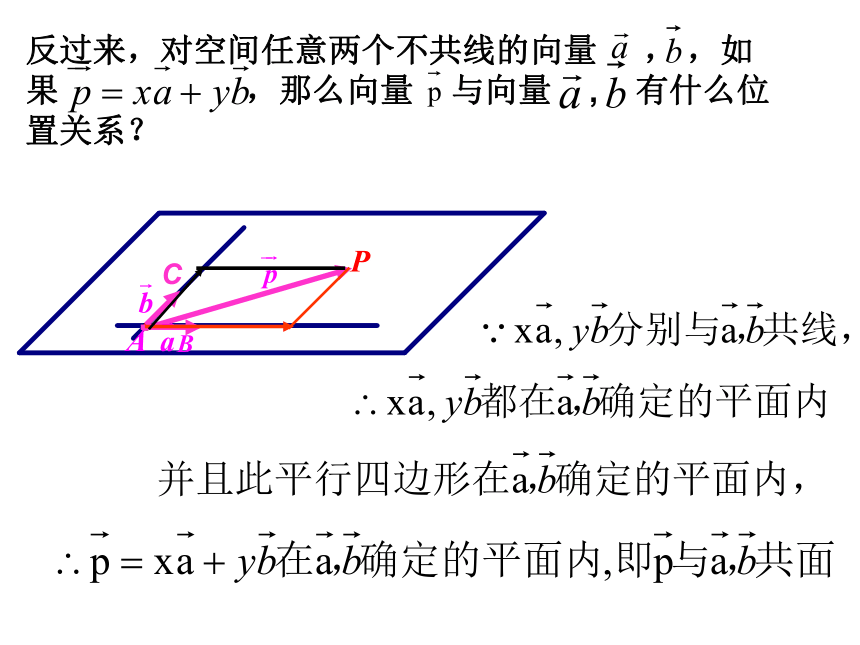
有 那么什么情况下三个向量共面呢?反过来,对空间任意两个不共线的向量 , ,如果 ,那么向量 与向量 , 有什么位
置关系?C2.共面向量定理:如果两个向量 , 不共线, 则向量 与向量 , 共面的充要条件是存在实数对x,y使C思考1:有平面ABC,若P点在此面内,须满足什么条件?可证明或判断四点共面或对空间任一点O,有1: 已知A、B、M三点不共线,对于平面
ABM外的任一点O,确定在下列各条件下,
点P是否与A、B、M一定共面?课堂练习一例1. 如图,已知平行四边形ABCD,过平
面AC外一点O作射线OA、OB、OC、OD,在四条射线上分别取点E、F、G、H,并且使
求证:
四点E、F、G、H共面;
OBAHGFECD例1 (课本例)已知 ABCD ,从平面AC外一点O引向量 求证:四点E、F、G、H共面;证明:(﹡)代入所以 E、F、G、H共面。1.下列说明正确的是: (A)在平面内共线的向量在空间不一定共线
(B)在空间共线的向量在平面内不一定共线
(C)在平面内共线的向量在空间一定不共线
(D)在空间共线的向量在平面内一定共线2.下列说法正确的是: (A)平面内的任意两个向量都共线
(B)空间的任意三个向量都不共面
(C)空间的任意两个向量都共面
(D)空间的任意三个向量都共面课堂练习二B课堂练习二4.已知点M在平面ABC内,并且对空间任
意一点O, ,则x
的值为:D5.已知A、B、C三点不共线,对平面外一点
O,在下列条件下,点P是否与A、B、C共面?小结共面
如果是 同一平面内两个不共线的向量,那么对于这一平面内的任一向量 ,有且只有一对实数 ,使1.共面向量:平行于同一平面的向量, 叫做共面向量.注意:空间任意两个向量是共面的,但空间任意三个向量既可能共面,也可能不共面二.共面向量:由平面向量基本定理知,如果 ,
是平面内的两个不共线的向量,那么
对于这一平面内的任意向量 ,有且只有一对实数 , 使 如果空间向量 与两不共线向量 , 共
面,那么可将三个向量平移到同一平面 ,则
有 那么什么情况下三个向量共面呢?反过来,对空间任意两个不共线的向量 , ,如果 ,那么向量 与向量 , 有什么位
置关系?C2.共面向量定理:如果两个向量 , 不共线, 则向量 与向量 , 共面的充要条件是存在实数对x,y使C思考1:有平面ABC,若P点在此面内,须满足什么条件?可证明或判断四点共面或对空间任一点O,有1: 已知A、B、M三点不共线,对于平面
ABM外的任一点O,确定在下列各条件下,
点P是否与A、B、M一定共面?课堂练习一例1. 如图,已知平行四边形ABCD,过平
面AC外一点O作射线OA、OB、OC、OD,在四条射线上分别取点E、F、G、H,并且使
求证:
四点E、F、G、H共面;
OBAHGFECD例1 (课本例)已知 ABCD ,从平面AC外一点O引向量 求证:四点E、F、G、H共面;证明:(﹡)代入所以 E、F、G、H共面。1.下列说明正确的是: (A)在平面内共线的向量在空间不一定共线
(B)在空间共线的向量在平面内不一定共线
(C)在平面内共线的向量在空间一定不共线
(D)在空间共线的向量在平面内一定共线2.下列说法正确的是: (A)平面内的任意两个向量都共线
(B)空间的任意三个向量都不共面
(C)空间的任意两个向量都共面
(D)空间的任意三个向量都共面课堂练习二B课堂练习二4.已知点M在平面ABC内,并且对空间任
意一点O, ,则x
的值为:D5.已知A、B、C三点不共线,对平面外一点
O,在下列条件下,点P是否与A、B、C共面?小结共面
