青岛版九年级上册第二章图形与变换测试(附答案)
文档属性
| 名称 | 青岛版九年级上册第二章图形与变换测试(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 173.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-24 00:00:00 | ||
图片预览

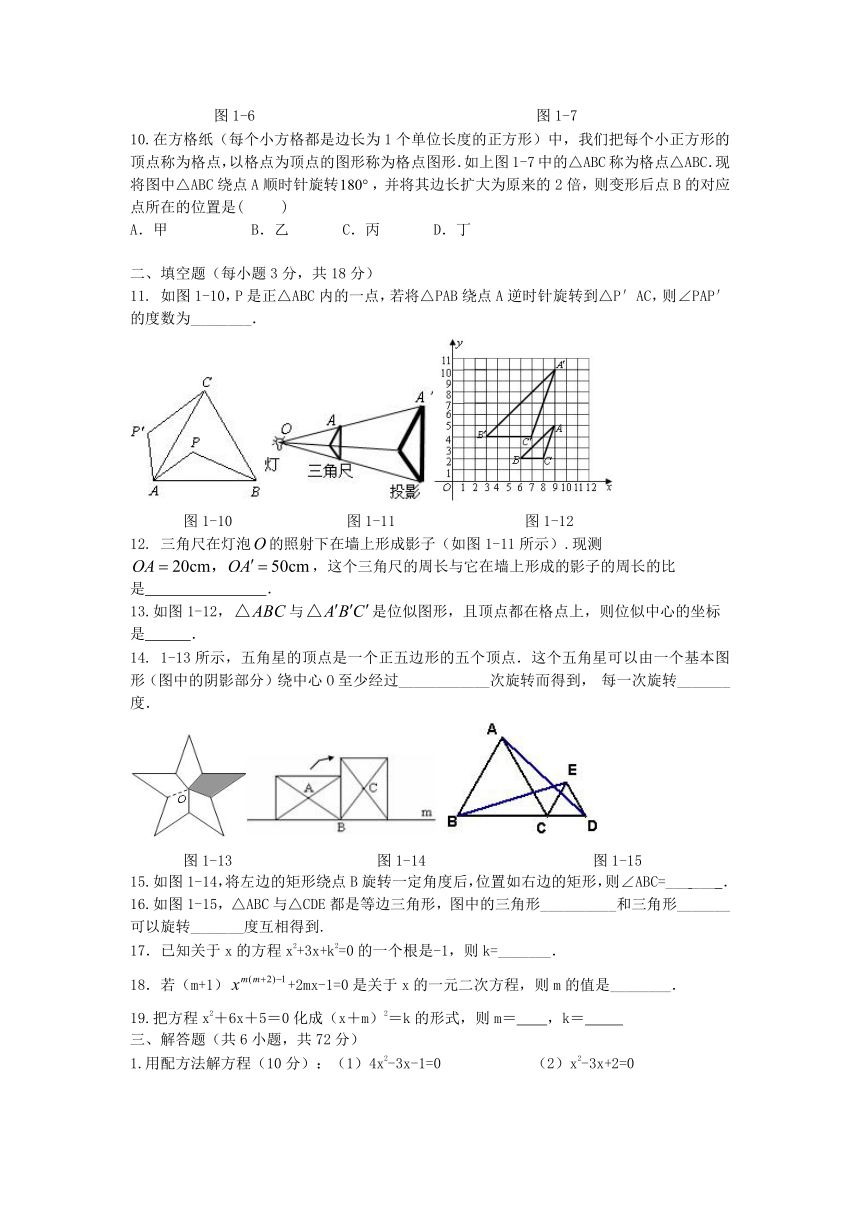
文档简介
初三数学测试题
(时间70分钟 满分100分)
一、选择题(每小题3分,共30分)
1. (2009广东广州)将图所示的图案通过平移后可以得到的图案是( )
2.如图1-2,有四个图案,它们绕中心旋转一定的角度后,都能和原来的图案相互重合,其中有一个图案与其余三个图案旋转的角度不同,它是( ).
图1-2 图1-3
3.如图1-3,△ABC按顺时针方向旋转一个角度后成为△A/B/C/,指出图中的旋转中心是 ( )
A.A点 B.B点 C.C点 D.B/点
4.下面关于x的方程中①ax2+bx+c=0;②3(x-9)2-(x+1)2=1;③x+3=;
④3x2+k =x-1.一元二次方程的个数是( )
A.1 B.2 C.3 D.4
5.若(x+y)(1-x-y)+6=0,则x+y的值是( )
A.2 B.3 C.-2或3 D.2或-3
6.请你先观察图,然后确定第四张图为( )
7.下面对于二次三项式-x2+4x-5的值的判断正确的是( )
A.恒大于0 B.恒小于0 C.不小于0 D.可能为0
8.用配方法解方程x2-2x-5 =0时,原方程应变形为 ( )
A (x+1)2=6 B (x-1)2=6
C (x+2)2=9 D (x-2)2=9
9. 如图1-6,将ΔPQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )
A. (-2,-4) B. (-2,4) C.(2,-3) D.(-1,-3)
图1-6 图1-7
10.在方格纸(每个小方格都是边长为1个单位长度的正方形)中,我们把每个小正方形的顶点称为格点,以格点为顶点的图形称为格点图形.如上图1-7中的△ABC称为格点△ABC.现将图中△ABC绕点A顺时针旋转,并将其边长扩大为原来的2倍,则变形后点B的对应点所在的位置是( )
A.甲 B.乙 C.丙 D.丁
二、填空题(每小题3分,共18分)
11. 如图1-10,P是正△ABC内的一点,若将△PAB绕点A逆时针旋转到△P′AC,则∠PAP′的度数为________.
图1-10 图1-11 图1-12
12. 三角尺在灯泡的照射下在墙上形成影子(如图1-11所示).现测,这个三角尺的周长与它在墙上形成的影子的周长的比是 .
13.如图1-12,与是位似图形,且顶点都在格点上,则位似中心的坐标是 .
14. 1-13所示,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心O至少经过____________次旋转而得到, 每一次旋转_______度.
图1-13 图1-14 图1-15
15.如图1-14,将左边的矩形绕点B旋转一定角度后,位置如右边的矩形,则∠ABC=___ ___ .
16.如图1-15,△ABC与△CDE都是等边三角形,图中的三角形__________和三角形_______可以旋转_______度互相得到.
17.已知关于x的方程x2+3x+k2=0的一个根是-1,则k=_______.
18.若(m+1)+2mx-1=0是关于x的一元二次方程,则m的值是________.
19.把方程x2+6x+5=0化成(x+m)2=k的形式,则m= ,k=
三、解答题(共6小题,共72分)
1.用配方法解方程(10分):(1)4x2-3x-1=0 (2)x2-3x+2=0
2.如图1-16是由若干个边长为1的小正方形组成的网格,请在图中作出将“蘑菇”ABCDE绕A点逆时针旋转90(再向右平移2个单位的图形(其中C、D为所在小正方形边的中点).(5分)
图1-16
4.如图1-20,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE的旋转图形.(9分)(1)旋转中心是哪一点?(2分)(2)旋转了多少度?(2分)(3)AF的长度是多少?(2分)
(4)如果连结EF,那么△AEF是怎样的三角形?(3分)
图1-20
5.1.若点A的坐标是(a,b)且a、b满足+b2+4b+4=0,求点A绕原点O逆时针旋转90°的对应点A′的坐标.(7分)
6.在中,将绕点顺时针旋转角得交于点,分别交于两点.(12分)
(1)如图1-21的图1,观察并猜想,在旋转过程中,线段与有怎样的数量关系?并证明你的结论;(4分)
图1-21
(2)如图1-21的图2,当时,试判断四边形的形状,并说明理由;(4分)
(3)在(2)的情况下,求的长.(4分)
第二章 图形与变换单元检测答案
一、1.A 2.A 3.A 4.A 5.B 6.A 7.A 8.C 9.B 10.D
二、11.60° 12. 13.(9,0) 14.4,72 15.90o 16.点O,∠MON,90
三、17.解:如图,
18.解:(1)点C;(2)∠BCB′或∠ACA′;(3)点M转到了B′C的中点位置上;
19.解:将△ABQ绕点A逆时针旋转90°,得到△ADE,由旋转的性质可得∠E=∠AQB,∠EAD=∠QAB.
又因为∠PAE=90°-∠PAQ=90°-∠BAQ=∠DAQ=∠AQB=∠E.
在△PAE中,得到AP=PE=DP+DE=DP+BQ.
20.解:∵四边形ABCD、四边形AKLM是正方形
∴AB=AD,AK=AM,且∠BAD=∠KAM为旋转角且为90°
∴△ADM是以A为旋转中心,∠BAD为旋转角由△ABK旋转而成的, ∴BK=DM
21.解:(1)旋转中心是A点.
(2)∵△ABF是由△ADE旋转而成的
∴B是D的对应点 ∴∠DAB=90°就是旋转角
(3)∵AD=1,DE= ∴AE==
∵对应点到旋转中心的距离相等且F是E的对应点 ∴AF=
(4)∵∠EAF=90°(与旋转角相等)且AF=AE ∴△EAF是等腰直角三角形.
22.解:(1)
证明:(证法一)
由旋转可知,
∴
∴又
∴即
(证法二)
由旋转可知,而
∴∴∴即
(2)四边形是菱形.
证明:同理
∴四边形是平行四边形. 又∴四边形是菱形.
(3)(解法一)过点作于点,则
在中,
由(2)知四边形是菱形,
∴
∴
(解法二)∴
在中,
∴
(时间70分钟 满分100分)
一、选择题(每小题3分,共30分)
1. (2009广东广州)将图所示的图案通过平移后可以得到的图案是( )
2.如图1-2,有四个图案,它们绕中心旋转一定的角度后,都能和原来的图案相互重合,其中有一个图案与其余三个图案旋转的角度不同,它是( ).
图1-2 图1-3
3.如图1-3,△ABC按顺时针方向旋转一个角度后成为△A/B/C/,指出图中的旋转中心是 ( )
A.A点 B.B点 C.C点 D.B/点
4.下面关于x的方程中①ax2+bx+c=0;②3(x-9)2-(x+1)2=1;③x+3=;
④3x2+k =x-1.一元二次方程的个数是( )
A.1 B.2 C.3 D.4
5.若(x+y)(1-x-y)+6=0,则x+y的值是( )
A.2 B.3 C.-2或3 D.2或-3
6.请你先观察图,然后确定第四张图为( )
7.下面对于二次三项式-x2+4x-5的值的判断正确的是( )
A.恒大于0 B.恒小于0 C.不小于0 D.可能为0
8.用配方法解方程x2-2x-5 =0时,原方程应变形为 ( )
A (x+1)2=6 B (x-1)2=6
C (x+2)2=9 D (x-2)2=9
9. 如图1-6,将ΔPQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )
A. (-2,-4) B. (-2,4) C.(2,-3) D.(-1,-3)
图1-6 图1-7
10.在方格纸(每个小方格都是边长为1个单位长度的正方形)中,我们把每个小正方形的顶点称为格点,以格点为顶点的图形称为格点图形.如上图1-7中的△ABC称为格点△ABC.现将图中△ABC绕点A顺时针旋转,并将其边长扩大为原来的2倍,则变形后点B的对应点所在的位置是( )
A.甲 B.乙 C.丙 D.丁
二、填空题(每小题3分,共18分)
11. 如图1-10,P是正△ABC内的一点,若将△PAB绕点A逆时针旋转到△P′AC,则∠PAP′的度数为________.
图1-10 图1-11 图1-12
12. 三角尺在灯泡的照射下在墙上形成影子(如图1-11所示).现测,这个三角尺的周长与它在墙上形成的影子的周长的比是 .
13.如图1-12,与是位似图形,且顶点都在格点上,则位似中心的坐标是 .
14. 1-13所示,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心O至少经过____________次旋转而得到, 每一次旋转_______度.
图1-13 图1-14 图1-15
15.如图1-14,将左边的矩形绕点B旋转一定角度后,位置如右边的矩形,则∠ABC=___ ___ .
16.如图1-15,△ABC与△CDE都是等边三角形,图中的三角形__________和三角形_______可以旋转_______度互相得到.
17.已知关于x的方程x2+3x+k2=0的一个根是-1,则k=_______.
18.若(m+1)+2mx-1=0是关于x的一元二次方程,则m的值是________.
19.把方程x2+6x+5=0化成(x+m)2=k的形式,则m= ,k=
三、解答题(共6小题,共72分)
1.用配方法解方程(10分):(1)4x2-3x-1=0 (2)x2-3x+2=0
2.如图1-16是由若干个边长为1的小正方形组成的网格,请在图中作出将“蘑菇”ABCDE绕A点逆时针旋转90(再向右平移2个单位的图形(其中C、D为所在小正方形边的中点).(5分)
图1-16
4.如图1-20,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE的旋转图形.(9分)(1)旋转中心是哪一点?(2分)(2)旋转了多少度?(2分)(3)AF的长度是多少?(2分)
(4)如果连结EF,那么△AEF是怎样的三角形?(3分)
图1-20
5.1.若点A的坐标是(a,b)且a、b满足+b2+4b+4=0,求点A绕原点O逆时针旋转90°的对应点A′的坐标.(7分)
6.在中,将绕点顺时针旋转角得交于点,分别交于两点.(12分)
(1)如图1-21的图1,观察并猜想,在旋转过程中,线段与有怎样的数量关系?并证明你的结论;(4分)
图1-21
(2)如图1-21的图2,当时,试判断四边形的形状,并说明理由;(4分)
(3)在(2)的情况下,求的长.(4分)
第二章 图形与变换单元检测答案
一、1.A 2.A 3.A 4.A 5.B 6.A 7.A 8.C 9.B 10.D
二、11.60° 12. 13.(9,0) 14.4,72 15.90o 16.点O,∠MON,90
三、17.解:如图,
18.解:(1)点C;(2)∠BCB′或∠ACA′;(3)点M转到了B′C的中点位置上;
19.解:将△ABQ绕点A逆时针旋转90°,得到△ADE,由旋转的性质可得∠E=∠AQB,∠EAD=∠QAB.
又因为∠PAE=90°-∠PAQ=90°-∠BAQ=∠DAQ=∠AQB=∠E.
在△PAE中,得到AP=PE=DP+DE=DP+BQ.
20.解:∵四边形ABCD、四边形AKLM是正方形
∴AB=AD,AK=AM,且∠BAD=∠KAM为旋转角且为90°
∴△ADM是以A为旋转中心,∠BAD为旋转角由△ABK旋转而成的, ∴BK=DM
21.解:(1)旋转中心是A点.
(2)∵△ABF是由△ADE旋转而成的
∴B是D的对应点 ∴∠DAB=90°就是旋转角
(3)∵AD=1,DE= ∴AE==
∵对应点到旋转中心的距离相等且F是E的对应点 ∴AF=
(4)∵∠EAF=90°(与旋转角相等)且AF=AE ∴△EAF是等腰直角三角形.
22.解:(1)
证明:(证法一)
由旋转可知,
∴
∴又
∴即
(证法二)
由旋转可知,而
∴∴∴即
(2)四边形是菱形.
证明:同理
∴四边形是平行四边形. 又∴四边形是菱形.
(3)(解法一)过点作于点,则
在中,
由(2)知四边形是菱形,
∴
∴
(解法二)∴
在中,
∴
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
