2021-2022学年北师大版九年级数学下册1.2第2课时二次函数y=ax2,y=ax2+c的图象和性质练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册1.2第2课时二次函数y=ax2,y=ax2+c的图象和性质练习题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 131.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 08:33:09 | ||
图片预览


文档简介
第2课时 二次函数y=ax2,y=ax2+c的图象和性质
【基础练习】
知识点1 二次函数y=ax2的图象和性质
1.抛物线y=ax2(a>0)一定经过 ( )
A.第一、二象限 B.第三、四象限
C.第一、三象限 D.第二、四象限
2.在同一平面直角坐标系中,抛物线y=-4x2,y=x2,y=-x2的共同特点是 ( )
A.关于y轴对称,开口向下
B.关于x轴对称,形状相同
C.当x<0时,y随x的增大而增大
D.顶点都是原点
3.若原点是抛物线y=(m+1)x2的最高点,则m的取值范围是 ( )
A.m<0 B.m<1
C.m<-1 D.m>-1
4.已知抛物线y=ax2(a>0)过A(-2,y1),B(1,y2)两点,则下列关系式一定正确的是 ( )
A.y1>0>y2 B.y2>0>y1
C.y1>y2>0 D.y2>y1>0
5.如图4所示,四个二次函数的图象对应的表达式分别是①y=ax2;②y=bx2;③y=cx2;④y=dx2,则a,b,c,d的大小关系为 .(用“>”连接)
图4
6.若抛物线y=ax2与抛物线y=2x2关于x轴对称,则a= .
知识点2 二次函数y=ax2+c的图象和性质
7.二次函数y=x2-2的图象的顶点坐标为 ( )
A.(0,0) B.(0,-2)
C.(-,-2) D.(-,2)
8.二次函数y=-x2-1的图象大致是 ( )
图5
9.下列关于二次函数y=x2-3的图象与性质的描述,不正确的是 ( )
A.该函数图象的开口向上
B.函数值y随自变量x的值的增大而增大
C.抛物线的对称轴是直线x=0
D.抛物线与x轴有两个交点
10.如果抛物线y=(k-1)x2+9在y轴左侧的部分是上升的,那么k的取值范围是 .
知识点3 图象的平移
11.将抛物线y=2x2向下平移3个单位长度,得到的抛物线的表达式为 ( )
A.y=2x2+3 B.y=2x2-3
C.y=2(x+3)2 D.y=2(x-3)2
12.[教材习题2.3第3题变式题]要得到抛物线y=x2-4,可将抛物线y=x2+2 ( )
A.向上平移2个单位长度
B.向下平移2个单位长度
C.向上平移6个单位长度
D.向下平移6个单位长度
13.把二次函数y=-x2的图象向上平移2个单位长度.
(1)求新图象的表达式、顶点坐标和对称轴;
(2)画出平移后的函数图象;
(3)求平移后的函数的最大值或最小值,并求对应的x值.
图6
【综合练习】
14.二次函数y=ax2与一次函数y=ax+a在同一直角坐标系中的大致图象可能是图7中的( )
图7
15.已知二次函数y=ax2+c,当x取x1,x2(x1≠x2)时,函数值相等,则当x取x1+x2时,函数值为( )
A.a+c B.a-c C.-c D.c
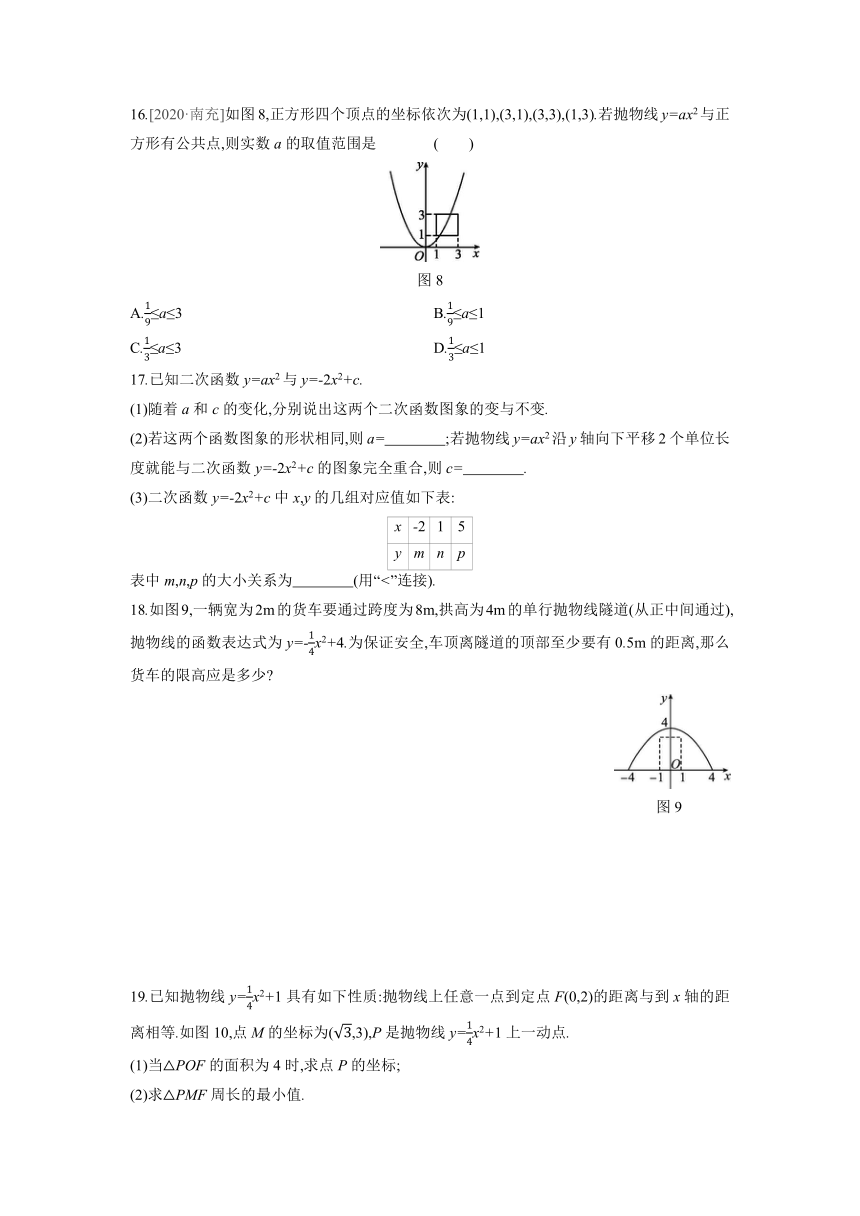
16.[2020·南充]如图8,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3).若抛物线y=ax2与正方形有公共点,则实数a的取值范围是 ( )
图8
A.≤a≤3 B.≤a≤1
C.≤a≤3 D.≤a≤1
17.已知二次函数y=ax2与y=-2x2+c.
(1)随着a和c的变化,分别说出这两个二次函数图象的变与不变.
(2)若这两个函数图象的形状相同,则a= ;若抛物线y=ax2沿y轴向下平移2个单位长度就能与二次函数y=-2x2+c的图象完全重合,则c= .
(3)二次函数y=-2x2+c中x,y的几组对应值如下表:
x -2 1 5
y m n p
表中m,n,p的大小关系为 (用“<”连接).
18.如图9,一辆宽为2m的货车要通过跨度为8m,拱高为4m的单行抛物线隧道(从正中间通过),抛物线的函数表达式为y=-x2+4.为保证安全,车顶离隧道的顶部至少要有0.5m的距离,那么货车的限高应是多少
图9
19.已知抛物线y=x2+1具有如下性质:抛物线上任意一点到定点F(0,2)的距离与到x轴的距离相等.如图10,点M的坐标为(,3),P是抛物线y=x2+1上一动点.
(1)当△POF的面积为4时,求点P的坐标;
(2)求△PMF周长的最小值.
图10
答案
1.A 2.D
3.C [解析]∵原点是抛物线y=(m+1)x2的最高点,∴m+1<0,即m<-1.故选C.
4.C [解析]把A(-2,y1),B(1,y2)分别代入y=ax2,得y1=4a,y2=a.因为a>0,所以4a>a>0,即y1>y2>0.故选C.
5.a>b>d>c 6.-2
7.B 8.B 9.B
10.k<1
11.B 12.D
13.解:(1)新图象的表达式是y=-x2+2,顶点坐标是(0,2),对称轴是y轴.
(2)略.
(3)平移后的函数的最大值为2,对应的x值为0.
14.D [解析]由一次函数y=ax+a可知,一次函数的图象与x轴交于点(-1,0),排除A,B;
当a>0时,二次函数的图象开口向上,一次函数的图象经过第一、二、三象限;当a<0时,二次函数的图象开口向下,一次函数的图象经过第二、三、四象限,排除C.故选D.
15.D [解析]因为二次函数y=ax2+c的图象的对称轴是直线x=0,当x取x1,x2(x1≠x2)时,函数值相等,所以x1=-x2,即x1+x2=0.把x=0代入y=ax2+c,得y=c.
16.A
17.解:(1)二次函数y=ax2的图象随着a的变化,开口大小和开口方向都会变化,但是对称轴、顶点坐标不会改变;二次函数y=-2x2+c的图象随着c的变化,开口大小和开口方向都没有改变,对称轴也没有改变,但是,顶点坐标会发生改变.
(2)函数y=ax2与y=-2x2+c的图象形状相同,则a=±2.因为抛物线y=ax2沿y轴向下平移2个单位长度得到y=ax2-2,与二次函数y=-2x2+c的图象完全重合,则c=-2.故答案为±2,-2.
(3)由函数y=-2x2+c可知,抛物线开口向下,对称轴为y轴.因为1-0<0-(-2)<5-0,则p18.解:∵抛物线的函数表达式为y=-x2+4,宽为2m的货车从正中间通过,
∴当x=1时,y=-×12+4=.
又∵车顶离隧道的顶部至少要有0.5m的距离,∴限高为-0.5=3.25(m).
即货车的限高应是3.25m.
19.解:(1)设点P的坐标为x,x2+1.
∵点F的坐标为(0,2),
∴OF=2,
∴当△POF的面积为4时,×2×|x|=4,
解得x=±4,
∴x2+1=×(±4)2+1=5,
∴点P的坐标为(-4,5)或(4,5).
(2)如图,过点M作ME⊥x轴于点E,交抛物线y=x2+1于点P,此时△PMF的周长最小.
由题意,得PF=PE.
∵F(0,2),M(,3),
∴ME=3,FM==2,
∴△PMF周长的最小值=FM+PM+PF=FM+PM+PE=FM+ME=2+3=5.
【基础练习】
知识点1 二次函数y=ax2的图象和性质
1.抛物线y=ax2(a>0)一定经过 ( )
A.第一、二象限 B.第三、四象限
C.第一、三象限 D.第二、四象限
2.在同一平面直角坐标系中,抛物线y=-4x2,y=x2,y=-x2的共同特点是 ( )
A.关于y轴对称,开口向下
B.关于x轴对称,形状相同
C.当x<0时,y随x的增大而增大
D.顶点都是原点
3.若原点是抛物线y=(m+1)x2的最高点,则m的取值范围是 ( )
A.m<0 B.m<1
C.m<-1 D.m>-1
4.已知抛物线y=ax2(a>0)过A(-2,y1),B(1,y2)两点,则下列关系式一定正确的是 ( )
A.y1>0>y2 B.y2>0>y1
C.y1>y2>0 D.y2>y1>0
5.如图4所示,四个二次函数的图象对应的表达式分别是①y=ax2;②y=bx2;③y=cx2;④y=dx2,则a,b,c,d的大小关系为 .(用“>”连接)
图4
6.若抛物线y=ax2与抛物线y=2x2关于x轴对称,则a= .
知识点2 二次函数y=ax2+c的图象和性质
7.二次函数y=x2-2的图象的顶点坐标为 ( )
A.(0,0) B.(0,-2)
C.(-,-2) D.(-,2)
8.二次函数y=-x2-1的图象大致是 ( )
图5
9.下列关于二次函数y=x2-3的图象与性质的描述,不正确的是 ( )
A.该函数图象的开口向上
B.函数值y随自变量x的值的增大而增大
C.抛物线的对称轴是直线x=0
D.抛物线与x轴有两个交点
10.如果抛物线y=(k-1)x2+9在y轴左侧的部分是上升的,那么k的取值范围是 .
知识点3 图象的平移
11.将抛物线y=2x2向下平移3个单位长度,得到的抛物线的表达式为 ( )
A.y=2x2+3 B.y=2x2-3
C.y=2(x+3)2 D.y=2(x-3)2
12.[教材习题2.3第3题变式题]要得到抛物线y=x2-4,可将抛物线y=x2+2 ( )
A.向上平移2个单位长度
B.向下平移2个单位长度
C.向上平移6个单位长度
D.向下平移6个单位长度
13.把二次函数y=-x2的图象向上平移2个单位长度.
(1)求新图象的表达式、顶点坐标和对称轴;
(2)画出平移后的函数图象;
(3)求平移后的函数的最大值或最小值,并求对应的x值.
图6
【综合练习】
14.二次函数y=ax2与一次函数y=ax+a在同一直角坐标系中的大致图象可能是图7中的( )
图7
15.已知二次函数y=ax2+c,当x取x1,x2(x1≠x2)时,函数值相等,则当x取x1+x2时,函数值为( )
A.a+c B.a-c C.-c D.c
16.[2020·南充]如图8,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3).若抛物线y=ax2与正方形有公共点,则实数a的取值范围是 ( )
图8
A.≤a≤3 B.≤a≤1
C.≤a≤3 D.≤a≤1
17.已知二次函数y=ax2与y=-2x2+c.
(1)随着a和c的变化,分别说出这两个二次函数图象的变与不变.
(2)若这两个函数图象的形状相同,则a= ;若抛物线y=ax2沿y轴向下平移2个单位长度就能与二次函数y=-2x2+c的图象完全重合,则c= .
(3)二次函数y=-2x2+c中x,y的几组对应值如下表:
x -2 1 5
y m n p
表中m,n,p的大小关系为 (用“<”连接).
18.如图9,一辆宽为2m的货车要通过跨度为8m,拱高为4m的单行抛物线隧道(从正中间通过),抛物线的函数表达式为y=-x2+4.为保证安全,车顶离隧道的顶部至少要有0.5m的距离,那么货车的限高应是多少
图9
19.已知抛物线y=x2+1具有如下性质:抛物线上任意一点到定点F(0,2)的距离与到x轴的距离相等.如图10,点M的坐标为(,3),P是抛物线y=x2+1上一动点.
(1)当△POF的面积为4时,求点P的坐标;
(2)求△PMF周长的最小值.
图10
答案
1.A 2.D
3.C [解析]∵原点是抛物线y=(m+1)x2的最高点,∴m+1<0,即m<-1.故选C.
4.C [解析]把A(-2,y1),B(1,y2)分别代入y=ax2,得y1=4a,y2=a.因为a>0,所以4a>a>0,即y1>y2>0.故选C.
5.a>b>d>c 6.-2
7.B 8.B 9.B
10.k<1
11.B 12.D
13.解:(1)新图象的表达式是y=-x2+2,顶点坐标是(0,2),对称轴是y轴.
(2)略.
(3)平移后的函数的最大值为2,对应的x值为0.
14.D [解析]由一次函数y=ax+a可知,一次函数的图象与x轴交于点(-1,0),排除A,B;
当a>0时,二次函数的图象开口向上,一次函数的图象经过第一、二、三象限;当a<0时,二次函数的图象开口向下,一次函数的图象经过第二、三、四象限,排除C.故选D.
15.D [解析]因为二次函数y=ax2+c的图象的对称轴是直线x=0,当x取x1,x2(x1≠x2)时,函数值相等,所以x1=-x2,即x1+x2=0.把x=0代入y=ax2+c,得y=c.
16.A
17.解:(1)二次函数y=ax2的图象随着a的变化,开口大小和开口方向都会变化,但是对称轴、顶点坐标不会改变;二次函数y=-2x2+c的图象随着c的变化,开口大小和开口方向都没有改变,对称轴也没有改变,但是,顶点坐标会发生改变.
(2)函数y=ax2与y=-2x2+c的图象形状相同,则a=±2.因为抛物线y=ax2沿y轴向下平移2个单位长度得到y=ax2-2,与二次函数y=-2x2+c的图象完全重合,则c=-2.故答案为±2,-2.
(3)由函数y=-2x2+c可知,抛物线开口向下,对称轴为y轴.因为1-0<0-(-2)<5-0,则p
∴当x=1时,y=-×12+4=.
又∵车顶离隧道的顶部至少要有0.5m的距离,∴限高为-0.5=3.25(m).
即货车的限高应是3.25m.
19.解:(1)设点P的坐标为x,x2+1.
∵点F的坐标为(0,2),
∴OF=2,
∴当△POF的面积为4时,×2×|x|=4,
解得x=±4,
∴x2+1=×(±4)2+1=5,
∴点P的坐标为(-4,5)或(4,5).
(2)如图,过点M作ME⊥x轴于点E,交抛物线y=x2+1于点P,此时△PMF的周长最小.
由题意,得PF=PE.
∵F(0,2),M(,3),
∴ME=3,FM==2,
∴△PMF周长的最小值=FM+PM+PF=FM+PM+PE=FM+ME=2+3=5.
