3.1.1-3.1.2 随机事件的概率和意义-2021-2022学年数学人教A版必修3同步 课件(共45张PPT)
文档属性
| 名称 | 3.1.1-3.1.2 随机事件的概率和意义-2021-2022学年数学人教A版必修3同步 课件(共45张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 10:35:22 | ||
图片预览










文档简介
(共45张PPT)
3.1.1 随机事件的概率
*
*
财富梦想调查
你有买彩票的经历吗?
买之前你确定能中奖吗?
你意识到买彩票中大奖的机会有多大吗?
七星彩:国家体育总局发行的全国型彩票,共7位数,每一位数均来自0~9这十个数字,那么中一等奖(500万)的概率是多少?
双色球:中国福利彩票中心发行的全国型彩票,从1~33里选出6个数组成六个红球,从1~16里选出1个数构成一个蓝球,这就是双色球,那么中一等奖(500万)的概率是多少?
概率论的诞生,虽然渊源于靠碰运气取胜的游戏,但在今天,却已成为人类知识最重要的一部分.
—— 拉普拉斯(法国数学家)
*
*
下列事件发生与否,各有什么特点呢?
(1)“地球不停地转动”
(2)“木柴燃烧,产生能量”
(3)“在常温下,石头在一天内风化”
(4)“某人投球,三分!”
(5)“掷一枚硬币,出现正面”
(6)“在标准大气压下且温度低于0℃时,雪融化”
必然发生
必然发生
不可能发生
不可能发生
可能发生也可能不发生
可能发生也可能不发生
*
*
定义:
随机事件:
在一定条件下可能发生也可能不发生的事件叫随机事件。
必然事件:
在一定条件下必然要发生的事件叫必然事件。
不可能事件:
在一定条件下不可能发生的事件叫不可能事件。
确定事件和随机事件统称为事件,一般用大写字母A,B,C…表示。
*
*
这些事件发生与否,各有什么特点呢?
(1)“地球不停地转动”
(2)“木柴燃烧,产生能量”
(3)“在常温下,石头在一天内风化”
(4)“某人投球,三分!”
(5)“掷一枚硬币,出现正面”
(6)“在标准大气压下且温度低于0℃时,雪融化”
必然发生
必然发生
不可能发生
不可能发生
可能发生也可能不发生
可能发生也可能不发生
必然事件
必然事件
不可能事件
随机事件
随机事件
不可能事件
*
*
随机事件是在一定条件下可能发生 也可能不发生的事件。
对于随机事件,知道它发生的可能性大小是非常重要的
我们用概率度量随机事件发生的可能性大小。随机事件发生的可能性大则随机事件发生的
概率大;概率小则随机事件发生的可能性小。
我们如何获得随机事件发生的概率?
要了解随机事件发生的可能性大小,最直接的方法就是试验。
*
*
在相同的条件S下重复n次试验,若某一事件A出现的次数为nA,
则称nA为事件A出现的频数,
那么事件A出现的频率fn(A)等于什么?
频率的取值范围是什么?
*
*
让我们来做一个试验:
投掷一枚硬币,出现正面可能性有多大?
*
*
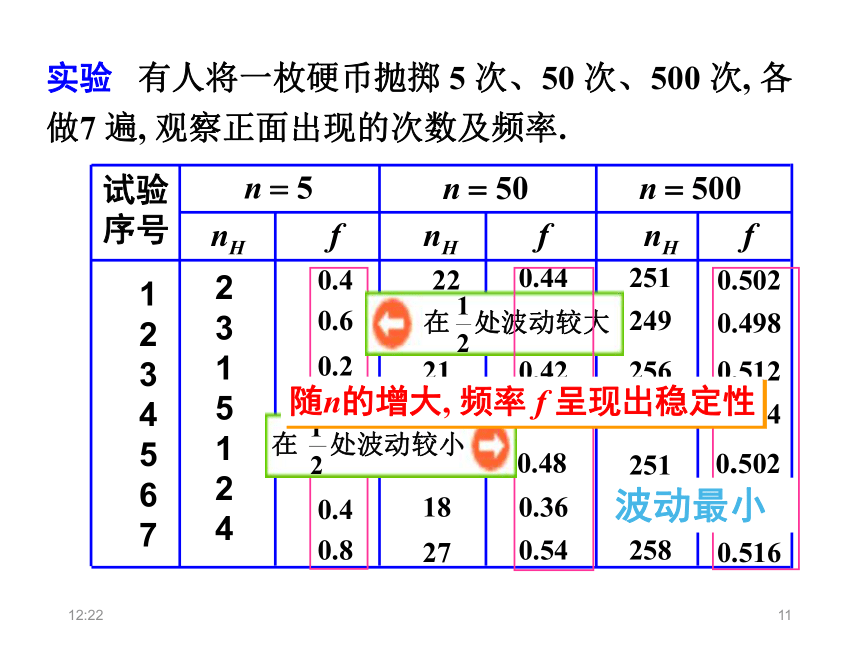
实验 有人将一枚硬币抛掷 5 次、50 次、500 次, 各做7 遍, 观察正面出现的次数及频率.
试验
序号
22
25
21
25
24
18
27
251
249
256
247
251
262
258
0.4
0.6
0.2
1.0
0.2
0.4
0.8
0.44
0.50
0.42
0.48
0.36
0.54
0.502
0.498
0.512
0.494
0.524
0.516
0.50
0.502
波动最小
随n的增大, 频率 f 呈现出稳定性
1
2
3
4
5
6
7
2
3
1
5
1
2
4
*
*
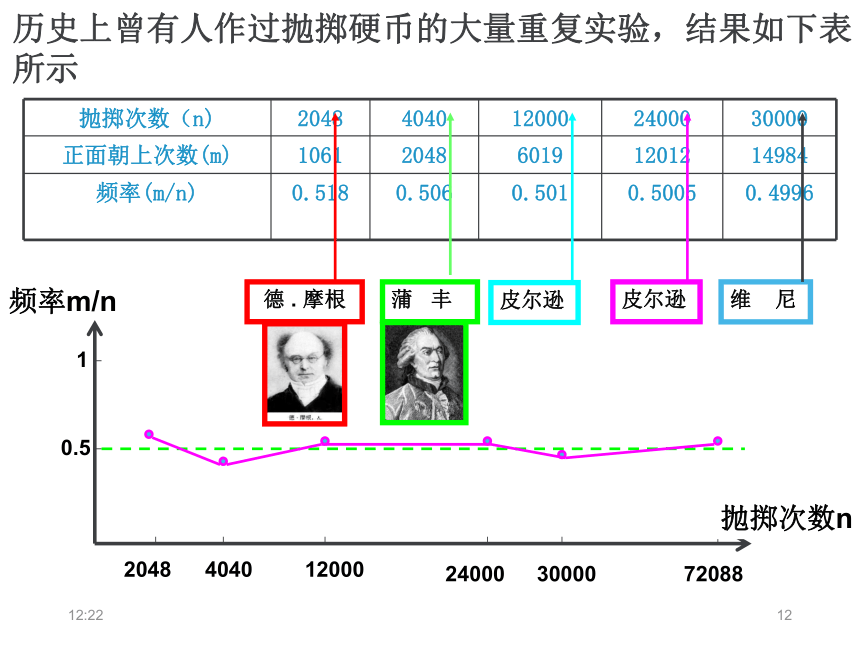
抛掷次数(n) 2048 4040 12000 24000 30000
正面朝上次数(m) 1061 2048 6019 12012 14984
频率(m/n) 0.518 0.506 0.501 0.5005 0.4996
历史上曾有人作过抛掷硬币的大量重复实验,结果如下表所示
抛掷次数n
频率m/n
0.5
1
2048
4040
12000
24000
30000
72088
德 . 摩根
蒲 丰
皮尔逊
皮尔逊
维 尼
*
*
实验中只出现两种结果,没有其它结果,每一次试验的结果不固定,但只是“正面”、“反面”两种中的一种,且它们出现的频率均接近于0.5,但不相等。
(1)在每次实验中可能出现几种实验结果?还有其它实验结果吗?
根据实验分别回答下列问题:
(2)如果同学们再重复一次上面的试验,汇总结果还会和这次汇总结果一致吗
*
*
在大量重复实验后,随着次数的增加,频率会逐渐稳定在区间[0,1]中的某个常数上。
(3)如果允许你做大量重复试验,你认为结果又如何呢?
根据实验分别回答下列问题:
总结:“掷一枚硬币,正面朝上”在一次试验中是否发生不能确定,但随着试验次数的增加,正面朝上的频率逐渐地接近于0.5.
*
*
概率:
经过大量的重复试验,事件A发生的频率会逐渐稳定在区间[0,1]中的某个常数上.
用频率fn(A)来估计概率P(A)
是一个确定的值
试 验 结 论:
这个常数就是事件A发生的概率.
随着试验次数的增加,频率稳定在0.5附近
*
*
一般地,在大量重复进行同一试验时,事件A发生的频率 总是接近于某个常数,在它附近摆动。这个常数叫做事件A的概率,记作P(A)。
通过实验,我们可以发觉:
事件A的概率:
注:
事件A的概率:
(1)频率m/n总在P(A)附近摆动,当n越大时,摆动幅度越小。
(2)0≤P(A)≤1 不可能事件的概率为0,必然事件为1,随机事件的概率大于0而小于1。
(3)大量重复进行同一试验时,随机事件及其概率呈现出规律性。
*
*
☆频率与概率的区别:
1. 事件A发生的频率fn(A)是(不变,变化)的;
事件A发生的概率P(A)是(不变,变化)的;
概率是一个确定的常数,是客观存在的,与每次试验结果无关,与试验次数无关,甚至与做不做试验无关.
2.随着试验次数的增加频率稳定于概率;
3.概率是频率的稳定值,频率是概率的近似值;
因此在实际中我们求一个事件的概率时,有时通过进行大量的重复试验,用这个事件发生的频率近似地作为它的概率.
*
*
概率是频率的稳定值,而频率是概率的近似值。
概率反映了随机事件发生的可能性的大小。
频率与概率的关系
总之:
*
*
1.下列说法正确的是( )
A.任一事件的概率总在(0.1)内
B.不可能事件的概率不一定为0
C.必然事件的概率一定为1
D.以上均不对
解析:必然事件的概率为1,不可能事件的概率为0,随机事件的概率在0到1之间.
故选C.
3.1.2 概率的意义
人生必须去搏,敢于冒风险,对随机事件作出自己的判断,把“不一定”的事情变成现实,这才是“胜利”。
*
*
1.概率的正确理解
1.有人说,既然抛掷一枚硬币出现正面 的概率为0.5,那么连续两次抛掷一枚质地均匀的硬币,一定是一次正面朝上,一次反面朝上。 你认为这种想法正确吗?
2.有人说,中奖率为1/1000的彩票,买1000张一定中奖,这种理解对吗?
*
*
1.概率的正确理解:
有人说,既然抛掷一枚硬币出现正面的概率为0.5,那么连续两次抛掷一枚质地均匀的硬币,一定是一次正面朝上,一次反面朝上,你认为这种想法正确吗
点评:这种想法是错误的.因为连续两次抛掷一枚质地均匀的硬币仅仅是做两次重复的试验,试验的结果仍然是随机的,当然可以两次均出现正面朝上或两次均出现反面朝上.
*
*
点评:不一定.因为每张彩票是否中奖是随机的,1000张彩票有几张中奖也是随机的.这就是说,每张彩票既可能中奖也可能不中奖,因此1000张彩票中可能没有一张中奖,也可能有一张、两张乃至多张中奖.
虽然中奖张数是随机的,但这种随机性中具有规律性.即随着所买彩票张数的增加,其中中奖彩票所占的比例可能越接近于1/1000.
1.概率的正确理解:
有人说,中奖率为1/1000的彩票,买1000张一定中奖,这种理解对吗?
*
*
例如:把同样大小的9个白色乒乓球和1个黄色乒乓球放在一个不透明的袋子中,每次摸出1球后放回袋中,这样摸10次,
(1)每次摸到白球的可能性大还是黄球的可能性大
(2)摸的10次中是否一定至少有1次摸到黄球
点评:每次摸到白球的概率是0.9,而每次摸到黄球的概率为0.1,因此每次摸到白球的可能性要大.
尽管每次摸到黄球的概率为0.1,但摸10次球,不一定能摸到黄球.
*
*
归纳小结:
随机事件在一次试验中发生与否是随机的,但随机中含有规律性.认识了这种随机性中的规律性,就能使我们比较准确地预测随机事件发生的可能性.
*
*
2、游戏的公平性
观察:你有没有注意到在乒乓球、排球等体育比赛前,裁判是如何确定发球权的?你觉得对比赛双方公平吗?
判断发球权的常用方法:裁判员拿出一个抽签器,它是一个像大硬币似的均匀塑料圆板,一面是红圈,一面是绿圈,然后随意指定一名运动员,要他猜上抛的抽签器落到球台上时,是红圈那面朝上还是绿圈那面朝上.如果他猜对了,就由他先发球,否则,由另一方先发球.
*
*
2.游戏的公平性
分析:因为抽签器上抛后,红圈朝上与绿圈朝上的概率都是0.5,因此任何一名运动员猜中的概率都是0.5,也就是每个运动员取得发球权的概率均为0.5,所以这个规则是公平的.
*
*
这样的游戏公平吗
小军和小民玩掷骰子是游戏,他们约定:两颗骰子掷出去,如果朝上的两个数的和是5,那么小军获胜,如果朝上的两个数的和是7,那么小民获胜.这样的游戏公平吗?
事件:掷双骰子
A:朝上两个数的和是5
B:朝上两个数的和是7
关键是比较A发生的可能性和B发
生的可能性的大小.
*
*
1点 2点 3点 4点 5点 6点
1点 2 3 4 5 6 7
2点 3 4 5 6 7 8
3点 4 5 6 7 8 9
4点 5 6 7 8 9 10
5点 6 7 8 9 10 11
6点 7 8 9 10 11 12
观察表中数据,可发现,做同时掷两枚硬币的试验时,事件A发生的可能性(4种情况)比事件B发生的可能性(6种情况)小,即P(A)*
*
3.决策中的概率思想:
〖思考〗连续掷硬币1000次,结果1000次全部是正面朝上,出现这样的结果,你会怎样想
〖思考〗如果一个袋中有99个红球,1个白球,或者有99个白球,1个红球,事先不知道到底是哪种情况.一个人从袋中随机摸出1球,结果发现是红球,你认为这个袋中是有99个红球,1个白球,还是有99个白球,1个红球呢
*
*
如果我们面临的是从多个可选答案中挑选正确答案的决策任务,那么“使得样本出现的可能性最大”可以作为决策的准则,这种判断问题的方法称为极大似然法。
极大似然法是统计中重要的统计思想方法之一。
*
*
1.设某厂产品的次品率为2%,估算该厂8000件产品中合格品的件数可能为()
A.160件 B.7840件 C.7998件 D.7800件
*
*
4.天气预报的概率解释
〖思考〗某地气象局预报说,明天本地降水概率为70%,你认为下面两个解释中哪一个代表气象局的观点
(1)明天本地有70%的区域下雨,30%的区域不下雨;
(2)明天本地下雨的机会是70%.
√
*
*
例:生活中,我们经常听到这样的议论:“天气预报说昨天降水概率为90%,结果根本一点雨都没下,天气预报也太不准确了。”这样的说法对吗,你能给出解释吗?
解:天气预报的“降水”是一个随机事件,概率为90%指明了“降水”这个随机事件发生的概率,我们知道:在一次试验中,概率为90%的事件也可能不出现,因此,“昨天没有下雨”并不说明“昨天的降水概率为90%”的天气预报是错误的。
*
*
4.天气预报的概率解释
天气预报是气象专家根据观测到的气象资料和专家们的实际经验,经过分析推断得到的.它不是本书上定义的概率,而是主观概率的一种.
*
*
5.试验与发现
6.遗传机理中的统计规律
孟德尔(Gregor Mendel,1822-1884)孟德尔是现代遗传学之父,是这一门重要生物学科的奠基人。1865年发现遗传定律。
*
*
孟德尔的豌豆杂交试验
孟德尔把黄色和绿色的豌豆杂交,第一年收获的豌豆是黄色的。第二年,当他把第一年收获的黄色豌豆再种下时,收获的豌豆既有黄色的又有绿色的。
类似地,他把圆形和皱皮豌豆杂交,第一年收获的都是圆形豌豆,连一粒皱皮豌豆都没有。第二年,当他把这种杂交圆形再种下时,得到的却既有圆形豌豆,又有皱皮豌豆。
*
*
*
*
yy
YY
YY
Yy
Yy
Yy
Yy
亲 本
第一代
第二代
yy
豌豆杂交试验
概率
*
*
1.投掷一枚骰子(均匀的正方体),设事件A为“掷得偶数点”,事件B为“掷得奇数点”,则P(A)与P(B)的大小关系为()
A.P(A)>P(B) B.P(A)=P(B)
C.P(A)答案:B
*
*
2.在下列各事件中,可能性最大的是( )
A.任意买一张电影票,座位号是奇数
B.掷一枚骰子点数小于等于2
C.有10000张彩票,其中100张是获奖彩票,从中抽一张就得奖
D.一个袋子中有8个红球,2个白球,从中摸出一个是红球
答案:D
*
*
3.对一批产品的长度(单位:mm)进行抽样检测,下图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在区间[15,20)和区间[25,30)上的为二等品,在区间[10,15)和[30,35)上的为三等品.用频率估计概率,现从该批产品中随机抽取一件,则其为二等品的概率为( )
A.0.09 B.0.20 C.0.25 D.0.45
解析:设二等品的频率为a,
根据频率分布直方图得:a+5×0.02+5×0.06+5×0.03=1
a=0.45
*
*
4.某班有50位同学,其中男女各25名,今有这个班的一个学生在街上碰到一个同班同学,则下列结论正确的是( )
A.碰到异性同学比碰到同性同学的概率大
B.碰到同性同学比碰到异性同学的概率大
C.碰到同性同学和异性同学的概率相等
D.碰到同性同学和异性同学的概率随机变化
解析:由题意知本题是一个等可能事件的概率,
试验发生包含的事件数是50,碰到同性同学的事件有24个,碰到异性同学的事件有25个,
∴碰到异性同学的概率比碰到同性同学的概率大
*
*
5.元旦就要到了,某校将举行庆祝活动,每班派1人主持节目.高一(2)班的小明、小华和小利实力相当,又都争着要去,班主任决定用抽签的方式决定.机灵的小强给小华出主意,要小华先抽,说先抽的机会大.你是怎样认为的?说说看.
[解析] 先抽后抽,机会是均等的
3.1.1 随机事件的概率
*
*
财富梦想调查
你有买彩票的经历吗?
买之前你确定能中奖吗?
你意识到买彩票中大奖的机会有多大吗?
七星彩:国家体育总局发行的全国型彩票,共7位数,每一位数均来自0~9这十个数字,那么中一等奖(500万)的概率是多少?
双色球:中国福利彩票中心发行的全国型彩票,从1~33里选出6个数组成六个红球,从1~16里选出1个数构成一个蓝球,这就是双色球,那么中一等奖(500万)的概率是多少?
概率论的诞生,虽然渊源于靠碰运气取胜的游戏,但在今天,却已成为人类知识最重要的一部分.
—— 拉普拉斯(法国数学家)
*
*
下列事件发生与否,各有什么特点呢?
(1)“地球不停地转动”
(2)“木柴燃烧,产生能量”
(3)“在常温下,石头在一天内风化”
(4)“某人投球,三分!”
(5)“掷一枚硬币,出现正面”
(6)“在标准大气压下且温度低于0℃时,雪融化”
必然发生
必然发生
不可能发生
不可能发生
可能发生也可能不发生
可能发生也可能不发生
*
*
定义:
随机事件:
在一定条件下可能发生也可能不发生的事件叫随机事件。
必然事件:
在一定条件下必然要发生的事件叫必然事件。
不可能事件:
在一定条件下不可能发生的事件叫不可能事件。
确定事件和随机事件统称为事件,一般用大写字母A,B,C…表示。
*
*
这些事件发生与否,各有什么特点呢?
(1)“地球不停地转动”
(2)“木柴燃烧,产生能量”
(3)“在常温下,石头在一天内风化”
(4)“某人投球,三分!”
(5)“掷一枚硬币,出现正面”
(6)“在标准大气压下且温度低于0℃时,雪融化”
必然发生
必然发生
不可能发生
不可能发生
可能发生也可能不发生
可能发生也可能不发生
必然事件
必然事件
不可能事件
随机事件
随机事件
不可能事件
*
*
随机事件是在一定条件下可能发生 也可能不发生的事件。
对于随机事件,知道它发生的可能性大小是非常重要的
我们用概率度量随机事件发生的可能性大小。随机事件发生的可能性大则随机事件发生的
概率大;概率小则随机事件发生的可能性小。
我们如何获得随机事件发生的概率?
要了解随机事件发生的可能性大小,最直接的方法就是试验。
*
*
在相同的条件S下重复n次试验,若某一事件A出现的次数为nA,
则称nA为事件A出现的频数,
那么事件A出现的频率fn(A)等于什么?
频率的取值范围是什么?
*
*
让我们来做一个试验:
投掷一枚硬币,出现正面可能性有多大?
*
*
实验 有人将一枚硬币抛掷 5 次、50 次、500 次, 各做7 遍, 观察正面出现的次数及频率.
试验
序号
22
25
21
25
24
18
27
251
249
256
247
251
262
258
0.4
0.6
0.2
1.0
0.2
0.4
0.8
0.44
0.50
0.42
0.48
0.36
0.54
0.502
0.498
0.512
0.494
0.524
0.516
0.50
0.502
波动最小
随n的增大, 频率 f 呈现出稳定性
1
2
3
4
5
6
7
2
3
1
5
1
2
4
*
*
抛掷次数(n) 2048 4040 12000 24000 30000
正面朝上次数(m) 1061 2048 6019 12012 14984
频率(m/n) 0.518 0.506 0.501 0.5005 0.4996
历史上曾有人作过抛掷硬币的大量重复实验,结果如下表所示
抛掷次数n
频率m/n
0.5
1
2048
4040
12000
24000
30000
72088
德 . 摩根
蒲 丰
皮尔逊
皮尔逊
维 尼
*
*
实验中只出现两种结果,没有其它结果,每一次试验的结果不固定,但只是“正面”、“反面”两种中的一种,且它们出现的频率均接近于0.5,但不相等。
(1)在每次实验中可能出现几种实验结果?还有其它实验结果吗?
根据实验分别回答下列问题:
(2)如果同学们再重复一次上面的试验,汇总结果还会和这次汇总结果一致吗
*
*
在大量重复实验后,随着次数的增加,频率会逐渐稳定在区间[0,1]中的某个常数上。
(3)如果允许你做大量重复试验,你认为结果又如何呢?
根据实验分别回答下列问题:
总结:“掷一枚硬币,正面朝上”在一次试验中是否发生不能确定,但随着试验次数的增加,正面朝上的频率逐渐地接近于0.5.
*
*
概率:
经过大量的重复试验,事件A发生的频率会逐渐稳定在区间[0,1]中的某个常数上.
用频率fn(A)来估计概率P(A)
是一个确定的值
试 验 结 论:
这个常数就是事件A发生的概率.
随着试验次数的增加,频率稳定在0.5附近
*
*
一般地,在大量重复进行同一试验时,事件A发生的频率 总是接近于某个常数,在它附近摆动。这个常数叫做事件A的概率,记作P(A)。
通过实验,我们可以发觉:
事件A的概率:
注:
事件A的概率:
(1)频率m/n总在P(A)附近摆动,当n越大时,摆动幅度越小。
(2)0≤P(A)≤1 不可能事件的概率为0,必然事件为1,随机事件的概率大于0而小于1。
(3)大量重复进行同一试验时,随机事件及其概率呈现出规律性。
*
*
☆频率与概率的区别:
1. 事件A发生的频率fn(A)是(不变,变化)的;
事件A发生的概率P(A)是(不变,变化)的;
概率是一个确定的常数,是客观存在的,与每次试验结果无关,与试验次数无关,甚至与做不做试验无关.
2.随着试验次数的增加频率稳定于概率;
3.概率是频率的稳定值,频率是概率的近似值;
因此在实际中我们求一个事件的概率时,有时通过进行大量的重复试验,用这个事件发生的频率近似地作为它的概率.
*
*
概率是频率的稳定值,而频率是概率的近似值。
概率反映了随机事件发生的可能性的大小。
频率与概率的关系
总之:
*
*
1.下列说法正确的是( )
A.任一事件的概率总在(0.1)内
B.不可能事件的概率不一定为0
C.必然事件的概率一定为1
D.以上均不对
解析:必然事件的概率为1,不可能事件的概率为0,随机事件的概率在0到1之间.
故选C.
3.1.2 概率的意义
人生必须去搏,敢于冒风险,对随机事件作出自己的判断,把“不一定”的事情变成现实,这才是“胜利”。
*
*
1.概率的正确理解
1.有人说,既然抛掷一枚硬币出现正面 的概率为0.5,那么连续两次抛掷一枚质地均匀的硬币,一定是一次正面朝上,一次反面朝上。 你认为这种想法正确吗?
2.有人说,中奖率为1/1000的彩票,买1000张一定中奖,这种理解对吗?
*
*
1.概率的正确理解:
有人说,既然抛掷一枚硬币出现正面的概率为0.5,那么连续两次抛掷一枚质地均匀的硬币,一定是一次正面朝上,一次反面朝上,你认为这种想法正确吗
点评:这种想法是错误的.因为连续两次抛掷一枚质地均匀的硬币仅仅是做两次重复的试验,试验的结果仍然是随机的,当然可以两次均出现正面朝上或两次均出现反面朝上.
*
*
点评:不一定.因为每张彩票是否中奖是随机的,1000张彩票有几张中奖也是随机的.这就是说,每张彩票既可能中奖也可能不中奖,因此1000张彩票中可能没有一张中奖,也可能有一张、两张乃至多张中奖.
虽然中奖张数是随机的,但这种随机性中具有规律性.即随着所买彩票张数的增加,其中中奖彩票所占的比例可能越接近于1/1000.
1.概率的正确理解:
有人说,中奖率为1/1000的彩票,买1000张一定中奖,这种理解对吗?
*
*
例如:把同样大小的9个白色乒乓球和1个黄色乒乓球放在一个不透明的袋子中,每次摸出1球后放回袋中,这样摸10次,
(1)每次摸到白球的可能性大还是黄球的可能性大
(2)摸的10次中是否一定至少有1次摸到黄球
点评:每次摸到白球的概率是0.9,而每次摸到黄球的概率为0.1,因此每次摸到白球的可能性要大.
尽管每次摸到黄球的概率为0.1,但摸10次球,不一定能摸到黄球.
*
*
归纳小结:
随机事件在一次试验中发生与否是随机的,但随机中含有规律性.认识了这种随机性中的规律性,就能使我们比较准确地预测随机事件发生的可能性.
*
*
2、游戏的公平性
观察:你有没有注意到在乒乓球、排球等体育比赛前,裁判是如何确定发球权的?你觉得对比赛双方公平吗?
判断发球权的常用方法:裁判员拿出一个抽签器,它是一个像大硬币似的均匀塑料圆板,一面是红圈,一面是绿圈,然后随意指定一名运动员,要他猜上抛的抽签器落到球台上时,是红圈那面朝上还是绿圈那面朝上.如果他猜对了,就由他先发球,否则,由另一方先发球.
*
*
2.游戏的公平性
分析:因为抽签器上抛后,红圈朝上与绿圈朝上的概率都是0.5,因此任何一名运动员猜中的概率都是0.5,也就是每个运动员取得发球权的概率均为0.5,所以这个规则是公平的.
*
*
这样的游戏公平吗
小军和小民玩掷骰子是游戏,他们约定:两颗骰子掷出去,如果朝上的两个数的和是5,那么小军获胜,如果朝上的两个数的和是7,那么小民获胜.这样的游戏公平吗?
事件:掷双骰子
A:朝上两个数的和是5
B:朝上两个数的和是7
关键是比较A发生的可能性和B发
生的可能性的大小.
*
*
1点 2点 3点 4点 5点 6点
1点 2 3 4 5 6 7
2点 3 4 5 6 7 8
3点 4 5 6 7 8 9
4点 5 6 7 8 9 10
5点 6 7 8 9 10 11
6点 7 8 9 10 11 12
观察表中数据,可发现,做同时掷两枚硬币的试验时,事件A发生的可能性(4种情况)比事件B发生的可能性(6种情况)小,即P(A)
*
3.决策中的概率思想:
〖思考〗连续掷硬币1000次,结果1000次全部是正面朝上,出现这样的结果,你会怎样想
〖思考〗如果一个袋中有99个红球,1个白球,或者有99个白球,1个红球,事先不知道到底是哪种情况.一个人从袋中随机摸出1球,结果发现是红球,你认为这个袋中是有99个红球,1个白球,还是有99个白球,1个红球呢
*
*
如果我们面临的是从多个可选答案中挑选正确答案的决策任务,那么“使得样本出现的可能性最大”可以作为决策的准则,这种判断问题的方法称为极大似然法。
极大似然法是统计中重要的统计思想方法之一。
*
*
1.设某厂产品的次品率为2%,估算该厂8000件产品中合格品的件数可能为()
A.160件 B.7840件 C.7998件 D.7800件
*
*
4.天气预报的概率解释
〖思考〗某地气象局预报说,明天本地降水概率为70%,你认为下面两个解释中哪一个代表气象局的观点
(1)明天本地有70%的区域下雨,30%的区域不下雨;
(2)明天本地下雨的机会是70%.
√
*
*
例:生活中,我们经常听到这样的议论:“天气预报说昨天降水概率为90%,结果根本一点雨都没下,天气预报也太不准确了。”这样的说法对吗,你能给出解释吗?
解:天气预报的“降水”是一个随机事件,概率为90%指明了“降水”这个随机事件发生的概率,我们知道:在一次试验中,概率为90%的事件也可能不出现,因此,“昨天没有下雨”并不说明“昨天的降水概率为90%”的天气预报是错误的。
*
*
4.天气预报的概率解释
天气预报是气象专家根据观测到的气象资料和专家们的实际经验,经过分析推断得到的.它不是本书上定义的概率,而是主观概率的一种.
*
*
5.试验与发现
6.遗传机理中的统计规律
孟德尔(Gregor Mendel,1822-1884)孟德尔是现代遗传学之父,是这一门重要生物学科的奠基人。1865年发现遗传定律。
*
*
孟德尔的豌豆杂交试验
孟德尔把黄色和绿色的豌豆杂交,第一年收获的豌豆是黄色的。第二年,当他把第一年收获的黄色豌豆再种下时,收获的豌豆既有黄色的又有绿色的。
类似地,他把圆形和皱皮豌豆杂交,第一年收获的都是圆形豌豆,连一粒皱皮豌豆都没有。第二年,当他把这种杂交圆形再种下时,得到的却既有圆形豌豆,又有皱皮豌豆。
*
*
*
*
yy
YY
YY
Yy
Yy
Yy
Yy
亲 本
第一代
第二代
yy
豌豆杂交试验
概率
*
*
1.投掷一枚骰子(均匀的正方体),设事件A为“掷得偶数点”,事件B为“掷得奇数点”,则P(A)与P(B)的大小关系为()
A.P(A)>P(B) B.P(A)=P(B)
C.P(A)
*
*
2.在下列各事件中,可能性最大的是( )
A.任意买一张电影票,座位号是奇数
B.掷一枚骰子点数小于等于2
C.有10000张彩票,其中100张是获奖彩票,从中抽一张就得奖
D.一个袋子中有8个红球,2个白球,从中摸出一个是红球
答案:D
*
*
3.对一批产品的长度(单位:mm)进行抽样检测,下图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在区间[15,20)和区间[25,30)上的为二等品,在区间[10,15)和[30,35)上的为三等品.用频率估计概率,现从该批产品中随机抽取一件,则其为二等品的概率为( )
A.0.09 B.0.20 C.0.25 D.0.45
解析:设二等品的频率为a,
根据频率分布直方图得:a+5×0.02+5×0.06+5×0.03=1
a=0.45
*
*
4.某班有50位同学,其中男女各25名,今有这个班的一个学生在街上碰到一个同班同学,则下列结论正确的是( )
A.碰到异性同学比碰到同性同学的概率大
B.碰到同性同学比碰到异性同学的概率大
C.碰到同性同学和异性同学的概率相等
D.碰到同性同学和异性同学的概率随机变化
解析:由题意知本题是一个等可能事件的概率,
试验发生包含的事件数是50,碰到同性同学的事件有24个,碰到异性同学的事件有25个,
∴碰到异性同学的概率比碰到同性同学的概率大
*
*
5.元旦就要到了,某校将举行庆祝活动,每班派1人主持节目.高一(2)班的小明、小华和小利实力相当,又都争着要去,班主任决定用抽签的方式决定.机灵的小强给小华出主意,要小华先抽,说先抽的机会大.你是怎样认为的?说说看.
[解析] 先抽后抽,机会是均等的
