2021-2022学年高一数学人A版(2019)数学-选择性必修第三册-第六章 计数原理-§2.2排列数(共24张PPT)
文档属性
| 名称 | 2021-2022学年高一数学人A版(2019)数学-选择性必修第三册-第六章 计数原理-§2.2排列数(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 14:20:07 | ||
图片预览








文档简介
(共24张PPT)
6.2.2排列数
2
从n个不同元素中,任取m(m≤n)个元素(m个元素不可重复取)按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
1、排列的定义:
2、排列问题的判断方法:
(1) 元素的无重复性 (2) 元素的有序性
判断关键是看选出的元素有没有顺序要求.
3.利用“树形图”法解决简单排列问题的适用范围及策略
(1)适用范围:“树形图”在解决排列元素个数不多的问题时,是一种比较有效的表示方式.
(2)策略:在操作中先将元素按一定顺序排出,然后以先安排哪个元素为分类标准进行分类,再安排第二个元素,并按此元素分类,依次进行,直到完成一个排列,这样能做到不重不漏,然后再按树形图写出排列.
1.掌握排列数公式及其变式,并能运用排列数公式熟练地进行相关计算和证明.2.掌握有限制条件的排列应用题的一些常用方法,并能运用排列的相关知识解一些简单的排列应用题.
1.通过学习排列数公式,体现了数学抽象的素养.
2.借助排列数公式进行计算,培养数学运算的素养.
3.通过排列知识解决实际问题,提升逻辑推理和数学运算的素养.
课标要求
素养要求
思考2:写出从5个元素a,b,c,d,e中任取2个元素的所有排列.
解决办法是先画“树形图”,再由此写出所有的排列,共20个.
若把这题改为:写出从5个元素a,b,c,d,e中任取3个元素的所有排列,结果如何呢?
思考1:在A、B、C、D四位候选人中选举正、副班长各一人共有几种不同的选法?写出所有可能的选举结果.
AB AC AD BA BC BD CA CB CD DA DB DC
探究点1 排列数
研究一个排列问题,往往只需知道所有排列的个数而无需一一写出所有的排列,那么能否不通过一一写出所有的排列而直接“得”出所有排列的个数呢?接下来我们将来共同探讨这个问题:排列数及其公式.
方法仍然照用,但数字将更大,写起来更“啰嗦”.
1.排列数:
从n个不同的元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同的元素中取出m个元素的排列数。用符号表示.
“排列”和“排列数”有什么区别和联系?
“一个排列”是指:从n个不同元素中,任取m个元素按照一定的顺序排成一列,不是数;
“排列数”是指:从n个不同元素中,任取m个元素所有排列的个数,是一个数;所以符号只表示排列数,而不表示具体的排列.
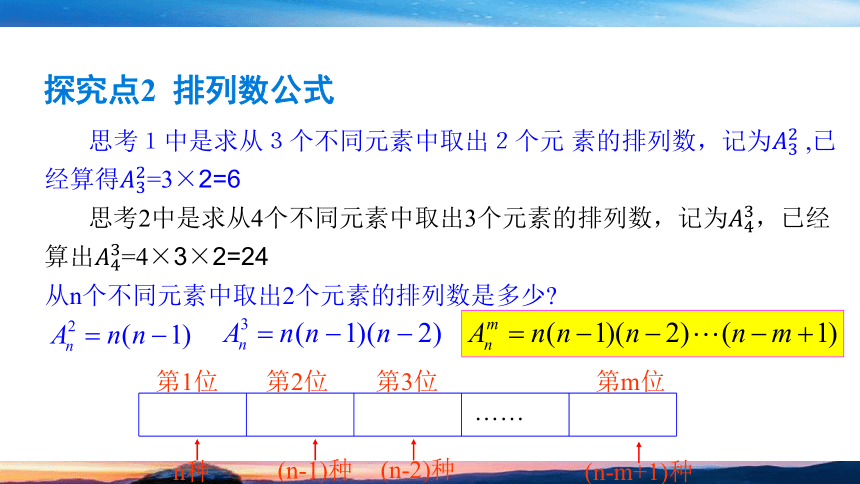
思考1中是求从3个不同元素中取出2个元 素的排列数,记为 ,已经算得=3×2=6
思考2中是求从4个不同元素中取出3个元素的排列数,记为,已经算出=4×3×2=24
从n个不同元素中取出2个元素的排列数是多少
……
第1位
第2位
第3位
第m位
n种
(n-1)种
(n-2)种
(n-m+1)种
探究点2 排列数公式
(1)排列数公式(1):
当m=n时,
正整数1到n的连乘积,叫做n的阶乘,用n!表示.
n个不同元素的全排列公式:
(2)排列数公式(2):
为了使当m=n时上面的公式也成立,规定:0!=1.
m个因式
说明:
①排列数公式的第一个常用来计算,第二个常用来证明.
②.对于m≤n这个条件要留意,往往是解方程时的隐含条件.
例3. 计算:(1)
解 根据排列
(1)
(2)
(3)
(4)
由例3可以
即
例4 用0~9这10个数字,可以组成多少个没有重复数字的三位数?
解法1:由于三位数的百位上的数字不能是0,所以可以分两步完成:
第1步,确定百位上的数字可以从1~9这9个数字中取出1个,有种取法;第2步,确定十位和个位上的数字,可以从剩下的9个数中取2个, 有种取法; 如图
根据分步乘法计数原理,所求的三位数的个数为 9×9×8648.
分析:在0~9这10个数字中,因为0不能在百位上,而其他9个数字可以在任意数位上,因此0是一个特殊的元素。一般地,我们可以从特殊元素的位置入手来考虑问题.
解法2:如图,符合条件的三位数可以分成三类:第1类,每一位数字都不是0的三位数,可以从1~9这9个数字中取出3个,有种取法;第2类,个位上的数字是0的三位数,可以从剩下的9个数中取出2个放在百位和十位,有种取法;第3类,十位上的数字是0的三位数,可以从剩下的9个数字中取出2个放在百位和个位,有种取法.根据分类加法计数原理,所求三位数的个数为=9×8×7+9×8+9×8=648.
解法3:从0~9这10个数字中选取3个的排列数为,其中0在百位上的排列数为,它们的差就是用这10个数组成的没有重复数字的三位数的个数,
即所求三位数的个数为10×9×89×8648.
1.此类题目从不同的视角可以选择不同的方法,我们用各种方法解决这个题的目的是:希望通过对本题的感悟,能掌握更多的解决这类问题的方法.
2.元素分析法最基本,位置分析法对重要元素区别对待,间接法对对立面比较容易求解的题目特别实用.
【方法规律】
解析:此问题相当于从5个不同元素中取出2个元素的排列数,即共有 =20(种)不同的送书方法.
1.从5本不同的书中选两本送给2名同学,每人一本,则不同的送书方法的种数为( )
A.5 B.10 C.20 D.60
C
19
D
20
21
120
22
23
建立自我、追求忘我.
6.2.2排列数
2
从n个不同元素中,任取m(m≤n)个元素(m个元素不可重复取)按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
1、排列的定义:
2、排列问题的判断方法:
(1) 元素的无重复性 (2) 元素的有序性
判断关键是看选出的元素有没有顺序要求.
3.利用“树形图”法解决简单排列问题的适用范围及策略
(1)适用范围:“树形图”在解决排列元素个数不多的问题时,是一种比较有效的表示方式.
(2)策略:在操作中先将元素按一定顺序排出,然后以先安排哪个元素为分类标准进行分类,再安排第二个元素,并按此元素分类,依次进行,直到完成一个排列,这样能做到不重不漏,然后再按树形图写出排列.
1.掌握排列数公式及其变式,并能运用排列数公式熟练地进行相关计算和证明.2.掌握有限制条件的排列应用题的一些常用方法,并能运用排列的相关知识解一些简单的排列应用题.
1.通过学习排列数公式,体现了数学抽象的素养.
2.借助排列数公式进行计算,培养数学运算的素养.
3.通过排列知识解决实际问题,提升逻辑推理和数学运算的素养.
课标要求
素养要求
思考2:写出从5个元素a,b,c,d,e中任取2个元素的所有排列.
解决办法是先画“树形图”,再由此写出所有的排列,共20个.
若把这题改为:写出从5个元素a,b,c,d,e中任取3个元素的所有排列,结果如何呢?
思考1:在A、B、C、D四位候选人中选举正、副班长各一人共有几种不同的选法?写出所有可能的选举结果.
AB AC AD BA BC BD CA CB CD DA DB DC
探究点1 排列数
研究一个排列问题,往往只需知道所有排列的个数而无需一一写出所有的排列,那么能否不通过一一写出所有的排列而直接“得”出所有排列的个数呢?接下来我们将来共同探讨这个问题:排列数及其公式.
方法仍然照用,但数字将更大,写起来更“啰嗦”.
1.排列数:
从n个不同的元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同的元素中取出m个元素的排列数。用符号表示.
“排列”和“排列数”有什么区别和联系?
“一个排列”是指:从n个不同元素中,任取m个元素按照一定的顺序排成一列,不是数;
“排列数”是指:从n个不同元素中,任取m个元素所有排列的个数,是一个数;所以符号只表示排列数,而不表示具体的排列.
思考1中是求从3个不同元素中取出2个元 素的排列数,记为 ,已经算得=3×2=6
思考2中是求从4个不同元素中取出3个元素的排列数,记为,已经算出=4×3×2=24
从n个不同元素中取出2个元素的排列数是多少
……
第1位
第2位
第3位
第m位
n种
(n-1)种
(n-2)种
(n-m+1)种
探究点2 排列数公式
(1)排列数公式(1):
当m=n时,
正整数1到n的连乘积,叫做n的阶乘,用n!表示.
n个不同元素的全排列公式:
(2)排列数公式(2):
为了使当m=n时上面的公式也成立,规定:0!=1.
m个因式
说明:
①排列数公式的第一个常用来计算,第二个常用来证明.
②.对于m≤n这个条件要留意,往往是解方程时的隐含条件.
例3. 计算:(1)
解 根据排列
(1)
(2)
(3)
(4)
由例3可以
即
例4 用0~9这10个数字,可以组成多少个没有重复数字的三位数?
解法1:由于三位数的百位上的数字不能是0,所以可以分两步完成:
第1步,确定百位上的数字可以从1~9这9个数字中取出1个,有种取法;第2步,确定十位和个位上的数字,可以从剩下的9个数中取2个, 有种取法; 如图
根据分步乘法计数原理,所求的三位数的个数为 9×9×8648.
分析:在0~9这10个数字中,因为0不能在百位上,而其他9个数字可以在任意数位上,因此0是一个特殊的元素。一般地,我们可以从特殊元素的位置入手来考虑问题.
解法2:如图,符合条件的三位数可以分成三类:第1类,每一位数字都不是0的三位数,可以从1~9这9个数字中取出3个,有种取法;第2类,个位上的数字是0的三位数,可以从剩下的9个数中取出2个放在百位和十位,有种取法;第3类,十位上的数字是0的三位数,可以从剩下的9个数字中取出2个放在百位和个位,有种取法.根据分类加法计数原理,所求三位数的个数为=9×8×7+9×8+9×8=648.
解法3:从0~9这10个数字中选取3个的排列数为,其中0在百位上的排列数为,它们的差就是用这10个数组成的没有重复数字的三位数的个数,
即所求三位数的个数为10×9×89×8648.
1.此类题目从不同的视角可以选择不同的方法,我们用各种方法解决这个题的目的是:希望通过对本题的感悟,能掌握更多的解决这类问题的方法.
2.元素分析法最基本,位置分析法对重要元素区别对待,间接法对对立面比较容易求解的题目特别实用.
【方法规律】
解析:此问题相当于从5个不同元素中取出2个元素的排列数,即共有 =20(种)不同的送书方法.
1.从5本不同的书中选两本送给2名同学,每人一本,则不同的送书方法的种数为( )
A.5 B.10 C.20 D.60
C
19
D
20
21
120
22
23
建立自我、追求忘我.
