2021-2022学年高一数学人A版(2019)数学-选择性必修第三册-第六章 计数原理-§2.4组合数(共23张PPT)
文档属性
| 名称 | 2021-2022学年高一数学人A版(2019)数学-选择性必修第三册-第六章 计数原理-§2.4组合数(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 14:21:46 | ||
图片预览








文档简介
(共23张PPT)
6.2.4组合数
某国际会议中心有A,B,C,D和E,共5种不同功能的会议室,且每种功能的会议室又有大、中、小和特小,共4种型号,总共20个会议室.
现在有一个国际学术会议需要选择3种不同功能
的6个会议室,并且每种功能的会议室选2个型号.
试问:会议中心的工作人员安排会议的方法有多少种?
通过本节课的学习我们就能顺利地解决上述问题了!
1.理解组合与组合数的概念.2.会推导组合数公式,并会应用公式求值.3.理解组合数的两个性质,并会求值、化简和证明.
1.通过学习组合与组合数的概念,体现了数学抽象的素养.
2.借助组合数公式及组合数的性质进行运算,培养数学运算的素养..
课标要求
素养要求
1.组合数的定义:
从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号 表示.
例如,从3个不同元素中取出2个元素的组合数,表示为,
从4个不同元素中取出3个元素的组合数,表示为.
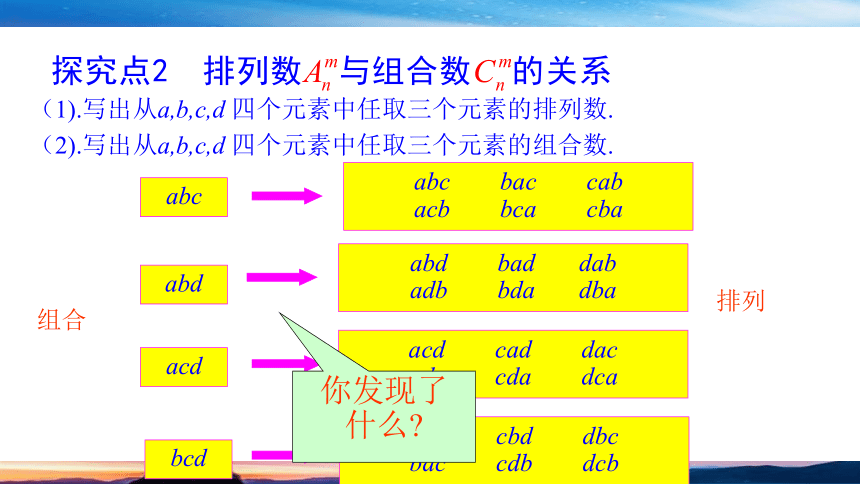
探究点1 组合数与组合数公式
注意:是一个数,应该把它与“组合”区别开来.
思路:从4个不同元素中取出3个元素的组合数,设这4个元素为a,b,c,d,那么从中取出3个元素的排列数 =24,以“元素相同”为标准将这24个排列分组,一共有4组,因此组合数 =4.
思考:前面已经提到,组合和排列有关系,我们能否利用这种关系,由排列数来求组合数呢?
组合
排列
abc
abd
acd
bcd
abc bac cab
acb bca cba
abd bad dab
adb bda dba
acd cad dac
adc cda dca
bcd cbd dbc
bdc cdb dcb
你发现了
什么
(1).写出从a,b,c,d 四个元素中任取三个元素的排列数.
(2).写出从a,b,c,d 四个元素中任取三个元素的组合数.
根据分步计数原理,得到:
因此:
一般地,求从 n个不同元素中取出 m 个元素的排列数,可以分为以下2步:
第1步,先求出从这n个不同元素中取出m个元素的组合数.
第2步,求每一个组合中m个元素的全排列数 .
这里 , 且 ,这个公式叫做组合数公式.
组合数公式:
从 n 个不同元中取出m个元素的排列数
排列数公式:
例6.计算:
(1);(3)
解 根据组合数公式,可得
⑴ 120;
(3)
(4)
公式的不同形式
思考: 分别观察例中(1)与(2),(3)与(4)的结果,你有什么发现和猜想?
【方法规律】
公式的使用技巧
例4 一个口袋内装有大小相同的7个白球和1个黑球.
⑴ 从口袋内取出3个球,共有多少种取法?
⑵ 从口袋内取出3个球,使其中含有1个黑球,有多少种取法?
⑶ 从口袋内取出3个球,使其中不含黑球,有多少种取法?
⑵
⑶
解 ⑴
我们可以这样解释:从口袋内的8个球中所取出的3个球,可以分为两类:一类含有1个黑球,一类不含有黑球.因此根据分类计数原理,上述等式成立.
我们发现:=+为什么呢
注:1 公式特征:下标相同而上标差1的两个组合数之和,等于下标比原下标多1而上标与原组合数上标较大的相同的一个组合数.
2 此性质的作用:恒等变形,简化运算.在今后学习“二项式定理”时,我们会看到它的主要应用.
性质
例7 在100件产品中,有98件合格品,2件次品.从这100件产品中任意抽出3件.
(1)有多少种不同的抽法?
(2)抽出的3件中恰好有1件是次品的抽法有多少种?
(3)抽出的3件中至少有1件是次品的抽法有多少种?
分析:(1)所求的不同抽法的种数,就是从100件产品中取出3件的组合数;
(2)分两步,第一步从2件次品中抽出1件次品,第二步从98件合格品中抽出2件合格品,由乘法原理可得;
(3)可从反面考虑,其反面是抽出的3件全是合格品,求出方法数后,由第(1)题的结论减去这个结果即可得.
组合问题的基本解法
(1)判断是否为组合问题;
(2)是否分类或分步;
(3)根据组合的相关知识进行求解.
归纳总结
18
A
19
D
20
2021
21
课堂小结
只要功夫深,铁杵磨成针.
6.2.4组合数
某国际会议中心有A,B,C,D和E,共5种不同功能的会议室,且每种功能的会议室又有大、中、小和特小,共4种型号,总共20个会议室.
现在有一个国际学术会议需要选择3种不同功能
的6个会议室,并且每种功能的会议室选2个型号.
试问:会议中心的工作人员安排会议的方法有多少种?
通过本节课的学习我们就能顺利地解决上述问题了!
1.理解组合与组合数的概念.2.会推导组合数公式,并会应用公式求值.3.理解组合数的两个性质,并会求值、化简和证明.
1.通过学习组合与组合数的概念,体现了数学抽象的素养.
2.借助组合数公式及组合数的性质进行运算,培养数学运算的素养..
课标要求
素养要求
1.组合数的定义:
从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号 表示.
例如,从3个不同元素中取出2个元素的组合数,表示为,
从4个不同元素中取出3个元素的组合数,表示为.
探究点1 组合数与组合数公式
注意:是一个数,应该把它与“组合”区别开来.
思路:从4个不同元素中取出3个元素的组合数,设这4个元素为a,b,c,d,那么从中取出3个元素的排列数 =24,以“元素相同”为标准将这24个排列分组,一共有4组,因此组合数 =4.
思考:前面已经提到,组合和排列有关系,我们能否利用这种关系,由排列数来求组合数呢?
组合
排列
abc
abd
acd
bcd
abc bac cab
acb bca cba
abd bad dab
adb bda dba
acd cad dac
adc cda dca
bcd cbd dbc
bdc cdb dcb
你发现了
什么
(1).写出从a,b,c,d 四个元素中任取三个元素的排列数.
(2).写出从a,b,c,d 四个元素中任取三个元素的组合数.
根据分步计数原理,得到:
因此:
一般地,求从 n个不同元素中取出 m 个元素的排列数,可以分为以下2步:
第1步,先求出从这n个不同元素中取出m个元素的组合数.
第2步,求每一个组合中m个元素的全排列数 .
这里 , 且 ,这个公式叫做组合数公式.
组合数公式:
从 n 个不同元中取出m个元素的排列数
排列数公式:
例6.计算:
(1);(3)
解 根据组合数公式,可得
⑴ 120;
(3)
(4)
公式的不同形式
思考: 分别观察例中(1)与(2),(3)与(4)的结果,你有什么发现和猜想?
【方法规律】
公式的使用技巧
例4 一个口袋内装有大小相同的7个白球和1个黑球.
⑴ 从口袋内取出3个球,共有多少种取法?
⑵ 从口袋内取出3个球,使其中含有1个黑球,有多少种取法?
⑶ 从口袋内取出3个球,使其中不含黑球,有多少种取法?
⑵
⑶
解 ⑴
我们可以这样解释:从口袋内的8个球中所取出的3个球,可以分为两类:一类含有1个黑球,一类不含有黑球.因此根据分类计数原理,上述等式成立.
我们发现:=+为什么呢
注:1 公式特征:下标相同而上标差1的两个组合数之和,等于下标比原下标多1而上标与原组合数上标较大的相同的一个组合数.
2 此性质的作用:恒等变形,简化运算.在今后学习“二项式定理”时,我们会看到它的主要应用.
性质
例7 在100件产品中,有98件合格品,2件次品.从这100件产品中任意抽出3件.
(1)有多少种不同的抽法?
(2)抽出的3件中恰好有1件是次品的抽法有多少种?
(3)抽出的3件中至少有1件是次品的抽法有多少种?
分析:(1)所求的不同抽法的种数,就是从100件产品中取出3件的组合数;
(2)分两步,第一步从2件次品中抽出1件次品,第二步从98件合格品中抽出2件合格品,由乘法原理可得;
(3)可从反面考虑,其反面是抽出的3件全是合格品,求出方法数后,由第(1)题的结论减去这个结果即可得.
组合问题的基本解法
(1)判断是否为组合问题;
(2)是否分类或分步;
(3)根据组合的相关知识进行求解.
归纳总结
18
A
19
D
20
2021
21
课堂小结
只要功夫深,铁杵磨成针.
