2021-2022学年高一数学人A版(2019)数学-选择性必修第三册-第七章 随机变量及其分布-§1.1条件概率(共28张PPT)
文档属性
| 名称 | 2021-2022学年高一数学人A版(2019)数学-选择性必修第三册-第七章 随机变量及其分布-§1.1条件概率(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
7.1.1条件概率
彩票摇号试验、抛掷一枚均匀硬币的试验及掷一枚质地均匀骰子的试验,它们具有如下共同特征;
(1)有限性:样本空间的样本点只有有限个;
(2)等可能性:每个样本点发生的可能性相等.
我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型(classical models of probability),简称古典概型.
一般地,设试验E是古典概型,样本空间Ω包含n个样本点,事件A包含其中的k个样本点,则定义事件A的概率
其中,n(A)和n(Ω)分别表示事件A和样本空间Ω包含的样本点个数.
1.了解条件概率的概念.2.掌握求条件概率的两种方法.3.能利用条件概率公式解决一些简单的实际问题.
1.通过条件概率的学习,体会数学抽象的素养.
2.借助条件概率公式解题,提升数学运算素养.
课标要求
素养要求
在必修“概率”一章的学习中,我们遇到过求同一试验中两个事件A与B同时发生(积事件AB)的概率的问题.当事件A与B相互独立时,有
P(AB)=P(A)P(B).
如果事件A与B不独立,如何表示积事件AB的概率呢?
探究点1 条件概率
问题1:某个家庭有2个孩子,问:
(1)两个孩子都是女孩的概率?
(2)如果有1个孩子是女孩,那么两个孩子都是女孩的概率又是多少?
(1)设A=“有1个孩子是女孩”,B=“2个孩子都是女孩”.
条件
所以
(2)“如果有1个孩子是女孩,两个孩子都是女孩”的概率就是“在事件 发生的条件下,事件 发生”的概率,记为
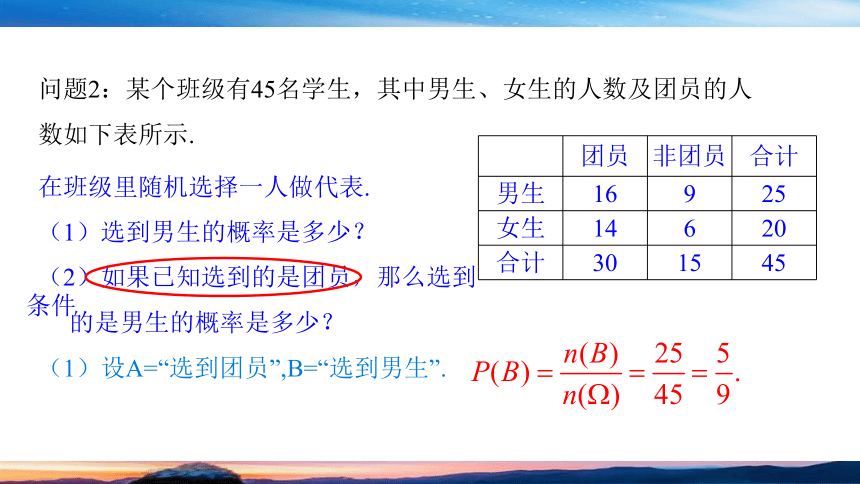
问题2:某个班级有45名学生,其中男生、女生的人数及团员的人数如下表所示.
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
在班级里随机选择一人做代表.
(1)选到男生的概率是多少?
(2)如果已知选到的是团员,那么选到
的是男生的概率是多少?
(1)设A=“选到团员”,B=“选到男生”.
条件
问题2:某个班级有45名学生,其中男生、女生的人数及团员的人数如下表所示.
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
在班级里随机选择一人做代表.
(2)如果已知选到的是团员,那么选到
的是男生的概率是多少?
条件
(2)“在选到团员的条件下,选到男生”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为
所以
分析:求 的一般思想
AB
A
B
W
因为已经知道事件A必然发生,所以只需在A发生的范围内考虑问题,即现在的样本空间为A.
因为在事件A发生的情况下事件B发生,等价于事件A和事件B同时发生,即AB发生.
所以事件A发生的条件下,事件B发生的概率.
为了把这个式子推广到一般情形,不妨记原来的
样本空间为W,则有
AB
A
B
W
条件概率的定义:
在原样本空间的概率
一般地,设A,B为两个随机事件,且P(A)>0,我们称
为在事件A发生的条件下,事件B发生的条件概率.简称条件概率.
一般把P(B|A)读作A发生的条件下B发生的概率.
由条件概率 可得:
对于任意两个事件A与B,若P(A)>0,
概率乘法公式
例1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的 题不再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
分析 如果把“第1次抽到代数题”和“第2次抽到几何题”作为两个事件,那么问题(1)就是积事件的概率,问题(2)就是条件概率.可以先求积事件的概率,再用条件概率公式求条件概率;也可以先求条件概率,再用乘法公式求积事件的概率.
解法1:设A=“第1次抽到代数题”,B=“第2次抽到几何题”。
(1)“第1次抽到代数题且第2次抽到几何题”就是事件AB.从5道试题中每次不放回地随机抽取2道,试验的样本空间Ω包含20个等可能的样本点,即.
因为n(AB)= ,
(2)“在第1次抽到代数题的条件下,第2次抽到几何题”的概率就是事件A发生的条件下,事件B发生的概率。显然P(A)=.利用条件概率公式,得
解法2:在缩小的样本空间A上求P(B|A).已知第1次抽到代数题,
这时还余下4道试题,其中代数题和几何题各2道.
因此,事件A发生的条件下,事件B发生的概率为
P(B|A)=
又P(A)= ,利用乘法公式可得
P(AB)=P(A) P(B|A)= =
求条件概率有两种方法:
方法一:基于样本空间Ω,先计算P(A)和P(AB),再利用条件概率公式求P(B|A)=;
方法二:根据条件概率的直观意义,增加了“A发生”的条件后,样本空间缩小为A,求P(B|A)就是以A为样本空间计算AB的概率.
【方法规律】
条件概率的性质
条件概率只是缩小了样本空间,因此条件概率同样具有概率的性质.
设P(A)>0,则
(1)P(Ω|A)=1;
(2)如果B和C是两个互斥事件,则P(BUC |A)=P(B | A)+P(C | A);
(3)设B和互为对立事件,则P( |A)=1 P(B|A).
探究点2 条件概率的性质
例2 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张.他们中奖的概率与抽奖的次序有关吗?
用A,B,C分别表示甲、乙、丙中奖的事件,则B=.
因为P(A)= P(B)= P(C),所以中奖的概率与抽奖的次序无关.
例3 银行储蓄卡的密码由6位数字组成.某人在银行自助取款机上取钱时,忘记了码的最后1位数字.求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率.
解 (1)设Ai=“第i次按对密码”(i=1,2),则事件“不超过2次就按对密码”可表示为A=A1UA2.
事件A1与事件A2互斥,由概率的加法公式及乘法公式,得
P(A)=P(A1)+P( A2 )= P(A1) +P ) P( A2 | ) =
因此,任意按最后1位数字,不超过2次就按对的概率为.
(2)设B=“最后1位密码为偶数”,则
P(A|B)=P(A1|B)+P(A2|B)== ;
因此,如果记得密码的最后1位是偶数,不超过2次就按对的概率为.
C
B
0.5
0.75
不为模糊不清的未来担忧,只为清清楚楚的现在努力.
7.1.1条件概率
彩票摇号试验、抛掷一枚均匀硬币的试验及掷一枚质地均匀骰子的试验,它们具有如下共同特征;
(1)有限性:样本空间的样本点只有有限个;
(2)等可能性:每个样本点发生的可能性相等.
我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型(classical models of probability),简称古典概型.
一般地,设试验E是古典概型,样本空间Ω包含n个样本点,事件A包含其中的k个样本点,则定义事件A的概率
其中,n(A)和n(Ω)分别表示事件A和样本空间Ω包含的样本点个数.
1.了解条件概率的概念.2.掌握求条件概率的两种方法.3.能利用条件概率公式解决一些简单的实际问题.
1.通过条件概率的学习,体会数学抽象的素养.
2.借助条件概率公式解题,提升数学运算素养.
课标要求
素养要求
在必修“概率”一章的学习中,我们遇到过求同一试验中两个事件A与B同时发生(积事件AB)的概率的问题.当事件A与B相互独立时,有
P(AB)=P(A)P(B).
如果事件A与B不独立,如何表示积事件AB的概率呢?
探究点1 条件概率
问题1:某个家庭有2个孩子,问:
(1)两个孩子都是女孩的概率?
(2)如果有1个孩子是女孩,那么两个孩子都是女孩的概率又是多少?
(1)设A=“有1个孩子是女孩”,B=“2个孩子都是女孩”.
条件
所以
(2)“如果有1个孩子是女孩,两个孩子都是女孩”的概率就是“在事件 发生的条件下,事件 发生”的概率,记为
问题2:某个班级有45名学生,其中男生、女生的人数及团员的人数如下表所示.
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
在班级里随机选择一人做代表.
(1)选到男生的概率是多少?
(2)如果已知选到的是团员,那么选到
的是男生的概率是多少?
(1)设A=“选到团员”,B=“选到男生”.
条件
问题2:某个班级有45名学生,其中男生、女生的人数及团员的人数如下表所示.
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
在班级里随机选择一人做代表.
(2)如果已知选到的是团员,那么选到
的是男生的概率是多少?
条件
(2)“在选到团员的条件下,选到男生”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为
所以
分析:求 的一般思想
AB
A
B
W
因为已经知道事件A必然发生,所以只需在A发生的范围内考虑问题,即现在的样本空间为A.
因为在事件A发生的情况下事件B发生,等价于事件A和事件B同时发生,即AB发生.
所以事件A发生的条件下,事件B发生的概率.
为了把这个式子推广到一般情形,不妨记原来的
样本空间为W,则有
AB
A
B
W
条件概率的定义:
在原样本空间的概率
一般地,设A,B为两个随机事件,且P(A)>0,我们称
为在事件A发生的条件下,事件B发生的条件概率.简称条件概率.
一般把P(B|A)读作A发生的条件下B发生的概率.
由条件概率 可得:
对于任意两个事件A与B,若P(A)>0,
概率乘法公式
例1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的 题不再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
分析 如果把“第1次抽到代数题”和“第2次抽到几何题”作为两个事件,那么问题(1)就是积事件的概率,问题(2)就是条件概率.可以先求积事件的概率,再用条件概率公式求条件概率;也可以先求条件概率,再用乘法公式求积事件的概率.
解法1:设A=“第1次抽到代数题”,B=“第2次抽到几何题”。
(1)“第1次抽到代数题且第2次抽到几何题”就是事件AB.从5道试题中每次不放回地随机抽取2道,试验的样本空间Ω包含20个等可能的样本点,即.
因为n(AB)= ,
(2)“在第1次抽到代数题的条件下,第2次抽到几何题”的概率就是事件A发生的条件下,事件B发生的概率。显然P(A)=.利用条件概率公式,得
解法2:在缩小的样本空间A上求P(B|A).已知第1次抽到代数题,
这时还余下4道试题,其中代数题和几何题各2道.
因此,事件A发生的条件下,事件B发生的概率为
P(B|A)=
又P(A)= ,利用乘法公式可得
P(AB)=P(A) P(B|A)= =
求条件概率有两种方法:
方法一:基于样本空间Ω,先计算P(A)和P(AB),再利用条件概率公式求P(B|A)=;
方法二:根据条件概率的直观意义,增加了“A发生”的条件后,样本空间缩小为A,求P(B|A)就是以A为样本空间计算AB的概率.
【方法规律】
条件概率的性质
条件概率只是缩小了样本空间,因此条件概率同样具有概率的性质.
设P(A)>0,则
(1)P(Ω|A)=1;
(2)如果B和C是两个互斥事件,则P(BUC |A)=P(B | A)+P(C | A);
(3)设B和互为对立事件,则P( |A)=1 P(B|A).
探究点2 条件概率的性质
例2 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张.他们中奖的概率与抽奖的次序有关吗?
用A,B,C分别表示甲、乙、丙中奖的事件,则B=.
因为P(A)= P(B)= P(C),所以中奖的概率与抽奖的次序无关.
例3 银行储蓄卡的密码由6位数字组成.某人在银行自助取款机上取钱时,忘记了码的最后1位数字.求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率.
解 (1)设Ai=“第i次按对密码”(i=1,2),则事件“不超过2次就按对密码”可表示为A=A1UA2.
事件A1与事件A2互斥,由概率的加法公式及乘法公式,得
P(A)=P(A1)+P( A2 )= P(A1) +P ) P( A2 | ) =
因此,任意按最后1位数字,不超过2次就按对的概率为.
(2)设B=“最后1位密码为偶数”,则
P(A|B)=P(A1|B)+P(A2|B)== ;
因此,如果记得密码的最后1位是偶数,不超过2次就按对的概率为.
C
B
0.5
0.75
不为模糊不清的未来担忧,只为清清楚楚的现在努力.
