人教版初中数学九年级上册24.2.2直线与圆的位置关系 课件 (共20张PPT)
文档属性
| 名称 | 人教版初中数学九年级上册24.2.2直线与圆的位置关系 课件 (共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 303.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-19 10:14:11 | ||
图片预览







文档简介
(共20张PPT)
24.2.2直线和圆的位置关系
复习提问:
?
1、什么叫
点到直线的距离?
2、连结直线外一点与直线上所有点
的线段中,最短的是______
直线外一点到这条直线的
垂线段的长度叫点到直线 的距离。
垂线段
.E
.
D
a
欣赏
海上日出
观 察
(1)如图,思考在太阳升起的过程中,太阳和地平线会有几种位置关系?我们把太阳看作一个圆,地平线看作一条直线,由此你能得出直线和圆的位置关系吗?
观 察
(1)如图,思考在太阳升起的过程中,太阳和地平线会有几种位置关系?我们把太阳看作一个圆,地平线看作一条直线,由此你能得出直线和圆的位置关系吗?
观 察
(1)如图,思考在太阳升起的过程中,太阳和地平线会有几种位置关系?我们把太阳看作一个圆,地平线看作一条直线,由此你能得出直线和圆的位置关系吗?
(2)如图,在纸上画一条直线 l,把钥匙环看作一个圆,在纸上移动钥匙环,你能发现在钥匙环移动的过程中,它与直线l的公共点的个数吗?
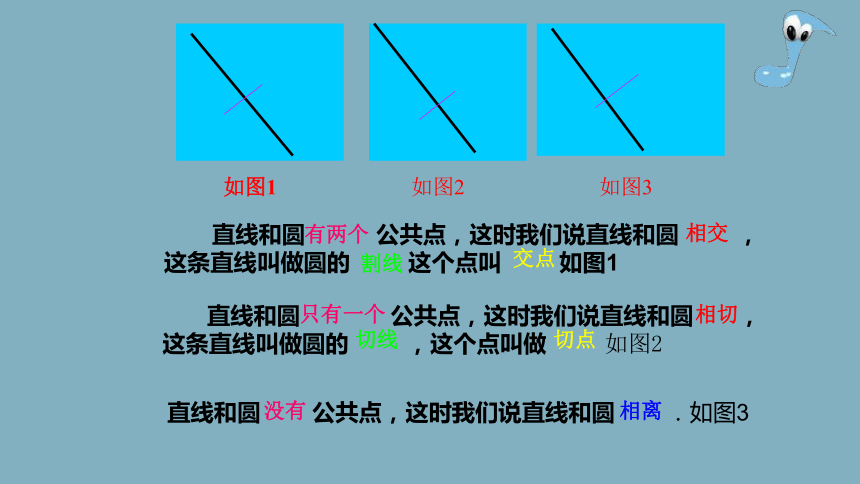
直线和圆 公共点,这时我们说直线和圆 ,这条直线叫做圆的 这个点叫 如图1
直线和圆 公共点,这时我们说直线和圆 .如图3
直线和圆 公共点,这时我们说直线和圆 ,这条直线叫做圆的 ,这个点叫做 如图2
如图1
如图2
如图3
有两个
相交
割线
只有一个
相切
切线
切点
没有
相离
交点
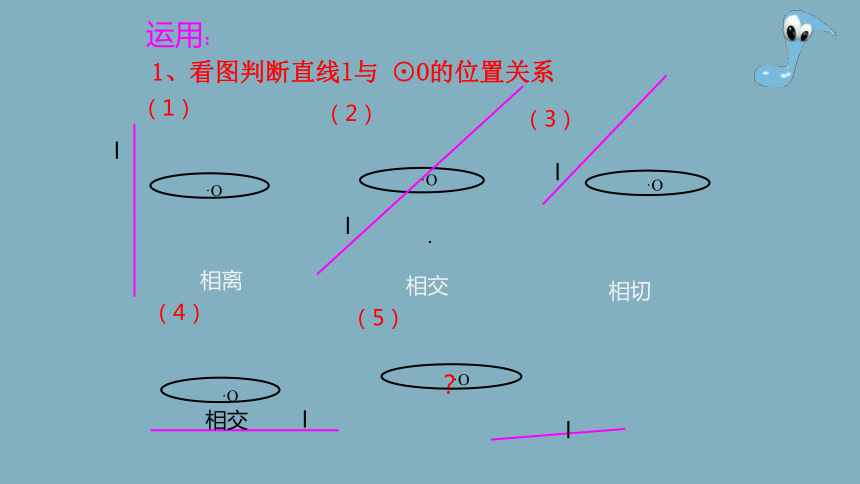
运用:
1、看图判断直线l与 ⊙O的位置关系
(1)
(2)
(3)
(4)
(5)
相离
相切
相交
相交
?
l
l
l
l
l
·O
·O
·O
·O
·O
(5)
?
l
如果,公共点的个数不好判断,该怎么办?
·O
“直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析?
·
A
·
B
d
d
d
.O
.O
.O
r
r
r
相离
相切
相交
1、直线与圆相离 => d>r
2、直线与圆相切 => d=r
3、直线与圆相交 => da
a
a
.A
.B
.
C
.D
.E
.F
. N
H.
Q.
设⊙o的半径为r,直线a到圆心o的距离为d,在直线和圆的不同位置关系中,d与r具有怎样的大小关系?反过来,你能根据d与r的大小关系来确定直线和圆的位置关系吗?
思考
?
<
<
<
判定直线与圆的位置关系的方法有____种:
(1)由 _____________________的个数来判断;
(2)由_________________________ 的关系
来判断。
两
直线与圆的公共点
半径r与圆心到直线的距离d
小结:
1、直线与圆最多有两个公共
点 。…………………( )
2、若直线与圆相交,则直线上的
点都在圆内。… … … …( )
3 、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )
√
×
?
一、判断
.A
.B
.C
.O
.O
m
×
.A
.B
.O
二、填空:
1、已知⊙O的半径为4cm,O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点为____个。
2、已知⊙O的半径是5cm,O到直线a的距离是5cm,则⊙O与直线a的位置关系是 ____。
动动脑筋
相交
相切
两
根据直线和圆相切的定义,经过点A用直尺近似地画出⊙O的切线.
·
A
O
试一试
在码头A与半径为6海里的圆形岛屿M之间有一个海岛,离该岛中心P的12海里范围内是一个暗礁区;现要在码头A与岛屿M之间开辟一条直线型的航线,如果你是航
线设计师,在不考虑距离成本的因素下,你会怎么设计航线?
生活中的应用
H
1、如图,OA垂直直线l于点A,OA= 2 。以r为半径的⊙O与直线l有怎样的位置关系?
(1)r =2
∵ OA< r ∴直线l与⊙O相交
∵OA = r ∴直线l与⊙O相切
(2)r =1
(3)r = 3
∵OA> r ∴直线l与⊙O相离
小试牛刀
3、当r满足_________ 时,
⊙C与直线AB相离.
Rt△ABC,∠C=90°AC=3,BC=4,以C为圆心,设圆的半径为r
r<2.4
r=2.4
r>2.4
0<
A
B
C
D
4
3
2.4
r≥2.4
变式
1、当r满足_________时,
⊙C与直线AB相切.
2、当r满足_________ 时,
⊙C与直线AB相交.
4、当r满足_______时,⊙C与直线AB有公共点.
已知:如图,P为∠ABC的角平分线上一点,⊙P与BC相切.求证:⊙P与AB相切.
练一练:
直线与圆的位置关系
直线与圆的位置关系 相交 相切 相离
公 共 点 个 数
公 共 点 名 称
直 线 名 称
图 形
圆心到直线距离d与半径r的关系
d归纳与小结
d=r
d>r
2
交点
割线
1
切点
切线
0
24.2.2直线和圆的位置关系
复习提问:
?
1、什么叫
点到直线的距离?
2、连结直线外一点与直线上所有点
的线段中,最短的是______
直线外一点到这条直线的
垂线段的长度叫点到直线 的距离。
垂线段
.E
.
D
a
欣赏
海上日出
观 察
(1)如图,思考在太阳升起的过程中,太阳和地平线会有几种位置关系?我们把太阳看作一个圆,地平线看作一条直线,由此你能得出直线和圆的位置关系吗?
观 察
(1)如图,思考在太阳升起的过程中,太阳和地平线会有几种位置关系?我们把太阳看作一个圆,地平线看作一条直线,由此你能得出直线和圆的位置关系吗?
观 察
(1)如图,思考在太阳升起的过程中,太阳和地平线会有几种位置关系?我们把太阳看作一个圆,地平线看作一条直线,由此你能得出直线和圆的位置关系吗?
(2)如图,在纸上画一条直线 l,把钥匙环看作一个圆,在纸上移动钥匙环,你能发现在钥匙环移动的过程中,它与直线l的公共点的个数吗?
直线和圆 公共点,这时我们说直线和圆 ,这条直线叫做圆的 这个点叫 如图1
直线和圆 公共点,这时我们说直线和圆 .如图3
直线和圆 公共点,这时我们说直线和圆 ,这条直线叫做圆的 ,这个点叫做 如图2
如图1
如图2
如图3
有两个
相交
割线
只有一个
相切
切线
切点
没有
相离
交点
运用:
1、看图判断直线l与 ⊙O的位置关系
(1)
(2)
(3)
(4)
(5)
相离
相切
相交
相交
?
l
l
l
l
l
·O
·O
·O
·O
·O
(5)
?
l
如果,公共点的个数不好判断,该怎么办?
·O
“直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析?
·
A
·
B
d
d
d
.O
.O
.O
r
r
r
相离
相切
相交
1、直线与圆相离 => d>r
2、直线与圆相切 => d=r
3、直线与圆相交 => d
a
a
.A
.B
.
C
.D
.E
.F
. N
H.
Q.
设⊙o的半径为r,直线a到圆心o的距离为d,在直线和圆的不同位置关系中,d与r具有怎样的大小关系?反过来,你能根据d与r的大小关系来确定直线和圆的位置关系吗?
思考
?
<
<
<
判定直线与圆的位置关系的方法有____种:
(1)由 _____________________的个数来判断;
(2)由_________________________ 的关系
来判断。
两
直线与圆的公共点
半径r与圆心到直线的距离d
小结:
1、直线与圆最多有两个公共
点 。…………………( )
2、若直线与圆相交,则直线上的
点都在圆内。… … … …( )
3 、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )
√
×
?
一、判断
.A
.B
.C
.O
.O
m
×
.A
.B
.O
二、填空:
1、已知⊙O的半径为4cm,O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点为____个。
2、已知⊙O的半径是5cm,O到直线a的距离是5cm,则⊙O与直线a的位置关系是 ____。
动动脑筋
相交
相切
两
根据直线和圆相切的定义,经过点A用直尺近似地画出⊙O的切线.
·
A
O
试一试
在码头A与半径为6海里的圆形岛屿M之间有一个海岛,离该岛中心P的12海里范围内是一个暗礁区;现要在码头A与岛屿M之间开辟一条直线型的航线,如果你是航
线设计师,在不考虑距离成本的因素下,你会怎么设计航线?
生活中的应用
H
1、如图,OA垂直直线l于点A,OA= 2 。以r为半径的⊙O与直线l有怎样的位置关系?
(1)r =2
∵ OA< r ∴直线l与⊙O相交
∵OA = r ∴直线l与⊙O相切
(2)r =1
(3)r = 3
∵OA> r ∴直线l与⊙O相离
小试牛刀
3、当r满足_________ 时,
⊙C与直线AB相离.
Rt△ABC,∠C=90°AC=3,BC=4,以C为圆心,设圆的半径为r
r<2.4
r=2.4
r>2.4
0<
A
B
C
D
4
3
2.4
r≥2.4
变式
1、当r满足_________时,
⊙C与直线AB相切.
2、当r满足_________ 时,
⊙C与直线AB相交.
4、当r满足_______时,⊙C与直线AB有公共点.
已知:如图,P为∠ABC的角平分线上一点,⊙P与BC相切.求证:⊙P与AB相切.
练一练:
直线与圆的位置关系
直线与圆的位置关系 相交 相切 相离
公 共 点 个 数
公 共 点 名 称
直 线 名 称
图 形
圆心到直线距离d与半径r的关系
d
d=r
d>r
2
交点
割线
1
切点
切线
0
同课章节目录
