2021-2022学年高一上学期数学苏教版(2019)必修第一册-第6章 幂函数、指数函数和对数函数 期末综合复习卷(Word含答案解析)
文档属性
| 名称 | 2021-2022学年高一上学期数学苏教版(2019)必修第一册-第6章 幂函数、指数函数和对数函数 期末综合复习卷(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 564.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 14:34:11 | ||
图片预览




文档简介
第6章 幂函数、指数函数和对数函数 期末综合复习卷
一、单选题
1.若,,则下列关系式中正确的是( )
A. B.
C. D.
2.若函数f(x)=|x|+x3,则f(lg 2)++f(lg 5)+=( )
A.2 B.4 C.6 D.8
3.如果,那么下列关系式成立的是( )
A. B.
C. D.
4.在下列幂函数中,是偶函数且在上是严格增函数的是( ).
A. B. C. D.
5.图中为三个幂函数在第一象限内的图象,则解析式中指数a的值依次可以是( )
A.0.5,3, B.,3,0.5 C.0.5,,3 D.,0.5,3
6.已知碳14半衰期为5730年(注:半衰期为放射性元素残留量降为原来的一半所需要的时间),若1单位的碳14经过x年后剩余量为y单位,则y关于x的函数表达式是( )
A. B. C. D.
7.已知函数,,若,,对任意的,总存在,使得,则实数b的取值范围是( )
A.[1,7] B.[5,9] C.[4,6] D.[5,7]
8.已知函数的值域为R,则实数a的取值范围是( )
A. B. C. D.
二、多选题
9.已知a,b>0且a≠1,b≠1,若>1,则( )
A.(a-1)(a-b)<0 B.(a-1)(a-b)>0
C.(b-1)(b-a)<0 D.(b-1)(b-a)>0
10.(多选)在同一直角坐标系中,函数(a>0且a≠1)的图象可能是( )
A. B.
C. D.
11.设函数=ln(x2-x+1),则下列命题中正确的是( )
A.函数的定义域为R
B.函数是增函数
C.函数的值域为R
D.函数的图象关于直线x=对称
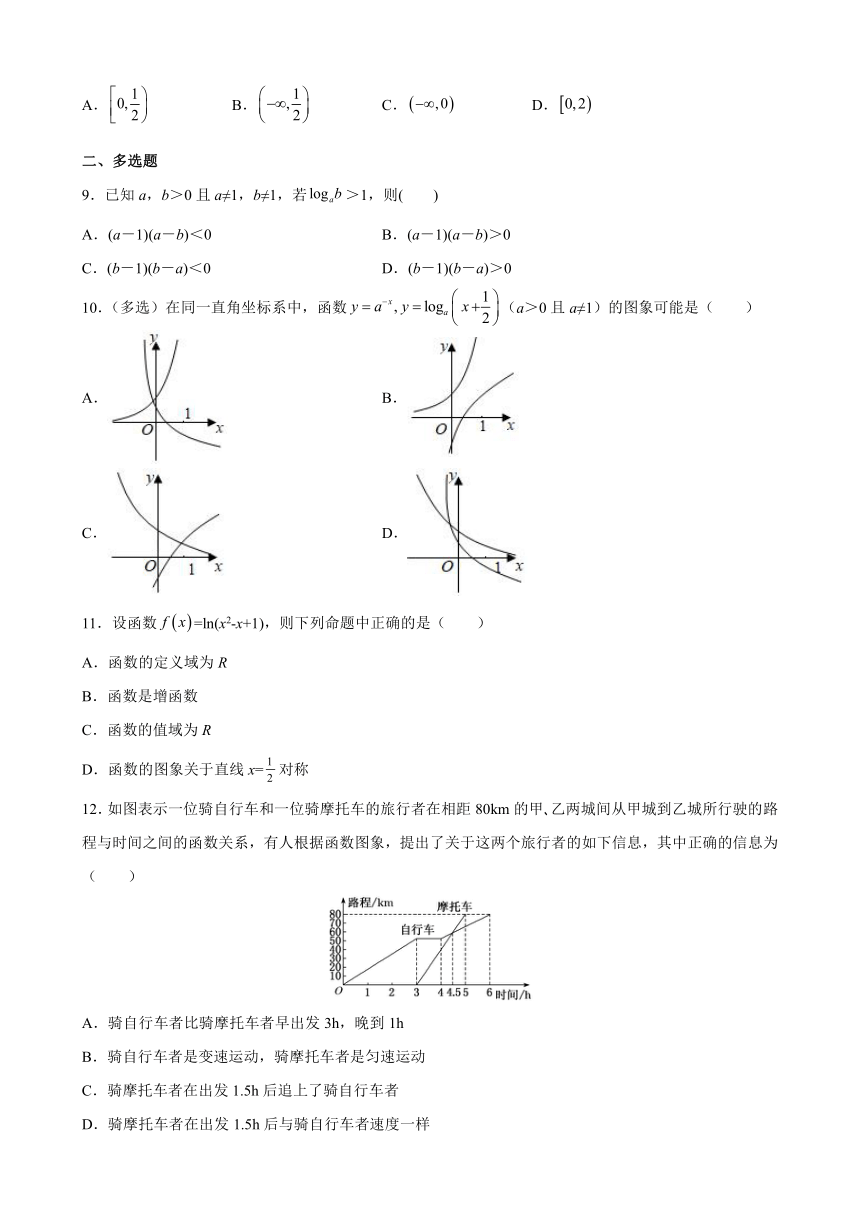
12.如图表示一位骑自行车和一位骑摩托车的旅行者在相距80km的甲 乙两城间从甲城到乙城所行驶的路程与时间之间的函数关系,有人根据函数图象,提出了关于这两个旅行者的如下信息,其中正确的信息为( )
A.骑自行车者比骑摩托车者早出发3h,晚到1h
B.骑自行车者是变速运动,骑摩托车者是匀速运动
C.骑摩托车者在出发1.5h后追上了骑自行车者
D.骑摩托车者在出发1.5h后与骑自行车者速度一样
三、填空题
13.化简:________.
14.已知、是的两个实根,则的值为______.
15.计算:______.(其中n为正整数).
16.已知函数满足,当时,函数,则__________.
四、解答题
17.用、、、、(其中,且)表示下列各式:
(1);(2);(3);(4).
设,,试比较a、b的大小关系.
19.芦荟是一种经济价值很高的观赏、食用植物,不仅可以美化居室、净化空气,又可以美容保健,因此深受人们欢迎,在国内占有很大的市场,某人准备进入芦荟市场栽培芦荟,为了解行情,进行市场调研,从4月1日起,芦荟的种植成本Q(单位:元/10kg)与上市时间t(单位:天)的数据情况如下表:
上市时间(t) 50 110 250
种植成本(Q) 150 108 150
(1)根据上表数据,从下列函数中选取一个最能反映芦荟种植成本Q与上市时间t的变化关系并求出函数关系式.;;;.
(2)利用你得到的函数关系式,求芦荟种植成本最低时上市天数t及最低种植成本.
20.设函数,且.
(1)求的值;
(2)若令,求实数t的取值范围;
(3)将表示成以为自变量的函数,并由此求函数的最大值与最小值及与之对应的x的值.
21.已知函数,当时,不等式的解集为.
(1)求,的值;
(2)若函数,求不等式的解集.
22.已知函数(且)是定义域为的奇函数,且.
(1)求的值,并判断的单调性(不要求证明);
(2)是否存在实数,使函数在上的最大值为0?如果存在,求出实数所有的值;如果不存在,请说明理由.
参考答案
1.A
【解析】A,则,故A正确;
B,则,故B错误;
C,则,故C错误;
D,若,则,即,
若,则,即,
若,则,即,故D错误;
故选:A.
2.A
【解析】由于f(x)=|x|+x3,得f(-x)+f(x)=2|x|,
又lg =-lg 2,lg =-lg 5.
∴原式=2|lg 2|+2|lg 5|=2(lg 2+lg 5)=2.
故选:A﹒
3.C
【解析】因为,所以,所以
故选:C
4.D
【解析】函数为偶函数,在上是严格减函数,A错,
函数不是偶函数,在上是严格减函数,B错,
函数是奇函数,在上是严格增函数,C错,
函数是偶函数,在上是严格增函数,D对,
故选:D.
5.D
【解析】解:由幂函数在第一象限内的图象知,
图中对应的,对应的,对应的,
所以,解析式中指数a的值依次可以是,和3.
故选:D.
6.A
【解析】设1单位的碳14经过1年后剩余量为a单位,则经过x年后剩余量为,
根据半衰期的定义可得,当时,,
所以,所以,
所以.
故选:A.
7.D
【解析】函数在[1,3]上单调递增,所以.函数的图象开口向下,对称轴为直线,所以g(x)在[1,3]上单调递减,所以.因为对任意的,总存在,使得,所以,所以,解得.
故选:D
8.A
【解析】因为在上单调递增,
所以当时,,
若函数的值域为R,
则,
解得.
故选:A.
9.AD
【解析】①当a>1时,>1=,∴b>a,∴b>a>1,∴(a-1)(a-b)<0;
②当0<a<1时,>1=,∴b<a,∴0<b<a<1,∴b-1<0,b-a<0,∴(b-1)(b-a)>0.
故选:AD﹒
10.AC
【解析】由函数,
当a>1时,可得是递减函数,图象恒过(0,1)点,
函数,是递增函数,图象恒过,
当1>a>0时,可得是递增函数,图象恒过(0,1)点,
函数,是递减函数,图象恒过;
∴满足要求的图象为:A,C
故选:AC
11.AD
【解析】A正确,∵x2-x+1=>0恒成立,∴函数的定义域为R;
B错误,函数y=ln(x2-x+1)在x>时是增函数,在x<时是减函数;
C错误,由x2-x+1=可得y=ln(x2-x+1)≥,∴函数的值域为;
D正确,,故函数的图象关于直线x=对称.
故选:.
【点睛】
本题考查对数型复合函数性质的求解,属综合基础题.
12.ABC
【解析】由时间轴上,自行车、摩托车对应函数的起止点所对应的时间值,知A正确;骑摩托车者行驶的路程与时间的函数图象是线段,所以是匀速运动,而骑自行车者行驶的路程与时间的函数图象是折线段,所以是变速运动, B正确;两条曲线的交点的横坐标对应着4.5,结合图象知C正确;由C知,骑摩托车者在出发1.5h后即4.5h时追上自行车,而它们的车速不同,D错误
故答案选:ABC
13.
【解析】原式
故答案为:﹒
14.
【解析】因为、是的两个实根,所以,
所以
故答案为:
15.
【解析】
故答案为:.
16.
【解析】解:由题意,函数满足,化简可得,
所以函数是以2为周期的周期函数,
又由时,函数,且,
则
.
故答案为:.
17.
(1)
(2)
(3)
(4)
18..
【解析】构造函数:令,则,,
因为,又在R上是严格增函数,
所以在R上是严格减函数,在R上也是严格减函数,
因此,即.
19.
(1)应选择二次函数;
(2)当芦荟上市时间为150天时,种植成本最低为100元/10kg
(1)
由题表提供的数据知,反映芦荟种植成本Q与上市时间t的变化关系不可能是常数函数,故用所给四个函数中任意一个来反映时都应有,而函数,,均为单调函数,这与题表所给数据不符合,所以应选择二次函数.
将表中数据代入,
可得解得
所以,芦荟种植成本Q与上市时间t之间的关系式为.
(2)
当(天)时,,
即当芦荟上市时间为150天时,种植成本最低为100元/10kg.
20.(1)6;(2);(3),此时;,此时.
【解析】(1);
(2),又,,,所以t的取值范围为;
(3)由,
令,,
当时,,即,解得,
所以
,此时;
当时,,即,
,此时.
21.(1),;(2).
【解析】(1)当时,不等式的解集为
所以
解得:,
故所求函数解析式为
(2)由(1)得
,即,
且,
化简得:且,
,不等式的解集为
22.(1);为上的增函数;(2)存在,.
【解析】(1)∵函数(且)是定义域为的奇函数,,
∴,,∴.
因为,∴,,或,
∵,∴,,
因为为增函数,为减函数,所以为上的增函数.
(Ⅱ)
,
设,则,
∵,∴,记,
(1)当,即时,要使最大值为0,则要,
∵,,,∴在上单调递增,∴,由,得,因,所以满足题意.
(2)当,即时,要使最大值为0,则要,且.
∵,
①若 ,则,,
又,∴,由于,∴不合题意.
②若 ,即,则,,
综上所述,只存在满足题意.
一、单选题
1.若,,则下列关系式中正确的是( )
A. B.
C. D.
2.若函数f(x)=|x|+x3,则f(lg 2)++f(lg 5)+=( )
A.2 B.4 C.6 D.8
3.如果,那么下列关系式成立的是( )
A. B.
C. D.
4.在下列幂函数中,是偶函数且在上是严格增函数的是( ).
A. B. C. D.
5.图中为三个幂函数在第一象限内的图象,则解析式中指数a的值依次可以是( )
A.0.5,3, B.,3,0.5 C.0.5,,3 D.,0.5,3
6.已知碳14半衰期为5730年(注:半衰期为放射性元素残留量降为原来的一半所需要的时间),若1单位的碳14经过x年后剩余量为y单位,则y关于x的函数表达式是( )
A. B. C. D.
7.已知函数,,若,,对任意的,总存在,使得,则实数b的取值范围是( )
A.[1,7] B.[5,9] C.[4,6] D.[5,7]
8.已知函数的值域为R,则实数a的取值范围是( )
A. B. C. D.
二、多选题
9.已知a,b>0且a≠1,b≠1,若>1,则( )
A.(a-1)(a-b)<0 B.(a-1)(a-b)>0
C.(b-1)(b-a)<0 D.(b-1)(b-a)>0
10.(多选)在同一直角坐标系中,函数(a>0且a≠1)的图象可能是( )
A. B.
C. D.
11.设函数=ln(x2-x+1),则下列命题中正确的是( )
A.函数的定义域为R
B.函数是增函数
C.函数的值域为R
D.函数的图象关于直线x=对称
12.如图表示一位骑自行车和一位骑摩托车的旅行者在相距80km的甲 乙两城间从甲城到乙城所行驶的路程与时间之间的函数关系,有人根据函数图象,提出了关于这两个旅行者的如下信息,其中正确的信息为( )
A.骑自行车者比骑摩托车者早出发3h,晚到1h
B.骑自行车者是变速运动,骑摩托车者是匀速运动
C.骑摩托车者在出发1.5h后追上了骑自行车者
D.骑摩托车者在出发1.5h后与骑自行车者速度一样
三、填空题
13.化简:________.
14.已知、是的两个实根,则的值为______.
15.计算:______.(其中n为正整数).
16.已知函数满足,当时,函数,则__________.
四、解答题
17.用、、、、(其中,且)表示下列各式:
(1);(2);(3);(4).
设,,试比较a、b的大小关系.
19.芦荟是一种经济价值很高的观赏、食用植物,不仅可以美化居室、净化空气,又可以美容保健,因此深受人们欢迎,在国内占有很大的市场,某人准备进入芦荟市场栽培芦荟,为了解行情,进行市场调研,从4月1日起,芦荟的种植成本Q(单位:元/10kg)与上市时间t(单位:天)的数据情况如下表:
上市时间(t) 50 110 250
种植成本(Q) 150 108 150
(1)根据上表数据,从下列函数中选取一个最能反映芦荟种植成本Q与上市时间t的变化关系并求出函数关系式.;;;.
(2)利用你得到的函数关系式,求芦荟种植成本最低时上市天数t及最低种植成本.
20.设函数,且.
(1)求的值;
(2)若令,求实数t的取值范围;
(3)将表示成以为自变量的函数,并由此求函数的最大值与最小值及与之对应的x的值.
21.已知函数,当时,不等式的解集为.
(1)求,的值;
(2)若函数,求不等式的解集.
22.已知函数(且)是定义域为的奇函数,且.
(1)求的值,并判断的单调性(不要求证明);
(2)是否存在实数,使函数在上的最大值为0?如果存在,求出实数所有的值;如果不存在,请说明理由.
参考答案
1.A
【解析】A,则,故A正确;
B,则,故B错误;
C,则,故C错误;
D,若,则,即,
若,则,即,
若,则,即,故D错误;
故选:A.
2.A
【解析】由于f(x)=|x|+x3,得f(-x)+f(x)=2|x|,
又lg =-lg 2,lg =-lg 5.
∴原式=2|lg 2|+2|lg 5|=2(lg 2+lg 5)=2.
故选:A﹒
3.C
【解析】因为,所以,所以
故选:C
4.D
【解析】函数为偶函数,在上是严格减函数,A错,
函数不是偶函数,在上是严格减函数,B错,
函数是奇函数,在上是严格增函数,C错,
函数是偶函数,在上是严格增函数,D对,
故选:D.
5.D
【解析】解:由幂函数在第一象限内的图象知,
图中对应的,对应的,对应的,
所以,解析式中指数a的值依次可以是,和3.
故选:D.
6.A
【解析】设1单位的碳14经过1年后剩余量为a单位,则经过x年后剩余量为,
根据半衰期的定义可得,当时,,
所以,所以,
所以.
故选:A.
7.D
【解析】函数在[1,3]上单调递增,所以.函数的图象开口向下,对称轴为直线,所以g(x)在[1,3]上单调递减,所以.因为对任意的,总存在,使得,所以,所以,解得.
故选:D
8.A
【解析】因为在上单调递增,
所以当时,,
若函数的值域为R,
则,
解得.
故选:A.
9.AD
【解析】①当a>1时,>1=,∴b>a,∴b>a>1,∴(a-1)(a-b)<0;
②当0<a<1时,>1=,∴b<a,∴0<b<a<1,∴b-1<0,b-a<0,∴(b-1)(b-a)>0.
故选:AD﹒
10.AC
【解析】由函数,
当a>1时,可得是递减函数,图象恒过(0,1)点,
函数,是递增函数,图象恒过,
当1>a>0时,可得是递增函数,图象恒过(0,1)点,
函数,是递减函数,图象恒过;
∴满足要求的图象为:A,C
故选:AC
11.AD
【解析】A正确,∵x2-x+1=>0恒成立,∴函数的定义域为R;
B错误,函数y=ln(x2-x+1)在x>时是增函数,在x<时是减函数;
C错误,由x2-x+1=可得y=ln(x2-x+1)≥,∴函数的值域为;
D正确,,故函数的图象关于直线x=对称.
故选:.
【点睛】
本题考查对数型复合函数性质的求解,属综合基础题.
12.ABC
【解析】由时间轴上,自行车、摩托车对应函数的起止点所对应的时间值,知A正确;骑摩托车者行驶的路程与时间的函数图象是线段,所以是匀速运动,而骑自行车者行驶的路程与时间的函数图象是折线段,所以是变速运动, B正确;两条曲线的交点的横坐标对应着4.5,结合图象知C正确;由C知,骑摩托车者在出发1.5h后即4.5h时追上自行车,而它们的车速不同,D错误
故答案选:ABC
13.
【解析】原式
故答案为:﹒
14.
【解析】因为、是的两个实根,所以,
所以
故答案为:
15.
【解析】
故答案为:.
16.
【解析】解:由题意,函数满足,化简可得,
所以函数是以2为周期的周期函数,
又由时,函数,且,
则
.
故答案为:.
17.
(1)
(2)
(3)
(4)
18..
【解析】构造函数:令,则,,
因为,又在R上是严格增函数,
所以在R上是严格减函数,在R上也是严格减函数,
因此,即.
19.
(1)应选择二次函数;
(2)当芦荟上市时间为150天时,种植成本最低为100元/10kg
(1)
由题表提供的数据知,反映芦荟种植成本Q与上市时间t的变化关系不可能是常数函数,故用所给四个函数中任意一个来反映时都应有,而函数,,均为单调函数,这与题表所给数据不符合,所以应选择二次函数.
将表中数据代入,
可得解得
所以,芦荟种植成本Q与上市时间t之间的关系式为.
(2)
当(天)时,,
即当芦荟上市时间为150天时,种植成本最低为100元/10kg.
20.(1)6;(2);(3),此时;,此时.
【解析】(1);
(2),又,,,所以t的取值范围为;
(3)由,
令,,
当时,,即,解得,
所以
,此时;
当时,,即,
,此时.
21.(1),;(2).
【解析】(1)当时,不等式的解集为
所以
解得:,
故所求函数解析式为
(2)由(1)得
,即,
且,
化简得:且,
,不等式的解集为
22.(1);为上的增函数;(2)存在,.
【解析】(1)∵函数(且)是定义域为的奇函数,,
∴,,∴.
因为,∴,,或,
∵,∴,,
因为为增函数,为减函数,所以为上的增函数.
(Ⅱ)
,
设,则,
∵,∴,记,
(1)当,即时,要使最大值为0,则要,
∵,,,∴在上单调递增,∴,由,得,因,所以满足题意.
(2)当,即时,要使最大值为0,则要,且.
∵,
①若 ,则,,
又,∴,由于,∴不合题意.
②若 ,即,则,,
综上所述,只存在满足题意.
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
