2021-2022学年高一上学期数学人教A版(2019)必修第一册期末复习分类第二章 一元二次函数、方程和不等式 突破训练(Word含答案解析)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册期末复习分类第二章 一元二次函数、方程和不等式 突破训练(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 925.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 14:36:30 | ||
图片预览




文档简介
2021-2022高一数学期末复习分类突破训练——一元二次函数、方程和不等式
一、不等式和不等式性质
☆根据不等式性质和条件判断大小
1.(2021·湖南·长沙市明德中学高一期中)如果,那么下列不等式中,一定成立的是( )
A. B. C. D.
2.(2020·河北·衡水市冀州区第一中学期中)已知,,满足,且,那么下列各式中不成立的是( )
A. B. C. D.
☆作差法或作商法比较大小
1.(2021·全国·高一课时练习)已知、,设,,则与的大小关系为( )
A. B. C. D.不确定
2.(多选)(2021·福建·福州三中高三阶段练习)已知,,则下列不等式一定成立的是( )
A. B. C. D.
☆不等式的证明与范围问题
1.(2021·河南南阳·高一阶段练习)的一个充分条件是( )
A.或 B.且 C.且 D.或
2.(多选)(2021·黑龙江·哈尔滨三中高一阶段练习)已知,则下列选项正确的有( )
A. B. C. D.
二、基本不等式
☆基本不等式的内容
1.(2021·全国·高一课时练习)三国时期赵爽 在《勾股方圆图注》中对勾股定理的证明可用现代数学表述为如图所示,我们可用该图证明( )
A.如果,,那么
B.如果,那么
C.对任意正实数a和b,,当且仅当时,等号成立
D.如果,那么
2.(多选)(2021·新疆·乌苏市第一中学高一期中)已知,且.则下列不等式恒成立的是( )
A. B.
C. D.
☆拼凑法求最值
1.(2021·上海奉贤区致远高级中学高一期中)已知,当取到最小值时,的值为__________.
2.(2021·山东·胶州市教育体育局教学研究室高一期中)已知,则的最大值为______.
☆常数代换法
1.(2021·重庆十八中两江实验中学高一期中)已知,则的最小值为( )
A.6 B.5 C. D.
2.(2021·浙江·海亮高级中学高一期中)已知,且,则的最小值为( )
A. B. C. D.
☆商式最值问题
1.(2021·安徽·合肥市第六中学高一阶段练习)函数()的最小值为( )
A. B. C. D.
2.(2021·江苏·常州市北郊高级中学高一阶段练习)已知,且,则最大值为______.
☆基本不等式参数问题与应用
1.(2021·河南驻马店·高三阶段练习(理))若对任意恒成立,则实数的取值范围是( )
A. B. C. D.
2.(2021·江苏张家港·高一期中)一家货物公司计划租地建造仓库储存货物,经过市场调查了解到下列信息:每月土地占地费(单位:万元)与仓库到车站的距离(单位:km)成反比,每月库存货物费(单位:万元)与成正比;若在距离车站10km处建仓库,则与分别为2万元和8.2万元.记两项费用之和为.
(1)求关于的解析式;
(2)这家公司应该把仓库建在距离车站多少千米处,才能使两项费用之和最小?求出最小值.
三、二次函数、一元二次方程、不等式
☆一元二次不等式的解法
1.(2021·福建省长乐第七中学高三期中)不等式的解集是( ).
A. B. C.或 D.
2.(2021·全国·高一课时练习)与不等式同解的不等式是( )
A. B.
C. D.
☆含参数的一元二次不等式
·.(2021·全国·高一课时练习)关于x的不等式()的解集为( )
A.或 B.
C.或 D.
2.(多选)(2021·山东肥城·高一期中)已知关于的不等式的解集为,下列说法正确的是( )
A.
B.
C.不等式的解集为
D.不等式的解集为
☆一元二次不等式恒成立问题
1.(2020·湖南·嘉禾县第一中学高一阶段练习)若不等式对恒成立,则a的取值范围为( )
A. B.
C. D.
2.(2021·广东·高一期中)若不等式在上恒成立.则实数a的取值范围是______.
☆一元二次不等式的应用
1.(2021·云南·玉溪市江川区第二中学高一期中)北京、张家港2022年冬奥会申办委员会在俄罗斯索契举办了发布会,某公司为了竞标配套活动的相关代言,决定对旗下的某商品进行一次评估.该商品原来每件售价为元,年销售万件.据市场调査,若价格每提高元,销售量将相应减少件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
巩固提升
一、单选题
1.设,,则有( )
A. B. C. D.
2.不等式的解集为( )
A. B.或 C.或 D.
3.若,都为正实数,,则的最大值是( )
A. B. C. D.
4.一元二次不等式的解集是,则的解集是( )
A. B.
C. D.
5.若,则的最大值是( )
A. B. C. D.
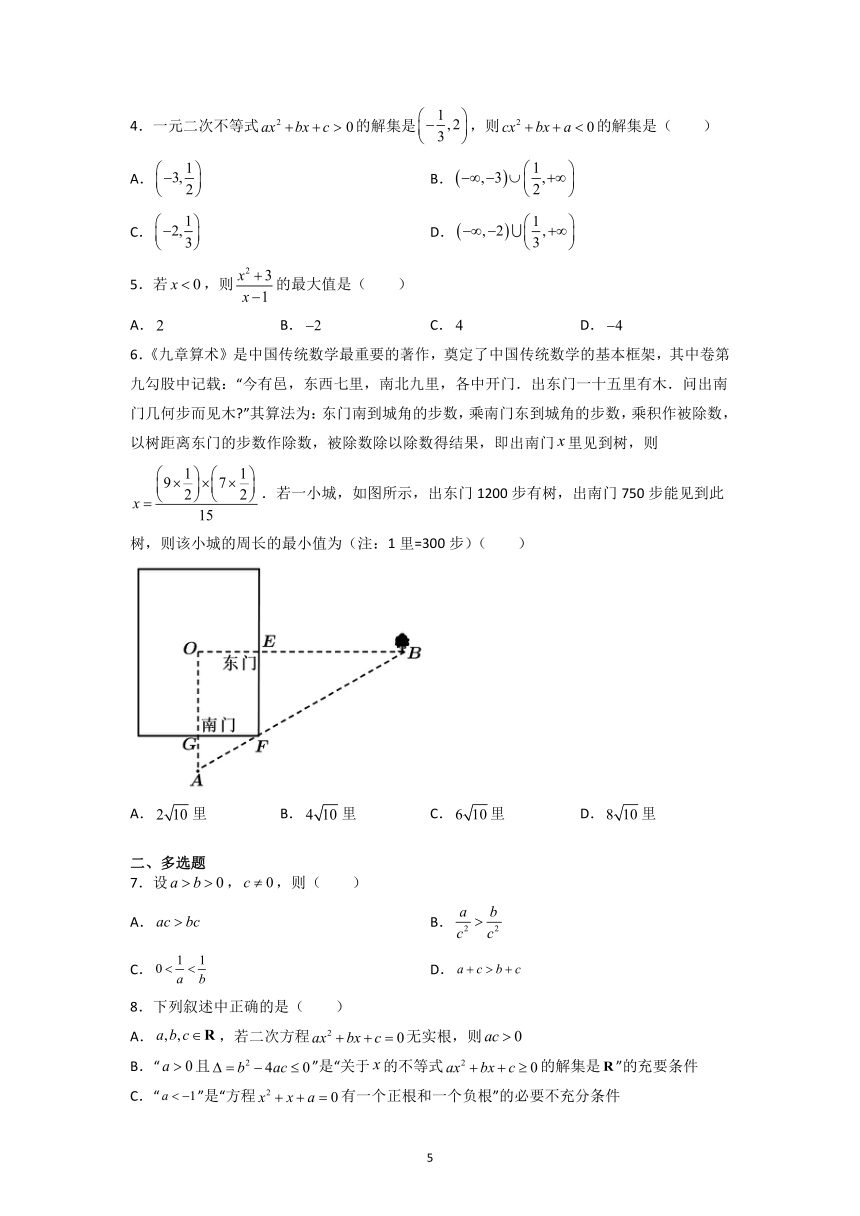
6.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,其中卷第九勾股中记载:“今有邑,东西七里,南北九里,各中开门.出东门一十五里有木.问出南门几何步而见木 ”其算法为:东门南到城角的步数,乘南门东到城角的步数,乘积作被除数,以树距离东门的步数作除数,被除数除以除数得结果,即出南门里见到树,则.若一小城,如图所示,出东门1200步有树,出南门750步能见到此树,则该小城的周长的最小值为(注:1里=300步)( )
A.里 B.里 C.里 D.里
二、多选题
7.设,,则( )
A. B.
C. D.
8.下列叙述中正确的是( )
A.,若二次方程无实根,则
B.“且”是“关于的不等式的解集是”的充要条件
C.“”是“方程有一个正根和一个负根”的必要不充分条件
D.“”是“”的充分不必要条件
9.已知,,则下列选项一定正确的是( )
A.
B.的最大值为
C.的最大值为2
D.
三、填空题
10.设,,则x-y的取值范围是______.
11.要制作一个容积为,高为的无盖长方形容器,已知该容器的底面造价是每平方米40元,侧面造价是每平方米20元,则该容器的最低总造价是______元.
12.设,为实数,若对于满足的全体,,不等式恒成立,则实数的取值范围是________.
四、解答题
13.(1)设,证明:.
(2)已知正实数满足,求证:.
14.某厂家拟在年举行某产品的促销活动,经调查,该产品的年销售量(即该产品的年产量)(单位:万件)与年促销费(单位:万元)满足(为常数),如果不举行促销活动,该产品的年销售量是万件,已知年生产该产品的固定投入为万元,每生产万件该产品需要再投入万元,厂家将每件产品的销售价格定为每件产品年平均成本的倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
(1)将年该产品的利润(单位:万元)表示为年促销费用的函数;
(2)该厂家年的促销费用为多少万元时,厂家的利润最大?
15.已知.
(1)若不等式的解集为,求实数、的值;
(2)若时,对于任意的实数,都有,求的取值范围.
参考答案
一、不等式和不等式性质
☆根据不等式性质和条件判断大小
1.D
若,则由可得,,,
因为,,所以.
故选:D
2.A
因为,且,所以
所以,故A不成立
,,,故BCD成立
故选:A
☆作差法或作商法比较大小
1.B
解析:.
因为、,所以,,,所以,所以.
故选:B.
2.BC
对于A项:因为,所以,又,所以,A错;
对于B项:因为,所以,B对;
对于C项:,因为,,所以,又因为,所以,C对;
对于D项:,所以,D错.
故选:BC.
☆不等式的证明与范围问题
1.C
选项A,取,满足或,但,故充分性不成立;
选项B,取,满足且,但,故充分性不成立;
选项C,由不等式的性质,且能推出,故充分性成立
选项D,取,满足或,但,故充分性不成立;
故选:C
2.AD
因为,所以,故,故A正确;
因为,所以,因此,故B错误;
因为,所以,因此,故C错误;
因为,所以,故D正确,
故选:AD.
二、基本不等式
☆基本不等式的内容
1.C
可将直角三角形的两直角边记作a,b,
斜边长为c(,),
则外围的正方形的面积为,也就是.
四个直角三角形所在的阴影面积之和刚好为2ab.
故对任意正实数a和b,有,
当且仅当时,等号成立.
故选:C
2.AC
当时,,所以BD选项错误.
A,,当且仅当时,等号成立,A正确.
C,,,当且仅当时,等号成立,C正确.
故选:AC
☆拼凑法求最值
1.3
解:因为.
由题得.
当且仅当时等号成立.
故答案为:3
2.
当且仅当,即时等号成立
故答案为:
☆常数代换法
1.D
因为,所以,
所以
,
当且仅当即时等号成立,
所以的最小值为,
故选:D.
2.C
由,得:,且,当且仅当,即时等号成立.
故选:C
☆商式最值问题
1.B
解:因为,所以,
所以,
当且仅当,即时取等号,
所以函数()的最小值为,
故选:B
2.
解:由且,可得,代入,
又,
当且仅当,即,
又,可得,时,不等式取等,
即的最大值为,
故答案为:.
☆基本不等式参数问题与应用
1.B
由题意,对任意有
当且仅当,即时,等号成立,即的最大值为﹒
又由对任意时,恒成立,,即的取值范围是.
故选:B.
2.
(1)
(2)这家公司应该把仓库建在距离车站5千米处,才能使两项费用之和最小,最小值为8.2万元
(1)
∵每月土地占地费y1(单位:万元)与仓库到车站的距离x(单位:km)成反比,
∴可设,
∵每月库存货物费y2(单位:万元)与(4x+1)成正比,
∴可设y2=(4x+1)k2,
又∵在距离车站10km处建仓库,则y1与y2分别为2万元和8.2万元,
∴k1=2×10=20,,
∴,y2=(4x+1)×0.2=0.8x+0.2,
∴w=y1+y2= (x>0).
(2)
∵≥,当且仅当,即x=5时等号成立,
∴这家公司应该把仓库建在距离车站5千米处,才能使两项费用之和最小,最小值为8.2万元.
三、二次函数、一元二次方程、不等式
☆一元二次不等式的解法
1.A
由题意知,,所以原不等式的解集为.
故选:A.
2.B
,即,解得,
A项:,解得,不正确;
B项:,解得,正确;
C项:,即,解得,不正确;
D项:,解得,不正确,
☆含参数的一元二次不等式
1.D
根据题意,由,得,
∵,∴.
故选:D.
2.ABD
因为关于的不等式解集为,
所以和是方程的两个实根,且,故A正确;
所以,,所以,
因为,又,所以,故B正确;
不等式可化为,因为,所以,故C错误;
不等式可化为,又,
所以,即,解得,故D正确.
故选:ABD.
☆一元二次不等式恒成立问题
1.A
当时,原不等式即为,不合题意,
∴,故,解得.
故选:A.
2.
设,
若,在上单调递减,而,所以满足题意;
若,不满足题意;
若,函数的对称轴,所以在上为减函数,
而,所以满足题意.
综上,a的取值范围是.
故答案为:
☆一元二次不等式的应用
1.每件定价最多为元.
设每件定价为元,依题意得,整理得
,解得:.
所以要使销售的总收入不低于原收入,每件定价最多为元.
巩固提升
1.A
解:∵,
∴,
故选:A.
2.C
由得,即,
解得或.
故原不等式的解集为或.
故选:C.
3.D
因为,都为正实数,,
所以,
当且仅当,即时,取最大值.
故选:D
4.A
因为一元二次不等式的解集是,
所以,即,且,
所以不等式为,即,,.
故选:A.
5.B
因为,所以
,
当且仅当,即时,等号成立,
故选:B.
6.D
因为1里=300步,
则由图知步=4里,步=2.5里.
由题意,得,
则,
所以该小城的周长为,
当且仅当时等号成立.
故选:D.
7.BCD
解:A. ,当时,不等式不成立,所以该选项错误;
B. ,根据不等式的性质可判断该选项正确;
C. 根据不等式的性质得到,所以该选项正确;
D. 根据不等式的性质得到,所以该选项正确.
故选:BCD
8.AD
二次方程无实根,则,所以,故,A正确;关于的不等式的解集是,则当,时,满足题意,当且时,也满足题意,故“且”是“关于的不等式的解集是”的充分不必要条件,B错误;方程有一个正根和一个负根,则要满足,解得:,因为,但,故是“方程有一个正根和一个负根”的充分不必要条件,C错误;,解得:或,因为或,但或
故“”是“”的充分不必要条件,D选项正确
故选:AD
9.BD
,,,,
对于A,因为,所以,
当且仅当,即时等号成立,故A错误;
对于B, 因为,所以,当且仅当,即时等号成立,故B正确;
对于C,因为,所以,,,即,故C错误;
对于D,,当且仅当,即,时等号成立,,故D正确
故选:BD
10.
由,得,
因为,
所以,即,
故答案为:
11.320
设池底长和宽分别为am,bm,成本为y元.
∵长方形容器的容器为4m3,高为1m,故底面面积,
∴.
∵,故当时,y取最小值320,即该容器的最低总造价是320元.
故答案为:320.
12.或
∵,
∴,
∴,当且仅当取等号,
∴,又不等式恒成立,
∴,解得或.
故答案为:或.
13.(1)证明见解析;(2)证明见解析.
证明:(1)
,
又,
而,
故,即.
(2)∵正数满足,
,
,当且仅当时取等号,
.
14.(1);(2)促销费用投入万元时,厂家的利润最大.
(1)由题意可知:当时,(万件),,解得:,
,又每件产品的销售价格为,
年利润,
(2)当时,(当且仅当,即时取等号),
此时年利润(万元);
该厂家年的促销费用投入万元时,厂家的利润最大,最大为万元.
15.(1);(2).
(1)因为的解集为,,
所以方程的两根为、,
故,解得,
经检验:当、时,不等式的解集为.
(2)当时,,
对于任意的实数,都有,
即对于任意的实数,都有,
令,
当时,恒成立;
当时,函数是增函数,即,解得;
当时,函数是减函数,即,解得,
综上所述,,的取值范围为.
一、不等式和不等式性质
☆根据不等式性质和条件判断大小
1.(2021·湖南·长沙市明德中学高一期中)如果,那么下列不等式中,一定成立的是( )
A. B. C. D.
2.(2020·河北·衡水市冀州区第一中学期中)已知,,满足,且,那么下列各式中不成立的是( )
A. B. C. D.
☆作差法或作商法比较大小
1.(2021·全国·高一课时练习)已知、,设,,则与的大小关系为( )
A. B. C. D.不确定
2.(多选)(2021·福建·福州三中高三阶段练习)已知,,则下列不等式一定成立的是( )
A. B. C. D.
☆不等式的证明与范围问题
1.(2021·河南南阳·高一阶段练习)的一个充分条件是( )
A.或 B.且 C.且 D.或
2.(多选)(2021·黑龙江·哈尔滨三中高一阶段练习)已知,则下列选项正确的有( )
A. B. C. D.
二、基本不等式
☆基本不等式的内容
1.(2021·全国·高一课时练习)三国时期赵爽 在《勾股方圆图注》中对勾股定理的证明可用现代数学表述为如图所示,我们可用该图证明( )
A.如果,,那么
B.如果,那么
C.对任意正实数a和b,,当且仅当时,等号成立
D.如果,那么
2.(多选)(2021·新疆·乌苏市第一中学高一期中)已知,且.则下列不等式恒成立的是( )
A. B.
C. D.
☆拼凑法求最值
1.(2021·上海奉贤区致远高级中学高一期中)已知,当取到最小值时,的值为__________.
2.(2021·山东·胶州市教育体育局教学研究室高一期中)已知,则的最大值为______.
☆常数代换法
1.(2021·重庆十八中两江实验中学高一期中)已知,则的最小值为( )
A.6 B.5 C. D.
2.(2021·浙江·海亮高级中学高一期中)已知,且,则的最小值为( )
A. B. C. D.
☆商式最值问题
1.(2021·安徽·合肥市第六中学高一阶段练习)函数()的最小值为( )
A. B. C. D.
2.(2021·江苏·常州市北郊高级中学高一阶段练习)已知,且,则最大值为______.
☆基本不等式参数问题与应用
1.(2021·河南驻马店·高三阶段练习(理))若对任意恒成立,则实数的取值范围是( )
A. B. C. D.
2.(2021·江苏张家港·高一期中)一家货物公司计划租地建造仓库储存货物,经过市场调查了解到下列信息:每月土地占地费(单位:万元)与仓库到车站的距离(单位:km)成反比,每月库存货物费(单位:万元)与成正比;若在距离车站10km处建仓库,则与分别为2万元和8.2万元.记两项费用之和为.
(1)求关于的解析式;
(2)这家公司应该把仓库建在距离车站多少千米处,才能使两项费用之和最小?求出最小值.
三、二次函数、一元二次方程、不等式
☆一元二次不等式的解法
1.(2021·福建省长乐第七中学高三期中)不等式的解集是( ).
A. B. C.或 D.
2.(2021·全国·高一课时练习)与不等式同解的不等式是( )
A. B.
C. D.
☆含参数的一元二次不等式
·.(2021·全国·高一课时练习)关于x的不等式()的解集为( )
A.或 B.
C.或 D.
2.(多选)(2021·山东肥城·高一期中)已知关于的不等式的解集为,下列说法正确的是( )
A.
B.
C.不等式的解集为
D.不等式的解集为
☆一元二次不等式恒成立问题
1.(2020·湖南·嘉禾县第一中学高一阶段练习)若不等式对恒成立,则a的取值范围为( )
A. B.
C. D.
2.(2021·广东·高一期中)若不等式在上恒成立.则实数a的取值范围是______.
☆一元二次不等式的应用
1.(2021·云南·玉溪市江川区第二中学高一期中)北京、张家港2022年冬奥会申办委员会在俄罗斯索契举办了发布会,某公司为了竞标配套活动的相关代言,决定对旗下的某商品进行一次评估.该商品原来每件售价为元,年销售万件.据市场调査,若价格每提高元,销售量将相应减少件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
巩固提升
一、单选题
1.设,,则有( )
A. B. C. D.
2.不等式的解集为( )
A. B.或 C.或 D.
3.若,都为正实数,,则的最大值是( )
A. B. C. D.
4.一元二次不等式的解集是,则的解集是( )
A. B.
C. D.
5.若,则的最大值是( )
A. B. C. D.
6.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,其中卷第九勾股中记载:“今有邑,东西七里,南北九里,各中开门.出东门一十五里有木.问出南门几何步而见木 ”其算法为:东门南到城角的步数,乘南门东到城角的步数,乘积作被除数,以树距离东门的步数作除数,被除数除以除数得结果,即出南门里见到树,则.若一小城,如图所示,出东门1200步有树,出南门750步能见到此树,则该小城的周长的最小值为(注:1里=300步)( )
A.里 B.里 C.里 D.里
二、多选题
7.设,,则( )
A. B.
C. D.
8.下列叙述中正确的是( )
A.,若二次方程无实根,则
B.“且”是“关于的不等式的解集是”的充要条件
C.“”是“方程有一个正根和一个负根”的必要不充分条件
D.“”是“”的充分不必要条件
9.已知,,则下列选项一定正确的是( )
A.
B.的最大值为
C.的最大值为2
D.
三、填空题
10.设,,则x-y的取值范围是______.
11.要制作一个容积为,高为的无盖长方形容器,已知该容器的底面造价是每平方米40元,侧面造价是每平方米20元,则该容器的最低总造价是______元.
12.设,为实数,若对于满足的全体,,不等式恒成立,则实数的取值范围是________.
四、解答题
13.(1)设,证明:.
(2)已知正实数满足,求证:.
14.某厂家拟在年举行某产品的促销活动,经调查,该产品的年销售量(即该产品的年产量)(单位:万件)与年促销费(单位:万元)满足(为常数),如果不举行促销活动,该产品的年销售量是万件,已知年生产该产品的固定投入为万元,每生产万件该产品需要再投入万元,厂家将每件产品的销售价格定为每件产品年平均成本的倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
(1)将年该产品的利润(单位:万元)表示为年促销费用的函数;
(2)该厂家年的促销费用为多少万元时,厂家的利润最大?
15.已知.
(1)若不等式的解集为,求实数、的值;
(2)若时,对于任意的实数,都有,求的取值范围.
参考答案
一、不等式和不等式性质
☆根据不等式性质和条件判断大小
1.D
若,则由可得,,,
因为,,所以.
故选:D
2.A
因为,且,所以
所以,故A不成立
,,,故BCD成立
故选:A
☆作差法或作商法比较大小
1.B
解析:.
因为、,所以,,,所以,所以.
故选:B.
2.BC
对于A项:因为,所以,又,所以,A错;
对于B项:因为,所以,B对;
对于C项:,因为,,所以,又因为,所以,C对;
对于D项:,所以,D错.
故选:BC.
☆不等式的证明与范围问题
1.C
选项A,取,满足或,但,故充分性不成立;
选项B,取,满足且,但,故充分性不成立;
选项C,由不等式的性质,且能推出,故充分性成立
选项D,取,满足或,但,故充分性不成立;
故选:C
2.AD
因为,所以,故,故A正确;
因为,所以,因此,故B错误;
因为,所以,因此,故C错误;
因为,所以,故D正确,
故选:AD.
二、基本不等式
☆基本不等式的内容
1.C
可将直角三角形的两直角边记作a,b,
斜边长为c(,),
则外围的正方形的面积为,也就是.
四个直角三角形所在的阴影面积之和刚好为2ab.
故对任意正实数a和b,有,
当且仅当时,等号成立.
故选:C
2.AC
当时,,所以BD选项错误.
A,,当且仅当时,等号成立,A正确.
C,,,当且仅当时,等号成立,C正确.
故选:AC
☆拼凑法求最值
1.3
解:因为.
由题得.
当且仅当时等号成立.
故答案为:3
2.
当且仅当,即时等号成立
故答案为:
☆常数代换法
1.D
因为,所以,
所以
,
当且仅当即时等号成立,
所以的最小值为,
故选:D.
2.C
由,得:,且,当且仅当,即时等号成立.
故选:C
☆商式最值问题
1.B
解:因为,所以,
所以,
当且仅当,即时取等号,
所以函数()的最小值为,
故选:B
2.
解:由且,可得,代入,
又,
当且仅当,即,
又,可得,时,不等式取等,
即的最大值为,
故答案为:.
☆基本不等式参数问题与应用
1.B
由题意,对任意有
当且仅当,即时,等号成立,即的最大值为﹒
又由对任意时,恒成立,,即的取值范围是.
故选:B.
2.
(1)
(2)这家公司应该把仓库建在距离车站5千米处,才能使两项费用之和最小,最小值为8.2万元
(1)
∵每月土地占地费y1(单位:万元)与仓库到车站的距离x(单位:km)成反比,
∴可设,
∵每月库存货物费y2(单位:万元)与(4x+1)成正比,
∴可设y2=(4x+1)k2,
又∵在距离车站10km处建仓库,则y1与y2分别为2万元和8.2万元,
∴k1=2×10=20,,
∴,y2=(4x+1)×0.2=0.8x+0.2,
∴w=y1+y2= (x>0).
(2)
∵≥,当且仅当,即x=5时等号成立,
∴这家公司应该把仓库建在距离车站5千米处,才能使两项费用之和最小,最小值为8.2万元.
三、二次函数、一元二次方程、不等式
☆一元二次不等式的解法
1.A
由题意知,,所以原不等式的解集为.
故选:A.
2.B
,即,解得,
A项:,解得,不正确;
B项:,解得,正确;
C项:,即,解得,不正确;
D项:,解得,不正确,
☆含参数的一元二次不等式
1.D
根据题意,由,得,
∵,∴.
故选:D.
2.ABD
因为关于的不等式解集为,
所以和是方程的两个实根,且,故A正确;
所以,,所以,
因为,又,所以,故B正确;
不等式可化为,因为,所以,故C错误;
不等式可化为,又,
所以,即,解得,故D正确.
故选:ABD.
☆一元二次不等式恒成立问题
1.A
当时,原不等式即为,不合题意,
∴,故,解得.
故选:A.
2.
设,
若,在上单调递减,而,所以满足题意;
若,不满足题意;
若,函数的对称轴,所以在上为减函数,
而,所以满足题意.
综上,a的取值范围是.
故答案为:
☆一元二次不等式的应用
1.每件定价最多为元.
设每件定价为元,依题意得,整理得
,解得:.
所以要使销售的总收入不低于原收入,每件定价最多为元.
巩固提升
1.A
解:∵,
∴,
故选:A.
2.C
由得,即,
解得或.
故原不等式的解集为或.
故选:C.
3.D
因为,都为正实数,,
所以,
当且仅当,即时,取最大值.
故选:D
4.A
因为一元二次不等式的解集是,
所以,即,且,
所以不等式为,即,,.
故选:A.
5.B
因为,所以
,
当且仅当,即时,等号成立,
故选:B.
6.D
因为1里=300步,
则由图知步=4里,步=2.5里.
由题意,得,
则,
所以该小城的周长为,
当且仅当时等号成立.
故选:D.
7.BCD
解:A. ,当时,不等式不成立,所以该选项错误;
B. ,根据不等式的性质可判断该选项正确;
C. 根据不等式的性质得到,所以该选项正确;
D. 根据不等式的性质得到,所以该选项正确.
故选:BCD
8.AD
二次方程无实根,则,所以,故,A正确;关于的不等式的解集是,则当,时,满足题意,当且时,也满足题意,故“且”是“关于的不等式的解集是”的充分不必要条件,B错误;方程有一个正根和一个负根,则要满足,解得:,因为,但,故是“方程有一个正根和一个负根”的充分不必要条件,C错误;,解得:或,因为或,但或
故“”是“”的充分不必要条件,D选项正确
故选:AD
9.BD
,,,,
对于A,因为,所以,
当且仅当,即时等号成立,故A错误;
对于B, 因为,所以,当且仅当,即时等号成立,故B正确;
对于C,因为,所以,,,即,故C错误;
对于D,,当且仅当,即,时等号成立,,故D正确
故选:BD
10.
由,得,
因为,
所以,即,
故答案为:
11.320
设池底长和宽分别为am,bm,成本为y元.
∵长方形容器的容器为4m3,高为1m,故底面面积,
∴.
∵,故当时,y取最小值320,即该容器的最低总造价是320元.
故答案为:320.
12.或
∵,
∴,
∴,当且仅当取等号,
∴,又不等式恒成立,
∴,解得或.
故答案为:或.
13.(1)证明见解析;(2)证明见解析.
证明:(1)
,
又,
而,
故,即.
(2)∵正数满足,
,
,当且仅当时取等号,
.
14.(1);(2)促销费用投入万元时,厂家的利润最大.
(1)由题意可知:当时,(万件),,解得:,
,又每件产品的销售价格为,
年利润,
(2)当时,(当且仅当,即时取等号),
此时年利润(万元);
该厂家年的促销费用投入万元时,厂家的利润最大,最大为万元.
15.(1);(2).
(1)因为的解集为,,
所以方程的两根为、,
故,解得,
经检验:当、时,不等式的解集为.
(2)当时,,
对于任意的实数,都有,
即对于任意的实数,都有,
令,
当时,恒成立;
当时,函数是增函数,即,解得;
当时,函数是减函数,即,解得,
综上所述,,的取值范围为.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
