2021-2022学年鲁教版(五四制)七年级数学第一学期期末综合复习题2 (Word版 含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)七年级数学第一学期期末综合复习题2 (Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 258.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 08:29:48 | ||
图片预览



文档简介
2021-2022学年鲁教版七年级数学第一学期期末综合复习题2(附答案)
一、选择题(共10小题,满分30分.)
1.在π,,,0.303003,﹣中,无理数的个数是( )
A.1个 B.2个 C.3个 D.4个
2.下列在具体情境中不能确定平面内位置的是( )
A.东经37°,北纬21° B.电影院某放映厅7排3号
C.芝罘区南大街
D.烟台山灯塔北偏东60°方向,距离灯塔3千米
3.下列计算正确的是( )
A.=4 B.﹣= C.=±5 D.(﹣)2=4
4.利用全等三角形测量距离的依据是( )
A.全等三角形的对应角相等 B.全等三角形的对应边相等
C.大小和形状相同的两个三角形全等 D.三边对应相等的两个三角形全等
5.估计介于( )
A.0.4与0.5之间 B.0.5与0.6之间
C.0.6与0.7之间 D.0.7与0.8之间
6.将一副三角板按图中的方式叠放,则∠1的度数为( )
A.105° B.100° C.95° D.110°
7.直角坐标系中,若点P(a,b)在第二象限中,则点Q(﹣a,﹣b)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.如图,Rt△ABC中,∠ACB=90°,∠A=55°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( )
A.40° B.30° C.20° D.10°
9.下列说法正确的是( )
A.y=kx+b一定是一次函数
B.有的实数在数轴上找不到对应的点
C.长为,,的三条线段能组成直角三角形
D.无论x为何值,点P(﹣2,x2+1)总是在第二象限
10.A,B两地相距20km,甲乙两人沿同一条路线从A地到B地,如图的图象反映的是二人行进路程y(km)与行进时间t(h)之间的关系,有下列说法:①甲始终是匀速行进,乙的行进不是匀速的;②甲用了5个小时到达目的地;③乙比甲先出发1小时;④甲在出发4小时后被乙追上.在这些说法中,正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共10小题,满分30分.)
11.等腰三角形的一个底角为50°,则它的顶角的度数为 .
12.若一个数x的平方根是m﹣3和m﹣7,那么这个数x是 .
13.的平方根是 .
14.如果点P在第四象限内,点P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为 .
15.我们可以利用计算器求一个正数a的算术平方根,其操作方法是按顺序进行按键输入:.小明按键输入显示结果为4,则他按键输入显示结果应为 .
16.已知点A(2,﹣4),直线y=﹣x﹣2与y轴交于点B,在x轴上存在一点P,使得PA+PB的值最小,则点P的坐标为 .
17.一个正方形的面积为48平方单位,它的边长在两个相邻整数之间,这两个整数是 .
18.一个正方体的体积变为原来的27倍,则它的棱长变为原来的 倍.
19.如图所示,雪天路滑,为了让学生进教学楼更安全,校方特意在楼梯上铺了防滑地毯(图中虚线部分),小明同学测得∠A=30°,并且从老师那里得知地毯总长度为(300+300)厘米,那么这段楼梯的高度BC为 .
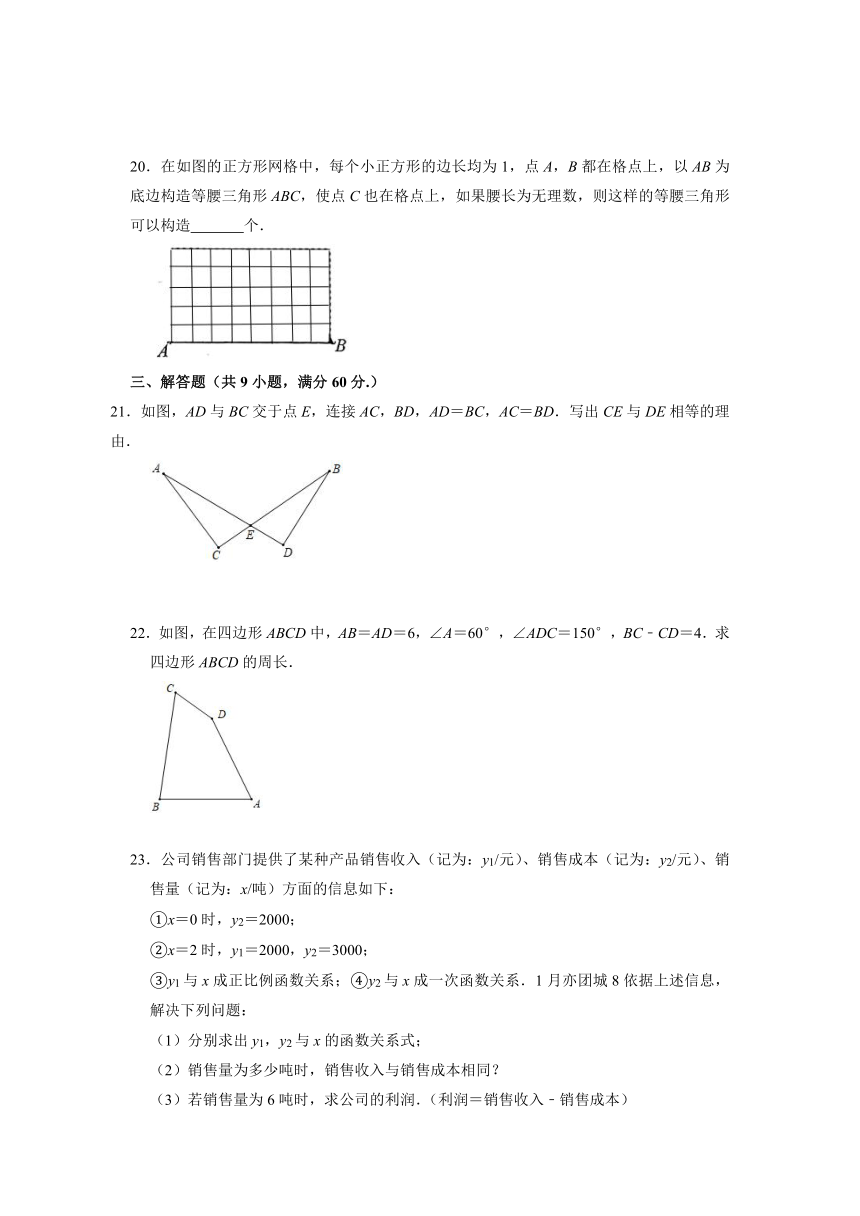
20.在如图的正方形网格中,每个小正方形的边长均为1,点A,B都在格点上,以AB为底边构造等腰三角形ABC,使点C也在格点上,如果腰长为无理数,则这样的等腰三角形可以构造 个.
解答题(共9小题,满分60分.)
21.如图,AD与BC交于点E,连接AC,BD,AD=BC,AC=BD.写出CE与DE相等的理由.
22.如图,在四边形ABCD中,AB=AD=6,∠A=60°,∠ADC=150°,BC﹣CD=4.求四边形ABCD的周长.
23.公司销售部门提供了某种产品销售收入(记为:y1/元)、销售成本(记为:y2/元)、销售量(记为:x/吨)方面的信息如下:
①x=0时,y2=2000;
②x=2时,y1=2000,y2=3000;
③y1与x成正比例函数关系;④y2与x成一次函数关系.1月亦团城8依据上述信息,解决下列问题:
(1)分别求出y1,y2与x的函数关系式;
(2)销售量为多少吨时,销售收入与销售成本相同?
(3)若销售量为6吨时,求公司的利润.(利润=销售收入﹣销售成本)
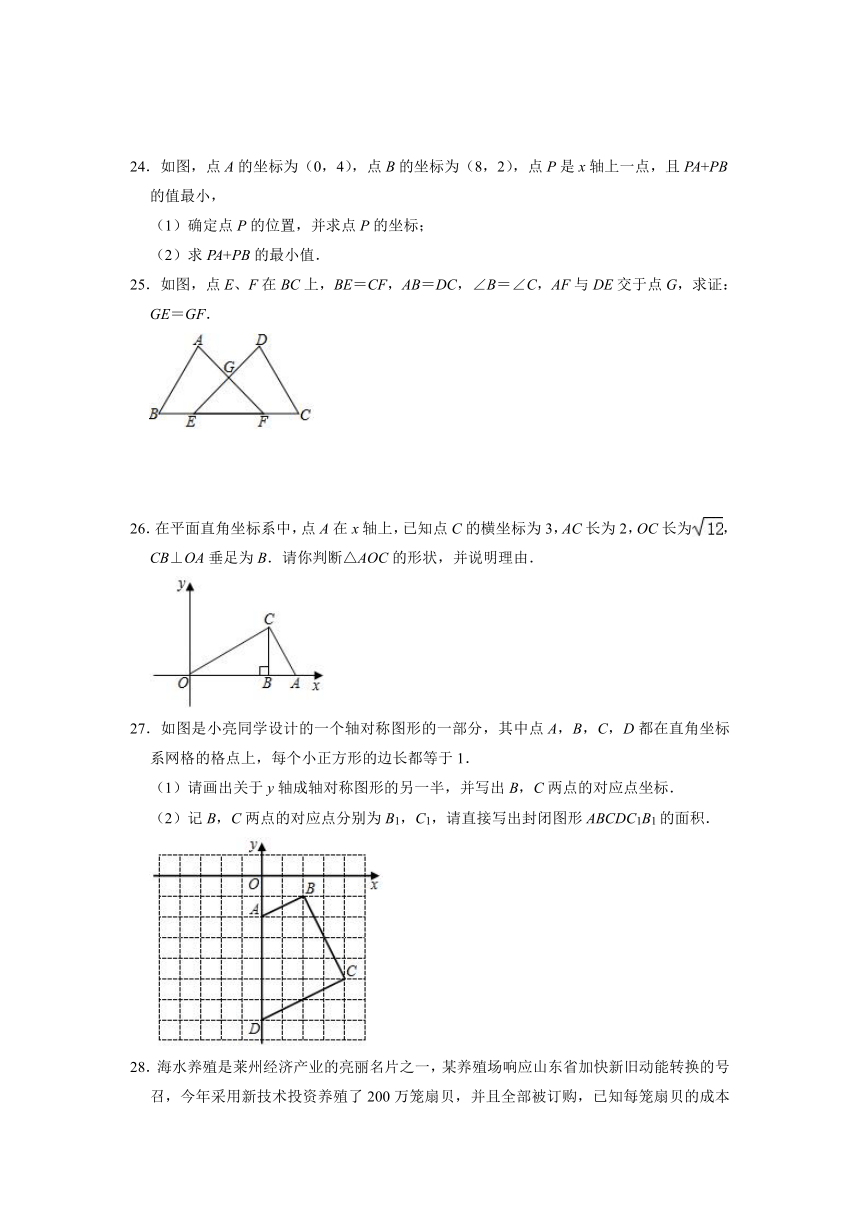
24.如图,点A的坐标为(0,4),点B的坐标为(8,2),点P是x轴上一点,且PA+PB的值最小,
(1)确定点P的位置,并求点P的坐标;
(2)求PA+PB的最小值.
25.如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:GE=GF.
26.在平面直角坐标系中,点A在x轴上,已知点C的横坐标为3,AC长为2,OC长为,CB⊥OA垂足为B.请你判断△AOC的形状,并说明理由.
27.如图是小亮同学设计的一个轴对称图形的一部分,其中点A,B,C,D都在直角坐标系网格的格点上,每个小正方形的边长都等于1.
(1)请画出关于y轴成轴对称图形的另一半,并写出B,C两点的对应点坐标.
(2)记B,C两点的对应点分别为B1,C1,请直接写出封闭图形ABCDC1B1的面积.
28.海水养殖是莱州经济产业的亮丽名片之一,某养殖场响应山东省加快新旧动能转换的号召,今年采用新技术投资养殖了200万笼扇贝,并且全部被订购,已知每笼扇贝的成本是40元,售价是100元,打捞出售过程中发现,一部分扇贝生长情况不合要求,最后只能按照25元一笼出售,如果纯收入为y万元,不合要求的扇贝有x万笼.
(1)求纯收入y关于x的关系式.
(2)当x为何值时,养殖场不赔不嫌?
29.如图,在平面直角坐标系中,直线l1:y=kx+1交y轴于点A,交x轴交于B(3,0),直线l2平行于y轴,交直线l1于点C,交x轴于点D,点D的坐标为(1,0)
(1)求直线l1的解析式和点A、C的坐标;
(2)点P是直线l2上一动点,连接PA、PB,当△ABP时以AB为直角边的直角三角形时,求点P的坐标.
参考答案:
一、选择题(共10小题,满分30分.)
1.解:,
∴在π,,,0.303003,﹣中,无理数有π,共2个.
故选:B.
2.解:A、东经37°,北纬21°物体的位置明确,故本选项错误;
B、电影院某放映厅7排3号物体的位置明确,故本选项错误;
C、芝罘区南大街无法确定物体的具体位置,故本选项正确;
D、烟台山灯塔北偏东60°方向,距离灯塔3千米物体的位置明确,故本选项错误;
故选:C.
3.解:A、=2,故此选项错误;
B、﹣,二次根式无意义,故此选项错误;
C、=5,故此选项错误;
D、(﹣)2=4,正确.
故选:D.
4.解:利用全等三角形测量距离的依据是全等三角形的对应边相等,
故选:B.
5.解:∵2.22=4.84,2.32=5.29,
∴2.2<<2.3,
∵=0.6,=0.65,
∴0.6<<0.65.
所以介于0.6与0.7之间.故选:C.
6.解:由图可知,∠2=90°﹣45°=45°,
∴∠1=180﹣45°﹣30°=105°.
故选:A.
7.解:∵点P(a,b)在第二象限中,
∴a<0,b>0,
∴﹣a>0,﹣b<0,
∴点Q(﹣a,﹣b)在第四象限,
故选:D.
8.解:在Rt△ABC中,∠ACB=90°,∠A=55°,
∴∠B=180°﹣90°﹣55°=35°,
由折叠可得:∠CA′D=∠A=55°,
又∵∠CA′D为△A′BD的外角,
∴∠CA′D=∠B+∠A′DB,
则∠A′DB=55°﹣35°=20°.
故选:C.
9.解:形如y=kx+b(k≠0,b为常数)的函数称为一次函数,选项A没有k≠0,故不符合题意;
实数与数轴上的点具有一一对应的关系,故不存在在数轴上找不到对应的点.,故B错误,不符合题意;
∵+=3+4=7≠
∵x2≥0
∴x2+1>0
∴点P(﹣2,x2+1)的横坐标为负,纵坐标为正,故点P总在第二象限,故D正确.
故选:D.
10.解:由图象可得,
甲始终是匀速行进,乙的行进不是匀速的,刚开始一段时间匀速,后来提速,继续做匀速运动,故①正确;
甲用了5个小时到达目的地,故②正确;
乙比甲晚出发1小时,故③错误;
甲在出发4小时后被乙超过,故④错误;
由上可得,正确是①②,
故选:B.
二、填空题(共10小题,满分30分.)
11.解:∵等腰三角形底角相等,
∴180°﹣50°×2=80°,
∴顶角为80°.
故填80°.
12.解:由题意可知:m﹣3+m﹣7=0,
∴m=5,
∴m﹣3=2,
∴这个数为4,
故答案为:4
二、填空题(共9小题,满分60分.)
13.解:∵=2,2的平方根是±,
∴的平方根是±.
故答案为是±.
14.解:点P在第四象限内,点P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为(3,﹣4),
故答案为:(3,﹣4).
15.解:∵=4,
∴==40.
故答案为:40.
16.解:作点B关于x轴的对称点B′,连接AB′,交x轴于P,连接PB,此时PA+PB的值最小.
设直线AB′的解析式为y=kx+b,
把A(2,﹣4),B′(0,2)代入得到,
解得,
∴直线AB′的解析式为y=﹣3x+2,
令y=0,得到x=,
∴P(,0),
故答案为(,0).
17.解:由题意知正方形的边长为,
∵<<,
∴6<<7,
∴这两个整数是6和7,
故答案为:6和7.
18.解:设原来的边长为x,那么现在的体积为27x3,
则=3x,
所以它的棱长变为原来的3倍.
故答案为3.
解:由平移的性质可知,BC+AC=(300+300)cm,
∵∠ACB=90°,∠CAB=30°,
∴AC=BC,
∴BC+BC=300+300,
∴BC=300(cm),
故答案为300cm
20.解:以AB为底边构造等腰三角形ABC,
则点C在线段AB的垂直平分线上,
∴这样的等腰三角形可以构造4个.
故答案为:4.
21.解:CE=DE,理由如下:
连接CD,
在△ACD和△BDC中
,
∴△ACD≌△BDC(SSS),
∴∠ADC=∠BCD,
∴CE=DE.
22.解:连接BD,
∵AB=AD=6,∠A=60°,
∴△ABD是等边三角形,
∴∠ADB=60°,AB=AD=BD=6,
∵∠ADC=150°,
∴∠BDC=90°,
设CD=x,则BC=x+4,
在Rt△BCD中,可得x2+36=(x+4)2,
解得x=,
∴BC=+4=,
所以,四边形ABCD的周长为6+6++=21.
23.解:(1)设y1与x的函数关系式是y1=kx,
2k=2000,得k=1000,
即y1与x的函数关系式y1=1000x,
设y2与x的函数关系式是y2=ax+b,
,解得,
即y2与x的函数关系式是y2=500x+2000;
(2)令1000x=500x+2000,得x=4,
所以,销售量为4吨时,销售收入与销售成本相同;
(3)1000x﹣(500x+2000)=500x﹣2000.
把x=6代入上式,得500×6﹣2000=1000
所以,利润为1000元.
24.解:(1)如图,点P就是所要求作的点.
∵点C与点A关于x轴对称,
∴点C的坐标为(0,﹣4).
设直线BC的表达式为u=kx﹣4,
将点B的坐标(8,2)代入,得8k﹣4=2,
解:k=,
∴直线BC的解析式为y=x﹣4,
令x﹣4=0,解得x=
所以,点P的坐标为(,0).
(2)∵A,C关于x轴对称,
∴PA=PC,
∴PA+PB=PB+PC=BC,
∵B(8,2),C(0,﹣4),
∴PA+PB的最小值=BC==10.
25.证明:∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
在△ABF和△DCE中
∴△ABF≌△DCE(SAS),
∴∠GEF=∠GFE,
∴EG=FG.
26.解:△AOC是直角三角形;
理由:∵点C的横坐标为3,CB⊥OA,
∴OB=3,∠OBC=∠ABC=90°,
∴BC===,
∴AB===1,
∴OA=4,
∵OC2+AC2=12+4=16,OA2=16,
∴OC2+AC2=OA2,
∴∠ACO=90°,
∴△AOC是直角三角形.
27.解:(1)如图,四边形AB1C1D为所作,B,C两点的对应点B1、C1的坐标分别为(﹣2,﹣1),(﹣4,﹣5);
(2)四边形ABCD的面积=4×6﹣×2×1﹣×4×2﹣×4×2=15;
所以封闭图形ABCDC1B1的面积=2×15=30.
28.解:(1)由题意可得,
y=(100﹣40)(200﹣x)+(25﹣40)x=﹣75x+12000,
即纯收入y关于x的关系式是y=﹣75x+12000;
(2)令﹣75x+12000=0,
解得,x=160,
答:当x为160时,养殖场不赔不赚.
29.解:(1)点B(3,0)在直线l1上,
则3k+1=0,
解得,k=﹣,
∴直线l1的解析式为y=﹣x+1,
则点A的坐标为(0,1),
∵直线l2平行于y轴,点D的坐标为(1,0),
∴点C的横坐标为1,
当x=1时,y=﹣×1+1=,
∴点C的坐标为(1,);
(2)设点P的坐标为(1,b),
当点P在点C的上方,∠PAB=90°时,
PA=,AB==,PB=,
由勾股定理得,PB2=PA2+AB2,即4+b2=b2﹣2b+2+10,
解得,b=4,
则点P的坐标为(1,4);
当点P′在点C的下方,∠P′BA=90°时,
P′A=,AB==,P′B=,
由勾股定理得,P′A2=P′B2+AB2,即b2﹣2b+2=4+b2+10,
解得,b=﹣6,
则点P的坐标为(1,﹣6),
综上所述,当△ABP时以AB为直角边的直角三角形时,点P的坐标为(1,4)或(1,﹣6).
一、选择题(共10小题,满分30分.)
1.在π,,,0.303003,﹣中,无理数的个数是( )
A.1个 B.2个 C.3个 D.4个
2.下列在具体情境中不能确定平面内位置的是( )
A.东经37°,北纬21° B.电影院某放映厅7排3号
C.芝罘区南大街
D.烟台山灯塔北偏东60°方向,距离灯塔3千米
3.下列计算正确的是( )
A.=4 B.﹣= C.=±5 D.(﹣)2=4
4.利用全等三角形测量距离的依据是( )
A.全等三角形的对应角相等 B.全等三角形的对应边相等
C.大小和形状相同的两个三角形全等 D.三边对应相等的两个三角形全等
5.估计介于( )
A.0.4与0.5之间 B.0.5与0.6之间
C.0.6与0.7之间 D.0.7与0.8之间
6.将一副三角板按图中的方式叠放,则∠1的度数为( )
A.105° B.100° C.95° D.110°
7.直角坐标系中,若点P(a,b)在第二象限中,则点Q(﹣a,﹣b)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.如图,Rt△ABC中,∠ACB=90°,∠A=55°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( )
A.40° B.30° C.20° D.10°
9.下列说法正确的是( )
A.y=kx+b一定是一次函数
B.有的实数在数轴上找不到对应的点
C.长为,,的三条线段能组成直角三角形
D.无论x为何值,点P(﹣2,x2+1)总是在第二象限
10.A,B两地相距20km,甲乙两人沿同一条路线从A地到B地,如图的图象反映的是二人行进路程y(km)与行进时间t(h)之间的关系,有下列说法:①甲始终是匀速行进,乙的行进不是匀速的;②甲用了5个小时到达目的地;③乙比甲先出发1小时;④甲在出发4小时后被乙追上.在这些说法中,正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共10小题,满分30分.)
11.等腰三角形的一个底角为50°,则它的顶角的度数为 .
12.若一个数x的平方根是m﹣3和m﹣7,那么这个数x是 .
13.的平方根是 .
14.如果点P在第四象限内,点P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为 .
15.我们可以利用计算器求一个正数a的算术平方根,其操作方法是按顺序进行按键输入:.小明按键输入显示结果为4,则他按键输入显示结果应为 .
16.已知点A(2,﹣4),直线y=﹣x﹣2与y轴交于点B,在x轴上存在一点P,使得PA+PB的值最小,则点P的坐标为 .
17.一个正方形的面积为48平方单位,它的边长在两个相邻整数之间,这两个整数是 .
18.一个正方体的体积变为原来的27倍,则它的棱长变为原来的 倍.
19.如图所示,雪天路滑,为了让学生进教学楼更安全,校方特意在楼梯上铺了防滑地毯(图中虚线部分),小明同学测得∠A=30°,并且从老师那里得知地毯总长度为(300+300)厘米,那么这段楼梯的高度BC为 .
20.在如图的正方形网格中,每个小正方形的边长均为1,点A,B都在格点上,以AB为底边构造等腰三角形ABC,使点C也在格点上,如果腰长为无理数,则这样的等腰三角形可以构造 个.
解答题(共9小题,满分60分.)
21.如图,AD与BC交于点E,连接AC,BD,AD=BC,AC=BD.写出CE与DE相等的理由.
22.如图,在四边形ABCD中,AB=AD=6,∠A=60°,∠ADC=150°,BC﹣CD=4.求四边形ABCD的周长.
23.公司销售部门提供了某种产品销售收入(记为:y1/元)、销售成本(记为:y2/元)、销售量(记为:x/吨)方面的信息如下:
①x=0时,y2=2000;
②x=2时,y1=2000,y2=3000;
③y1与x成正比例函数关系;④y2与x成一次函数关系.1月亦团城8依据上述信息,解决下列问题:
(1)分别求出y1,y2与x的函数关系式;
(2)销售量为多少吨时,销售收入与销售成本相同?
(3)若销售量为6吨时,求公司的利润.(利润=销售收入﹣销售成本)
24.如图,点A的坐标为(0,4),点B的坐标为(8,2),点P是x轴上一点,且PA+PB的值最小,
(1)确定点P的位置,并求点P的坐标;
(2)求PA+PB的最小值.
25.如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:GE=GF.
26.在平面直角坐标系中,点A在x轴上,已知点C的横坐标为3,AC长为2,OC长为,CB⊥OA垂足为B.请你判断△AOC的形状,并说明理由.
27.如图是小亮同学设计的一个轴对称图形的一部分,其中点A,B,C,D都在直角坐标系网格的格点上,每个小正方形的边长都等于1.
(1)请画出关于y轴成轴对称图形的另一半,并写出B,C两点的对应点坐标.
(2)记B,C两点的对应点分别为B1,C1,请直接写出封闭图形ABCDC1B1的面积.
28.海水养殖是莱州经济产业的亮丽名片之一,某养殖场响应山东省加快新旧动能转换的号召,今年采用新技术投资养殖了200万笼扇贝,并且全部被订购,已知每笼扇贝的成本是40元,售价是100元,打捞出售过程中发现,一部分扇贝生长情况不合要求,最后只能按照25元一笼出售,如果纯收入为y万元,不合要求的扇贝有x万笼.
(1)求纯收入y关于x的关系式.
(2)当x为何值时,养殖场不赔不嫌?
29.如图,在平面直角坐标系中,直线l1:y=kx+1交y轴于点A,交x轴交于B(3,0),直线l2平行于y轴,交直线l1于点C,交x轴于点D,点D的坐标为(1,0)
(1)求直线l1的解析式和点A、C的坐标;
(2)点P是直线l2上一动点,连接PA、PB,当△ABP时以AB为直角边的直角三角形时,求点P的坐标.
参考答案:
一、选择题(共10小题,满分30分.)
1.解:,
∴在π,,,0.303003,﹣中,无理数有π,共2个.
故选:B.
2.解:A、东经37°,北纬21°物体的位置明确,故本选项错误;
B、电影院某放映厅7排3号物体的位置明确,故本选项错误;
C、芝罘区南大街无法确定物体的具体位置,故本选项正确;
D、烟台山灯塔北偏东60°方向,距离灯塔3千米物体的位置明确,故本选项错误;
故选:C.
3.解:A、=2,故此选项错误;
B、﹣,二次根式无意义,故此选项错误;
C、=5,故此选项错误;
D、(﹣)2=4,正确.
故选:D.
4.解:利用全等三角形测量距离的依据是全等三角形的对应边相等,
故选:B.
5.解:∵2.22=4.84,2.32=5.29,
∴2.2<<2.3,
∵=0.6,=0.65,
∴0.6<<0.65.
所以介于0.6与0.7之间.故选:C.
6.解:由图可知,∠2=90°﹣45°=45°,
∴∠1=180﹣45°﹣30°=105°.
故选:A.
7.解:∵点P(a,b)在第二象限中,
∴a<0,b>0,
∴﹣a>0,﹣b<0,
∴点Q(﹣a,﹣b)在第四象限,
故选:D.
8.解:在Rt△ABC中,∠ACB=90°,∠A=55°,
∴∠B=180°﹣90°﹣55°=35°,
由折叠可得:∠CA′D=∠A=55°,
又∵∠CA′D为△A′BD的外角,
∴∠CA′D=∠B+∠A′DB,
则∠A′DB=55°﹣35°=20°.
故选:C.
9.解:形如y=kx+b(k≠0,b为常数)的函数称为一次函数,选项A没有k≠0,故不符合题意;
实数与数轴上的点具有一一对应的关系,故不存在在数轴上找不到对应的点.,故B错误,不符合题意;
∵+=3+4=7≠
∵x2≥0
∴x2+1>0
∴点P(﹣2,x2+1)的横坐标为负,纵坐标为正,故点P总在第二象限,故D正确.
故选:D.
10.解:由图象可得,
甲始终是匀速行进,乙的行进不是匀速的,刚开始一段时间匀速,后来提速,继续做匀速运动,故①正确;
甲用了5个小时到达目的地,故②正确;
乙比甲晚出发1小时,故③错误;
甲在出发4小时后被乙超过,故④错误;
由上可得,正确是①②,
故选:B.
二、填空题(共10小题,满分30分.)
11.解:∵等腰三角形底角相等,
∴180°﹣50°×2=80°,
∴顶角为80°.
故填80°.
12.解:由题意可知:m﹣3+m﹣7=0,
∴m=5,
∴m﹣3=2,
∴这个数为4,
故答案为:4
二、填空题(共9小题,满分60分.)
13.解:∵=2,2的平方根是±,
∴的平方根是±.
故答案为是±.
14.解:点P在第四象限内,点P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为(3,﹣4),
故答案为:(3,﹣4).
15.解:∵=4,
∴==40.
故答案为:40.
16.解:作点B关于x轴的对称点B′,连接AB′,交x轴于P,连接PB,此时PA+PB的值最小.
设直线AB′的解析式为y=kx+b,
把A(2,﹣4),B′(0,2)代入得到,
解得,
∴直线AB′的解析式为y=﹣3x+2,
令y=0,得到x=,
∴P(,0),
故答案为(,0).
17.解:由题意知正方形的边长为,
∵<<,
∴6<<7,
∴这两个整数是6和7,
故答案为:6和7.
18.解:设原来的边长为x,那么现在的体积为27x3,
则=3x,
所以它的棱长变为原来的3倍.
故答案为3.
解:由平移的性质可知,BC+AC=(300+300)cm,
∵∠ACB=90°,∠CAB=30°,
∴AC=BC,
∴BC+BC=300+300,
∴BC=300(cm),
故答案为300cm
20.解:以AB为底边构造等腰三角形ABC,
则点C在线段AB的垂直平分线上,
∴这样的等腰三角形可以构造4个.
故答案为:4.
21.解:CE=DE,理由如下:
连接CD,
在△ACD和△BDC中
,
∴△ACD≌△BDC(SSS),
∴∠ADC=∠BCD,
∴CE=DE.
22.解:连接BD,
∵AB=AD=6,∠A=60°,
∴△ABD是等边三角形,
∴∠ADB=60°,AB=AD=BD=6,
∵∠ADC=150°,
∴∠BDC=90°,
设CD=x,则BC=x+4,
在Rt△BCD中,可得x2+36=(x+4)2,
解得x=,
∴BC=+4=,
所以,四边形ABCD的周长为6+6++=21.
23.解:(1)设y1与x的函数关系式是y1=kx,
2k=2000,得k=1000,
即y1与x的函数关系式y1=1000x,
设y2与x的函数关系式是y2=ax+b,
,解得,
即y2与x的函数关系式是y2=500x+2000;
(2)令1000x=500x+2000,得x=4,
所以,销售量为4吨时,销售收入与销售成本相同;
(3)1000x﹣(500x+2000)=500x﹣2000.
把x=6代入上式,得500×6﹣2000=1000
所以,利润为1000元.
24.解:(1)如图,点P就是所要求作的点.
∵点C与点A关于x轴对称,
∴点C的坐标为(0,﹣4).
设直线BC的表达式为u=kx﹣4,
将点B的坐标(8,2)代入,得8k﹣4=2,
解:k=,
∴直线BC的解析式为y=x﹣4,
令x﹣4=0,解得x=
所以,点P的坐标为(,0).
(2)∵A,C关于x轴对称,
∴PA=PC,
∴PA+PB=PB+PC=BC,
∵B(8,2),C(0,﹣4),
∴PA+PB的最小值=BC==10.
25.证明:∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
在△ABF和△DCE中
∴△ABF≌△DCE(SAS),
∴∠GEF=∠GFE,
∴EG=FG.
26.解:△AOC是直角三角形;
理由:∵点C的横坐标为3,CB⊥OA,
∴OB=3,∠OBC=∠ABC=90°,
∴BC===,
∴AB===1,
∴OA=4,
∵OC2+AC2=12+4=16,OA2=16,
∴OC2+AC2=OA2,
∴∠ACO=90°,
∴△AOC是直角三角形.
27.解:(1)如图,四边形AB1C1D为所作,B,C两点的对应点B1、C1的坐标分别为(﹣2,﹣1),(﹣4,﹣5);
(2)四边形ABCD的面积=4×6﹣×2×1﹣×4×2﹣×4×2=15;
所以封闭图形ABCDC1B1的面积=2×15=30.
28.解:(1)由题意可得,
y=(100﹣40)(200﹣x)+(25﹣40)x=﹣75x+12000,
即纯收入y关于x的关系式是y=﹣75x+12000;
(2)令﹣75x+12000=0,
解得,x=160,
答:当x为160时,养殖场不赔不赚.
29.解:(1)点B(3,0)在直线l1上,
则3k+1=0,
解得,k=﹣,
∴直线l1的解析式为y=﹣x+1,
则点A的坐标为(0,1),
∵直线l2平行于y轴,点D的坐标为(1,0),
∴点C的横坐标为1,
当x=1时,y=﹣×1+1=,
∴点C的坐标为(1,);
(2)设点P的坐标为(1,b),
当点P在点C的上方,∠PAB=90°时,
PA=,AB==,PB=,
由勾股定理得,PB2=PA2+AB2,即4+b2=b2﹣2b+2+10,
解得,b=4,
则点P的坐标为(1,4);
当点P′在点C的下方,∠P′BA=90°时,
P′A=,AB==,P′B=,
由勾股定理得,P′A2=P′B2+AB2,即b2﹣2b+2=4+b2+10,
解得,b=﹣6,
则点P的坐标为(1,﹣6),
综上所述,当△ABP时以AB为直角边的直角三角形时,点P的坐标为(1,4)或(1,﹣6).
同课章节目录
