2021-2022学年鲁教版(五四制)七年级数学第一学期期末综合复习题1(Word版 含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)七年级数学第一学期期末综合复习题1(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 262.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 08:36:12 | ||
图片预览


文档简介
2021-2022学年鲁教版七年级数学第一学期期末综合复习题1(附答案)
一、选择题(共12小题,满分36分.)
1.直线y=2x﹣3与y轴的交点坐标是( )
A.(0,2) B. C.(0,3) D.(0,﹣3)
2.的平方根是( )
A.2 B.﹣2 C. D.±2
3.若三角形的两边长分别为6cm,9cm,则其第三边的长可能为( )
A.2cm B.3cm C.7cm D.16cm
4.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠A=30°,AE=8cm,那么CE=( )
A.2cm B.3cm C.4cm D.5cm
5.直线y=2(x﹣1)向下平移3个单位长度得到的直线是( )
A.y=2(x﹣3) B.y=3x﹣3 C.y=2x﹣5 D.y=2x﹣2
6.一次函数y=kx+b满足kb>0,且y随x的增大而减小,则此函数的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.已知三角形三边长分别为2,9,x,若x为偶数,则这样的三角形个数为( )
A.1个 B.2个 C.3个 D.4个
8.如图,在Rt△ABC中,∠A=90°,BD是角平分线,DE垂直平分BC,AD=3,则AC的长为( )
A.9 B.5 C.4 D.3
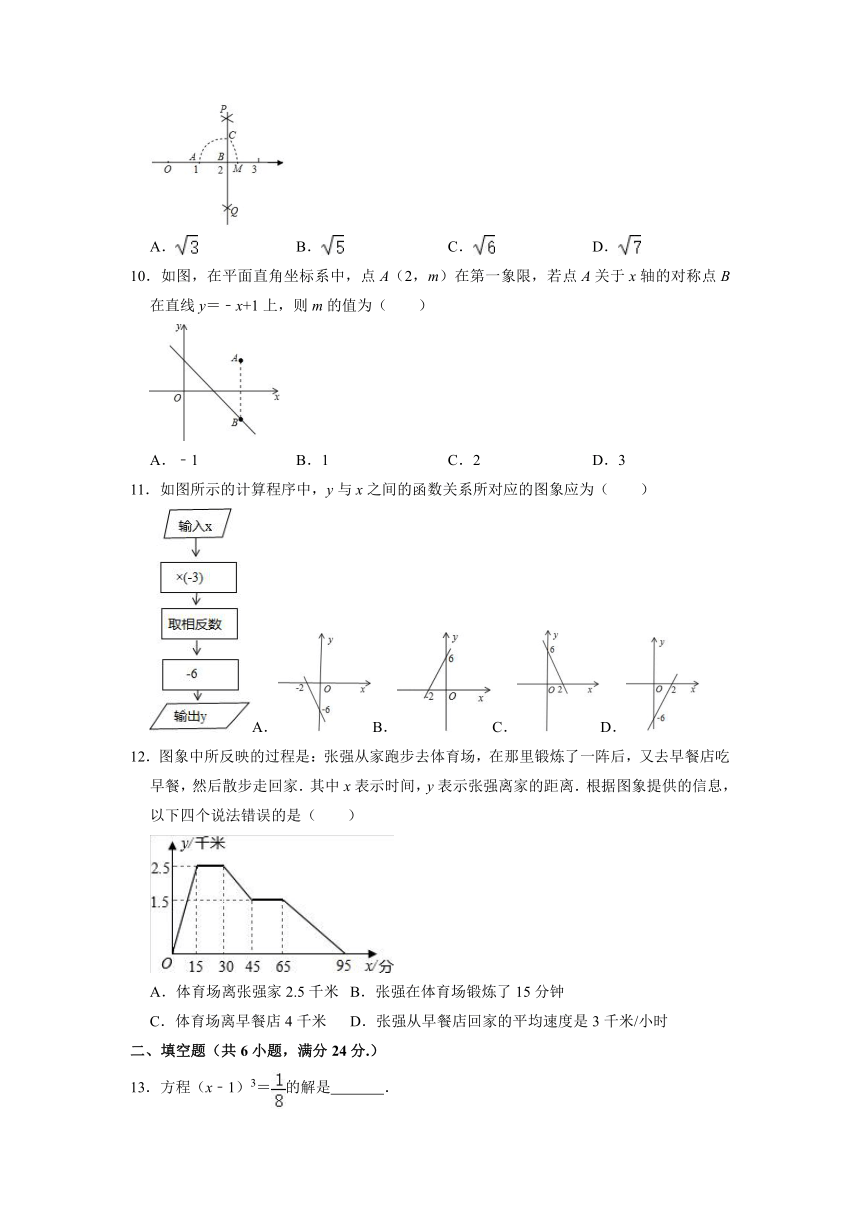
9.如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是( )
A. B. C. D.
10.如图,在平面直角坐标系中,点A(2,m)在第一象限,若点A关于x轴的对称点B在直线y=﹣x+1上,则m的值为( )
A.﹣1 B.1 C.2 D.3
11.如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
A.B.C.D.
12.图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )
A.体育场离张强家2.5千米 B.张强在体育场锻炼了15分钟
C.体育场离早餐店4千米 D.张强从早餐店回家的平均速度是3千米/小时
二、填空题(共6小题,满分24分.)
13.方程(x﹣1)3=的解是 .
14.如图,△ABC与△A′B′C′关于直线l对称,且∠A=102°,∠C′=25°,则∠B的度数为 .
15.已知点P的坐标为(5,﹣12),则点P到原点的距离为 .
16.某雷达探测目标得到的结果如图所示,若记图中目标A的位置为(3,30°),目标B的位置为(2,180°),目标C的位置为(4,240°),则图中目标D的位置可记为 .
17.如图,盒内长、宽、高分别是6cm、3cm、2cm,盒内可放木棒最长的长度是 .
18.已知y关于x的一次函数y=kx﹣8,其图象经过点(﹣5,2),当﹣2≤x≤2时,y的最大值是 .
三、解答题(共7小题,满分60分.))
19.已知点A(a+b,b﹣2)与B(5,﹣1)关于x轴对称,求:(a﹣b)2021的值.
20.如果一个正数a的两个平方根是x+2和3﹣2x.求(1)x和这个正数a的值;(2)22﹣3a的立方根.
21.计算:(﹣)2+﹣
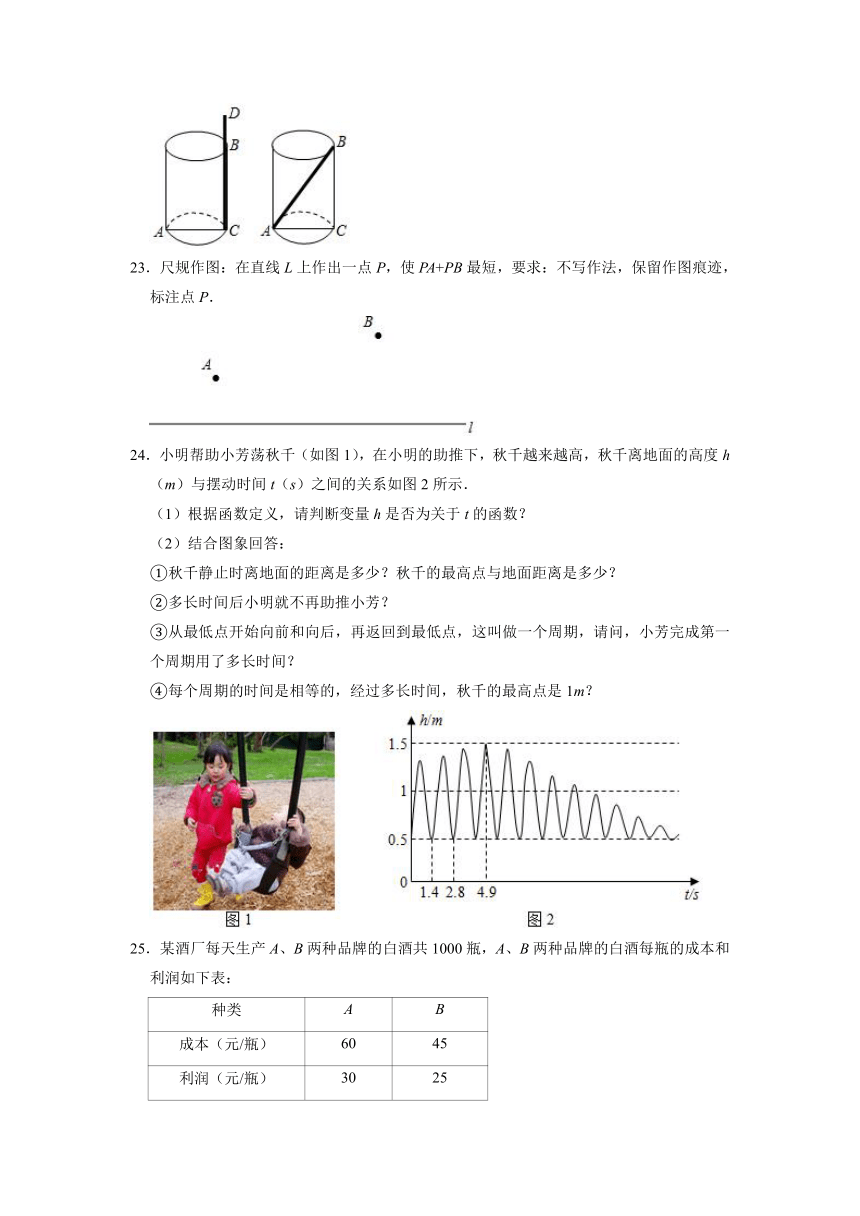
22.小芳在喝易拉罐饮料的时候,发现如果沿着罐内壁BC竖直放置吸管,露在外面部分BD=2厘米;如果尽最大长度往里放置,吸管正好和罐顶持平,已知易拉罐的底部是直径(AC)为8厘米的圆,请你求出吸管的长度.
23.尺规作图:在直线L上作出一点P,使PA+PB最短,要求:不写作法,保留作图痕迹,标注点P.
24.小明帮助小芳荡秋千(如图1),在小明的助推下,秋千越来越高,秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图2所示.
(1)根据函数定义,请判断变量h是否为关于t的函数?
(2)结合图象回答:
①秋千静止时离地面的距离是多少?秋千的最高点与地面距离是多少?
②多长时间后小明就不再助推小芳?
③从最低点开始向前和向后,再返回到最低点,这叫做一个周期,请问,小芳完成第一个周期用了多长时间?
④每个周期的时间是相等的,经过多长时间,秋千的最高点是1m?
25.某酒厂每天生产A、B两种品牌的白酒共1000瓶,A、B两种品牌的白酒每瓶的成本和利润如下表:
种类 A B
成本(元/瓶) 60 45
利润(元/瓶) 30 25
设每天生产A种品牌白酒x瓶,这两种酒每天共获利润y元,
(1)写出y关于x的函数表达式;
(2)如果该酒厂每天对这两种酒投入成本51000元,那么这两种酒每天获利多少元?
参考答案:
一、选择题(本大题共12小题,每小题3分,共36分.)
1.解:把x=0代入y=2x﹣3得y=﹣3,
所以直线y=2x﹣3与y轴的交点坐标是(0,﹣3).
故选:D.
2解:=2,2的平方根是±,
故选:C.
3.解:设第三边长为xcm.
由三角形三边关系定理得9﹣6<x<9+6,
解得3<x<15.故选:C.
4.解:∵BE平分∠ABC,ED⊥AB,EC⊥AC,
∴ED=EC,
在Rt△ADE中,∵∠A=30°,
∴ED=AE=×8=4,
∴CE=4cm.故选:C.
5.解:将线y=2(x﹣1)向下平移3个单位长度后得到的直线解析式为y=2(x﹣1)﹣3,
即y=2x﹣5.
故选:C.
6.解:根据y随x的增大而减小得:k<0,又kb>0,则b<0,
故此函数的图象经过第二、三、四象限,
即不经过第一象限.
故选:A.
7.解:由题意可得,
9﹣2<x<9+2,
解得,7<x<11,
∵x为偶数,
∴x=8、10,即这样的三角形有2个.
故选:B.
8.解:∵BD是角平分线,DE⊥BC,∠A=90°,
∴DE=AD=3,
在Rt△ADB和Rt△EDB中,
∵,
∴Rt△ADB≌Rt△EDB(HL),
∴BE=AB,
∵DE是BC的垂直平分线,
∴CE=BE,
∴BC=2AB,
∴∠C=30°,
∴CD=2DE=6,
∴AC=CD+AD=6+3=9,
故选:A.
9.解:如图所示:连接OC,
由题意可得:OB=2,BC=1,
则OC==,
故点M对应的数是:.
故选:B.
10.解:∵点A(2,m),
∴点A关于x轴的对称点B(2,﹣m),
∵B在直线y=﹣x+1上,
∴﹣m=﹣2+1=﹣1,
m=1,
故选:B.
11.解:根据程序框图可得y=﹣x×(﹣3)﹣6=3x﹣6,化简,得y=3x﹣6,
y=3x﹣6的图象与y轴的交点为(0,﹣6),与x轴的交点为(2,0).
故选:D.
12.解:A、由函数图象可知,体育场离张强家2.5千米,故A选项正确;
B、由图象可得出张强在体育场锻炼30﹣15=15(分钟),故B选项正确;
C、体育场离张强家2.5千米,体育场离早餐店距离无法确定,因为题目没说体育馆,早餐店和家三者在同一直线上,故C选项错误;
D、∵张强从早餐店回家所用时间为95﹣65=30(分钟),距离为1.5km,
∴张强从早餐店回家的平均速度1.5÷0.5=3(千米/时),故D选项正确.
故选:C.
二、填空题(共6小题,满分24分.)
13.解:因为(x﹣1)3=,
所以x﹣1=,
所以x=,
故答案为:x=.
14.解:∵△ABC与△A′B′C′关于直线l对称,且∠A=102°,∠C′=25°,
∴∠C=25°,
∴∠B=180°﹣∠A﹣∠C=53°.
故答案为:53°.
15.解:∵点P的坐标为(5,﹣12),
∴点P到原点的距离OP==13,
故答案为:13.
16.解:由图可知,图中目标D的位置可记为(5,120°).
故答案为:(5,120°).
17.解:本题需先求出长和宽组成的长方形的对角线长为=3 cm.
这根最长的棍子和矩形的高,以及长和宽组成的长方形的对角线组成了直角三角形.
盒内可放木棒最长的长度是 =7cm.
故答案为:7.
18.解:将(﹣5,2)代入y=kx﹣8,得:2=﹣5k﹣8,
解得:k=﹣2,
∴一次函数的解析式为y=﹣2x﹣8.
∵k=﹣2<0,
∴y值随x值的增大而减小,
∴当x=﹣2时,y取得最大值,最大值为﹣4.
故答案为:﹣4.
三、解答题(共7小题,满分60分.)
19.解:∵点A(a+b,b﹣2)与B(5,﹣1)关于x轴对称,
∴a+b=5,b﹣2=1,
解得:a=2,b=3,
∴(a﹣b)2021=(2﹣3)2021=﹣1.
20.解:(1)根据题意,x+2+3﹣2x=0,
解得x=5,
即a=49
(2)由(1)得a=49,
故22﹣3a=22﹣3×49=﹣125
故=﹣5;
21.解:(﹣)2+﹣
=0.4﹣0.2﹣1.4
=﹣1.2.
22.解:根据勾股定理得,AB2=BC2+AC2,
∴AB2=(AB﹣2)2+82,
解得:AB=17,
答:吸管的长度17cm.
23.解:如图,点P为所作.
24.解:(1)h是t的函数是两个变量、每一个时间t的确定值,高度 h都有唯一的值与其对应,
故变量h是关于t的函数;
(2)由图象知,①秋千静止时离地面的距离是0.5米,秋千的最高点与地面距离是1.5米;
②4.9秒后小明就不再助推小芳;
③小芳完成第一个周期用了2.8秒;
④∵每个周期的时间是相等的,
观察图象可知:
经过4个周期时,第5个周期刚刚开始向前时,秋千的最高点是1m,
所以4×2.8+2.8÷4=11.9
所以经过11.9秒,秋千的最高点是1m.
25.解:(1)由题意可得,
y=30x+25(1000﹣x)=5x+25000,
即y关于x的函数表达式是y=5x+25000;
(2)由题意可得,
60x+45(1000﹣x)=51000,
解得,x=400,
∴1000﹣x=600,
∴这两种酒每天获利:5×400+25000=27000(元),
答:这两种酒每天获利27000元
一、选择题(共12小题,满分36分.)
1.直线y=2x﹣3与y轴的交点坐标是( )
A.(0,2) B. C.(0,3) D.(0,﹣3)
2.的平方根是( )
A.2 B.﹣2 C. D.±2
3.若三角形的两边长分别为6cm,9cm,则其第三边的长可能为( )
A.2cm B.3cm C.7cm D.16cm
4.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠A=30°,AE=8cm,那么CE=( )
A.2cm B.3cm C.4cm D.5cm
5.直线y=2(x﹣1)向下平移3个单位长度得到的直线是( )
A.y=2(x﹣3) B.y=3x﹣3 C.y=2x﹣5 D.y=2x﹣2
6.一次函数y=kx+b满足kb>0,且y随x的增大而减小,则此函数的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.已知三角形三边长分别为2,9,x,若x为偶数,则这样的三角形个数为( )
A.1个 B.2个 C.3个 D.4个
8.如图,在Rt△ABC中,∠A=90°,BD是角平分线,DE垂直平分BC,AD=3,则AC的长为( )
A.9 B.5 C.4 D.3
9.如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是( )
A. B. C. D.
10.如图,在平面直角坐标系中,点A(2,m)在第一象限,若点A关于x轴的对称点B在直线y=﹣x+1上,则m的值为( )
A.﹣1 B.1 C.2 D.3
11.如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
A.B.C.D.
12.图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )
A.体育场离张强家2.5千米 B.张强在体育场锻炼了15分钟
C.体育场离早餐店4千米 D.张强从早餐店回家的平均速度是3千米/小时
二、填空题(共6小题,满分24分.)
13.方程(x﹣1)3=的解是 .
14.如图,△ABC与△A′B′C′关于直线l对称,且∠A=102°,∠C′=25°,则∠B的度数为 .
15.已知点P的坐标为(5,﹣12),则点P到原点的距离为 .
16.某雷达探测目标得到的结果如图所示,若记图中目标A的位置为(3,30°),目标B的位置为(2,180°),目标C的位置为(4,240°),则图中目标D的位置可记为 .
17.如图,盒内长、宽、高分别是6cm、3cm、2cm,盒内可放木棒最长的长度是 .
18.已知y关于x的一次函数y=kx﹣8,其图象经过点(﹣5,2),当﹣2≤x≤2时,y的最大值是 .
三、解答题(共7小题,满分60分.))
19.已知点A(a+b,b﹣2)与B(5,﹣1)关于x轴对称,求:(a﹣b)2021的值.
20.如果一个正数a的两个平方根是x+2和3﹣2x.求(1)x和这个正数a的值;(2)22﹣3a的立方根.
21.计算:(﹣)2+﹣
22.小芳在喝易拉罐饮料的时候,发现如果沿着罐内壁BC竖直放置吸管,露在外面部分BD=2厘米;如果尽最大长度往里放置,吸管正好和罐顶持平,已知易拉罐的底部是直径(AC)为8厘米的圆,请你求出吸管的长度.
23.尺规作图:在直线L上作出一点P,使PA+PB最短,要求:不写作法,保留作图痕迹,标注点P.
24.小明帮助小芳荡秋千(如图1),在小明的助推下,秋千越来越高,秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图2所示.
(1)根据函数定义,请判断变量h是否为关于t的函数?
(2)结合图象回答:
①秋千静止时离地面的距离是多少?秋千的最高点与地面距离是多少?
②多长时间后小明就不再助推小芳?
③从最低点开始向前和向后,再返回到最低点,这叫做一个周期,请问,小芳完成第一个周期用了多长时间?
④每个周期的时间是相等的,经过多长时间,秋千的最高点是1m?
25.某酒厂每天生产A、B两种品牌的白酒共1000瓶,A、B两种品牌的白酒每瓶的成本和利润如下表:
种类 A B
成本(元/瓶) 60 45
利润(元/瓶) 30 25
设每天生产A种品牌白酒x瓶,这两种酒每天共获利润y元,
(1)写出y关于x的函数表达式;
(2)如果该酒厂每天对这两种酒投入成本51000元,那么这两种酒每天获利多少元?
参考答案:
一、选择题(本大题共12小题,每小题3分,共36分.)
1.解:把x=0代入y=2x﹣3得y=﹣3,
所以直线y=2x﹣3与y轴的交点坐标是(0,﹣3).
故选:D.
2解:=2,2的平方根是±,
故选:C.
3.解:设第三边长为xcm.
由三角形三边关系定理得9﹣6<x<9+6,
解得3<x<15.故选:C.
4.解:∵BE平分∠ABC,ED⊥AB,EC⊥AC,
∴ED=EC,
在Rt△ADE中,∵∠A=30°,
∴ED=AE=×8=4,
∴CE=4cm.故选:C.
5.解:将线y=2(x﹣1)向下平移3个单位长度后得到的直线解析式为y=2(x﹣1)﹣3,
即y=2x﹣5.
故选:C.
6.解:根据y随x的增大而减小得:k<0,又kb>0,则b<0,
故此函数的图象经过第二、三、四象限,
即不经过第一象限.
故选:A.
7.解:由题意可得,
9﹣2<x<9+2,
解得,7<x<11,
∵x为偶数,
∴x=8、10,即这样的三角形有2个.
故选:B.
8.解:∵BD是角平分线,DE⊥BC,∠A=90°,
∴DE=AD=3,
在Rt△ADB和Rt△EDB中,
∵,
∴Rt△ADB≌Rt△EDB(HL),
∴BE=AB,
∵DE是BC的垂直平分线,
∴CE=BE,
∴BC=2AB,
∴∠C=30°,
∴CD=2DE=6,
∴AC=CD+AD=6+3=9,
故选:A.
9.解:如图所示:连接OC,
由题意可得:OB=2,BC=1,
则OC==,
故点M对应的数是:.
故选:B.
10.解:∵点A(2,m),
∴点A关于x轴的对称点B(2,﹣m),
∵B在直线y=﹣x+1上,
∴﹣m=﹣2+1=﹣1,
m=1,
故选:B.
11.解:根据程序框图可得y=﹣x×(﹣3)﹣6=3x﹣6,化简,得y=3x﹣6,
y=3x﹣6的图象与y轴的交点为(0,﹣6),与x轴的交点为(2,0).
故选:D.
12.解:A、由函数图象可知,体育场离张强家2.5千米,故A选项正确;
B、由图象可得出张强在体育场锻炼30﹣15=15(分钟),故B选项正确;
C、体育场离张强家2.5千米,体育场离早餐店距离无法确定,因为题目没说体育馆,早餐店和家三者在同一直线上,故C选项错误;
D、∵张强从早餐店回家所用时间为95﹣65=30(分钟),距离为1.5km,
∴张强从早餐店回家的平均速度1.5÷0.5=3(千米/时),故D选项正确.
故选:C.
二、填空题(共6小题,满分24分.)
13.解:因为(x﹣1)3=,
所以x﹣1=,
所以x=,
故答案为:x=.
14.解:∵△ABC与△A′B′C′关于直线l对称,且∠A=102°,∠C′=25°,
∴∠C=25°,
∴∠B=180°﹣∠A﹣∠C=53°.
故答案为:53°.
15.解:∵点P的坐标为(5,﹣12),
∴点P到原点的距离OP==13,
故答案为:13.
16.解:由图可知,图中目标D的位置可记为(5,120°).
故答案为:(5,120°).
17.解:本题需先求出长和宽组成的长方形的对角线长为=3 cm.
这根最长的棍子和矩形的高,以及长和宽组成的长方形的对角线组成了直角三角形.
盒内可放木棒最长的长度是 =7cm.
故答案为:7.
18.解:将(﹣5,2)代入y=kx﹣8,得:2=﹣5k﹣8,
解得:k=﹣2,
∴一次函数的解析式为y=﹣2x﹣8.
∵k=﹣2<0,
∴y值随x值的增大而减小,
∴当x=﹣2时,y取得最大值,最大值为﹣4.
故答案为:﹣4.
三、解答题(共7小题,满分60分.)
19.解:∵点A(a+b,b﹣2)与B(5,﹣1)关于x轴对称,
∴a+b=5,b﹣2=1,
解得:a=2,b=3,
∴(a﹣b)2021=(2﹣3)2021=﹣1.
20.解:(1)根据题意,x+2+3﹣2x=0,
解得x=5,
即a=49
(2)由(1)得a=49,
故22﹣3a=22﹣3×49=﹣125
故=﹣5;
21.解:(﹣)2+﹣
=0.4﹣0.2﹣1.4
=﹣1.2.
22.解:根据勾股定理得,AB2=BC2+AC2,
∴AB2=(AB﹣2)2+82,
解得:AB=17,
答:吸管的长度17cm.
23.解:如图,点P为所作.
24.解:(1)h是t的函数是两个变量、每一个时间t的确定值,高度 h都有唯一的值与其对应,
故变量h是关于t的函数;
(2)由图象知,①秋千静止时离地面的距离是0.5米,秋千的最高点与地面距离是1.5米;
②4.9秒后小明就不再助推小芳;
③小芳完成第一个周期用了2.8秒;
④∵每个周期的时间是相等的,
观察图象可知:
经过4个周期时,第5个周期刚刚开始向前时,秋千的最高点是1m,
所以4×2.8+2.8÷4=11.9
所以经过11.9秒,秋千的最高点是1m.
25.解:(1)由题意可得,
y=30x+25(1000﹣x)=5x+25000,
即y关于x的函数表达式是y=5x+25000;
(2)由题意可得,
60x+45(1000﹣x)=51000,
解得,x=400,
∴1000﹣x=600,
∴这两种酒每天获利:5×400+25000=27000(元),
答:这两种酒每天获利27000元
同课章节目录
