人教版数学七年级上册2.2.3整式的加减课件(共28张PPT)
文档属性
| 名称 | 人教版数学七年级上册2.2.3整式的加减课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 813.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-19 14:10:16 | ||
图片预览








文档简介
(共28张PPT)
2.2 整式的加减
(第3课时)
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段。列车在冻土地段的行驶速度是100千米/时,在非冻土地段的行驶速度可以达到120千米/时,请根据这些数据回答下列问题:
(3)在格尔木到拉萨路段,列车通过冻土地段比通过非冻土地段多用0.5h,如果通过冻土地段需要u h,则这段铁路的全长可以怎样表示 冻土地段与非冻土地段相差多少千米
思考 问题
全长 100u+120(u-0.5)
书本53页
相差 100u-120(u-0.5)
= 100u+120u-60
= 220u-60
= 100u-120u+60
= -20u+60
全长 100u+120(u-0.5)
相差 100u-120(u-0.5)
= 100u+120u-60
= 100u-120u+60
+120(u-0.5)
= 120u-60
-120(u-0.5)
= -120u+60
去括号时,括号内的各项的符号的变化的规律是什么
问题
☆找出多项式8a+2b+(5a-b)中的同类项,想一想怎样才能合并同类项。
分析:8a与5a是同类项,2b与-b是同类项。由于5a和-b在括号内,要先去括号,才能合并同类项。
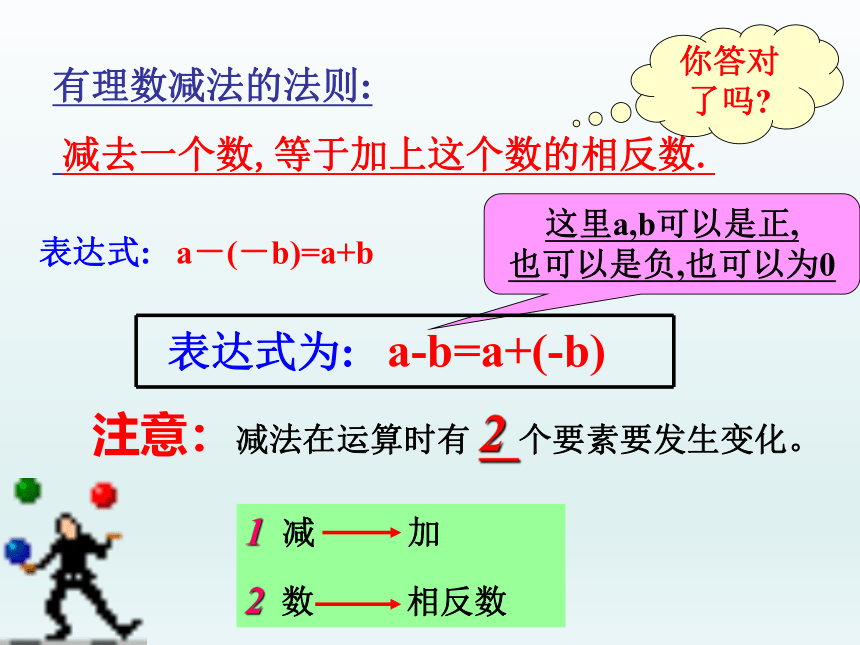
有理数减法的法则:
减去一个数,等于加上这个数的相反数.
表达式为: a-b=a+(-b)
这里a,b可以是正,
也可以是负,也可以为0
你答对了吗
注意:减法在运算时有 2 个要素要发生变化。
1 减 加
2 数 相反数
表达式: a-(-b)=a+b
我们容易得到:
① :13+(7-5)= 13+7-5
② :9a+(6a-a)=9a + 6a-a
③ :13-(7-5)= 13-7+5
④ : 9a-(6a-a)=9a - 6a+a
减法法则: a-(-b)=a+b
减法法则: a-b=a+(-b)
由上面的①、②式:
① :13+(7-5)= 13+7-5
② :9a+(6a-a)=9a + 6a-a
我们得到:括号前是“+”号,把括号和它前面和“+”号去掉,括号里各项都不变符号。
由上面的③、④式:
③ : 13-(7-5)= 13-7+5
④ : 9a-(6a-a)=9a - 6a+a
我们得到:括号前是“-”号,把括号和它前面和“-”号去掉,括号里各项都
改变符号。
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同.
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反
去括号法则:
正同负反
正不变负变
例1 去括号:
(1)a+(-b+c-d);
(2)a-(-b+c-d).
解: (1)a+(-b+c-d)
= a-b +c-d
(2) a-(-b+c-d)
= a+b-c+d
例2 先去括号,再合并同类项:
(1)8a+2b+(5a-b);
(2)6a+2(a-c).
解: (1)8a+2b+(5a-b)
= 8a+2b+ 5a-b ——不用变号
=13a+b ——合并同类项
(2)6a+2(a-c)
= 6a+(2a-2c) ——乘法分配律
=6a+2a-2c ——不用变号
= 8a-2c ——合并同类项
例3 先去括号,再合并同类项:
(1)8a+2b-(5a-b);
(2)6a-2(a-c).
解: (1)8a+2b-(5a-b)
= 8a+2b- 5a+b ——变号
=3a+b ——合并同类项
(2)6a-2(a-c)
= 6a-(2a-2c) ——乘法分配律
=6a-2a+2c ——变号
= 4a+2c ——合并同类项
例4 化简(5a-3b) +3(a2-2b)
解: (5a-3b) +3(a2-2b)
= 5a-3b+(3 a2 -6b)——乘法分配律
= 5a-3b+ 3 a2 -6b ——括号前是正,不变号
= 3 a2 + 5a-9b—— 同类项记得要合并
例5 化简(5a-3b) -3(a2-2b)
解: (5a-3b) -3(a2-2b)
= 5a-3b-(3 a2 -6b)——乘法分配律
= 5a-3b- 3 a2 +6b ——括号前是负,要变号
= - 3 a2 +5a+3b—— 同类项记得要合并
2x-3y
5x+4y
(
)
(
)
+
(1)
例6 计算
解:(2x-3y)+(5x+4y)
=2x-3y+5x+4y
=2x+5x-3y+4y
=7x+y
去括号
}
找出同类项
合并同类项
例6 计算
解:(5x+4y)-(2x-3y)
= 5x+4y -2x+3y
=5x-2x+4y+3y
=3x+7y
尝试练习:(8a-7b)-(4a-5b)
整式的加减运算通常是先( ),
再( )。
去括号
合并同类项
(2)( 5x+4y)-(2x-3y)
8a-7b
4a-5b
(
)
(
)
-
(1)
例7 计算
解:原式=
去括号
找出同类项
合并同类项
8a-7b-4a+5b
=4a-2b
8a-7b
4a-5b
(
)
(
)
+
(2)
例7 计算
解:原式=
去括号
找出同类项
合并同类项
8a-7b+4a-5b
=12a-12b
课本P67练习 1, 2
成长的足迹
例5 两船从同一港口同时出发反向而行,甲船顺水,
乙船逆水,两船在静水中的速度都是50 km/h, 水流
速度是a km/h .
2 h 后两船相距多远
(2) 2 h 后甲船比乙船多航行多少千米
解:顺水速度=船速+水速= (50+a) km/h
逆水速度=船速-水速=(50-a) km/h .
2 h 后两船相距 (单位:km)
(2) 2 h 后甲船比乙船多航行(单位:km)
= (100+2a)+(100-2a)
2(50+a)+2(50-a)
= 200
= (100+2a)-(100-2a)
2(50+a)-2(50-a)
= 4a
= 100+2a-100+2a
例4 用式子表示十位上的数是a,个位上的数是b
的两位数,再把这个两位数的十位上的数与个位
上的数交换位置,计算所得数与原数的和,所得
数与原数的和能被11整除吗?
例4 用式子表示十位上的数是a,个位上的数是b
的两位数,再把这个两位数的十位上的数与个位
上的数交换位置,计算所得数与原数的和,所得
数与原数的和能被11整除吗?
解:原来的两位数为10a+b,
新的两位数为10b+a
两个数的和为10a+b+10b+a
∴所得数与原数的和能被11整除.
例5 已知m是绝对值最小的有理数,且
与 是同类项,
求 : 的值
例5 已知m是绝对值最小的有理数,且 与
是同类项,求
的值.
解:∵m是绝对值最小的有理数,∴m=0
∵ 与 是同类项
∴ ∴
∴
例6 若 ,
求: 的值.
例6 若 ,
求: 的值.
解: ①
②
①+②得:
课堂小结:
1.化简求值
2.把实际问题抽象为数学模型
3.挖掘已知条件,构造所求整式
2.2 整式的加减
(第3课时)
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段。列车在冻土地段的行驶速度是100千米/时,在非冻土地段的行驶速度可以达到120千米/时,请根据这些数据回答下列问题:
(3)在格尔木到拉萨路段,列车通过冻土地段比通过非冻土地段多用0.5h,如果通过冻土地段需要u h,则这段铁路的全长可以怎样表示 冻土地段与非冻土地段相差多少千米
思考 问题
全长 100u+120(u-0.5)
书本53页
相差 100u-120(u-0.5)
= 100u+120u-60
= 220u-60
= 100u-120u+60
= -20u+60
全长 100u+120(u-0.5)
相差 100u-120(u-0.5)
= 100u+120u-60
= 100u-120u+60
+120(u-0.5)
= 120u-60
-120(u-0.5)
= -120u+60
去括号时,括号内的各项的符号的变化的规律是什么
问题
☆找出多项式8a+2b+(5a-b)中的同类项,想一想怎样才能合并同类项。
分析:8a与5a是同类项,2b与-b是同类项。由于5a和-b在括号内,要先去括号,才能合并同类项。
有理数减法的法则:
减去一个数,等于加上这个数的相反数.
表达式为: a-b=a+(-b)
这里a,b可以是正,
也可以是负,也可以为0
你答对了吗
注意:减法在运算时有 2 个要素要发生变化。
1 减 加
2 数 相反数
表达式: a-(-b)=a+b
我们容易得到:
① :13+(7-5)= 13+7-5
② :9a+(6a-a)=9a + 6a-a
③ :13-(7-5)= 13-7+5
④ : 9a-(6a-a)=9a - 6a+a
减法法则: a-(-b)=a+b
减法法则: a-b=a+(-b)
由上面的①、②式:
① :13+(7-5)= 13+7-5
② :9a+(6a-a)=9a + 6a-a
我们得到:括号前是“+”号,把括号和它前面和“+”号去掉,括号里各项都不变符号。
由上面的③、④式:
③ : 13-(7-5)= 13-7+5
④ : 9a-(6a-a)=9a - 6a+a
我们得到:括号前是“-”号,把括号和它前面和“-”号去掉,括号里各项都
改变符号。
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同.
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反
去括号法则:
正同负反
正不变负变
例1 去括号:
(1)a+(-b+c-d);
(2)a-(-b+c-d).
解: (1)a+(-b+c-d)
= a-b +c-d
(2) a-(-b+c-d)
= a+b-c+d
例2 先去括号,再合并同类项:
(1)8a+2b+(5a-b);
(2)6a+2(a-c).
解: (1)8a+2b+(5a-b)
= 8a+2b+ 5a-b ——不用变号
=13a+b ——合并同类项
(2)6a+2(a-c)
= 6a+(2a-2c) ——乘法分配律
=6a+2a-2c ——不用变号
= 8a-2c ——合并同类项
例3 先去括号,再合并同类项:
(1)8a+2b-(5a-b);
(2)6a-2(a-c).
解: (1)8a+2b-(5a-b)
= 8a+2b- 5a+b ——变号
=3a+b ——合并同类项
(2)6a-2(a-c)
= 6a-(2a-2c) ——乘法分配律
=6a-2a+2c ——变号
= 4a+2c ——合并同类项
例4 化简(5a-3b) +3(a2-2b)
解: (5a-3b) +3(a2-2b)
= 5a-3b+(3 a2 -6b)——乘法分配律
= 5a-3b+ 3 a2 -6b ——括号前是正,不变号
= 3 a2 + 5a-9b—— 同类项记得要合并
例5 化简(5a-3b) -3(a2-2b)
解: (5a-3b) -3(a2-2b)
= 5a-3b-(3 a2 -6b)——乘法分配律
= 5a-3b- 3 a2 +6b ——括号前是负,要变号
= - 3 a2 +5a+3b—— 同类项记得要合并
2x-3y
5x+4y
(
)
(
)
+
(1)
例6 计算
解:(2x-3y)+(5x+4y)
=2x-3y+5x+4y
=2x+5x-3y+4y
=7x+y
去括号
}
找出同类项
合并同类项
例6 计算
解:(5x+4y)-(2x-3y)
= 5x+4y -2x+3y
=5x-2x+4y+3y
=3x+7y
尝试练习:(8a-7b)-(4a-5b)
整式的加减运算通常是先( ),
再( )。
去括号
合并同类项
(2)( 5x+4y)-(2x-3y)
8a-7b
4a-5b
(
)
(
)
-
(1)
例7 计算
解:原式=
去括号
找出同类项
合并同类项
8a-7b-4a+5b
=4a-2b
8a-7b
4a-5b
(
)
(
)
+
(2)
例7 计算
解:原式=
去括号
找出同类项
合并同类项
8a-7b+4a-5b
=12a-12b
课本P67练习 1, 2
成长的足迹
例5 两船从同一港口同时出发反向而行,甲船顺水,
乙船逆水,两船在静水中的速度都是50 km/h, 水流
速度是a km/h .
2 h 后两船相距多远
(2) 2 h 后甲船比乙船多航行多少千米
解:顺水速度=船速+水速= (50+a) km/h
逆水速度=船速-水速=(50-a) km/h .
2 h 后两船相距 (单位:km)
(2) 2 h 后甲船比乙船多航行(单位:km)
= (100+2a)+(100-2a)
2(50+a)+2(50-a)
= 200
= (100+2a)-(100-2a)
2(50+a)-2(50-a)
= 4a
= 100+2a-100+2a
例4 用式子表示十位上的数是a,个位上的数是b
的两位数,再把这个两位数的十位上的数与个位
上的数交换位置,计算所得数与原数的和,所得
数与原数的和能被11整除吗?
例4 用式子表示十位上的数是a,个位上的数是b
的两位数,再把这个两位数的十位上的数与个位
上的数交换位置,计算所得数与原数的和,所得
数与原数的和能被11整除吗?
解:原来的两位数为10a+b,
新的两位数为10b+a
两个数的和为10a+b+10b+a
∴所得数与原数的和能被11整除.
例5 已知m是绝对值最小的有理数,且
与 是同类项,
求 : 的值
例5 已知m是绝对值最小的有理数,且 与
是同类项,求
的值.
解:∵m是绝对值最小的有理数,∴m=0
∵ 与 是同类项
∴ ∴
∴
例6 若 ,
求: 的值.
例6 若 ,
求: 的值.
解: ①
②
①+②得:
课堂小结:
1.化简求值
2.把实际问题抽象为数学模型
3.挖掘已知条件,构造所求整式
