第二章 机械振动 期末综合复习优选测评卷(Word版含答案)
文档属性
| 名称 | 第二章 机械振动 期末综合复习优选测评卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 374.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-18 22:21:44 | ||
图片预览



文档简介
第二章 机械振动 期末综合复习优选测评卷
一、单选题
1.一单摆由甲地移到乙地后,发现走时变快了,其变快的原因及调整的方法是( )
A.g甲>g乙,将摆长缩短
B.g甲C.g甲D.g甲>g乙,将摆长放长
2.如图为某质点沿x轴做简谐运动的图象,下列说法中正确的是( )
A.在t=4s时质点速度最大,加速度为0
B.在t=1s时,质点速度和加速度都达到最大值
C.在0到1s时间内,质点速度和加速度方向相同
D.在t=2s时,质点的位移沿x轴负方向,加速度也沿x轴负方向
3.某弹簧振子沿x轴的简谐运动图象如图所示,下列描述正确的是( )
A.t =1 s时,振子的速度为零,加速度为负的最大值
B.t =2 s时,振子的速度为负,加速度为正的最大值
C.t =3 s时,振子的速度为负的最大值,加速度为零
D.t =4 s时,振子的速度为正,加速度为负的最大值
4.弹簧振子做简谐振动,0为平衡位置,以它从0点开始运动作为计时起点,经过0.3s后第一次到达M点,再经过0.2s后第二次达达M点,则它第三次到达M点还需要经过的时间为:
①1.1s ②1.4s ③1.6s ④1/3s
A.①② B.③④ C.①③ D.②④
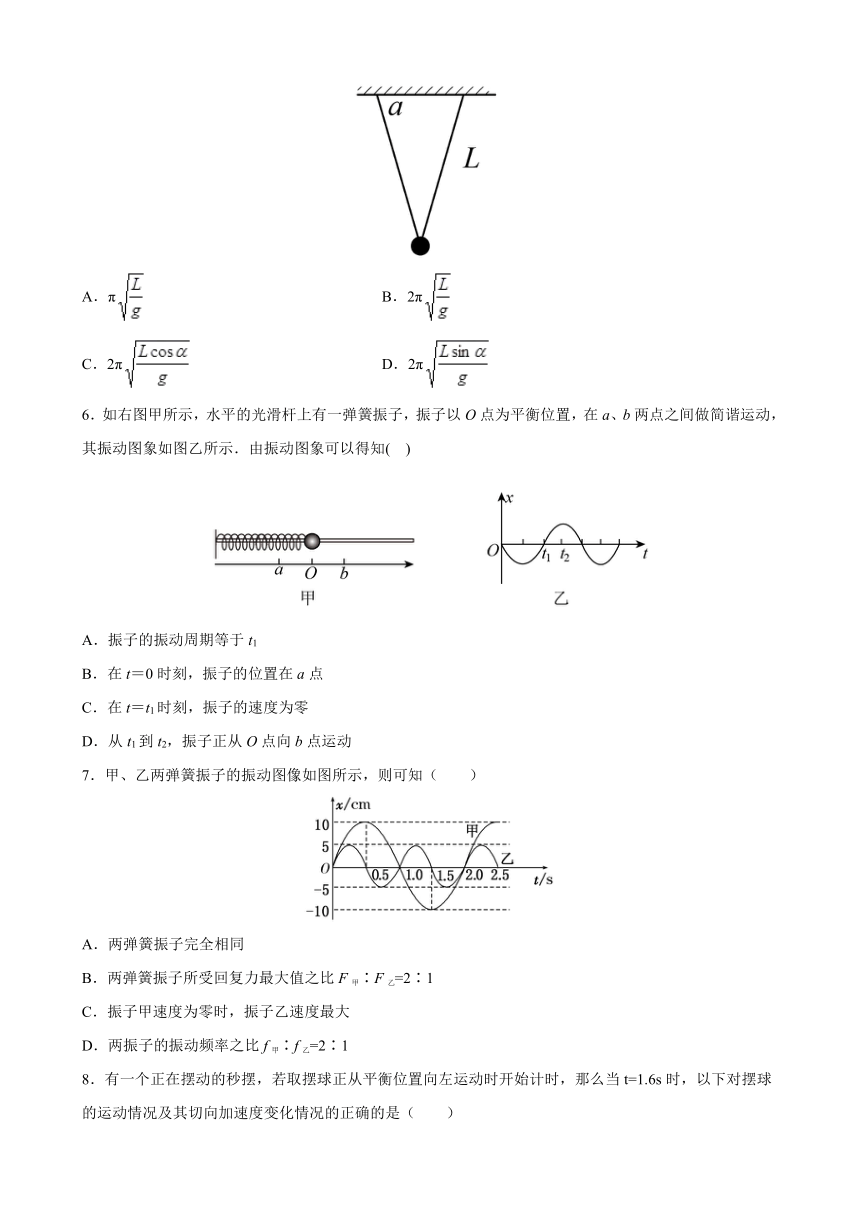
5.如图所示,用两根等长的轻线悬挂一个小球,设绳长L和角α已知,当小球垂直于纸面做简谐运动时,其周期表达式为
A.π B.2π
C.2π D.2π
6.如右图甲所示,水平的光滑杆上有一弹簧振子,振子以O点为平衡位置,在a、b两点之间做简谐运动,其振动图象如图乙所示.由振动图象可以得知( )
A.振子的振动周期等于t1
B.在t=0时刻,振子的位置在a点
C.在t=t1时刻,振子的速度为零
D.从t1到t2,振子正从O点向b点运动
7.甲、乙两弹簧振子的振动图像如图所示,则可知( )
A.两弹簧振子完全相同
B.两弹簧振子所受回复力最大值之比F甲∶F乙=2∶1
C.振子甲速度为零时,振子乙速度最大
D.两振子的振动频率之比f甲∶f乙=2∶1
8.有一个正在摆动的秒摆,若取摆球正从平衡位置向左运动时开始计时,那么当t=1.6s时,以下对摆球的运动情况及其切向加速度变化情况的正确的是( )
A.正在向左做减速运动,加速度正在增大 B.正在向右做减速运动,加速度正在增大
C.正在向左做加速运动,加速度正在减小 D.正在向右做加速运动,加速度正在减小
二、多选题
9.下列关于机械振动的有关说法正确的是( )
A.简谐运动的回复力是按效果命名的力
B.振动图像描述的是振动质点的轨迹
C.受迫振动的频率等于驱动力的频率
D.当驱动力的频率等于受迫振动系统的固有频率时,振幅最大
10.下列说法正确的是( )
A.受迫振动系统在非共振状态时,同一振幅对应的驱动力频率一定有两个
B.简谐运动平衡位置一定是运动过程的中心位置,但不一定处于平衡状态
C.简谐运动的图像描述的是振动质点的轨迹
D.弹簧振子每次经过平衡位置时的动能最大,弹性势能为零
11.如图,一列简谐横波在均匀介质中沿+x轴方向传播,其波长为λ、周期为T。某时刻,在该波传播方向上的P、Q两质点(图中未画出,P点比Q点更靠近波源)偏离各自平衡位置的位移大小相等、方向相反,则下列说法正确的是( )
A.P、Q两质点平衡位置间的距离可能等于
B.此时刻P、Q两质点的速度可能相同
C.波从P点传到Q点所需时间可能等于一个周期
D.P、Q两质点平衡位置间的距离可能介于和λ之间
12.如图所示,有一个摆长为l的单摆,现将摆球A拉离平衡位置一个很小的角度,然后由静止释放,A摆至平衡位置P时,恰与静止在P处的B球发生碰撞,碰后A继续向右摆动,B球以速度v沿光滑水平面向右运动,与右侧的墙壁碰撞后以原速率返回,当B球重新回到位置P时能与A再次相遇,则位置P与墙壁间的距离d可能为( )
A. B.
C. D.
三、填空题
13.如图所示,三角架质量为M,沿其中轴线用两根轻弹簧拴一质量为m的小球,原来三角架静止在水平面上.现使小球做上下振动,已知三角架对水平面的压力最小为零,求:(重力加速度为g)
(1)此时小球的瞬时加速度_____
(2)若上、下两弹簧的劲度系数均为k,则小球做简谐运动的振幅为_____________
14.质点做简谐运动的周期为0.4s,振幅为0.1m,从质点通过平衡位置开始计时,则经5s,质点通过的路程等于________m,位移为________m,5s末质点的加速度为________。
15.如图所示,一弹簧振子沿光滑水平杆在BC间做简谐运动,O为平衡位置,振幅。从振子经过图中B点时开始计时,经时间0.1s第一次到达O点,则振子的振动周期________;取向右方向为正方向,振子振动方程的表达式________。
16.某同学在用单摆测量重力加速度的实验中,先测得摆线长为97.50cm,摆球直径为2.00cm,然后用停表记录了单摆振动50次所用的时间。
(1)该单摆摆长为___________cm;
(2)如果他测得的g值偏小,可能的原因是___________;
A.测摆线长时读数有误,使摆长测量值偏大
B.摆线上端未牢固地系于悬点,振动中出现松动,使周期测量值变大了
C.开始计时时,停表过迟按下
D.实验中误将49次全振动次数记为50次
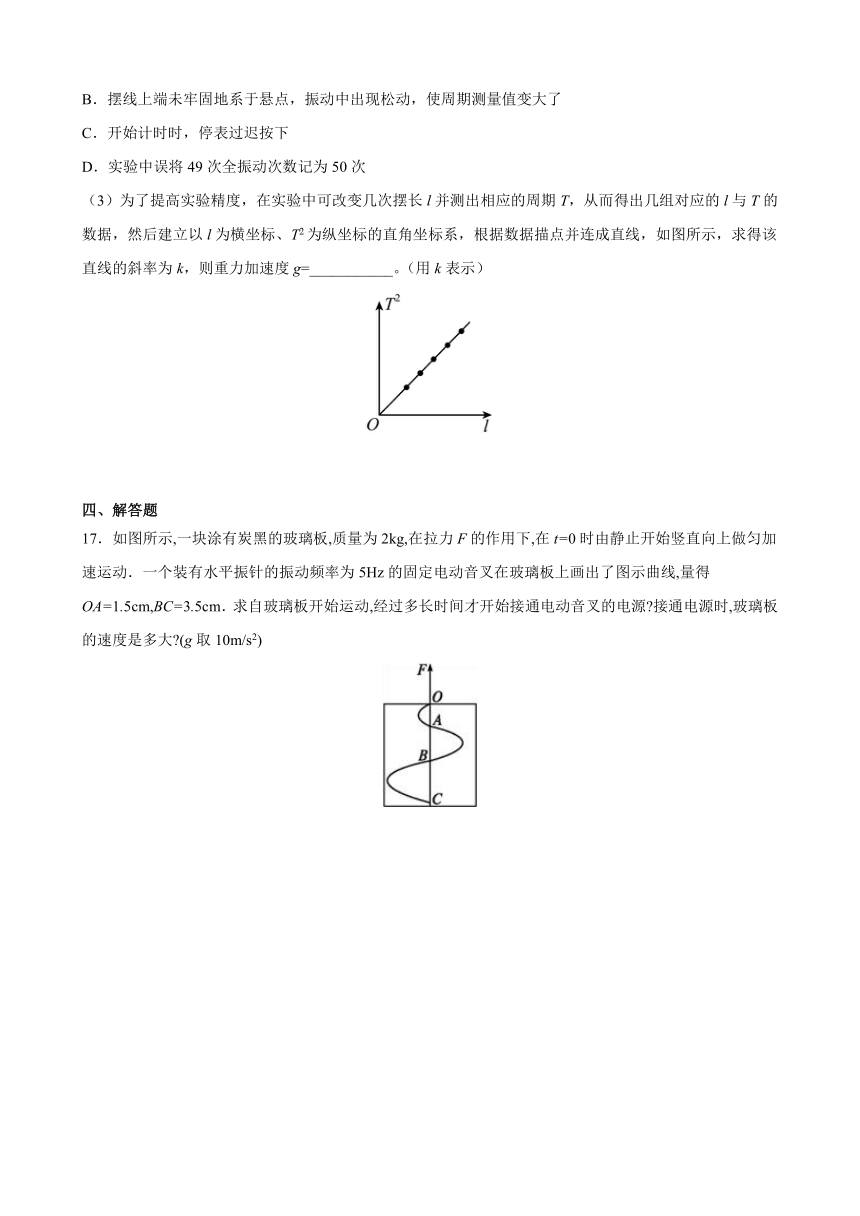
(3)为了提高实验精度,在实验中可改变几次摆长l并测出相应的周期T,从而得出几组对应的l与T的数据,然后建立以l为横坐标、T2为纵坐标的直角坐标系,根据数据描点并连成直线,如图所示,求得该直线的斜率为k,则重力加速度g=___________。(用k表示)
四、解答题
17.如图所示,一块涂有炭黑的玻璃板,质量为2kg,在拉力F的作用下,在t=0时由静止开始竖直向上做匀加速运动.一个装有水平振针的振动频率为5Hz的固定电动音叉在玻璃板上画出了图示曲线,量得OA=1.5cm,BC=3.5cm.求自玻璃板开始运动,经过多长时间才开始接通电动音叉的电源 接通电源时,玻璃板的速度是多大 (g取10m/s2)
18.如图所示,摆长为L的单摆竖直悬挂后摆球在最低点O距离地面高度为h,现将摆球拉至A点无初速度释放,摆角为θ(θ<5°).当摆球运动到最低点O时,摆线突然断裂.不计空气阻力,重力加速度为g,求摆球从A点开始运动到落地经历的时间.
19.如图所示为一弹簧振子的振动图象,试完成以下问题:
(1)写出该振子简谐运动的表达式.
(2)在第2s末到第3s末这段时间内,弹簧振子的加速度、速度、动能和弹性势能各是怎样变化的?
(3)该振子在前100s的总位移是多少?路程是多少?
20.如图所示为一列简谐横波在t=0时刻的图象。此时质点P的运动方向沿y轴负方向,且当t=0.55s时质点P恰好第3次到达y轴正方向最大位移处。问:
(1)该简谐横波的波速v的大小和方向如何?
(2)从t=0至t=1.2s,质点Q运动的路程L是多少?
(3)当t=1.2s时,质点Q相对于平衡位置的位移大小是多少?
参考答案
1.B
【解析】将一个单摆由甲地移到乙地后,发现摆钟变快了,知周期变短了,通过单摆的周期公式分析原因和增大周期的方法.
根据单摆的周期公式,知摆钟变快了,则周期变短了,说明乙地的重力加速度大于甲地的重力加速度,即,为了增大周期,可以增大摆长,B正确.
2.C
【解析】根据加速度与位移方向相反,读出加速度的方向.分析位移的变化,确定速度方向及其变化.根据质点的位置,分析加速度和速度的大小.
在t=4s时质点位于最大位移处,速度为0,加速度最大,故A错误;在t=1s时,质点通过平衡位置,速度最大,而加速度为0,故B错误;在0到1s时间内,质点的速度沿负方向,位移为正方向,由知,加速度沿负方向,则两者方向相同,C正确;在t=2s时,质点的位移沿x轴负方向,根据知,加速度沿x轴正方向,故D错误.
3.A
【分析】
根据振动图象判断质点振动方向的方法:沿着时间轴看去,“上坡”段质点向上振动,“下坡”段质点向下振动.
【解析】AC.在t=1 s和t=3 s时,振子偏离平衡位置最远,速度为零,回复力最大,加速度最大,方向指向平衡位置,A正确,C错误;
BD.在t=2 s和t=4 s时,振子位于平衡位置,速度最大,回复力和加速度均为零,BD错误.
4.D
【解析】若振子开始运动的方向先向左,再向M点运动,运动路线如图a所示,
质点从O到a再b的时间为,于是得振动的周期为,振子第三次通过M点需要经过的时间为.
若振子开始运动的方向向右直接向M点运动,如图b所示,
振动的周期为T=1.6s,振子第三次通过M点需要经过的时间为t=T﹣0.2s=1.4s
考点:简谐运动的振幅、周期和频率及简谐运动的对称性.
5.D
【解析】如图所示,由于小球垂直于纸面做简谐运动,所以等效摆长为Lsinα,由于小球做简谐运动,所以单摆的振动周期为:,故D正确.
考点:本题考查单摆的振动周期以及等效摆长的求法.
6.D
【解析】A中振子的振动周期等于2t1,故A不对;B中在t=0时刻,振子的位置在O点,然后向左运动,故B不对;C中在t=t1时刻,振子经过平衡位置,此时它的速度最大,故C不对;D中从t1到t2,振子正从O点向b点运动,故D是正确的.
7.C
【解析】A.由于两振子的振动周期不同,所以频率不同,故相位不同,A错误;
B.由振动图像读出两振子位移最大值之比,根据简谐运动的特征,由于弹簧的劲度系数k可能不等,回复力最大值之比不一定等于。故B错误;
C.甲在最大位移处时,乙在平衡位置,所以甲的速度为0时,乙的速度最大,C正确;
D.从图中可知,故,D错误。
故选C。
8.C
【解析】秒摆的周期为2s,在时,摆球经过了四分之三个周期,已经经过平衡位置,加速度增大,速度减小,C对;
9.ACD
【解析】A.简谐运动的回复力是按效果命名的力,故A正确;
B.振动图像描述的是振动质点在不同时刻的位移,而不是其实际的运动轨迹,故B错误;
C.物体在周期性驱动力作用下做受迫振动,受迫振动的频率等于驱动力的频率,与固有频率无关故C正确;
D.当驱动力的频率等于受迫振动系统的固有频率时,发生共振,振幅达到最大,故D正确。
故选ACD。
10.AB
【解析】A.根据受迫振动的特点以及振动图像可知,当驱动力频率等于物体的固有频率时,物体的振幅最大,而在非共振状态时,同一振幅对应的驱动力的频率一定有两个,如图,故A正确。
B.平衡位置是回复力为零的位置,一定是运动过程的中心位置,但物体的合外力未必为零,物体不一定处于平衡状态,例如单摆摆动经过平衡位置时,虽然回复力为零,但合力不为零,而是合力指向圆心,提供圆周运动的向心力,不处于平衡状态,选项B正确。
C.简谐运动的图像描述的是振动质点在不同时刻离开平衡位置的位移,不是振动质点的轨迹,选项C错误;
D.弹簧振子每次经过平衡位置时的动能最大,但是弹性势能不一定为零,例如竖直放置的弹簧振子,选项D错误。
故选AB。
11.ABD
【解析】AD.依题,某时刻P、Q两质点的位移大小相等、方向相反,它们可能是反相点,振动情况总是相反,也可能不是,所以P、Q两质点间的距离可能等于半个波长,也可能不等于半个波长,故AD正确;
B.根据波形分析得知,此时刻P、Q两质点的速度方向可能相反,也可能相同,故B正确;
C.若PQ间距离等于一个波长,波从P点传到Q点所需时间等于一个周期,而P、Q的位移大小相等,方向相反,PQ间距离不可能等于一个波长,所以波从P点传到Q点所需时间不可能等于一个周期,故C错误;
故选ABD。
12.BD
【解析】摆球A做简谐运动,当其与B球发生碰撞后速度改变,但是摆动的周期不变.而B球做匀速直线运动,再次相遇的条件为B球来回所需要的时间为单摆半周期的整数倍.
B球运动时间
(n=1,2,3……)①
B球做匀速直线运动,运动时间
②
单摆周期公式
③
联立①②③解得
(n=1,2,3……)
当n=1时
当n=2时
当n=3时
故BD正确,AC错误。
故选BD。
13.
【解析】(1)小球运动到最高点时,三角架对水平面的压力最小为零,此时对整体根据牛顿第二定律,有
(M+m)g=ma
解得
向下
(2)小球做简谐运动,根据回复力公式F=kx,有
2k A=ma
解得
14.5 0 0
【解析】质点运动的时间
,
因为从平衡位置开始振动,所以在5s内振子通过的路程为
经过5s,振子又回到了平衡位置,所以位移为0
经过5s,振子又回到了平衡位置,所以加速度为0
15.0.4
【解析】 从振子经过图中B点时开始计时,经时间0.1s第一次到达O点,则周期为
T=0.1×4s=0.4s
从负向最大位移处开始计时,其位移时间关系公式为
16.98.50 B
【解析】(1) 单摆摆长等于摆线长加摆球的半径,即
l=l'+=98.50cm
(2)由单摆周期公式
得
所以l偏大,则g偏大;t偏小,则g偏大;t偏大,则g偏小;n偏大,则g偏大。
ACD错误,B正确。
故选B。
(3)由单摆周期公式可得
那么题图中直线斜率
k=
所以
17.0.1s;0.1m/s
【解析】
【解析】设玻璃板竖直向上运动的加速度为a,则有:
其中:
解得
;
根据匀变速运动的推论,知:
则打A点时玻璃板的速度为
接通电源时,玻璃板的速度是
根据速度时间关系公式,有,解得
即自玻璃板开始运动,经0.1s时间才开始接通电动音叉电源.
18.
【解析】根据单摆的周期公式求出摆球从A运动到O点的时间,摆线突然断裂后,摆球做平抛运动,根据高度求出平抛运动的时间,两者之和即为总时间
单摆的周期
摆线断裂后,由
得下落时间
则
19.(1)该振子简谐运动的表达式x="Asinωt=5sin0.5πt" cm.
(2)在第2s末到第3s末这段时间内,弹簧振子的位移负向逐渐增大,速度减小,动能减小,弹性势能增大,加速度逐渐增大
(3)该振子在前100s的总位移为零,路程为5m
【解析】(1)弹簧振子的周期为 T=4s,则公式ω==0.5π rad/s;振幅 A=5cm故该振子简谐运动的表达式为 x=Asinωt=5sin0.5πt cm.
(2)第2s末到第3s末这段时间内,据图可知,振子的位移负向逐渐增大,速度减小,动能减小,弹性势能增大,加速度逐渐增大;当3s末时,振子的位移最大,加速度最大,速度为零,动能为零,弹性势能最大.
(3)因n===25,而振子在一个周期内通过的路程是4A,所以振子在前100s的总路程是:S=25×4A=100×5cm=500cm=5m;总位移为0.
答:(1)该振子简谐运动的表达式x=Asinωt=5sin0.5πt cm.
(2)在第2s末到第3s末这段时间内,弹簧振子的位移负向逐渐增大,速度减小,动能减小,弹性势能增大,加速度逐渐增大
(3)该振子在前100s的总位移为零,路程为5m.
20.(1)2m/s,波沿x轴负向传播;(2)120cm;(3)2.5cm
【解析】(1)此时质点P的运动方向沿y轴负方向,则此波沿x轴负向传播。
在到这段时间里,质点P恰好第3次到达y正方向最大位移处,则
解得
由图象可得简谐波的波长为,则波速
(2)在t=0至t=1.2s这段时间,质点Q恰经过了6个周期,所以这段时间内质点Q运动的路程为
(3)在t=0至t=1.2s这段时间,质点Q恰经过了6个周期,则t=1.2s时质点Q相对于平衡位置的位移大小等于t=0时质点Q相对于平衡位置的位移大小,为2.5cm。
一、单选题
1.一单摆由甲地移到乙地后,发现走时变快了,其变快的原因及调整的方法是( )
A.g甲>g乙,将摆长缩短
B.g甲
2.如图为某质点沿x轴做简谐运动的图象,下列说法中正确的是( )
A.在t=4s时质点速度最大,加速度为0
B.在t=1s时,质点速度和加速度都达到最大值
C.在0到1s时间内,质点速度和加速度方向相同
D.在t=2s时,质点的位移沿x轴负方向,加速度也沿x轴负方向
3.某弹簧振子沿x轴的简谐运动图象如图所示,下列描述正确的是( )
A.t =1 s时,振子的速度为零,加速度为负的最大值
B.t =2 s时,振子的速度为负,加速度为正的最大值
C.t =3 s时,振子的速度为负的最大值,加速度为零
D.t =4 s时,振子的速度为正,加速度为负的最大值
4.弹簧振子做简谐振动,0为平衡位置,以它从0点开始运动作为计时起点,经过0.3s后第一次到达M点,再经过0.2s后第二次达达M点,则它第三次到达M点还需要经过的时间为:
①1.1s ②1.4s ③1.6s ④1/3s
A.①② B.③④ C.①③ D.②④
5.如图所示,用两根等长的轻线悬挂一个小球,设绳长L和角α已知,当小球垂直于纸面做简谐运动时,其周期表达式为
A.π B.2π
C.2π D.2π
6.如右图甲所示,水平的光滑杆上有一弹簧振子,振子以O点为平衡位置,在a、b两点之间做简谐运动,其振动图象如图乙所示.由振动图象可以得知( )
A.振子的振动周期等于t1
B.在t=0时刻,振子的位置在a点
C.在t=t1时刻,振子的速度为零
D.从t1到t2,振子正从O点向b点运动
7.甲、乙两弹簧振子的振动图像如图所示,则可知( )
A.两弹簧振子完全相同
B.两弹簧振子所受回复力最大值之比F甲∶F乙=2∶1
C.振子甲速度为零时,振子乙速度最大
D.两振子的振动频率之比f甲∶f乙=2∶1
8.有一个正在摆动的秒摆,若取摆球正从平衡位置向左运动时开始计时,那么当t=1.6s时,以下对摆球的运动情况及其切向加速度变化情况的正确的是( )
A.正在向左做减速运动,加速度正在增大 B.正在向右做减速运动,加速度正在增大
C.正在向左做加速运动,加速度正在减小 D.正在向右做加速运动,加速度正在减小
二、多选题
9.下列关于机械振动的有关说法正确的是( )
A.简谐运动的回复力是按效果命名的力
B.振动图像描述的是振动质点的轨迹
C.受迫振动的频率等于驱动力的频率
D.当驱动力的频率等于受迫振动系统的固有频率时,振幅最大
10.下列说法正确的是( )
A.受迫振动系统在非共振状态时,同一振幅对应的驱动力频率一定有两个
B.简谐运动平衡位置一定是运动过程的中心位置,但不一定处于平衡状态
C.简谐运动的图像描述的是振动质点的轨迹
D.弹簧振子每次经过平衡位置时的动能最大,弹性势能为零
11.如图,一列简谐横波在均匀介质中沿+x轴方向传播,其波长为λ、周期为T。某时刻,在该波传播方向上的P、Q两质点(图中未画出,P点比Q点更靠近波源)偏离各自平衡位置的位移大小相等、方向相反,则下列说法正确的是( )
A.P、Q两质点平衡位置间的距离可能等于
B.此时刻P、Q两质点的速度可能相同
C.波从P点传到Q点所需时间可能等于一个周期
D.P、Q两质点平衡位置间的距离可能介于和λ之间
12.如图所示,有一个摆长为l的单摆,现将摆球A拉离平衡位置一个很小的角度,然后由静止释放,A摆至平衡位置P时,恰与静止在P处的B球发生碰撞,碰后A继续向右摆动,B球以速度v沿光滑水平面向右运动,与右侧的墙壁碰撞后以原速率返回,当B球重新回到位置P时能与A再次相遇,则位置P与墙壁间的距离d可能为( )
A. B.
C. D.
三、填空题
13.如图所示,三角架质量为M,沿其中轴线用两根轻弹簧拴一质量为m的小球,原来三角架静止在水平面上.现使小球做上下振动,已知三角架对水平面的压力最小为零,求:(重力加速度为g)
(1)此时小球的瞬时加速度_____
(2)若上、下两弹簧的劲度系数均为k,则小球做简谐运动的振幅为_____________
14.质点做简谐运动的周期为0.4s,振幅为0.1m,从质点通过平衡位置开始计时,则经5s,质点通过的路程等于________m,位移为________m,5s末质点的加速度为________。
15.如图所示,一弹簧振子沿光滑水平杆在BC间做简谐运动,O为平衡位置,振幅。从振子经过图中B点时开始计时,经时间0.1s第一次到达O点,则振子的振动周期________;取向右方向为正方向,振子振动方程的表达式________。
16.某同学在用单摆测量重力加速度的实验中,先测得摆线长为97.50cm,摆球直径为2.00cm,然后用停表记录了单摆振动50次所用的时间。
(1)该单摆摆长为___________cm;
(2)如果他测得的g值偏小,可能的原因是___________;
A.测摆线长时读数有误,使摆长测量值偏大
B.摆线上端未牢固地系于悬点,振动中出现松动,使周期测量值变大了
C.开始计时时,停表过迟按下
D.实验中误将49次全振动次数记为50次
(3)为了提高实验精度,在实验中可改变几次摆长l并测出相应的周期T,从而得出几组对应的l与T的数据,然后建立以l为横坐标、T2为纵坐标的直角坐标系,根据数据描点并连成直线,如图所示,求得该直线的斜率为k,则重力加速度g=___________。(用k表示)
四、解答题
17.如图所示,一块涂有炭黑的玻璃板,质量为2kg,在拉力F的作用下,在t=0时由静止开始竖直向上做匀加速运动.一个装有水平振针的振动频率为5Hz的固定电动音叉在玻璃板上画出了图示曲线,量得OA=1.5cm,BC=3.5cm.求自玻璃板开始运动,经过多长时间才开始接通电动音叉的电源 接通电源时,玻璃板的速度是多大 (g取10m/s2)
18.如图所示,摆长为L的单摆竖直悬挂后摆球在最低点O距离地面高度为h,现将摆球拉至A点无初速度释放,摆角为θ(θ<5°).当摆球运动到最低点O时,摆线突然断裂.不计空气阻力,重力加速度为g,求摆球从A点开始运动到落地经历的时间.
19.如图所示为一弹簧振子的振动图象,试完成以下问题:
(1)写出该振子简谐运动的表达式.
(2)在第2s末到第3s末这段时间内,弹簧振子的加速度、速度、动能和弹性势能各是怎样变化的?
(3)该振子在前100s的总位移是多少?路程是多少?
20.如图所示为一列简谐横波在t=0时刻的图象。此时质点P的运动方向沿y轴负方向,且当t=0.55s时质点P恰好第3次到达y轴正方向最大位移处。问:
(1)该简谐横波的波速v的大小和方向如何?
(2)从t=0至t=1.2s,质点Q运动的路程L是多少?
(3)当t=1.2s时,质点Q相对于平衡位置的位移大小是多少?
参考答案
1.B
【解析】将一个单摆由甲地移到乙地后,发现摆钟变快了,知周期变短了,通过单摆的周期公式分析原因和增大周期的方法.
根据单摆的周期公式,知摆钟变快了,则周期变短了,说明乙地的重力加速度大于甲地的重力加速度,即,为了增大周期,可以增大摆长,B正确.
2.C
【解析】根据加速度与位移方向相反,读出加速度的方向.分析位移的变化,确定速度方向及其变化.根据质点的位置,分析加速度和速度的大小.
在t=4s时质点位于最大位移处,速度为0,加速度最大,故A错误;在t=1s时,质点通过平衡位置,速度最大,而加速度为0,故B错误;在0到1s时间内,质点的速度沿负方向,位移为正方向,由知,加速度沿负方向,则两者方向相同,C正确;在t=2s时,质点的位移沿x轴负方向,根据知,加速度沿x轴正方向,故D错误.
3.A
【分析】
根据振动图象判断质点振动方向的方法:沿着时间轴看去,“上坡”段质点向上振动,“下坡”段质点向下振动.
【解析】AC.在t=1 s和t=3 s时,振子偏离平衡位置最远,速度为零,回复力最大,加速度最大,方向指向平衡位置,A正确,C错误;
BD.在t=2 s和t=4 s时,振子位于平衡位置,速度最大,回复力和加速度均为零,BD错误.
4.D
【解析】若振子开始运动的方向先向左,再向M点运动,运动路线如图a所示,
质点从O到a再b的时间为,于是得振动的周期为,振子第三次通过M点需要经过的时间为.
若振子开始运动的方向向右直接向M点运动,如图b所示,
振动的周期为T=1.6s,振子第三次通过M点需要经过的时间为t=T﹣0.2s=1.4s
考点:简谐运动的振幅、周期和频率及简谐运动的对称性.
5.D
【解析】如图所示,由于小球垂直于纸面做简谐运动,所以等效摆长为Lsinα,由于小球做简谐运动,所以单摆的振动周期为:,故D正确.
考点:本题考查单摆的振动周期以及等效摆长的求法.
6.D
【解析】A中振子的振动周期等于2t1,故A不对;B中在t=0时刻,振子的位置在O点,然后向左运动,故B不对;C中在t=t1时刻,振子经过平衡位置,此时它的速度最大,故C不对;D中从t1到t2,振子正从O点向b点运动,故D是正确的.
7.C
【解析】A.由于两振子的振动周期不同,所以频率不同,故相位不同,A错误;
B.由振动图像读出两振子位移最大值之比,根据简谐运动的特征,由于弹簧的劲度系数k可能不等,回复力最大值之比不一定等于。故B错误;
C.甲在最大位移处时,乙在平衡位置,所以甲的速度为0时,乙的速度最大,C正确;
D.从图中可知,故,D错误。
故选C。
8.C
【解析】秒摆的周期为2s,在时,摆球经过了四分之三个周期,已经经过平衡位置,加速度增大,速度减小,C对;
9.ACD
【解析】A.简谐运动的回复力是按效果命名的力,故A正确;
B.振动图像描述的是振动质点在不同时刻的位移,而不是其实际的运动轨迹,故B错误;
C.物体在周期性驱动力作用下做受迫振动,受迫振动的频率等于驱动力的频率,与固有频率无关故C正确;
D.当驱动力的频率等于受迫振动系统的固有频率时,发生共振,振幅达到最大,故D正确。
故选ACD。
10.AB
【解析】A.根据受迫振动的特点以及振动图像可知,当驱动力频率等于物体的固有频率时,物体的振幅最大,而在非共振状态时,同一振幅对应的驱动力的频率一定有两个,如图,故A正确。
B.平衡位置是回复力为零的位置,一定是运动过程的中心位置,但物体的合外力未必为零,物体不一定处于平衡状态,例如单摆摆动经过平衡位置时,虽然回复力为零,但合力不为零,而是合力指向圆心,提供圆周运动的向心力,不处于平衡状态,选项B正确。
C.简谐运动的图像描述的是振动质点在不同时刻离开平衡位置的位移,不是振动质点的轨迹,选项C错误;
D.弹簧振子每次经过平衡位置时的动能最大,但是弹性势能不一定为零,例如竖直放置的弹簧振子,选项D错误。
故选AB。
11.ABD
【解析】AD.依题,某时刻P、Q两质点的位移大小相等、方向相反,它们可能是反相点,振动情况总是相反,也可能不是,所以P、Q两质点间的距离可能等于半个波长,也可能不等于半个波长,故AD正确;
B.根据波形分析得知,此时刻P、Q两质点的速度方向可能相反,也可能相同,故B正确;
C.若PQ间距离等于一个波长,波从P点传到Q点所需时间等于一个周期,而P、Q的位移大小相等,方向相反,PQ间距离不可能等于一个波长,所以波从P点传到Q点所需时间不可能等于一个周期,故C错误;
故选ABD。
12.BD
【解析】摆球A做简谐运动,当其与B球发生碰撞后速度改变,但是摆动的周期不变.而B球做匀速直线运动,再次相遇的条件为B球来回所需要的时间为单摆半周期的整数倍.
B球运动时间
(n=1,2,3……)①
B球做匀速直线运动,运动时间
②
单摆周期公式
③
联立①②③解得
(n=1,2,3……)
当n=1时
当n=2时
当n=3时
故BD正确,AC错误。
故选BD。
13.
【解析】(1)小球运动到最高点时,三角架对水平面的压力最小为零,此时对整体根据牛顿第二定律,有
(M+m)g=ma
解得
向下
(2)小球做简谐运动,根据回复力公式F=kx,有
2k A=ma
解得
14.5 0 0
【解析】质点运动的时间
,
因为从平衡位置开始振动,所以在5s内振子通过的路程为
经过5s,振子又回到了平衡位置,所以位移为0
经过5s,振子又回到了平衡位置,所以加速度为0
15.0.4
【解析】 从振子经过图中B点时开始计时,经时间0.1s第一次到达O点,则周期为
T=0.1×4s=0.4s
从负向最大位移处开始计时,其位移时间关系公式为
16.98.50 B
【解析】(1) 单摆摆长等于摆线长加摆球的半径,即
l=l'+=98.50cm
(2)由单摆周期公式
得
所以l偏大,则g偏大;t偏小,则g偏大;t偏大,则g偏小;n偏大,则g偏大。
ACD错误,B正确。
故选B。
(3)由单摆周期公式可得
那么题图中直线斜率
k=
所以
17.0.1s;0.1m/s
【解析】
【解析】设玻璃板竖直向上运动的加速度为a,则有:
其中:
解得
;
根据匀变速运动的推论,知:
则打A点时玻璃板的速度为
接通电源时,玻璃板的速度是
根据速度时间关系公式,有,解得
即自玻璃板开始运动,经0.1s时间才开始接通电动音叉电源.
18.
【解析】根据单摆的周期公式求出摆球从A运动到O点的时间,摆线突然断裂后,摆球做平抛运动,根据高度求出平抛运动的时间,两者之和即为总时间
单摆的周期
摆线断裂后,由
得下落时间
则
19.(1)该振子简谐运动的表达式x="Asinωt=5sin0.5πt" cm.
(2)在第2s末到第3s末这段时间内,弹簧振子的位移负向逐渐增大,速度减小,动能减小,弹性势能增大,加速度逐渐增大
(3)该振子在前100s的总位移为零,路程为5m
【解析】(1)弹簧振子的周期为 T=4s,则公式ω==0.5π rad/s;振幅 A=5cm故该振子简谐运动的表达式为 x=Asinωt=5sin0.5πt cm.
(2)第2s末到第3s末这段时间内,据图可知,振子的位移负向逐渐增大,速度减小,动能减小,弹性势能增大,加速度逐渐增大;当3s末时,振子的位移最大,加速度最大,速度为零,动能为零,弹性势能最大.
(3)因n===25,而振子在一个周期内通过的路程是4A,所以振子在前100s的总路程是:S=25×4A=100×5cm=500cm=5m;总位移为0.
答:(1)该振子简谐运动的表达式x=Asinωt=5sin0.5πt cm.
(2)在第2s末到第3s末这段时间内,弹簧振子的位移负向逐渐增大,速度减小,动能减小,弹性势能增大,加速度逐渐增大
(3)该振子在前100s的总位移为零,路程为5m.
20.(1)2m/s,波沿x轴负向传播;(2)120cm;(3)2.5cm
【解析】(1)此时质点P的运动方向沿y轴负方向,则此波沿x轴负向传播。
在到这段时间里,质点P恰好第3次到达y正方向最大位移处,则
解得
由图象可得简谐波的波长为,则波速
(2)在t=0至t=1.2s这段时间,质点Q恰经过了6个周期,所以这段时间内质点Q运动的路程为
(3)在t=0至t=1.2s这段时间,质点Q恰经过了6个周期,则t=1.2s时质点Q相对于平衡位置的位移大小等于t=0时质点Q相对于平衡位置的位移大小,为2.5cm。
同课章节目录
- 第1章 动量及其守恒定律
- 第1节 动量和动量定理
- 第2节 动量守恒定律及其应用
- 第3节 科学验证:动量守恒定律
- 第4节 弹性碰撞与非弹性碰撞
- 第2章 机械振动
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 科学测量:用单摆测量重力加速度
- 第5节 生活中的振动
- 第3章 机械波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第4章 光的折射和全反射
- 第1节 光的折射
- 第2节 科学测量:玻璃的折射率
- 第3节 光的全反射
- 第4节 光导纤维及其应用
- 第5章 光的干涉、衍射和偏振
- 第1节 光的干涉
- 第2节 科学测量:用双缝干涉测光的波长
- 第3节 光的衍射
- 第4节 光的偏振
- 第5节 激光与全息照相
