沪科版数学七年级上册 3.4 二元一次方程组的应用 课件(共15张PPT)
文档属性
| 名称 | 沪科版数学七年级上册 3.4 二元一次方程组的应用 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-19 14:34:28 | ||
图片预览





文档简介
(共15张PPT)
3.4 二元一次方程组的应用
1、下列方程组各选择哪种消元法来解比较简便
代入消元法
加减消元法
加减消元法
(1) y=2x
3x-4y=5
(2) 2x+3y=21
2x-5y=5
(3) 9x-5y=1
7y-9x=2
第一环节:复习引入
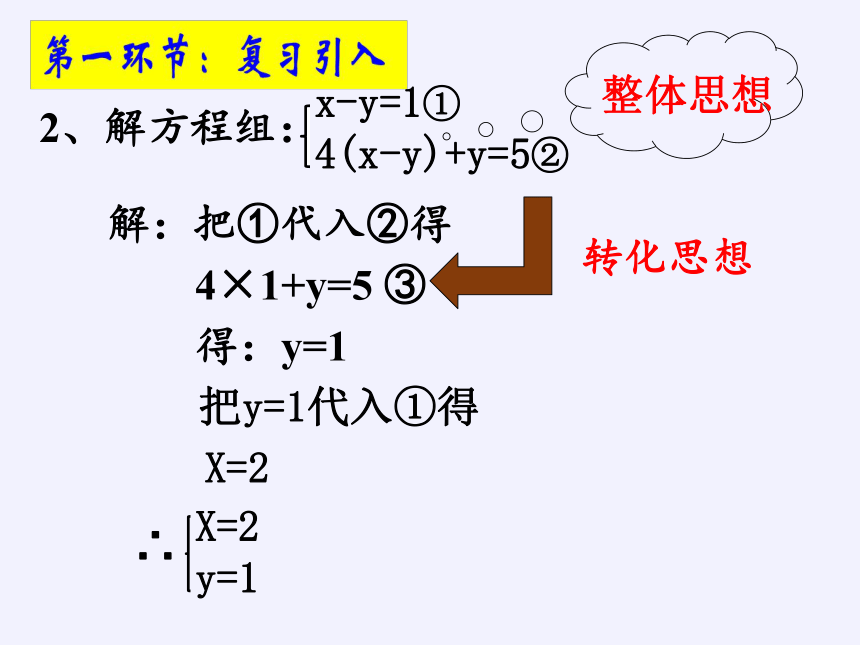
2、解方程组:
x-y=1①
4(x-y)+y=5②
解:把①代入②得
4×1+y=5 ③
得:y=1
把y=1代入①得
X=2
X=2
y=1
∴
整体思想
转化思想
方程思想
【活动一 】已知2本本子,3支铅笔共需要7元钱;3本本子,2支铅笔共需8元钱;则一本本子和一支铅笔共需要多少钱?
解:设一本本子x元,一支铅笔y元,由题意得:
①+②得
5(x+y)=15
∴x+y=3
答:一本本子和一支铅笔共需要3元钱.
、整体思想
方程思想:是指从分析问题的数量关系入手,将问题中的已知量和未知量之间的数量关系通过适当设元建立起方程(组),然后通过解方程(组)使问题得到解决的思维方式 。
小结:当一个问题中,未知数较多,一个一个求比较复杂,或有时不能求解时,可将其中满足某一共同特征的代数式看作一个整体,这样会更加简便。
一个鸡蛋、两个鸭蛋、三个鹅蛋共11元;
三个鸡蛋、两个鸭蛋、一个鹅蛋共9元.
那么:一个鸡蛋、一个鸭蛋、一个鹅蛋共需要多少钱?
解:一个鸡蛋x元,一个鸭蛋y元、一个鹅蛋
z元,由题意得:
x+2y+3z=11①
3x+2y+z=9 ②
①+②得
4(x+y+z)=20
∴x+y+z=5
即:一个鸡蛋、一个鸭蛋、
一个鹅蛋共需要5元钱
数形结合思想
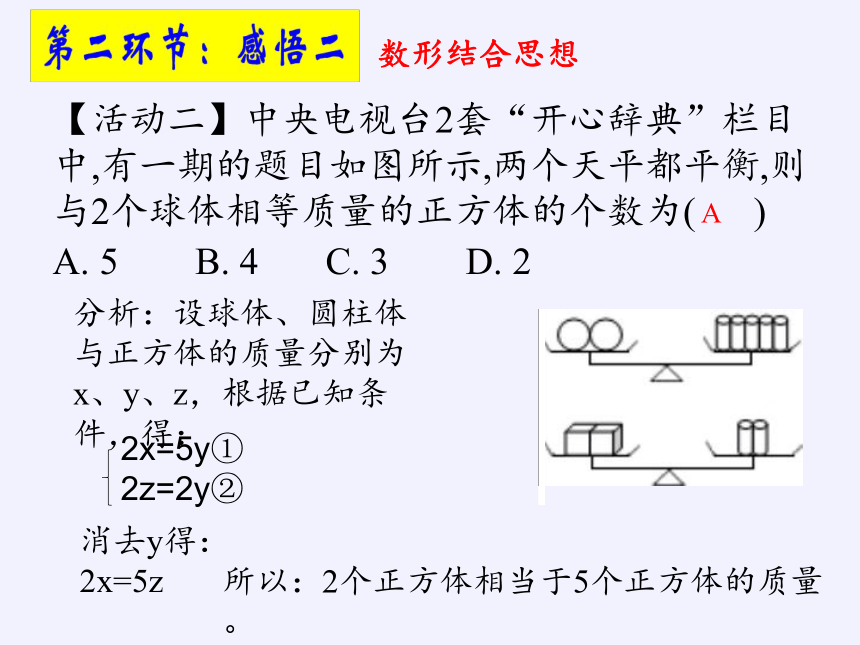
【活动二】中央电视台2套“开心辞典”栏目中,有一期的题目如图所示,两个天平都平衡,则与2个球体相等质量的正方体的个数为( )
分析:设球体、圆柱体与正方体的质量分别为x、y、z,根据已知条件,得:
2x=5y①
2z=2y②
A. 5 B. 4 C. 3 D. 2
消去y得:2x=5z
所以:2个正方体相当于5个正方体的质量。
A
小结:数形结合思想是把图形与蕴含的数量关系巧妙的结合起来,使问题更直观,更容易解决。
分类讨论思想
某通讯器材商场,计划从一厂家购进若干部新型手机以满足市场需求,已知该厂家生产三种不同型号的手机,各型号的手机出厂价如下表所示。若商场用6万元同时购进两种不同型号的手机共40部,并恰好将钱用完.请你帮助该商场设计进货方案。
型 号 A B C
出厂价(元) 1800 600 1200
、建模思想
解:设A型手机a部,B型手机b部,C型手机c部.
① A型手机a部,
B型手机b部
a+b=40
1800a+600b=60000
a=30
b=10
解得:
②A型手机a部,
C型手机c部
a+c=40
1800a+1200c=60000
a=20
c=20
解得:
③B型手机b部,C型手机c部
b+c=40
600b+1200c=60000
b=-20
c=60
解得:
(不合题意,
舍去)
综合①②③共有两种购买方案:A型30部,B型10部;或A型20部,C型20部;
小结:分类讨论的思想就是把方程组在应用题中包含各种可能情况,按某一标准分成若干类,然后对每一类分别进行解决,从而达到解决整个问题的目的。
1、基本知识和技能
二元一次方程组的应用
步骤:审、设、找、列、解、验、答。
关键:列等量关系
2、基本数学思想方法
整体、数形结合、分类讨论,建模、方程、
转化、类比等思想;
谈谈你本节课的收获。
3、通过数学活动积累了一些经验,比如用方程(组)解
决实际问题时,选择合理的方案,不能脱离生活实际等。
作业:1、必做题:练习册:76页基础(二);
2、选做题:练习册81页“探究与思考”。
一旦解决了方程问题,一切问题将迎刃而解。
——笛卡尔
实际问题数学化,
数学问题等量化,
等量关系方程化。
我思故我在!
笛卡尔
数学思想是数学的灵魂,任何数学问题的解决都是数学思想作用的结果,因此正确理解和掌握数学思想是数学学习的关键。
谢 谢
3.4 二元一次方程组的应用
1、下列方程组各选择哪种消元法来解比较简便
代入消元法
加减消元法
加减消元法
(1) y=2x
3x-4y=5
(2) 2x+3y=21
2x-5y=5
(3) 9x-5y=1
7y-9x=2
第一环节:复习引入
2、解方程组:
x-y=1①
4(x-y)+y=5②
解:把①代入②得
4×1+y=5 ③
得:y=1
把y=1代入①得
X=2
X=2
y=1
∴
整体思想
转化思想
方程思想
【活动一 】已知2本本子,3支铅笔共需要7元钱;3本本子,2支铅笔共需8元钱;则一本本子和一支铅笔共需要多少钱?
解:设一本本子x元,一支铅笔y元,由题意得:
①+②得
5(x+y)=15
∴x+y=3
答:一本本子和一支铅笔共需要3元钱.
、整体思想
方程思想:是指从分析问题的数量关系入手,将问题中的已知量和未知量之间的数量关系通过适当设元建立起方程(组),然后通过解方程(组)使问题得到解决的思维方式 。
小结:当一个问题中,未知数较多,一个一个求比较复杂,或有时不能求解时,可将其中满足某一共同特征的代数式看作一个整体,这样会更加简便。
一个鸡蛋、两个鸭蛋、三个鹅蛋共11元;
三个鸡蛋、两个鸭蛋、一个鹅蛋共9元.
那么:一个鸡蛋、一个鸭蛋、一个鹅蛋共需要多少钱?
解:一个鸡蛋x元,一个鸭蛋y元、一个鹅蛋
z元,由题意得:
x+2y+3z=11①
3x+2y+z=9 ②
①+②得
4(x+y+z)=20
∴x+y+z=5
即:一个鸡蛋、一个鸭蛋、
一个鹅蛋共需要5元钱
数形结合思想
【活动二】中央电视台2套“开心辞典”栏目中,有一期的题目如图所示,两个天平都平衡,则与2个球体相等质量的正方体的个数为( )
分析:设球体、圆柱体与正方体的质量分别为x、y、z,根据已知条件,得:
2x=5y①
2z=2y②
A. 5 B. 4 C. 3 D. 2
消去y得:2x=5z
所以:2个正方体相当于5个正方体的质量。
A
小结:数形结合思想是把图形与蕴含的数量关系巧妙的结合起来,使问题更直观,更容易解决。
分类讨论思想
某通讯器材商场,计划从一厂家购进若干部新型手机以满足市场需求,已知该厂家生产三种不同型号的手机,各型号的手机出厂价如下表所示。若商场用6万元同时购进两种不同型号的手机共40部,并恰好将钱用完.请你帮助该商场设计进货方案。
型 号 A B C
出厂价(元) 1800 600 1200
、建模思想
解:设A型手机a部,B型手机b部,C型手机c部.
① A型手机a部,
B型手机b部
a+b=40
1800a+600b=60000
a=30
b=10
解得:
②A型手机a部,
C型手机c部
a+c=40
1800a+1200c=60000
a=20
c=20
解得:
③B型手机b部,C型手机c部
b+c=40
600b+1200c=60000
b=-20
c=60
解得:
(不合题意,
舍去)
综合①②③共有两种购买方案:A型30部,B型10部;或A型20部,C型20部;
小结:分类讨论的思想就是把方程组在应用题中包含各种可能情况,按某一标准分成若干类,然后对每一类分别进行解决,从而达到解决整个问题的目的。
1、基本知识和技能
二元一次方程组的应用
步骤:审、设、找、列、解、验、答。
关键:列等量关系
2、基本数学思想方法
整体、数形结合、分类讨论,建模、方程、
转化、类比等思想;
谈谈你本节课的收获。
3、通过数学活动积累了一些经验,比如用方程(组)解
决实际问题时,选择合理的方案,不能脱离生活实际等。
作业:1、必做题:练习册:76页基础(二);
2、选做题:练习册81页“探究与思考”。
一旦解决了方程问题,一切问题将迎刃而解。
——笛卡尔
实际问题数学化,
数学问题等量化,
等量关系方程化。
我思故我在!
笛卡尔
数学思想是数学的灵魂,任何数学问题的解决都是数学思想作用的结果,因此正确理解和掌握数学思想是数学学习的关键。
谢 谢
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
