人教课标版(B版)高中数学必修5《数列求和》复习 课件 (共18张PPT)
文档属性
| 名称 | 人教课标版(B版)高中数学必修5《数列求和》复习 课件 (共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 392.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 15:35:04 | ||
图片预览






文档简介
(共18张PPT)
数列 求和
学习目标
1.掌握等差数列、等比数列的前n项和公式.
2.掌握一般数列求和的几种常见的方法.
知 识 梳 理
一、公式法
1.直接利用等差数列、等比数列的前n项公式求和
(1)等差数列的前n项和公式Sn=____________
=____________ . (其中a1为首项,d为公差)
(2)等比数列的前n项和公式
当q=1时, Sn =
当q≠1时,Sn=____________=____________.(其中a1为首项,q为公比)
na1
2.一些常见数列的前n项和
(1)1+2+3+4+…+n=________________;
(2)2+4+6+…+2n=________________;
(3)1+3+5+…+2n-1=________________.
________________;
________________;
n(n+1)
n2
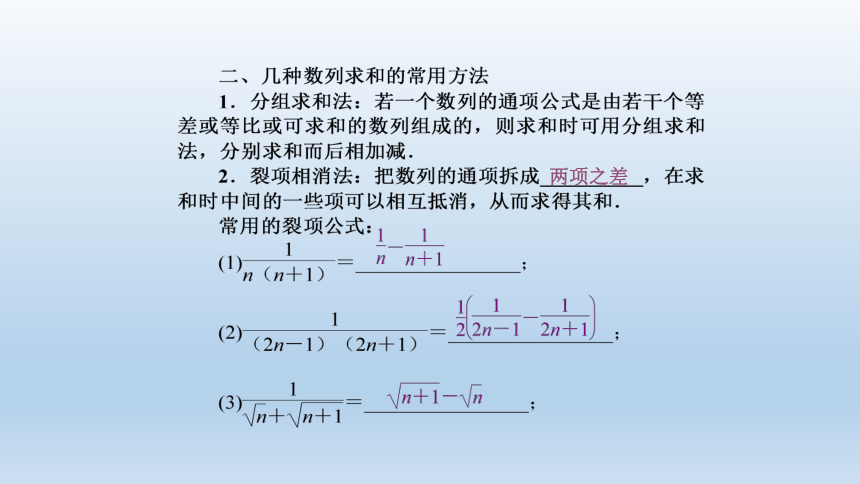
两项之差
3.错位相减法:如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的,那么这个数列的前n项和即可用错位相减法求和;
4.倒序相加法:如果一个数列{an},首末两端等“距离”的两项的和相等或等于__________,那么求这个数列的前n项和即可用倒序相加法求和.
同一个常数
考点一 累加法求通项公式
【规律·方法】 利用恒等式an=a1+(a2-a1)+…+(an-an-1)求通项公式的方法称为累加法。累加法是求型如an+1=an+f(n)的递推数列通项公式的基本方法,其中f(n)可求前n项和。
对应训练1 设数列{an}满足a1=2,an+1-an=3·22n-1(n∈N*),求数列{an}的通项公式。
解 累加法:由已知得,当n≥1时,an+1=[(an+1-an)+(an-an-1)+…+(a2-a1)]+a1=3(22n-1+22n-3+…+2)+2=22(n+1)-1。而a1=2,所以数列{an}的通项公式为an=22n-1。
考点二 累乘法求通项公式
考点三 构造法求通项公式
数列 求和
学习目标
1.掌握等差数列、等比数列的前n项和公式.
2.掌握一般数列求和的几种常见的方法.
知 识 梳 理
一、公式法
1.直接利用等差数列、等比数列的前n项公式求和
(1)等差数列的前n项和公式Sn=____________
=____________ . (其中a1为首项,d为公差)
(2)等比数列的前n项和公式
当q=1时, Sn =
当q≠1时,Sn=____________=____________.(其中a1为首项,q为公比)
na1
2.一些常见数列的前n项和
(1)1+2+3+4+…+n=________________;
(2)2+4+6+…+2n=________________;
(3)1+3+5+…+2n-1=________________.
________________;
________________;
n(n+1)
n2
两项之差
3.错位相减法:如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的,那么这个数列的前n项和即可用错位相减法求和;
4.倒序相加法:如果一个数列{an},首末两端等“距离”的两项的和相等或等于__________,那么求这个数列的前n项和即可用倒序相加法求和.
同一个常数
考点一 累加法求通项公式
【规律·方法】 利用恒等式an=a1+(a2-a1)+…+(an-an-1)求通项公式的方法称为累加法。累加法是求型如an+1=an+f(n)的递推数列通项公式的基本方法,其中f(n)可求前n项和。
对应训练1 设数列{an}满足a1=2,an+1-an=3·22n-1(n∈N*),求数列{an}的通项公式。
解 累加法:由已知得,当n≥1时,an+1=[(an+1-an)+(an-an-1)+…+(a2-a1)]+a1=3(22n-1+22n-3+…+2)+2=22(n+1)-1。而a1=2,所以数列{an}的通项公式为an=22n-1。
考点二 累乘法求通项公式
考点三 构造法求通项公式
