简单数据结构课件-2021-2022学年中学生信息学奥林匹克竞赛数据结构(难点)精讲(161张PPT)
文档属性
| 名称 | 简单数据结构课件-2021-2022学年中学生信息学奥林匹克竞赛数据结构(难点)精讲(161张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2021-12-19 11:11:29 | ||
图片预览











文档简介
(共161张PPT)
简单数据结构
信息学奥林匹克竞赛知识点(难点)讲解——数据结构【尖端】
1.序列维护(线段树&平衡树)
线段树
相信大家都会线段树了,所以就不讲原理了
平衡树
全称“平衡二叉搜索树”,常见的类型有:
1.splay
2.treap
3.AVL Tree
4.Red Black Tree
5.Scape Goat Tree
6.Weight Balanced Leafy Tree(特殊结构)
二叉搜索树
性质:一个节点x左子树所有点的关键字都比x的关键字小,右子树所有点的关键字都比x的关键字大
平衡树
限于篇幅,这里只讲一下treap和splay
treap
“树堆”“Tree + Heap”
性质:每个点随机分配一个权值,使treap同时满足堆性质和二叉搜索树性质
复杂度:期望O( logn )
treap
设每个节点的关键字是key,随机权值是rand
1.如果v是u的左儿子,则key[v] < key[u]
2.如果v是u的右儿子,则key[v] > key[u]
3.如果v是u的子节点,则rand[u] > rand[v]
treap
Treap维护权值的时候一般会把相同的权值放在同一个节点上
所以一个treap节点需要维护以下信息:
左右儿子
关键字
关键字出现次数
堆随机值
节点大小(即子树大小)
说要讲模板,这里就利用一下hzwer的吧
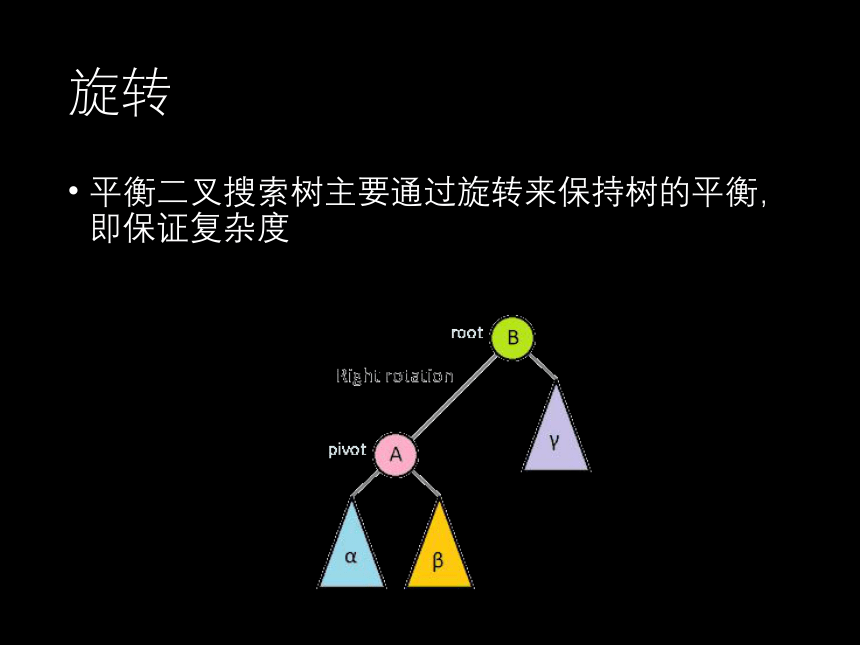
旋转
平衡二叉搜索树主要通过旋转来保持树的平衡,即保证复杂度
Treap的旋转
旋转有单旋和双旋,treap只需要单旋,这一点比较简单
Treap的插入
先给这个节点分配一个随机的堆权值
然后把这个节点按照bst的规则插入到一个叶子上:
从根节点开始,逐个判断当前节点的值与插入值的大小关系。如果插入值小于当前节点值,则递归至左儿子;大于则递归至右儿子;
然后通过旋转来调整,使得treap满足堆性质
Code
Treap的删除
和普通的BST删除一样:
如果删除值小于当前节点值,则递归至左儿子;大于则递归至右儿子
若当前节点数值的出现次数大于 1 ,则减一(通常将同一个权值缩掉)
Treap的删除
若当前节点数值的出现次数等于 1 :
若当前节点没有左儿子与右儿子,则直接删除该节点(置 0);
若当前节点没有左儿子或右儿子,则将左儿子或右儿子替代该节点;
若当前节点有左儿子与右儿子,则不断旋转当前节点,并走到当前节点新的对应位置,直到没有左儿子或右儿子为止。
Code
Treap的查询
递归到叶子节点,一路维护信息即可
Treap维护权值
现在大家都会用treap来维护一个集合
支持插入,删除,查询(kth,rank等)了吧
Treap的其他功能
Treap还可以支持维护序列时的分裂合并
这里不详细讲了(我也不会)
具体可以看luogu日报?
splay
“伸展树”“自适应查找树”
splay
每次对一个节点进行操作的时候通过一种方法把这个点旋转至根
需要根据不同的情况判断应该怎么旋转,这里就不详细介绍了
splay
Splay具有“自适应性”
大概就是说splay会根据操作的特点调整树结构,使得操作尽可能高效
可以去了解了解splay的动态最优性猜想,是个著名的open problem
Disadvantage
可以通过势能分析证明splay的复杂度是均摊O( logn )的,也就是说splay在很多次操作中可能会有一次O( n )复杂度的操作
而且这样的操作也很好构造
所以splay不适合做一些需要撤销操作/可持久化的题目(虽然可以通过随机旋转什么的方法来规避,但还是感觉很吃力)
自身常数比较大
Advantage
Splay用来维护序列还是比较好写的,用来维护名次树感觉不好写
由于自适应性,splay不需要特殊的技巧就可以高效启发式合并,还可以高效实现LCT(STT)等动态树
打个广告——WBLT
全称:Weight Balanced Leafy Tree
这个Weight Balanced是指的Balanced by Boundary,也就是BB[α]
和clj那个定义不一样
大概可以理解为通过旋转而不是重构来满足替罪羊树那个平衡关系
也就是说替罪羊树是Weight Balanced Tree的一种
打个广告——WBLT
线段树就是一种Leafy Tree,也就是说把信息都存在叶子上,非叶节点都是存储了信息的合并的虚点(大家可以感性理解一下大概是什么样的一个结构)
优点:目前最好写的平衡树,可持久化效率很高
缺点:非可持久化的情况下要两倍空间,拿来写LCT(STT)很吃力
替罪羊树
定义常数平衡因子α
如果一个点的某个儿子,占到了子树大小的α,则认为不平衡,重构这个子树
复杂度也是带均摊的,均摊O(logn),最坏单次操作O(n)
复杂度证明平凡
大概拿来解决什么样的题
给你一个序列,每次查询区间的******
给你一个树,每次查询链******
Key
是维护的可快速合并的信息,具体怎么定义快速合并比较复杂,这里不进行严谨介绍,只感性理解
Fact
其实这些题就改改线段树的merge函数之类的,相当无聊
Luogu2023 [AHOI2009]维护序列
1.区间加x
2.区间乘x
3.区间和
取膜
Problem
如果只是区间加或者区间乘,直接打个标记就可以了
但是同时有两个操作怎么办
Solution
当然是打两个标记啦,不过需要注意一下处理顺序
维护两个标记,分别是加标记和乘标记
分别设为add和mul
如果一个节点的被加上了x
则add+=x
如果一个节点被乘上了x
则add*=x,mul*=x
注意取膜
即对于标记按顺序维护
先加后乘
常见的打标记的操作
区间加
区间乘
区间染色(区间修改为一个数)
区间翻转
区间xor
Luogu4513 小白逛公园
序列,单点修改,询问区间最大子段和
Solution
著名的新手杀手题。。。
很经典来着
对于每个区间,维护一个左边的最大前缀,右边的最大后缀,以及区间内部的答案
每次合并的时候,即答案选取左子区间的max,右子区间的max,或者左子区间的最大后缀,右子区间的最大前缀即可
很简单的题
Solution
Luogu2042 [NOI2005]维护数列
请写一个程序,要求维护一个数列,支持以下 6 种操作:(请注意,格式栏 中的下划线‘ _ ’表示实际输入文件中的空格)
Solution
pushdown就维护一下区间赋值和区间翻转的标记
update就维护一下区间的最大前后缀和区间的最大子段和,然后更新就可以了
Luogu5482 [JLOI2011]不等式组
你需要维护一堆不等式
1.插入一个ax+b>c的不等式
2.删除第i个插入的
3.查询x=k的时候成立的不等式个数
Solution
如果a>0:ax+b>c x > ( c – b ) / a
如果a<0:ax+b>c x < ( c – b ) / a
如果a=0:是否成立是确定性的
开个平衡树维护值(按值域开个树状数组也行)
然后每次插入取个整
查询直接查rank即可
注意细节
Luogu1471 方差
神犇HansBug在一本数学书里面发现了一个神奇的数列,包含N个实数。他想算算这个数列的平均数和方差。
操作1:1 x y k ,表示将第x到第y项每项加上k,k为一实数。
操作2:2 x y ,表示求出第x到第y项这一子数列的平均数。
操作3:3 x y ,表示求出第x到第y项这一子数列的方差。
Solution
可以通过维护区间和来维护区间平均数
其实就是区间和/区间长度
但是方差呢?
Solution
这里直接粘一个题解里面的公式了
方差可以通过维护平方和和和的平方来算出来
很多这种题直接推推式子就可以维护了
比如SDOI那个无聊的东西
某经典问题
Solution
假设x节点的儿子为y和z
x相邻两数乘积的和为:
y相邻两数乘积的和+z相邻两数乘积的和+y最右边的数*z最左边的数
Solution
假设x节点的儿子为y和z
x任意两数乘积的和为:
y任意两数乘积的和+ z任意两数乘积的和+y的和*z的和
然后直接维护即可。。。
Luogu4198 楼房重建
有一排楼,每次把一个位置的楼的高度修改为x,每次输出可以从最左边看到的楼个数
Solution1
发现一个楼房能被看到可以等价于它的斜率比之前的任何一个都大
所以说我们这里可以直接维护斜率,而不用管楼的高度
问题转化为:
1.单点修改
2.查询全局有多少位置是前缀最大值
Solution1
可以试试分块维护
复杂度好像是O( nsqrt( nlogn ) )的
这里不仔细讲了
Solution2
考虑用线段树维护
对于线段树每个结点维护两个值:ans和max,ans表示只考虑这个区间内的可以被看到的楼房,max表示这个区间的最大楼房斜率。
如何合并区间?
Solution2
合并左右区间的时候:
显然左区间的答案不会变化
问题就是考虑右区间有多少个楼房在左区间的约束条件下仍然可以被看到
Solution2
如果右区间最大值都小于等于左区间最大值,那么右区间就没有贡献了,相当于是被整个挡住了。
Solution2
如果右区间最大值大于左区间最大值
考虑右区间的两个子区间:左子区间、右子区间
Solution2
如果左子区间的最大值小于等于左区间最大值
那么就递归处理右子区间
因为相当于左子区间里面所有楼房都被前面的楼房挡住了了,递归查询右边有多少楼房没被挡住
否则就递归处理左子区间,然后加上右子区间原本的答案,因为这个约束条件弱于左子区间对右子区间的约束,所以只考虑这个约束条件对左子区间的影响~
Solution2
由于要合并O( logn )次,每次合并会递归O( logn )个节点
所以总复杂度O( mlog^2n )
实际上常数非常小
Luogu4036 [JSOI2008]火星人
维护一个字符串序列
1.单点插入
2.查询两个区间的LCP的长度
LCP就是两个字符串的最长公共前缀
Solution
如何判断两个字符串是否相等?
哈希
如何在带插入的情况下维护一个区间的哈希值?
使用平衡树,预处理base的每个次幂的值,这样可以合并两个区间的哈希值
如何查询LCP?
Solution
可以使用二分答案的方法
二分一个区间长度,使用平衡树维护区间哈希的方法来查询这个长度的两个前缀是否相等
时间复杂度O( mlog^2n ),可以优化为O( mlog^2n/loglogn )
其实题目中说了询问次数比较少,询问是O( log^2n )的,插入是O( logn )的
Luogu6327 区间加区间sin和
Solution
考虑这个区间sin和如何维护
大家都记得数学课学过一个东西叫做和差角公式吗
Solution
sin(x+y)=sinxcosy+cosxsiny
cos(x+y)=cosxcosy sinxsiny
所以我们维护区间的sin和,cos和,然后就可以打区间加标记了,这个标记可以合并,也可以下放
BZOJ4373: 算术天才⑨与等差数列
(Luogu3792:由乃与大母神原型和偶像崇拜是这个的弱化版)
给了你一个长度为n的序列
1.询问l,r,k,问区间[l,r]内的数从小到大排序后能否形成公差为k的等差数列。
2.修改一个位置的值
可以先思考一个简单版本:查询的k=1
n<=5e5
Solution1
Luogu3792是BZOJ4373的弱化版,所以这里讲bzoj那个题的做法
首先通过维护区间的min和max就可以知道这个区间是首项为多少,公差为k的等差序列了
直接维护这个信息比较复杂,所以考虑有什么其他的方法可以快速维护
Solution1
首先维护区间的排序后的顺序非常困难
所以考虑维护区间的某些信息,使得这个区间被随机打乱之后维护出来的值是一样的
比如区间1 2 3 4 5和3 4 2 5 1会得到相同的结果
Solution1
首先可以想到区间和,但是比如1 3 5 7和1 4 4 7这两个的和是一样的,但是第一个是公差为2的等差序列,后面的不是
Solution1
那我们同时维护平方和,乘积,立方和之类的不就好了吗
一个给定首项和公差的等差序列的和,平方和是很好计算的
通过维护这些信息就可以极高概率确定这个区间是不是满足条件的了
Solution1
那如果出题人构造数据卡你呢
有个确定性的做法,但感觉还是hash好玩
其实这个题就是一个维护区间hash的思想
Solution2
有没有确定性算法呢?
Solution2
首先我们还是要维护区间的min和max,这样能知道首项和末项
然后考虑一个等差数列的性质:
公差为k的等差数列中任意选出两个元素,他们做差一定是k的倍数。
这样想到,如果把原序列做个差分呢?
Solution2
把一个等差数列重排一下,然后做一个差分,这个差分数组的gcd一定是恰好等于k的,这个是必要条件。
1.如果这个等差数列差分后gcd=a*k,我们发现这个等差数列的公差一定是a*k>k。
2.如果这个等差数列公差是k,差分数组的gcd一定也是k,否则和1一样反证了。
Solution2
考虑把原序列差分,然后维护区间gcd。
还需要什么?还需要区间中不能出现重复的数。
这个我们对每个数维护前驱,然后变成一个数点的问题了。
总时间复杂度O( mlog^2n )
Solution2
其实这个条件比数点弱,是查区间是否每个数的前驱都在区间外,所以维护区间前驱的max就可以了
区间gcd是O( logn + logv )的
总时间复杂度O( m(logn+logv) )
Luogu3586 [POI2015]Logistyka
维护一个长度为n的序列,一开始都是0,支持以下两种操作:
U k a 将序列中第k个数修改为a。
Z c s 在这个序列上,每次选出c个正数,并将它们都减去1,询问能否进行s次操作。
每次询问独立,即每次询问不会对序列进行修改。
1<=n,m<=1000000
1<=k,c<=n,0<=a<=10^9,1<=s<=10^9。
Solution
对于每次询问:
如果ai>=s,则ai可以每s次操作都被选中
如果ai设数列中大于等于s的数有k个,小于s的数的和为sum。
则只需要判断sum>=(c-k)*s即可
Proof
若sum<(c-k)*s
则肯定不能,因为既然和都不够,所以根本不够取
Proof
若sum>=(c-k)*s
由于每个数都小于s,所以有不少于c-k个数
每次从最大的数开始取,一定存在解
Solution
发现需要维护小于x的数的个数,小于x的数的权值和
于是我们用平衡树维护这个序列里面的所有值即可
Luogu6105 [Ynoi2010]iepsmCmq
给定一个常数 C,你需要维护一个集合 S,支持 n 次操作:
1.插入x
2.删除x
每次操作结束后,需要输出从 S 集合中选出两个不同的元素,其的和 mod C 的最大值
n<=5e5,强制在线,不过可以想想离线做法
Solution
我们把每个数对C取模,所以可以认为值域在[0,C)中
发现x+y在[0,2C)中,所以最多减去一个C
对每个x,找出最大的y使得x+y对每个x,找出最大的y(减去一个C)
Solution
发现x+y>=C的情况可以直接找出最大的两个x和y,平凡
只需要考虑x+y如果我们把所有数都排序,假设x如果x1<=x2,则y1>=y2,这个满足单调性
Solution1
问题即,给出一个点集,支持插入删除,和查询max(x+y),使得x+y < C
再继续分析一下,发现如果x,y < C/2,这个也是平凡的
x,y < C/2可以推出 x+y < C,所以选两个最大的C/2以内的数就可以覆盖这部分的贡献
Solution1
目前非平凡的部分在于从[0,C/2)中选一个数x,[C/2,C)中选一个数y,x+y的贡献
x+y我们可以认为最大化x+y是在最小化C-x-y
于是用一棵平衡树维护,这里平衡树这个结构是用来满足x每个在[0,C/2)中的x就直接插入,每个在[C/2,C)中的y,就变成C-y然后插入
平衡树需要维护子树内最小的C-y,最大的x,最小的C-y-x
Solution1
具体一点来说,所有[0,C/2)中的数x看做A集合,所有[C/2,C)中的数y变成C-y后看做B集合
我们要在A和B集合中选出两个数a,b,使得:
a平衡树可以维护这个
Solution1
这个信息显然可以合并
于是我们使用分治结构,做到了O( logn )单次修改
总时间复杂度O( nlogn )
Solution2
还可以发现:
对每个A集合中的x,维护出其在B集合中的后继C-y
对每个B集合中的C-y,维护出其在A集合中的前驱x
这样一定是最优的,
每次修改这个前驱后继变动是O(1)的
这样就可以不用手写平衡树,只需要stl的set就可以了
总时间复杂度O( nlogn )
Luogu6617查找 Search
序列,给定常数w
1.单点修改
2.查询区间是否存在两个数和为w
5e5,4s
Solution
看到问题可以先想到二维数点的转化
每个点x,设置其前驱为离其最近的w-x的位置
这个和区间颜色数的转化类似
如何带修改?
Solution
每次修改可能影响O(n)个位置:
w-x x x x x x x…
这样后面每个位置的前驱都是w-x
如果修改了w-x的值,这样会导致O(n)个修改
观察性质?
Solution
注意到这个是存在性判定
如果存在两个(i1,j1),(i2,j2)使得a[i1]+a[j1]=w,a[i2]+a[j2]=w,而且[i2,j2]包含了[i1,j1],则(i2,j2)没有任何意义
这样每个点只存在O(1)个配对关系
Solution
由于是存在性,所以我们维护b[i]表示每个点的前驱
如果区间[l,r]内b[i]最大值在[l,r]中,则存在,否则不存在
这样只需要rmq线段树,和set维护前驱后继即可
O( n+mlogn )
Luogu5069 [Ynoi2015]纵使日薄西山
珂朵莉想让你维护一个长度为 n 的正整数序列 a[1],…a[n] ,支持修改序列中某个位置的值。
每次修改后问对序列重复进行以下操作,需要进行几次操作才能使序列变为全 0(询问后序列和询问前相同,不会变为全 0):
选出序列中最大值的出现位置,若有多个最大值则选位置标号最小的一个,设位置为 x,则将 a[x],a[x-1],a[x+1] 的值减 1,如果序列中存在小于0的数,则把对应的数改为 0。
Solution
可以发现如果一个位置被操作了,那这个值和旁边两个值会一起减,而且一个位置被操作意味着这个值不会比旁边两个值小
所以这里旁边两个值就不会有贡献了,因为会被中间那个一直操作给提前减到0
Solution
将原序列进行极长单调划分
发现对于每个极长单调区间,答案一定是所有奇数位置或者所有偶数位置的和
Solution
可以发现每次单点修改只会影响到这个点以及左右两个点是否成为局部极大值
还有可能影响到旁边两个极长单调区间的状态
这里影响是O(1)的,所以可以高效维护
细节比较多
O( mlogn )
“李超线段树”
Luogu4069 [SDOI2016]游戏
Luogu4097 [HEOI2013]Segment
区间对一个等差数列取max,查询单点的值,具体题意可以找那个题看看。
Solution
写个线段树
每个节点维护一个永久化的标记,标记存的是一个等差数列,表示这个节点对这个等差数列取了max
Solution
如果这个节点被打上了一个新标记
Solution
我们可以选择把一边的标记下放
Solution
那我们肯定考虑pushdown小的那一段
可以发现每次pushdown的时候标记长度会/2
每次pushdown的复杂度是O( logn ),每个标记会pushdown O( logn )次
所以复杂度为O( mlog^2n )
Solution
查询就是,我们和线段树一样找出和这个位置有关的O( logn )个线段树节点,然后计算这个位置在这些节点上的高度,取个max。
查询复杂度O( logn )
应该可以通过多叉树平衡做到O( mlog^2n/loglogn )
Luogu5608 [Ynoi2013]文化课
n,m<=1e5,3s
Solution
对原序列建一棵线段树,考虑怎么在线段树上面修改和查询
定义 极长 “X” 段为一个极长的子区间,使得区间中符号均为乘法
区间值修改
维护出区间中每个极长的 “X” 段的长度,可以发现这个存在一个自然根号:
假设区间长度为size,则最多只有O( sqrt( size ) )种极长 “X” 段的长度
每次对区间进行值修改的时候,即对这个长度为O( sqrt( size ) )的多项式进行求值,暴力计算即可,求值复杂度为O( sqrt( size ) ),即可以O( sqrt( size ) )的时间将一个节点值进行修改,同时维护信息
区间符号修改
每次对区间符号进行修改的时候,区间的信息只会变成区间和或者区间乘积,所以我们每个节点要维护区间和和区间乘积
符号修改之后,这个节点的极长 “X” 段只会有O( 1 )种了
符号进行修改可能影响一些节点的极长 “X” 段,考虑如何维护这个
区间符号修改
对一个节点,我们可以归并两个儿子的极长 “X” 段,来维护出这个节点的极长 “X” 段
对一个大小为size的节点进行归并,代价是O( sqrt( size ) )的
注意需要特判左儿子的最右极长 “X” 段是否和右儿子的最左极长 “X” 段进行合并
区间信息合并
合并区间信息的时候,只需要把左右儿子信息加起来,同时特判O(1)个位置即可
这O(1)个位置就是左儿子的最右部分和右儿子的最左部分
可以处理:
标记对标记的影响
标记对信息的影响
信息和信息的合并
所以我们正确性有保证了
Complexity
我们所有地方的复杂度都是O( sqrt( size ) )的
线段树在每层只会递归到2=O(1)个节点中,所以每层只有O(1)个节点的信息需要更新
Complexity
T( n ) = T( n / 2 ) + O( sqrtn )
sqrt( n ) + sqrt( n / 2 ) + sqrt( n / 4 ) + … + sqrt( 1 ) = O( sqrtn )
空间:
T( n ) = 2T( n / 2 ) + O( sqrtn )
sqrt( n ) + 2sqrt( n / 2 ) + 4sqrt( n / 4 ) + … + nsqrt( 1 ) = O( n )
总时间复杂度O( msqrtn ),空间复杂度O( n )
由于我不会多项式技术,所以不确定是否存在更优做法,但目前感觉不容易优一个poly(n)
2.简单的均摊复杂度问题
序列染色段数均摊
特点:修改有区间染色操作
用平衡树维护区间的颜色连续段
区间染色每次最多只会增加O( 1 )个连续颜色段,用平衡树维护所有连续段即可
均摊的颜色段插入删除次数O( n + m )
序列染色段数均摊
应用:
区间染色,维护区间的复杂信息
区间排序
“ODT”类问题
注意这里这个颜色段数均摊是有2~3的常数,常数很大
随便YY的题1
给一个序列,每个位置是一个3*3的矩阵
1.区间修改为同一个矩阵
2.查询区间矩阵从左到右的乘积
要求1log
Solution
如果用线段树直接做的话,会发现复杂度是2log的
我们线段树每次push_down的时候,要根据左右两个儿子的size而重新计算矩阵快速幂
如何解决这个问题?
Solution1
我们可以把线段树建成一个2^k长度形式的
然后记录下区间修改矩阵的2^0,2^1…2^k次幂的值
Solution1
每次push_down的时候,儿子的长度也是2^k形式的,这样可以直接利用记录的信息求解
O( n+mlogn )
Solution2
使用序列上的颜色段均摊
每个完整的颜色段我们计算出快速幂
每次查询区间乘积时,发现会完整包含一些颜色段,以及边界上会有O(1)个不完全包含的段
O(1)个不完整的段直接快速幂即可
O( (n+m)logn )
CF453E Little Pony and Lord Tirek
给一个序列
每个位置有初值ai,最大值mi,这个值每秒会增大ri,直到mi
有m个发生时间依此增大的询问,每次询问区间和并且将区间的所有数字变成0
Solution
这个问题每次查询是区间查询并赋值,可以考虑颜色段均摊的方法
假设一段上次修改时间是x,这次修改时间是y,这段的贡献怎么求?
Solution
将贡献分为这段时间充能满了和没满的分别讨论
计算出一个数组a[i]表示i位置从0开始充能充a[i]秒,使得充a[i]+1秒后满
Solution
区间中没充满能的位置即所有i,满足a[i]区间中充满能的位置即上述的补,我们要求这些位置m[i]的和
即变成区间a[i]有初值,颜色段均摊导致查询次数O(n+m)次
总时间复杂度O((n+m)logn)
“重量”平衡树
平衡树旋转/重构的节点的size的和是O( nlogn )
这样可以在旋转的时候暴力重构一些信息
一般用来解决动态标号问题:
序列
1.在x后面插入y
2.查询x和y在序列上的先后问题,这个要求O(1)
可以线性解决,但是由于其他部分一般带log所以OI中一般采用O( nlogn )的解决方法
“重量”平衡树
应用:
套用动态标号法可以得到平衡树维护后缀数组的算法,被称为“后缀平衡树”
可以实现树套树的外层树插入
Luogu5610 [Ynoi2013]大学
序列
1.区间x倍数/x
2.区间和
强制在线
序列长度<=1e5,值域<=5e5
Solution
考虑到一个数最多被除log次,如果除数非1
所以问题变成了如何快速找出x的倍数
Solution
我只会一个很无聊很幼稚很简单很暴力的做法
就是把每个下标插入到其因数的所有平衡树里
然后每次x的倍数/x,就在x对应的平衡树里面暴力查询一段区间的每个数是否是x倍数
由于平衡树的复杂度是O( logn + s )(s是这个区间的点数)
d(v)表示<=v的所有数里面最大的约数个数
所以总复杂度是O( nd(v) + nlognlogv + mlogn )
CF438D
单点修改
区间mod p
区间和
p <= 1e9
Solution
如果x>=2p,x mod p<=p<=2p/2<=x
如果p<=x<2p,x mod p=x-p所以每个数每次会减半,最多logv次之后就变成0了
线段树维护一个区间最大值,能减就减
总复杂度O( (n+m)lognlogv )
HDU 6315 Naive Operations
给两个序列a和b,b是1-n的排列
1.a区间加1
2.求区间内所有[ai/bi]的和
Solution
假设进行了n次全局加
发现全局的和是sigma( n/1 + n/2 + … + n/n ) = O( nlogn )
这是一个调和级数
用树状数组维护答案序列
于是每次如果有一个点的答案发生变化,就在一个点位置+1即可
总复杂度O( mlog^2n )
Solution
怎么找出每次修改的位置呢
线段树维护序列,每个位置初始是 -bi
每次区间加1相当于线段树的区间加1
每次操作完之后,找哪些位置是0,这个可以维护一个最大值来维护出来
把这些0位置直接进行修改即可
UOJ228. 基础数据结构练习题
Solution
sqrt这个操作肯定是一个均摊,因为下降很快
但是有区间加,怎么办呢
想一想感觉可以维护值相同的连续段试试?
Solution
然后就TLE了
发现会被奇怪的数据卡
比如3 4 3 4 3 4
开sqrt后变成1 2 1 2 1 2
然后加2又变成3 4 3 4 3 4
Oh no!
Solution
发现这种情况仅当a=b-1且b是完全平方数的时候会出现
于是想办法维护一下区间极差就可以判掉这种情况
由于取sqrt的次数是O( loglogv )的
所以总复杂度是O( (n+m)lognloglogv )
大概是使用所有连续段以外相邻位置的差来作为势能的均摊
Luogu5068 [Ynoi2015]我回来了& [Code+#7]教科书般的亵渎
珂朵莉在玩炉石传说的时候总是打不出教科书般的亵渎,于是他重新写了一个炉石传说’,并且将亵渎的描述改为:“等概率随机在 [L,R] 中选出一个整数作为伤害值 d,对所有随从造成 d 点伤害,如果有随从死亡,则再次施放该法术,但伤害值不重新随机;如果没有随从死亡,则停止释放”,还去掉了场面上随从上限和亵渎最多触发14次的限制。
珂朵莉不知道这个改版亵渎的效果怎么样,于是他打算进行一些测试,其中共进行 m 次如下类型的操作:
在场面上加入一个血量为 h 的随从,这里随从的血量都不能超过 n;
给定 L, R,询问亵渎期望触发多少次;
珂朵莉只会做操作1,于是他就把操作2交给你啦。
保证: n<=1e5,h<=n,m<=1e6;
Solution
我们考虑亵渎什么时候可以被触发
首先他一定会触发一次,那么这个时候需要让场上所有人的血量-d,想要触发下一次,一定需要有一个人的血量在[1,d]的范围内,如果触发第三次呢?不难发现就是需要有一个人的血量在[d+1,2d]的范围内,以此类推
所以对于伤害值为d的情况,亵渎能够被触发的次数就是最大的k,使得对任意i在[1,k),存在 hj∈[i*(d-1)+1,i*d)
因为每次只有插入一个数,所以我们发现对每个d,k一定会逐渐变大
Solution
变化量是多少呢?
可以发现这个实际上是n/1+n/2+…+n/n=O( nlogn ),是一个调和级数
我们用平衡树维护每个d当前延伸到的位置,每次插入x的时候即在平衡树上暴力找出有哪些d需要继续向后延伸,然后一直延伸
每次一个d改变了延伸到的位置后需要一个树状数组进行单点修改
总时间复杂度O( nlog^2n + mlogn )
[Ynoi2014]誰も彼もが、正義の名のもとに
Solution
考虑用平衡树维护序列,将一段连续的同色极长段缩为一个点
发现操作具有对称性,本质上只有
区间染色为0/1
区间每个数or/and上左/右
区间和
这三种操作
Solution
发现第二种操作其实就是让区间中0/1的同色极长段各自向左/右扩散一格的位置
我们修改的时候不修改这个给定的区间,而是让区间两端点根据操作种类和所在的同色极长段的颜色进行调整,具体来说就是检查一下是否包含这个同色极长段,然后调节我们这次修改的区间的位置
然后问题便转化为,每次区间中0/1的同色极长段各自变大1或者缩小1,这个可以通过在缩点平衡树结构上打标记来实现
Solution
因为有可能一个同色极长段在缩了之后变成0,所以我们需要维护一下区间内最小的同色极长段长度,如果是0则暴力将其删去,同时合并两边的段
可以发现每次修改只会增加O(1)个同色极长段,每次删除可以花O(logn) 的代价减少一个同色极长段
总时间复杂度O((n+m)logn) ,空间复杂度O(n)
Luogu3747 [六省联考2017]相逢是问候
Solution
由欧拉定理,每个数最多变换O( logv )次
因为这里指数每次变为phi(p)
当p为偶数时,phi(p)至少/2
当p为奇数时,phi(p)为偶数
如果phi(p)=1,则继续下去值不变
Solution
于是暴力即可
需要维护区间中每个数是否下次还能进行题目中的操作
每个数可以操作O( logv )次,每次操作需要O( logv )的快速幂,这里均摊的代价是O( log^2v )
总复杂度O( (n+m)(logn+logv)logv )
Old Driver Tree
在有类区间染色操作,以及保证数据随机的情况下
可以用一个平衡树维护颜色连续段的暴力来解决
复杂度期望O( (n+m)loglogn ),可以做到O( n + m ),但是not practical
Old Driver Tree
在线可以做到
O( (n+m)loglogn )(直接做),O( (n+m)logloglogn )(使用exponential tree),
O( n + m )(使用O( logn/logw )的动态前驱数据结构)
离线可以简单的做到O( n + m ),压位即可
Old Driver Tree
可以证明复杂度是期望O( (n+m)logn )的
假设有k种操作,其中一种是区间染色,定义势能为颜色段个数
每次操作的时候有两种可能性:
1.以O( x )的代价消除O( x )势能,势能+2,概率1/k
2.以O( x )的代价啥都没做,势能+2,概率1-1/k
势能的均摊是O( n + m )
于是这部分总的代价是O( (n+m)k )
所以复杂度瓶颈在于平衡树而不是暴力的均摊部分…
Old Driver Tree
应用:
各种题都能用,基本上不会被卡
因为大部分出题人都觉得序列维护的那种数据结构题只需要随机数据就足够强了…
不过要注意,别被没有区间染色的部分分给卡了…
可以水掉各种题
Effect
CF1446D2
给一个序列
求最长的子段使得其中有至少两个出现次数最多的元素。
输出最长子段长度。
Solution
可以证明,这两个出现次数最多的元素中,必定有一个是全局的众数
Solution
假设众数x出现次数为a,我们目前考虑一个值y,计算y与x的答案最大是多少,y出现b次
我们如果得到一个O(a+b)的算法,这个题就是根号题了
我们要得到一个O(b*polylog(n))的算法
Solution
初始将每个x出现的位置标记为无意义的位置
我们枚举y出现的每个位置,然后找离这些位置最近的x出现的无意义位置(左右两边都找),然后将这些位置标记为有意义的位置
Solution
可以证明标记结束后无意义的位置和答案无关
一个位置A无意义,即对其前面所有y出现的位置B,[B,A]之间一定x出现次数>y,同理对后面也成立,所以这个位置不可能是答案端点
所以只有O(b)个可能的答案端点,这里用线段树维护就是O(blogn)的
Solution
由于所有数的出现次数和为n
所以得到一个O(nlogn)的算法
CF765F Souvenirs
区间查两个数的差的最小绝对值
Solution
考虑i位置和哪些位置j能形成有意义的二元组
有意义的二元组即对答案有影响的(i,j)
如果是aiSolution
考虑aiak
1.ai>ak
则|aj-ak|>|ai-ak|,这里有|ai-ak|<1/2|ai-aj|,出现了值域减半
2.ai则|ai-aj|>|ai-ak|,这里限制了一个下界,之后再出现ai总的有贡献的二元组为O(nlogv)个
扫描线+线段树,总时间复杂度O(nlognlogv+mlogn)
Thanks for listening
简单数据结构
信息学奥林匹克竞赛知识点(难点)讲解——数据结构【尖端】
1.序列维护(线段树&平衡树)
线段树
相信大家都会线段树了,所以就不讲原理了
平衡树
全称“平衡二叉搜索树”,常见的类型有:
1.splay
2.treap
3.AVL Tree
4.Red Black Tree
5.Scape Goat Tree
6.Weight Balanced Leafy Tree(特殊结构)
二叉搜索树
性质:一个节点x左子树所有点的关键字都比x的关键字小,右子树所有点的关键字都比x的关键字大
平衡树
限于篇幅,这里只讲一下treap和splay
treap
“树堆”“Tree + Heap”
性质:每个点随机分配一个权值,使treap同时满足堆性质和二叉搜索树性质
复杂度:期望O( logn )
treap
设每个节点的关键字是key,随机权值是rand
1.如果v是u的左儿子,则key[v] < key[u]
2.如果v是u的右儿子,则key[v] > key[u]
3.如果v是u的子节点,则rand[u] > rand[v]
treap
Treap维护权值的时候一般会把相同的权值放在同一个节点上
所以一个treap节点需要维护以下信息:
左右儿子
关键字
关键字出现次数
堆随机值
节点大小(即子树大小)
说要讲模板,这里就利用一下hzwer的吧
旋转
平衡二叉搜索树主要通过旋转来保持树的平衡,即保证复杂度
Treap的旋转
旋转有单旋和双旋,treap只需要单旋,这一点比较简单
Treap的插入
先给这个节点分配一个随机的堆权值
然后把这个节点按照bst的规则插入到一个叶子上:
从根节点开始,逐个判断当前节点的值与插入值的大小关系。如果插入值小于当前节点值,则递归至左儿子;大于则递归至右儿子;
然后通过旋转来调整,使得treap满足堆性质
Code
Treap的删除
和普通的BST删除一样:
如果删除值小于当前节点值,则递归至左儿子;大于则递归至右儿子
若当前节点数值的出现次数大于 1 ,则减一(通常将同一个权值缩掉)
Treap的删除
若当前节点数值的出现次数等于 1 :
若当前节点没有左儿子与右儿子,则直接删除该节点(置 0);
若当前节点没有左儿子或右儿子,则将左儿子或右儿子替代该节点;
若当前节点有左儿子与右儿子,则不断旋转当前节点,并走到当前节点新的对应位置,直到没有左儿子或右儿子为止。
Code
Treap的查询
递归到叶子节点,一路维护信息即可
Treap维护权值
现在大家都会用treap来维护一个集合
支持插入,删除,查询(kth,rank等)了吧
Treap的其他功能
Treap还可以支持维护序列时的分裂合并
这里不详细讲了(我也不会)
具体可以看luogu日报?
splay
“伸展树”“自适应查找树”
splay
每次对一个节点进行操作的时候通过一种方法把这个点旋转至根
需要根据不同的情况判断应该怎么旋转,这里就不详细介绍了
splay
Splay具有“自适应性”
大概就是说splay会根据操作的特点调整树结构,使得操作尽可能高效
可以去了解了解splay的动态最优性猜想,是个著名的open problem
Disadvantage
可以通过势能分析证明splay的复杂度是均摊O( logn )的,也就是说splay在很多次操作中可能会有一次O( n )复杂度的操作
而且这样的操作也很好构造
所以splay不适合做一些需要撤销操作/可持久化的题目(虽然可以通过随机旋转什么的方法来规避,但还是感觉很吃力)
自身常数比较大
Advantage
Splay用来维护序列还是比较好写的,用来维护名次树感觉不好写
由于自适应性,splay不需要特殊的技巧就可以高效启发式合并,还可以高效实现LCT(STT)等动态树
打个广告——WBLT
全称:Weight Balanced Leafy Tree
这个Weight Balanced是指的Balanced by Boundary,也就是BB[α]
和clj那个定义不一样
大概可以理解为通过旋转而不是重构来满足替罪羊树那个平衡关系
也就是说替罪羊树是Weight Balanced Tree的一种
打个广告——WBLT
线段树就是一种Leafy Tree,也就是说把信息都存在叶子上,非叶节点都是存储了信息的合并的虚点(大家可以感性理解一下大概是什么样的一个结构)
优点:目前最好写的平衡树,可持久化效率很高
缺点:非可持久化的情况下要两倍空间,拿来写LCT(STT)很吃力
替罪羊树
定义常数平衡因子α
如果一个点的某个儿子,占到了子树大小的α,则认为不平衡,重构这个子树
复杂度也是带均摊的,均摊O(logn),最坏单次操作O(n)
复杂度证明平凡
大概拿来解决什么样的题
给你一个序列,每次查询区间的******
给你一个树,每次查询链******
Key
是维护的可快速合并的信息,具体怎么定义快速合并比较复杂,这里不进行严谨介绍,只感性理解
Fact
其实这些题就改改线段树的merge函数之类的,相当无聊
Luogu2023 [AHOI2009]维护序列
1.区间加x
2.区间乘x
3.区间和
取膜
Problem
如果只是区间加或者区间乘,直接打个标记就可以了
但是同时有两个操作怎么办
Solution
当然是打两个标记啦,不过需要注意一下处理顺序
维护两个标记,分别是加标记和乘标记
分别设为add和mul
如果一个节点的被加上了x
则add+=x
如果一个节点被乘上了x
则add*=x,mul*=x
注意取膜
即对于标记按顺序维护
先加后乘
常见的打标记的操作
区间加
区间乘
区间染色(区间修改为一个数)
区间翻转
区间xor
Luogu4513 小白逛公园
序列,单点修改,询问区间最大子段和
Solution
著名的新手杀手题。。。
很经典来着
对于每个区间,维护一个左边的最大前缀,右边的最大后缀,以及区间内部的答案
每次合并的时候,即答案选取左子区间的max,右子区间的max,或者左子区间的最大后缀,右子区间的最大前缀即可
很简单的题
Solution
Luogu2042 [NOI2005]维护数列
请写一个程序,要求维护一个数列,支持以下 6 种操作:(请注意,格式栏 中的下划线‘ _ ’表示实际输入文件中的空格)
Solution
pushdown就维护一下区间赋值和区间翻转的标记
update就维护一下区间的最大前后缀和区间的最大子段和,然后更新就可以了
Luogu5482 [JLOI2011]不等式组
你需要维护一堆不等式
1.插入一个ax+b>c的不等式
2.删除第i个插入的
3.查询x=k的时候成立的不等式个数
Solution
如果a>0:ax+b>c x > ( c – b ) / a
如果a<0:ax+b>c x < ( c – b ) / a
如果a=0:是否成立是确定性的
开个平衡树维护值(按值域开个树状数组也行)
然后每次插入取个整
查询直接查rank即可
注意细节
Luogu1471 方差
神犇HansBug在一本数学书里面发现了一个神奇的数列,包含N个实数。他想算算这个数列的平均数和方差。
操作1:1 x y k ,表示将第x到第y项每项加上k,k为一实数。
操作2:2 x y ,表示求出第x到第y项这一子数列的平均数。
操作3:3 x y ,表示求出第x到第y项这一子数列的方差。
Solution
可以通过维护区间和来维护区间平均数
其实就是区间和/区间长度
但是方差呢?
Solution
这里直接粘一个题解里面的公式了
方差可以通过维护平方和和和的平方来算出来
很多这种题直接推推式子就可以维护了
比如SDOI那个无聊的东西
某经典问题
Solution
假设x节点的儿子为y和z
x相邻两数乘积的和为:
y相邻两数乘积的和+z相邻两数乘积的和+y最右边的数*z最左边的数
Solution
假设x节点的儿子为y和z
x任意两数乘积的和为:
y任意两数乘积的和+ z任意两数乘积的和+y的和*z的和
然后直接维护即可。。。
Luogu4198 楼房重建
有一排楼,每次把一个位置的楼的高度修改为x,每次输出可以从最左边看到的楼个数
Solution1
发现一个楼房能被看到可以等价于它的斜率比之前的任何一个都大
所以说我们这里可以直接维护斜率,而不用管楼的高度
问题转化为:
1.单点修改
2.查询全局有多少位置是前缀最大值
Solution1
可以试试分块维护
复杂度好像是O( nsqrt( nlogn ) )的
这里不仔细讲了
Solution2
考虑用线段树维护
对于线段树每个结点维护两个值:ans和max,ans表示只考虑这个区间内的可以被看到的楼房,max表示这个区间的最大楼房斜率。
如何合并区间?
Solution2
合并左右区间的时候:
显然左区间的答案不会变化
问题就是考虑右区间有多少个楼房在左区间的约束条件下仍然可以被看到
Solution2
如果右区间最大值都小于等于左区间最大值,那么右区间就没有贡献了,相当于是被整个挡住了。
Solution2
如果右区间最大值大于左区间最大值
考虑右区间的两个子区间:左子区间、右子区间
Solution2
如果左子区间的最大值小于等于左区间最大值
那么就递归处理右子区间
因为相当于左子区间里面所有楼房都被前面的楼房挡住了了,递归查询右边有多少楼房没被挡住
否则就递归处理左子区间,然后加上右子区间原本的答案,因为这个约束条件弱于左子区间对右子区间的约束,所以只考虑这个约束条件对左子区间的影响~
Solution2
由于要合并O( logn )次,每次合并会递归O( logn )个节点
所以总复杂度O( mlog^2n )
实际上常数非常小
Luogu4036 [JSOI2008]火星人
维护一个字符串序列
1.单点插入
2.查询两个区间的LCP的长度
LCP就是两个字符串的最长公共前缀
Solution
如何判断两个字符串是否相等?
哈希
如何在带插入的情况下维护一个区间的哈希值?
使用平衡树,预处理base的每个次幂的值,这样可以合并两个区间的哈希值
如何查询LCP?
Solution
可以使用二分答案的方法
二分一个区间长度,使用平衡树维护区间哈希的方法来查询这个长度的两个前缀是否相等
时间复杂度O( mlog^2n ),可以优化为O( mlog^2n/loglogn )
其实题目中说了询问次数比较少,询问是O( log^2n )的,插入是O( logn )的
Luogu6327 区间加区间sin和
Solution
考虑这个区间sin和如何维护
大家都记得数学课学过一个东西叫做和差角公式吗
Solution
sin(x+y)=sinxcosy+cosxsiny
cos(x+y)=cosxcosy sinxsiny
所以我们维护区间的sin和,cos和,然后就可以打区间加标记了,这个标记可以合并,也可以下放
BZOJ4373: 算术天才⑨与等差数列
(Luogu3792:由乃与大母神原型和偶像崇拜是这个的弱化版)
给了你一个长度为n的序列
1.询问l,r,k,问区间[l,r]内的数从小到大排序后能否形成公差为k的等差数列。
2.修改一个位置的值
可以先思考一个简单版本:查询的k=1
n<=5e5
Solution1
Luogu3792是BZOJ4373的弱化版,所以这里讲bzoj那个题的做法
首先通过维护区间的min和max就可以知道这个区间是首项为多少,公差为k的等差序列了
直接维护这个信息比较复杂,所以考虑有什么其他的方法可以快速维护
Solution1
首先维护区间的排序后的顺序非常困难
所以考虑维护区间的某些信息,使得这个区间被随机打乱之后维护出来的值是一样的
比如区间1 2 3 4 5和3 4 2 5 1会得到相同的结果
Solution1
首先可以想到区间和,但是比如1 3 5 7和1 4 4 7这两个的和是一样的,但是第一个是公差为2的等差序列,后面的不是
Solution1
那我们同时维护平方和,乘积,立方和之类的不就好了吗
一个给定首项和公差的等差序列的和,平方和是很好计算的
通过维护这些信息就可以极高概率确定这个区间是不是满足条件的了
Solution1
那如果出题人构造数据卡你呢
有个确定性的做法,但感觉还是hash好玩
其实这个题就是一个维护区间hash的思想
Solution2
有没有确定性算法呢?
Solution2
首先我们还是要维护区间的min和max,这样能知道首项和末项
然后考虑一个等差数列的性质:
公差为k的等差数列中任意选出两个元素,他们做差一定是k的倍数。
这样想到,如果把原序列做个差分呢?
Solution2
把一个等差数列重排一下,然后做一个差分,这个差分数组的gcd一定是恰好等于k的,这个是必要条件。
1.如果这个等差数列差分后gcd=a*k,我们发现这个等差数列的公差一定是a*k>k。
2.如果这个等差数列公差是k,差分数组的gcd一定也是k,否则和1一样反证了。
Solution2
考虑把原序列差分,然后维护区间gcd。
还需要什么?还需要区间中不能出现重复的数。
这个我们对每个数维护前驱,然后变成一个数点的问题了。
总时间复杂度O( mlog^2n )
Solution2
其实这个条件比数点弱,是查区间是否每个数的前驱都在区间外,所以维护区间前驱的max就可以了
区间gcd是O( logn + logv )的
总时间复杂度O( m(logn+logv) )
Luogu3586 [POI2015]Logistyka
维护一个长度为n的序列,一开始都是0,支持以下两种操作:
U k a 将序列中第k个数修改为a。
Z c s 在这个序列上,每次选出c个正数,并将它们都减去1,询问能否进行s次操作。
每次询问独立,即每次询问不会对序列进行修改。
1<=n,m<=1000000
1<=k,c<=n,0<=a<=10^9,1<=s<=10^9。
Solution
对于每次询问:
如果ai>=s,则ai可以每s次操作都被选中
如果ai
则只需要判断sum>=(c-k)*s即可
Proof
若sum<(c-k)*s
则肯定不能,因为既然和都不够,所以根本不够取
Proof
若sum>=(c-k)*s
由于每个数都小于s,所以有不少于c-k个数
每次从最大的数开始取,一定存在解
Solution
发现需要维护小于x的数的个数,小于x的数的权值和
于是我们用平衡树维护这个序列里面的所有值即可
Luogu6105 [Ynoi2010]iepsmCmq
给定一个常数 C,你需要维护一个集合 S,支持 n 次操作:
1.插入x
2.删除x
每次操作结束后,需要输出从 S 集合中选出两个不同的元素,其的和 mod C 的最大值
n<=5e5,强制在线,不过可以想想离线做法
Solution
我们把每个数对C取模,所以可以认为值域在[0,C)中
发现x+y在[0,2C)中,所以最多减去一个C
对每个x,找出最大的y使得x+y
Solution
发现x+y>=C的情况可以直接找出最大的两个x和y,平凡
只需要考虑x+y
Solution1
问题即,给出一个点集,支持插入删除,和查询max(x+y),使得x+y < C
再继续分析一下,发现如果x,y < C/2,这个也是平凡的
x,y < C/2可以推出 x+y < C,所以选两个最大的C/2以内的数就可以覆盖这部分的贡献
Solution1
目前非平凡的部分在于从[0,C/2)中选一个数x,[C/2,C)中选一个数y,x+y的贡献
x+y
于是用一棵平衡树维护,这里平衡树这个结构是用来满足x
平衡树需要维护子树内最小的C-y,最大的x,最小的C-y-x
Solution1
具体一点来说,所有[0,C/2)中的数x看做A集合,所有[C/2,C)中的数y变成C-y后看做B集合
我们要在A和B集合中选出两个数a,b,使得:
a
Solution1
这个信息显然可以合并
于是我们使用分治结构,做到了O( logn )单次修改
总时间复杂度O( nlogn )
Solution2
还可以发现:
对每个A集合中的x,维护出其在B集合中的后继C-y
对每个B集合中的C-y,维护出其在A集合中的前驱x
这样一定是最优的,
每次修改这个前驱后继变动是O(1)的
这样就可以不用手写平衡树,只需要stl的set就可以了
总时间复杂度O( nlogn )
Luogu6617查找 Search
序列,给定常数w
1.单点修改
2.查询区间是否存在两个数和为w
5e5,4s
Solution
看到问题可以先想到二维数点的转化
每个点x,设置其前驱为离其最近的w-x的位置
这个和区间颜色数的转化类似
如何带修改?
Solution
每次修改可能影响O(n)个位置:
w-x x x x x x x…
这样后面每个位置的前驱都是w-x
如果修改了w-x的值,这样会导致O(n)个修改
观察性质?
Solution
注意到这个是存在性判定
如果存在两个(i1,j1),(i2,j2)使得a[i1]+a[j1]=w,a[i2]+a[j2]=w,而且[i2,j2]包含了[i1,j1],则(i2,j2)没有任何意义
这样每个点只存在O(1)个配对关系
Solution
由于是存在性,所以我们维护b[i]表示每个点的前驱
如果区间[l,r]内b[i]最大值在[l,r]中,则存在,否则不存在
这样只需要rmq线段树,和set维护前驱后继即可
O( n+mlogn )
Luogu5069 [Ynoi2015]纵使日薄西山
珂朵莉想让你维护一个长度为 n 的正整数序列 a[1],…a[n] ,支持修改序列中某个位置的值。
每次修改后问对序列重复进行以下操作,需要进行几次操作才能使序列变为全 0(询问后序列和询问前相同,不会变为全 0):
选出序列中最大值的出现位置,若有多个最大值则选位置标号最小的一个,设位置为 x,则将 a[x],a[x-1],a[x+1] 的值减 1,如果序列中存在小于0的数,则把对应的数改为 0。
Solution
可以发现如果一个位置被操作了,那这个值和旁边两个值会一起减,而且一个位置被操作意味着这个值不会比旁边两个值小
所以这里旁边两个值就不会有贡献了,因为会被中间那个一直操作给提前减到0
Solution
将原序列进行极长单调划分
发现对于每个极长单调区间,答案一定是所有奇数位置或者所有偶数位置的和
Solution
可以发现每次单点修改只会影响到这个点以及左右两个点是否成为局部极大值
还有可能影响到旁边两个极长单调区间的状态
这里影响是O(1)的,所以可以高效维护
细节比较多
O( mlogn )
“李超线段树”
Luogu4069 [SDOI2016]游戏
Luogu4097 [HEOI2013]Segment
区间对一个等差数列取max,查询单点的值,具体题意可以找那个题看看。
Solution
写个线段树
每个节点维护一个永久化的标记,标记存的是一个等差数列,表示这个节点对这个等差数列取了max
Solution
如果这个节点被打上了一个新标记
Solution
我们可以选择把一边的标记下放
Solution
那我们肯定考虑pushdown小的那一段
可以发现每次pushdown的时候标记长度会/2
每次pushdown的复杂度是O( logn ),每个标记会pushdown O( logn )次
所以复杂度为O( mlog^2n )
Solution
查询就是,我们和线段树一样找出和这个位置有关的O( logn )个线段树节点,然后计算这个位置在这些节点上的高度,取个max。
查询复杂度O( logn )
应该可以通过多叉树平衡做到O( mlog^2n/loglogn )
Luogu5608 [Ynoi2013]文化课
n,m<=1e5,3s
Solution
对原序列建一棵线段树,考虑怎么在线段树上面修改和查询
定义 极长 “X” 段为一个极长的子区间,使得区间中符号均为乘法
区间值修改
维护出区间中每个极长的 “X” 段的长度,可以发现这个存在一个自然根号:
假设区间长度为size,则最多只有O( sqrt( size ) )种极长 “X” 段的长度
每次对区间进行值修改的时候,即对这个长度为O( sqrt( size ) )的多项式进行求值,暴力计算即可,求值复杂度为O( sqrt( size ) ),即可以O( sqrt( size ) )的时间将一个节点值进行修改,同时维护信息
区间符号修改
每次对区间符号进行修改的时候,区间的信息只会变成区间和或者区间乘积,所以我们每个节点要维护区间和和区间乘积
符号修改之后,这个节点的极长 “X” 段只会有O( 1 )种了
符号进行修改可能影响一些节点的极长 “X” 段,考虑如何维护这个
区间符号修改
对一个节点,我们可以归并两个儿子的极长 “X” 段,来维护出这个节点的极长 “X” 段
对一个大小为size的节点进行归并,代价是O( sqrt( size ) )的
注意需要特判左儿子的最右极长 “X” 段是否和右儿子的最左极长 “X” 段进行合并
区间信息合并
合并区间信息的时候,只需要把左右儿子信息加起来,同时特判O(1)个位置即可
这O(1)个位置就是左儿子的最右部分和右儿子的最左部分
可以处理:
标记对标记的影响
标记对信息的影响
信息和信息的合并
所以我们正确性有保证了
Complexity
我们所有地方的复杂度都是O( sqrt( size ) )的
线段树在每层只会递归到2=O(1)个节点中,所以每层只有O(1)个节点的信息需要更新
Complexity
T( n ) = T( n / 2 ) + O( sqrtn )
sqrt( n ) + sqrt( n / 2 ) + sqrt( n / 4 ) + … + sqrt( 1 ) = O( sqrtn )
空间:
T( n ) = 2T( n / 2 ) + O( sqrtn )
sqrt( n ) + 2sqrt( n / 2 ) + 4sqrt( n / 4 ) + … + nsqrt( 1 ) = O( n )
总时间复杂度O( msqrtn ),空间复杂度O( n )
由于我不会多项式技术,所以不确定是否存在更优做法,但目前感觉不容易优一个poly(n)
2.简单的均摊复杂度问题
序列染色段数均摊
特点:修改有区间染色操作
用平衡树维护区间的颜色连续段
区间染色每次最多只会增加O( 1 )个连续颜色段,用平衡树维护所有连续段即可
均摊的颜色段插入删除次数O( n + m )
序列染色段数均摊
应用:
区间染色,维护区间的复杂信息
区间排序
“ODT”类问题
注意这里这个颜色段数均摊是有2~3的常数,常数很大
随便YY的题1
给一个序列,每个位置是一个3*3的矩阵
1.区间修改为同一个矩阵
2.查询区间矩阵从左到右的乘积
要求1log
Solution
如果用线段树直接做的话,会发现复杂度是2log的
我们线段树每次push_down的时候,要根据左右两个儿子的size而重新计算矩阵快速幂
如何解决这个问题?
Solution1
我们可以把线段树建成一个2^k长度形式的
然后记录下区间修改矩阵的2^0,2^1…2^k次幂的值
Solution1
每次push_down的时候,儿子的长度也是2^k形式的,这样可以直接利用记录的信息求解
O( n+mlogn )
Solution2
使用序列上的颜色段均摊
每个完整的颜色段我们计算出快速幂
每次查询区间乘积时,发现会完整包含一些颜色段,以及边界上会有O(1)个不完全包含的段
O(1)个不完整的段直接快速幂即可
O( (n+m)logn )
CF453E Little Pony and Lord Tirek
给一个序列
每个位置有初值ai,最大值mi,这个值每秒会增大ri,直到mi
有m个发生时间依此增大的询问,每次询问区间和并且将区间的所有数字变成0
Solution
这个问题每次查询是区间查询并赋值,可以考虑颜色段均摊的方法
假设一段上次修改时间是x,这次修改时间是y,这段的贡献怎么求?
Solution
将贡献分为这段时间充能满了和没满的分别讨论
计算出一个数组a[i]表示i位置从0开始充能充a[i]秒,使得充a[i]+1秒后满
Solution
区间中没充满能的位置即所有i,满足a[i]
即变成区间a[i]
总时间复杂度O((n+m)logn)
“重量”平衡树
平衡树旋转/重构的节点的size的和是O( nlogn )
这样可以在旋转的时候暴力重构一些信息
一般用来解决动态标号问题:
序列
1.在x后面插入y
2.查询x和y在序列上的先后问题,这个要求O(1)
可以线性解决,但是由于其他部分一般带log所以OI中一般采用O( nlogn )的解决方法
“重量”平衡树
应用:
套用动态标号法可以得到平衡树维护后缀数组的算法,被称为“后缀平衡树”
可以实现树套树的外层树插入
Luogu5610 [Ynoi2013]大学
序列
1.区间x倍数/x
2.区间和
强制在线
序列长度<=1e5,值域<=5e5
Solution
考虑到一个数最多被除log次,如果除数非1
所以问题变成了如何快速找出x的倍数
Solution
我只会一个很无聊很幼稚很简单很暴力的做法
就是把每个下标插入到其因数的所有平衡树里
然后每次x的倍数/x,就在x对应的平衡树里面暴力查询一段区间的每个数是否是x倍数
由于平衡树的复杂度是O( logn + s )(s是这个区间的点数)
d(v)表示<=v的所有数里面最大的约数个数
所以总复杂度是O( nd(v) + nlognlogv + mlogn )
CF438D
单点修改
区间mod p
区间和
p <= 1e9
Solution
如果x>=2p,x mod p<=p<=2p/2<=x
如果p<=x<2p,x mod p=x-p
线段树维护一个区间最大值,能减就减
总复杂度O( (n+m)lognlogv )
HDU 6315 Naive Operations
给两个序列a和b,b是1-n的排列
1.a区间加1
2.求区间内所有[ai/bi]的和
Solution
假设进行了n次全局加
发现全局的和是sigma( n/1 + n/2 + … + n/n ) = O( nlogn )
这是一个调和级数
用树状数组维护答案序列
于是每次如果有一个点的答案发生变化,就在一个点位置+1即可
总复杂度O( mlog^2n )
Solution
怎么找出每次修改的位置呢
线段树维护序列,每个位置初始是 -bi
每次区间加1相当于线段树的区间加1
每次操作完之后,找哪些位置是0,这个可以维护一个最大值来维护出来
把这些0位置直接进行修改即可
UOJ228. 基础数据结构练习题
Solution
sqrt这个操作肯定是一个均摊,因为下降很快
但是有区间加,怎么办呢
想一想感觉可以维护值相同的连续段试试?
Solution
然后就TLE了
发现会被奇怪的数据卡
比如3 4 3 4 3 4
开sqrt后变成1 2 1 2 1 2
然后加2又变成3 4 3 4 3 4
Oh no!
Solution
发现这种情况仅当a=b-1且b是完全平方数的时候会出现
于是想办法维护一下区间极差就可以判掉这种情况
由于取sqrt的次数是O( loglogv )的
所以总复杂度是O( (n+m)lognloglogv )
大概是使用所有连续段以外相邻位置的差来作为势能的均摊
Luogu5068 [Ynoi2015]我回来了& [Code+#7]教科书般的亵渎
珂朵莉在玩炉石传说的时候总是打不出教科书般的亵渎,于是他重新写了一个炉石传说’,并且将亵渎的描述改为:“等概率随机在 [L,R] 中选出一个整数作为伤害值 d,对所有随从造成 d 点伤害,如果有随从死亡,则再次施放该法术,但伤害值不重新随机;如果没有随从死亡,则停止释放”,还去掉了场面上随从上限和亵渎最多触发14次的限制。
珂朵莉不知道这个改版亵渎的效果怎么样,于是他打算进行一些测试,其中共进行 m 次如下类型的操作:
在场面上加入一个血量为 h 的随从,这里随从的血量都不能超过 n;
给定 L, R,询问亵渎期望触发多少次;
珂朵莉只会做操作1,于是他就把操作2交给你啦。
保证: n<=1e5,h<=n,m<=1e6;
Solution
我们考虑亵渎什么时候可以被触发
首先他一定会触发一次,那么这个时候需要让场上所有人的血量-d,想要触发下一次,一定需要有一个人的血量在[1,d]的范围内,如果触发第三次呢?不难发现就是需要有一个人的血量在[d+1,2d]的范围内,以此类推
所以对于伤害值为d的情况,亵渎能够被触发的次数就是最大的k,使得对任意i在[1,k),存在 hj∈[i*(d-1)+1,i*d)
因为每次只有插入一个数,所以我们发现对每个d,k一定会逐渐变大
Solution
变化量是多少呢?
可以发现这个实际上是n/1+n/2+…+n/n=O( nlogn ),是一个调和级数
我们用平衡树维护每个d当前延伸到的位置,每次插入x的时候即在平衡树上暴力找出有哪些d需要继续向后延伸,然后一直延伸
每次一个d改变了延伸到的位置后需要一个树状数组进行单点修改
总时间复杂度O( nlog^2n + mlogn )
[Ynoi2014]誰も彼もが、正義の名のもとに
Solution
考虑用平衡树维护序列,将一段连续的同色极长段缩为一个点
发现操作具有对称性,本质上只有
区间染色为0/1
区间每个数or/and上左/右
区间和
这三种操作
Solution
发现第二种操作其实就是让区间中0/1的同色极长段各自向左/右扩散一格的位置
我们修改的时候不修改这个给定的区间,而是让区间两端点根据操作种类和所在的同色极长段的颜色进行调整,具体来说就是检查一下是否包含这个同色极长段,然后调节我们这次修改的区间的位置
然后问题便转化为,每次区间中0/1的同色极长段各自变大1或者缩小1,这个可以通过在缩点平衡树结构上打标记来实现
Solution
因为有可能一个同色极长段在缩了之后变成0,所以我们需要维护一下区间内最小的同色极长段长度,如果是0则暴力将其删去,同时合并两边的段
可以发现每次修改只会增加O(1)个同色极长段,每次删除可以花O(logn) 的代价减少一个同色极长段
总时间复杂度O((n+m)logn) ,空间复杂度O(n)
Luogu3747 [六省联考2017]相逢是问候
Solution
由欧拉定理,每个数最多变换O( logv )次
因为这里指数每次变为phi(p)
当p为偶数时,phi(p)至少/2
当p为奇数时,phi(p)为偶数
如果phi(p)=1,则继续下去值不变
Solution
于是暴力即可
需要维护区间中每个数是否下次还能进行题目中的操作
每个数可以操作O( logv )次,每次操作需要O( logv )的快速幂,这里均摊的代价是O( log^2v )
总复杂度O( (n+m)(logn+logv)logv )
Old Driver Tree
在有类区间染色操作,以及保证数据随机的情况下
可以用一个平衡树维护颜色连续段的暴力来解决
复杂度期望O( (n+m)loglogn ),可以做到O( n + m ),但是not practical
Old Driver Tree
在线可以做到
O( (n+m)loglogn )(直接做),O( (n+m)logloglogn )(使用exponential tree),
O( n + m )(使用O( logn/logw )的动态前驱数据结构)
离线可以简单的做到O( n + m ),压位即可
Old Driver Tree
可以证明复杂度是期望O( (n+m)logn )的
假设有k种操作,其中一种是区间染色,定义势能为颜色段个数
每次操作的时候有两种可能性:
1.以O( x )的代价消除O( x )势能,势能+2,概率1/k
2.以O( x )的代价啥都没做,势能+2,概率1-1/k
势能的均摊是O( n + m )
于是这部分总的代价是O( (n+m)k )
所以复杂度瓶颈在于平衡树而不是暴力的均摊部分…
Old Driver Tree
应用:
各种题都能用,基本上不会被卡
因为大部分出题人都觉得序列维护的那种数据结构题只需要随机数据就足够强了…
不过要注意,别被没有区间染色的部分分给卡了…
可以水掉各种题
Effect
CF1446D2
给一个序列
求最长的子段使得其中有至少两个出现次数最多的元素。
输出最长子段长度。
Solution
可以证明,这两个出现次数最多的元素中,必定有一个是全局的众数
Solution
假设众数x出现次数为a,我们目前考虑一个值y,计算y与x的答案最大是多少,y出现b次
我们如果得到一个O(a+b)的算法,这个题就是根号题了
我们要得到一个O(b*polylog(n))的算法
Solution
初始将每个x出现的位置标记为无意义的位置
我们枚举y出现的每个位置,然后找离这些位置最近的x出现的无意义位置(左右两边都找),然后将这些位置标记为有意义的位置
Solution
可以证明标记结束后无意义的位置和答案无关
一个位置A无意义,即对其前面所有y出现的位置B,[B,A]之间一定x出现次数>y,同理对后面也成立,所以这个位置不可能是答案端点
所以只有O(b)个可能的答案端点,这里用线段树维护就是O(blogn)的
Solution
由于所有数的出现次数和为n
所以得到一个O(nlogn)的算法
CF765F Souvenirs
区间查两个数的差的最小绝对值
Solution
考虑i位置和哪些位置j能形成有意义的二元组
有意义的二元组即对答案有影响的(i,j)
如果是ai
考虑ai
1.ai>ak
则|aj-ak|>|ai-ak|,这里有|ai-ak|<1/2|ai-aj|,出现了值域减半
2.ai
扫描线+线段树,总时间复杂度O(nlognlogv+mlogn)
Thanks for listening
同课章节目录
