根号数据结构课件-2021-2022学年中学生信息学奥林匹克竞赛数据结构(难点)精讲(333张PPT)
文档属性
| 名称 | 根号数据结构课件-2021-2022学年中学生信息学奥林匹克竞赛数据结构(难点)精讲(333张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2021-12-19 11:12:27 | ||
图片预览








文档简介
(共333张PPT)
根号数据结构
信息学奥林匹克竞赛知识点(难点)精讲——数据结构【尖端】
Notice
如果没有专门说明
默认n = 1e5 , m = 1e5
分块基础
分块的分类
静态分块
动态分块
静态分块指的是放一些关键点,预处理关键点到关键点的信息来加速查询的,不能支持修改
目前认为:如果可以离线,静态分块是莫队算法的子集
动态分块指的是把序列分为一些块,每块维护一些信息,可以支持修改
动态分块基础
下列提到的分块默认为动态分块
分块基础
要实现:
1.区间加
2.区间和
朴素来做,可以有O(1)修改O(n)查询以及O(n)修改O(1)查询的暴力做法
这个问题可以套用根号平衡达到O( sqrt(n) )修改O( sqrt(n) )查询
我们可以把sqrt(n)个元素放一块里面维护
分块基础
我们把每次操作完整覆盖的块定义为“整块”
把每次操作没有完整覆盖的块定义为“零散块”
分块基础
每次操作最多经过O( sqrt(n) )个整块,以及2个零散块
所以我们可以O(1)维护整块信息,O( sqrt(n) )查询零散块信息
这样就达到了O( msqrt(n) )的复杂度
分块
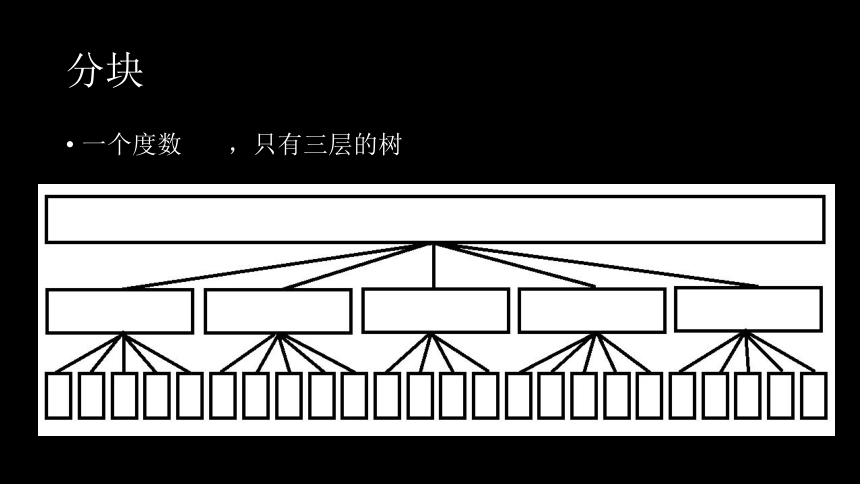
一个度数 ,只有三层的树
分块
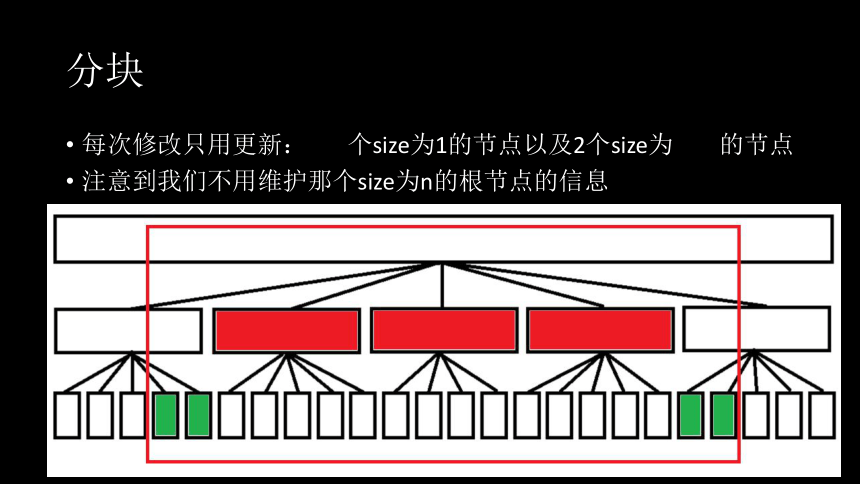
每次修改只用更新: 个size为1的节点以及2个size为 的节点
注意到我们不用维护那个size为n的根节点的信息
分块的作用
所以如果在分治结构上很难快速合并某些信息,我们就可以利用分块来做
经典问题
Solution
如果是单点修改,我们可以用树套树实现
但是区间修改后树套树无法快速合并信息
比如我们维护了cur的一个名次数据结构
cur的左儿子没有发生变化
cur的右儿子被整体加了
这样我们无法通过这两个儿子的名次数据结构快速维护出cur的名次数据结构
也无法直接在cur的名次数据结构上操作
所以分治结构无法在低复杂度解决这个问题
Solution
分块,维护每块的OV(就是排序后的数组)
每次区间加的时候
整块可以打一个标记
零散块可以重构
每次查询的时候
整块查询小于x的数,这个整块的标记为y(也就是说这一块所有数都加了y)
则等价于查整块的排序后的数组里面小于x-y的数的个数
这个可以二分
零散块就直接暴力查询块内在查询区间内的数是否满足条件
Complexity
设有x个块
查询复杂度:
整块O( log(n / x) ) * x
零散块O( n / x )
修改复杂度:
整块O( 1 )
零散块O( n / x ) (重构的时候用归并)
按照根号平衡算一算可以发现
总复杂度O( msqrt( nlogn ) )
此时块大小为sqrt( nlogn )
Solution
大概有另外两个O( msqrt( n ) )的做法
不过没有什么太大的实用价值,写起来很麻烦,常数较大,不一定比O( msqrt( nlogn ) )做法快,也基本上没人会
所以这里就不讲了
[Ynoi2017] 由乃打扑克
Solution
Solution
Solution
Solution
存在O( msqrt( nlogn ) )的算法,基于复杂的多序列二分,not practical
用根号平衡来优化数据结构复杂度
根号平衡
根号平衡
根号平衡
修改:
查询:
根号平衡
根号平衡
分块维护块内前缀和和块外前缀和
也就是说维护每个块块内前x数的和
以及维护前x的块的和
更新的时候分别更新这两个前缀和
查询的时候把这两个前缀和拼起来
根号平衡
修改:
查询:
根号平衡
维护一个序列,支持:
O( sqrt(n) )区间加,O(1)查单点
根号平衡
直接分块
根号平衡
修改:
查询:
根号平衡
根号平衡
根号平衡
修改:
查询:
根号平衡
根号平衡
根号平衡
修改:
查询:
根号平衡
根号平衡
值域分块
对于每个数维护一下其在哪个块里面
对于每个块维护一个OV(有序表)表示这个块内的所有数存在的数,从小到大
这样我们修改的时候只会改变sqrt( n )个数所从属的块
查询的时候定位到其所属于的块,然后找到其在该块中对应的值
根号平衡
修改:
查询:
CodeChef Chef and Churu
给长为n的序列,给定m个函数,每个函数为序列中第li 到第ri个数的和
有q个两种类型的操作:
1 x y 把序列中的第x个数改为y
2 x y 求第x个函数到第y个函数的和
Solution
因为函数不变,所以把函数分块
维护一个前i个块的函数的前缀和,代表前i个块中每个序列上的点的出现次数
然后再维护一个前i个块的函数的答案
每次修改只需要查询这个序列上的点在前i个块的函数中的出现次数即可
然后零散的部分,即用一个O( sqrt(n) )修改,O( 1 )查询的分块维护即可
O( nsqrtn + msqrtn ) = O( msqrtn )
Solution
可能存在polylog做法,但我想了想不会,这里只是通过此题介绍一下分块
Luogu3863 序列
Solution
简单莫队算法
普通莫队算法
理想莫队信息:维护一个子集的信息,支持O( a )插入一个元素,O( b )删除一个元素,无法比直接暴力更高效地合并
问题:给出一个点集,多次询问点集的一个子集的信息
这里只考虑类似区间信息的维护
普通莫队的本质
假设有两个区间询问
[l1,r1],[l2,r2]
如果我们可以O(x)插入或者删除一个元素
即我们已经得到了[l,r]的答案
可以O(x)转移得到
[l,r+1],[l,r-1],[l-1,r],[l+1,r]的答案
那么我们可以O( x * ( |r1-r2|+|l1-l2| ) )
由[l1,r1]的答案得到[l2,r2]的答案
普通莫队的本质
于是序列长n,有m个询问
我们可以以一种特殊的顺序依次处理每个询问
使得sigma( |li-li-1| + |ri-ri-1| )在一个可以接受的范围内
可以对序列分块,然后把询问排序
排序的时候以左端点所在块编号为第一关键字
右端点位置为第二关键字
普通莫队的本质
可以证明这样的复杂度是O( nsqrt( m ) + m )的
普通莫队的本质
普通莫队的本质
有没有更优的做法呢
我们可以用曼哈顿距离最小生成树去近似这个问题
把每个询问[l,r]看做二维平面上的点
于是我们按照建出来的曼哈顿距离最小生成树去DFS
这个做法的复杂度和最优转移一定是同阶的
曼哈顿距离最小生成树和刚刚介绍的排序算法的最坏复杂度是一样的,所以莫队问题可以直接按块排序
普通莫队的优秀写法
普通莫队卡常数的基本方法
排序要按照奇偶分别排
这样可以块一倍
调那个常数可以块10%左右
经典问题
查询一个区间中每个数出现次数的平方和
Solution
裸上莫队,定义cnt[x]为x的出现次数
每次更新的时候,如果插入一个x
则ans += 2 * cnt[x] + 1
如果删除一个x
则ans -= 2 * cnt[x] – 1
Notice
此题存在O( n^1.41 )的算法,依赖快速矩阵乘法而not practical
[Ahoi2013]作业
Solution1
Solution1
Solution1
Solution1
Solution2
显然存在polylog解法,这里不做介绍
[Ynoi2016]这是我自己的发明
Hint
Solution
Solution
Bzoj3920 Yunna的礼物
Technology
Technology
Solution
Bzoj4241历史研究
序列,定义Chtholly(l,r,x)为x在区间[l,r]中出现次数,查询一个区间中最大的x*Chtholly(l,r,x)
Solution
[Ynoi2015]いずれその陽は落ちるとしても
Solution
考虑单次询问怎么算
对于数x,假设出现了y次,区间长度是len
则x对答案的贡献是
是除了x之外的数有这么多个不同的子序列,这些对x的贡献没有影响
是所有x构成的子序列中有 种至少包含一个x,有1种不包含x
Solution
Solution
注意到贡献分为两部分 与
其中第一部分非常好维护
第二部分的贡献,可以把出现次数相同的数一起维护贡献
注意到一个区间中只有O( sqrt( n ) )种不同的出现次数
Solution1
Solution2
Luogu3245 HNOI2016大数
给一个数字串以及一个质数p
多次查询这个数字串的一个子串里有多少个子串是p的倍数
Solution
记suf[i]为i -> n构成的后缀串
如果对于l,r有suf[l] % p == suf[r+1] % p
则s[l...r] * 10 ^ ( n - r - 1 )为p的倍数
Solution
对p=2,5时特判
p!=2,5时s[l...r] * 10 ^ ( n - r - 1 )为p的倍数即意味着s[l...r]为p的倍数
离散化一下,然后就变成小Z的袜子了
Luogu3604 美好的每一天
Solution
Solution
Solution
经典问题
查询区间逆序对个数
吐槽
Brute
Solution
为什么要维护区间树状数组?
Solution1
可以维护一个可持久化块状树
或者称为可持久化值域分块吧
可以理解为把分块的树可持久化一下
Solution1
根号平衡:
可持久化Trie:
O( logn )插入+可持久化
O( logn )查询区间小于x的数个数
可持久化块状树:
O( sqrtn )插入+可持久化
O( 1 )查询区间小于x的数个数
Solution1
But
Question
难道这个logn不可卡吗
Answer
Notice
此题存在O( n^1.41 )的算法,依赖快速矩阵乘法而not practical
莫队二次离线
莫队二次离线
莫队二次离线
具体实现:区间逆序对的Solution2
Problem
Possibility
可不可以优化这个的空间呢?
Optimization
如果可以把空间优化至O( n + m )
则一切问题都解决了
(时间消耗大的最大问题是空间太大导致内存访问代价过高引起的)
Optimization
深入挖掘这个莫队的性质
发现莫队只有O( m )次本质不同的询问:
区间[l1,r1-1]内与a[r1]有关的一个信息
区间[l1,r1-2]内与a[r1-1]有关的一个信息
区间[l1,r1-3]内与a[r1-2]有关的一个信息
......
区间[l1+1,r1]内与a[l1]有关的一个信息
区间[l1+2,r1]内与a[l1+1]有关的一个信息
区间[l1+3,r1]内与a[l1+2]有关的一个信息
......
Optimization
这个明显很有规律
可以针对莫队的4种转移推一下其贡献
发现有6种贡献:
+/-前缀x内序列区间为[l,r]的所有数的贡献
+/-前缀[l,r]内其右边+1位置的数的贡献
+/-前缀[l,r]内其自己的贡献
第一种可以直接在每个地方开个vector,然后push_back一个pair表示区间来实现
后面两种可以通过打差分标记来实现
Optimization
这个存在简洁很多的写法,讲后面的题的时候回提到
树上莫队
查询链信息
查询子树信息
如果是查询子树的理想莫队信息,那么子树信息可以启发式合并上来,是polylog的
树上莫队
查询链的信息
有多种实现方法
第一种是将树的联通块分块,在树上跑莫队
另一种是将树的括号序分块,在括号序上跑莫队
我们也可以使用更好的树分块方法,不过链太弱了所以没有必要
无论代码难度,常数来说都是括号序更优
这里只介绍括号序
括号序
即DFS树的时候
进入x点就push_back( +x )
走出x点就push_back( -x )
莫队转移的时候
如果新加入的值是+x,就加入x
如果新加入的值是-x,就删除x
如果新删除的值是+x,就删除x
如果新删除的值是-x,就加入x
带修改莫队
普通的莫队是在转移二元组状态(l,r)
如果带修改,可以加上一维表示时间
把状态变成三元组状态(l,r,t)
这个新的状态可以在一个可以O(1)转移到
(l,r,t-1) (l,r,t+1)
(l-1,r,t) (l+1,r,t)
(l,r-1,t) (l,r+1,t)
可以用和普通莫队类似的方法排序转移,做到O( n^5/3 )
不删除莫队
莫队转移需要可以在一个可以接受的复杂度达到:
由(l,r)转移到(l-1,r),(l+1,r),(l,r-1),(l,r+1)
然而有的信息不支持快速删除(比如max)
可以通过一些方法使得其只要支持按顺序撤销,而不用支持删除
经典问题
Brute
Possibility
Solution
Solution
Solution
Solution
Solution
整个的区间为[x,y]
蓝色的区间为[l,r]
即我们需要删除绿色的区间里面所有的数
Solution
考虑撒t个关键点
如果维护了关键点到关键点的信息
则我们[x,y]只要找到最近的关键点l满足l<=x,最近的关键点r满足y<=r即可O( n/t )从区间[l,r]转移到区间[x,y]
我们知道所有关键点的位置后
可以离线每个询问,就知道每个询问是由哪一对关键点得来的
Solution
Notice
Notice
Notice
这个题有nlognlogv的线段树做法
可以去cf上翻翻
Bzoj4358 permu
Solution 引用自ccz181078博客
CodeChef QCHEF
序列,每个询问求区间[L,R]中值相同时,位置差的最大值
即最大的|x-y|使得L<=x,y<=R且a[x]==a[y]
Solution
Luogu5386 [Cnoi2019]数字游戏
给定一个排列,多次询问,求一个区间 [l,r] 有多少个子区间的值都在区间 [x,y] 内。
Solution
这个题我们可以考虑用莫队跑值域区间
我们把值在目前莫队跑的区间内的序列位置标为1,否则标为0
发现答案就是在序列的一个区间中,每个极长1的段的size的平方,这样的东西
Solution
我们对序列分块后,每个块维护块内的答案,这样如果我们知道每次修改的极长1段的位置,我们就可以O(1)修改了
上面一题给出了一个不删除莫队维护极长1段的方法,直接套用就行了
总时间复杂度O( nsqrtm + msqrtn )
静态分块基础
下列提到的分块默认为静态分块
分块的本质
经典问题
给一个序列,每次查询一个区间的众数,强制在线
Solution1
之前几个题属于带修改的动态分块,这个题就属于只带查询的静态分块了
如何合并信息?
对于众数有一个性质:
如果x是集合A里面的众数,我们往集合A里面加入集合B里面的所有数
现在新集合的众数只会是x或者集合B里面的数
Solution1
序列上每隔根号个数放一个关键点
预处理每两个关键点之间的众数
这个可以以每个关键点为开头for一下序列实现
Solution1
查询的时候
我们已经预处理了黄色部分的众数了
只需要加入蓝色的点,蓝色的点只有 一个一个验证即可
Solution1
验证的时候需要快速查询一个数在一个区间中出现次数
如果用可持久化Trie来维护,单次查询O( logn )
总复杂度O( msqrt( n )logn )了
Solution1
注意到
我们只需要支持一个可持久化的数据结构
插入n次,查询msqrtn次
这个可以利用根号平衡
也就是说我们需要有一个可持久化的数据结构支持
O( sqrt( n ) )插入,O( 1 )查询
显然可以利用可持久化块状树(可持久化值域分块)实现
Solution1
还有另一个做法
即维护每个值在前i个块中的出现次数
这个数在第x到第y个块中出现次数
即为在前y个块中的出现次数减去前x-1个块中的出现次数
每次先把零散加进去
这样就可以O(1)查询一个数在区间中出现次数了
Solution1
通过用这个
可以做到复杂度
O( nsqrt( m ) )
Technology
这样的区间众数空间是O( nsqrt(n) )的
可以进行一次根号分治做到O( n^1.25 )
还有个论文方法可以做到空间O( n ),而且基本上没常数
Solution2
我们可以对每个值开个vector,记下每个位置在vector中的位置
可以发现,假设我们现在在x位置,我们目前众数出现次数为y,现在在从右往左边扫
那我们只需要check答案是否会增大1就可以了
那么就是vector[ belong(x) + y ]这个位置在不在区间[l,r]内部
这个我们可以O( 1 )找到,所以可以O( 1 )拓展
这样达成了线性空间
Technology
离线存在O( n^1.48541 )的算法,基于对max-plus形式的稀疏矩阵乘法的优化,not practical
经典问题
强制在线,查询区间逆序对
Solution
主要思想还是通过差分和归并来优化复杂度
考虑把序列分成sqrtn块
预处理任意两个关键点之间的信息
Solution
查询答案的时候:
答案为l和r整块内的贡献
加上两个零散块对整块块内贡献
加上零散块之间贡献
红色为整块内贡献
绿色为两个零散块对整块贡献
黄色为零散块间贡献
Solution
设f(l,r)为第l到第r个块之间的逆序对个数
设g(l,r)为第l个块中任选一个数x,第r个块中任选一个数y,
如果x>y则ans++
即第l个块与第r个块可以造成的贡献
差分,可得f(l,r)=f(l+1,r)+f(l,r-1)-f(l+1,r-1)+g(l,r)
g(l,r)即对于l中每个数查询r中大于其的数个数
这个可以归并实现
这部分总复杂度O( sqrt(n) * sqrt(n) * sqrt(n) ) = O( nsqrt(n) )
Solution
Solution
零散块对整块的贡献可以差分
即预处理出零散块对前i个整块的贡献
于是对[l,r]这些整块的贡献即pre[r] - pre[l-1]
考虑到零散块最多只有O( n )种
整块有O( sqrt(n) )个
于是复杂度O( (n+m)sqrt( n ) )
Solution
零散块对零散块的贡献可以归并得到
O( sqrt( n ) )
总复杂度O( nsqrt( n ) + msqrt( n ) )
常数较大
经典问题
强制在线,序列,多次查询一个区间[l,r]内
最小的|ai-aj| , l <= i , j <= r
Solution
还是用刚刚的方法
可以O( nsqrt( n ) )预处理出块内的答案
考虑一个零散块会和哪些块有贡献
必然是从其前面那个块开始的一个后缀
Solution
于是可能的零散块-整块贡献只有nsqrt( n )种
对于每个零散块维护一个后缀min即可
零散块和零散块的贡献还是归并得到
O( (n+m)sqrt( n ) )
多区间合并
给定一个序列,多次查询区间幺半群信息
幺半群可以粗略认为是可以O(1)合并,不能差分的信息
预处理复杂度:O( n * f(n,k) ),查询的时候合并k次,k+1个区间
k=0:f(n,0)=n
k=1:f(n,1)=logn,所谓的“猫树”
k=2:f(n,2)=loglogn,所谓的“sqrt-tree”
k=3,4:f(n,3)=f(n,4)=log*n
…
k=α(n):f(n,α(n))=α(n)
根号分治
根号分治
一个不怎么好的抽象:
有n个数和为m,则最多有m/a个数大于a
剩下的数都不大于a
如果对于每个大于a的数我们可以O(x)维护
那我们就以O( xa )的额外复杂度保证了这些数都<=a
经典问题
给一张n个节点m条边的无向图
n,m,q<=1e5
1.把x点权加y
2.查询x相邻的点权和
Solution
图中每个点的度数和是m
我们可以对这个度数进行根号分治
度数>=sqrt(m)的点最多只有sqrt(m)个
度数Solution
对每个度数>=sqrt(m)的点维护答案
每次修改
枚举所有度数>=sqrt(m)的点,如果和修改点相邻,则更新答案
每次查询
如果这个点度数>=sqrt(m),直接输出维护的答案
如果这个点度数总复杂度O( qsqrt(m) )
经典问题
序列a,每次给个x和y
查询最小的|i-j|
使得ai==x,aj==y
Solution
对于颜色进行根号分治
出现次数大于sqrt(n)的颜色只有sqrt(n)种
预处理这些颜色到每个颜色的答案
这一步是O( sqrt(n) * n ) = O( nsqrt(n) )的
Solution
这样如果查询的x和y
其中有一个是出现次数大的颜色
我们可以O(1)得到答案
如果没有呢?
Solution
如果没有,那最多有各sqrt(n)个位置值为x,y
可以进行归并排序来维护答案
这部分复杂度为O( msqrt(n) )
总复杂度O( nsqrt(n) + msqrt(n) )
IOI2009 Regions
N个节点的树,有R种属性,每个点属于一种属性。
有Q次询问,每次询问r1,r2,回答有多少对(e1,e2)满足e1属性是r1,e2属性是r2,e1是e2的祖先。
Solution
把询问离线一下(为了线性空间)
还是对颜色进行根号分治
推推式子即可
SHOI2006 Homework
1 X : 在集合 S 中加入一个X,保证 X 在当前集合中不存在。
2 Y : 在当前的集合中询问所有X mod Y最小的值
X,Y <= 1e5
Solution
考虑根号分治
对于sqrtn以内的Y,每次修改即更新所有这个的答案
对于sqrtn以上的Y,即需要支持:
O( sqrtn )修改,O( 1 )查询前驱后继
我们对值域分块
每个块中位置维护出
1.块内其前面最近的X
2.如果块内其前面没有X,则维护出其最近的有X的块
Solution
修改的时候,我们修改X所在块内的1
然后枚举每个后缀的块,将其2对这个块取max
同时维护块内最后的一个X
查询时,如果当前查询的kY在块内有1的答案,则使用
否则使用其2的答案的块的最后的一个X
总时间复杂度O(msqrtv)
POI2015 Odwiedziny
树,点权,多次查询,每次给x,y,k
求从x开始,每次跳过k个节点跳到y,所经过节点的和
保证跳到y
Brute
考虑对k根号分治
如果k <= sqrt(n),可以将询问离线,对每个k=1...sqrt(n)都跑一遍
如果k > sqrt(n),最多跳上sqrt(n)次
k <= sqrt(n)时单次可以做到O(n)
k > sqrt(n)时用倍增/树链剖分求k祖先,单次O( logn )
总复杂度O( nsqrt(n) + msqrt(n)logn )
简单根号平衡后达到O( msqrt(nlogn) )
Improved Algorithm
可以用O(1) k祖先的方法来实现
预处理可以写O( nsqrt(n) )的,这样查询常数较小
或者可以用树链剖分,边跑边找出这个重链上所有该算进去的点
O( sqrt(n) + logn )
[Ynoi2015]いまこの時の輝きを
查询一个区间乘积的约数个数
mod 19260817
值域v<=1e9
Brute
一个数的约数个数
即为:
Pi为i出现次数
对于每个数,质因子的个数只有logv个
(我不会打公式)
Brute
可以莫队暴力维护区间的这个东西
每次转移O( logv )
总复杂度O( nsqrt(m)logv )
TLE
Improved Brute
考虑到一个数本质不同的约数个数并没有logv个
最坏的情况是2*3*5*7...这样
其实这个的个数是O( logv/loglogv )
还是莫队转移
O( nsqrt(m)logv/loglogv )
TLE
Solution
可以用根号分治优化复杂度
一个数大于v^1/3的质因数只有2个
小于等于v^1/3的质数只有v^{1/3}/logv个
当v=1e9时,小于1000的质数只有168个
Solution
跑莫队的时候只维护大于v^1/3的质数的贡献
这一部分是O( nsqrt(m) )的
小于等于v^1/3的质数,每个开一个前缀和,就可以O(1)知道其在区间中出现次数
这一部分是O( m v^{1/3} /logv )的
然后对于每个数分解质因数是O( n v^1/4 )的
总复杂度O( n(v^{1/4}) + m(v^{1/3})/logv + nsqrt(m) )
根号重构
根号重构
本质为时间分块
假设:
可以O(x)重构整个序列
可以O(y)算出一个修改操作对一次查询的影响
如果每隔t个修改重构整个序列
则复杂度为O( tx )+O( m^2/ty )
经典问题
带link cut树上路径kth
(基于树分块也可以同复杂度维护,这里讲根号重构的做法)
Solution
根号重构,每过sqrtm次重构一次
这样一次操作会转换为查询sqrtm段上次重构后的树链的kth
用可持久化Trie维护,在这sqrtm个Trie上一起二分
每次查询复杂度O( sqrtmlogn )
每次重构复杂度O( nlogn )
总复杂度O( msqrtmlogn + nsqrtmlogn ) = O( (n+m)sqrtmlogn )
树上分块
Topology cluster partition
真实的树分块——Topology Cluster Partition
树分块将 n 个结点的树分成了一些块的并,满足下列性质:
1.每个块是树
2.每个块中有两个特殊的点,称为端点 1 和端点 2。
3.不同块的边集不相交
4.一个块中的顶点,除端点外,其余顶点不在其它块中出现
5.如果一个顶点在多个块中出现,那么它一定是某一个块的端点 2,同时是其余包含这个顶点的块的端点 1
6.如果把所有块的端点作为点,每块的端点 1 和端点 2 连有向边,则得到一棵有根树
Topology cluster partition
怎么求出来呢?
可以发现这个cluster和top tree的cluster是一样的,所以我们把原树的top tree建出来,然后从中提取O( sqrt( n ) )所对应的那一层即可,时间复杂度O( nlogn )
有没有简单一点的做法?
Topology cluster partition
这里给出树分块的一个实现,满足块数和每块大小均为 O( sqrtn ):
在有根树中,每次选一个顶点 x,它的子树大小超过sqrtn,但每个孩子的子树大小不超过sqrtn, 把 x 的孩子分成尽可能少的块(以 x 为端点 1,但暂时允许有多个端点 2,且每块至多有 2sqrtn 个顶点),然后删掉 x 的子树中除 x 外的部分。
重复直到剩下的点数不超过sqrtn,自成一块。
这样就求出一个保证块中顶点数和块数均为 O( sqrtn )的树分块(块间可以共用一些顶点,但每条边只属于一个块),如果一个块有多个端点(即被多个块共用的点),则在块内将这些端点 建出虚树,将虚树上的每条边细分为一个新的块,以保证最终每个块只有两个端点。
树分块
不过一般我们树分块可以更简单一些,因为一般只需要查链信息
随机撒O( sqrtn )个点,期望复杂度是正确的
COT
Solution
进行树分块,预处理任意两个关键点之间有多少种颜色
每次查询的时候一直往上跑,找到最近的关键点,得到整块的答案
Solution
对于零散部分的贡献,即需要查询这个颜色是否在一条链上出现过
可以考虑使用O( sqrtn )修改,O( 1 )查询的可持久化树上前缀和,其实就是一个可持久化数组
于是可以计算零散部分贡献,每次查询的时候零散部分共O( sqrtn )个点
这样时间复杂度O( msqrtn ),空间复杂度O( nsqrtn ),(空间复杂度其实是O( n^(1+eps) ))
简单的例题
[Ynoi2010]D1T2
序列
1.区间染色
2.区间选出两个数相等的方案数
Solution
这题不弱于小Z的袜子,而小Z的袜子双向规约矩阵乘法,故难以polylog解决
考虑分块
大概的思想
使用一个数组A[i][j]来表示第i个块对第j个块的答案
这里表示的意思是从第i个块中选出一个数,第j个块中选出一个数,相等的方案数
Solution
先对原序列分块
考虑区间染色的颜色段均摊,对块进行分类
不妨设询问数和序列长度均为B^2;(可以理解为B=sqrtn)
将序列分为B块,每块大小为B;
每个块有两个状态:
状态1:块由一些段组成,每段内颜色相同
状态2:整个块只有一种颜色
题解
在状态1表示的块中,维护一个序列表示依次出现的段的颜色、长度
在状态2表示的块中,维护块的颜色
Solution
记A(x,y),x记B[x]为块x内选取两个元素,颜色相同的方案数。
记t[x,y]表示块x中颜色y的元素个数,以t[1..x,y]的和的形式记录。
Solution
接下来考虑几个基本操作:
(a).在状态1表示下,块x中颜色y的元素个数增加了z;
A[x,x']+=t[x',y]*z
B[x]+=t[x,y]*z+z*(z-1)/2
t[x,y]+=z
复杂度:由于枚举 x’,所以复杂度是O( B )的
Solution
(b).将一个块x染色为y,并变为状态2表示;
如果x在状态1,使用不超过B次(a)将块内所有颜色清空;
将x设为状态2,并记录颜色为y,修改B数组。
(c).将一个块x从状态2表示变为状态1表示;
使用一次(a)即可。
Solution
用基本操作可以组合出题目需要的预处理,修改和查询:
(1).预处理
可以将每个块初始置为空,转为不超过B^2次区间染色。
Solution
(2).区间染色
区间染色需要在区间端点所在的块进行(a)(c)操作并维护段的情况,在完整块进行(b)操作;
由于每次区间染色只增加O(1)段,操作(a)的次数是均摊O(1)的。
操作(b)(c)除去调用(a)的情况,时间复杂度为O(1)。
每次(a)操作涉及到A1[x,*],A2[*,x],t[x,y]的修改,修改后重新计算前缀和,时间复杂度为O(B)。
Solution
(3).区间查询
对于类型1的完整块之间的贡献,需要查A的矩形和(转为A中O(B)次区间和,差分可得),以及B的区间和;
统计零散部分和类型2的块中,查出每种颜色的出现次数,并查询t数组的区间和,这里我们对t数组建一个前缀和可以答案都查询复杂度单次O(1),即维护块前缀和,可以得到其余的贡献。
综上,时空复杂度均为O(B^3)。
[Ynoi2011]D1T1
序列
1 x y z : a[y] , a[y+x] , … a[y + kx] += z,这里y + (k+1)x > n,且y < x
2 l r : a[l] + a[l+1] + … + a[r]的和
Solution
若x n ,则我们暴力给每个位置加,需要加的次数为O( sqrtn )次。由于需要查询区间和,用分块维护,总修改、查询复杂度为O( msqrtn )。
若x < sqrtn ,我们需要用另外的方法维护。
注意到单次修改是针对整个序列的元素,所以对x,y相同的修改,我们可以累加它的贡献。
Solution
我们对每个x,维护y的前缀、后缀和。对于一次询问,我们可以当成把序列分成了若干个大小为x的块。
中间的整块元素,每个块里肯定所有的y都有,增加的贡献就是关于x的修改总和。所有块的贡献相同,可以O(1) 算。
边角的话,由于我们记录了前缀、后缀和,也可以O(1) 算。两个端点在同一个块中,则直接前缀和相减即可。
总时间复杂度 O( msqrtn )
[Ynoi2011]D2T2
给你一个长为 n 的序列,有 m 次查询操作。
每次查询操作给定参数 l,r,b,需输出最大的 x,使得存在一个 a,满足 0≤a如果不存在 [0,a-1]内的数,则输出 0。
Solution
考虑对b的大小进行根号分治
对较大的b,我们考虑莫队维护出区间的bitset A
然后把这个bitset每b个为一组
初始是一个大小为b的,全1的bitset B
然后每次and上我们目前A最前b位,然后A >>= b
这样当我们B == 0时,相当于找到答案了
时间复杂度O( nsqrtm + nm/b + nm/w )
Solution
对于比较小的b,可以对每个b跑一次莫队,这里分别维护b个bitset,第x个bitset表示mod b=x的元素
每次对这b个bitset找第一个0即可
这部分的时间复杂度为O( nsqrt(bm) + nm/w )
总时间复杂度O( nm/w )
CodeForces 840E. In a Trap
一棵树,点有点权ai,每次查询u到v路径上的max(ai xor dis(i,v)),保证u是v的祖先。
值域是[0,65536]
Solution
注意到值域很小,从这里入手,由于题太多讲不完就留作作业吧
[Ynoi2012]D2T2
给你一棵边权为 1,且以 1 为根的有根树,每个点有初始为0的点权值,定义两个点的距离为其在树上构成的简单路径的长度,需要支持两种操作:
1 a x y z:把 a 子树中所有与 a 的距离模 x 等于 y 的节点权值加 z。
2 a:查询 a节点的权值。
2019 Multi-University Training Contest 8 G
Solution
这个问题的形式目前我并不会polylog,于是考虑根号分治
考虑对于每次修改,如果x大该如何维护
可以对原树按照深度分层,每层的节点按照在原树的DFS序上的位置排序,转换为在n / x层上区间加
需要O( 1 )进行区间加,和找出每层在哪个区间进行区间加
前者平凡,使用一个O( 1 )区间加O( sqrtn )查询单点的分块即可,后者需要一些技巧性的方法
Solution
可以根号重构,每次对原树进行长链剖分,维护合并上来的每个节点每个深度的DFS序最小位置和DFS序最大位置
我采用了一个更好的做法:
记每个节点的深度为dep,DFS序上所对应的区间左端点为l,右端点为r,自己在DFS序上的位置为l
建立两个新的森林F1,F2
F1中x向y连边当且仅当dep[y] = dep[x] + 1 , l[x] < l[y] , 且l[y]最小
F2中x向y连边当且仅当dep[y] = dep[x] + 1 , l[x] > r[y] , 且r[y]最小
Solution
可以证明一个节点a在F1上的k层祖先即为节点a在原树子树中深度比其大k的所有节点里面DFS序最小的节点,在F2上的k层祖先即为节点a在原树子树中深度比其大k的所有节点里面DFS序最大的节点
于是我们可以通过在这两个森林中找k祖先来找到我们需要加的区间,这里可以每次批量找n / x个区间的端点,O( logn + n / x )在轻重链剖分结构上找出即可
于是可以O( sqrtn + n / x )解决
Solution
考虑对于每次修改,如果x小该如何维护
可以对每个x,将原树按照深度mod x进行分层,每次查询的节点对于每个x只会出现在一层中,于是需要查询x次
对于每个x,对于每个0...x-1的余数,将其按照DFS序排序,这里按照DFS序枚举就可以O( n )达成,子树修改即变成区间加
这样可以使用一个O( sqrtn )区间加O( 1 )查询单点的分块维护,这里区间的左右端点可以二分得到
于是可以一次O( nx )的预处理加上单次复杂度O( sqrtn + x )解决
在x=sqrtn处进行根号分治,即总时间复杂度O( (n + m)sqrtn ),空间复杂度O( n + m )
Hdu 6615
There is a tree with vertex 1 as a root. All vertices of the tree are colored.
Your task is to determine the number of sub-trees with exactly k distinct colors.
There are two types of queries.
1 u c : paint vertex u with color c.
2 k : answer the query.
2019 Multi-University Training Contest 4
Solution
每个点维护子树颜色个数
将x位置颜色从y改到z
对每个颜色维护子树中其出现的次数
每次修改一个位置的颜色则相当于O(1)次链+1-1的操作
相当于链+1-1,全局x出现次数
Solution
这个形式强于区间+1-1区间0个数,这个我们目前认为难以polylog解决,考虑分块
对原树进行树分块,维护簇路径的值域数组,表示簇路径上每个值出现次数
然后对簇路径的操作可以O(1)完成,又只有O( sqrtn )个零散的点
总时间复杂度O( msqrtn ),空间复杂度可以做到O( n + m )
[Ynoi2013]D1T2
Solution
对原序列建一棵线段树,考虑怎么在线段树上面修改和查询
定义 极长 “X” 段为一个极长的子区间,使得区间中符号均为乘法
区间值修改
回忆起前面一个莫队题的性质,这道题中同样存在:
维护出区间中每个极长的 “X” 段的长度,可以发现这个存在一个自然根号:
假设区间长度为size,则最多只有O( sqrt( size ) )种极长 “X” 段的长度
每次对区间进行值修改的时候,即对这个长度为O( sqrt( size ) )的多项式进行插值,暴力计算即可,插值复杂度为O( sqrt( size ) ),即可以O( sqrt( size ) )的时间将一个节点值进行修改,同时维护信息
区间符号修改
每次对区间符号进行修改的时候,区间的信息只会变成区间和或者区间乘积,所以我们每个节点要维护区间和和区间乘积
符号修改之后,这个节点的极长 “X” 段只会有O( 1 )种了
符号进行修改可能影响一些节点的极长 “X” 段,考虑如何维护这个
区间符号修改
对一个节点,我们可以归并两个儿子的极长 “X” 段,来维护出这个节点的极长 “X” 段
对一个大小为size的节点进行归并,代价是O( sqrt( size ) )的
注意需要特判左儿子的最右极长 “X” 段是否和右儿子的最左极长 “X” 段进行合并
区间信息合并
合并区间信息的时候,只需要把左右儿子信息加起来,同时特判O(1)个位置即可
这O(1)个位置就是左儿子的最右部分和右儿子的最左部分
可以处理:
标记对标记的影响
标记对信息的影响
信息和信息的合并
所以我们正确性有保证了
Complexity
我们所有地方的复杂度都是O( sqrt( size ) )的
线段树在每层只会递归到2=O(1)个节点中,所以每层只有O(1)个节点的信息需要更新
Complexity
T( n ) = T( n / 2 ) + O( sqrtn )
sqrt( n ) + sqrt( n /2 ) + sqrt( n / 4 ) + … + sqrt( 1 ) = O( sqrtn )
空间:
T( n ) = 2T( n / 2 ) + O( sqrtn )
sqrt( n ) + 2sqrt( n / 2 ) + 4sqrt( n / 4 ) + … + nsqrt( 1 ) = O( n )
总时间复杂度O( msqrtn ),空间复杂度O( n )
CF700D Huffman Coding on Segment 3100
给一个长为n的串,有q次询问,每次询问一个区间的最小二进制编码长度,即在可以唯一还原的前提下,将这一段子串转化为长度最小的二进制编码。
Solution
哈夫曼编码就是把每个出现过的元素提出来,按照出现次数加权,做合并果子
哈夫曼树在排序后可以做到线性
维护两个队列,第一个是初始的所有排好序的元素,第二个保存合成的所有元素,初始为空
每次从每个队列中选前2大的元素,找最小的两个合成,合成后放入第二个队列末端
Solution
有一个性质是不同的出现次数是O(sqrtn)的,考虑1+2+…+n=n(n+1)/2
考虑使用莫队维护出区间每个数的出现次数,从小到大排序
这个有多种维护方法,我之前写过的方法是记录下莫队转移时所有变化,然后到一个查询区间时一起处理掉,用莫队上一个处理的询问维护的区间不同的出现次数,以及记录的转移,得到这个区间的所有出现次数
时间复杂度O(nsqrtm+msqrtn)
Solution
这里考虑可以批处理同一个出现次数出现很多次的情况
如果当前最小是相同的x个a,则可以合并出x/2个2a
我们边维护两个队列边缩点
复杂度分析:
每O(1)次合并,下一次可能合并出的元素大小至少变大1
经过O(sqrtn)次合并,只可能合并出>sqrtn的元素了
而这两个队列如果均>sqrtn,则有O(sqrtn)个元素
每次合并减少一个元素,此时合并O(sqrtn)次
时间复杂度O(nsqrtm+msqrtn)
[Ynoi2013]D2T2
给一个长为 n 的序列,有 m 次查询操作。
查询操作形如 l r L R,表示将序列中值在 [L,R] 内的位置保留不变,其他的位置变成 0 时,序列中 [l,r] 区间内的最大子段和,这个子段可以是空的。
Solution
先研究全局查询的情况,考虑离散化后所有值域区间对应的不同的序列只有O( n^2 )种,我们可以分治来维护两边的最大前缀和,最大后缀和,最大子段和。
合并的时候,左儿子有个答案矩阵,右儿子也有个同规模的答案矩阵,我们把这两个稀疏化一下(大概就是说你每次把块内存在的值归并上来,这个矩阵会变大常数倍),然后就可以合并了,每次合并的是O( n^2 )的
所以这里我们有T( n ) = 2T( n / 2 ) + O( n ^ 2 ),解得T( n ) = O( n ^ 2 )
Solution
我们先在外层对序列分块,这样有O( sqrtn )个O( sqrtn )大小的块,每个块的分治预处理代价是T( sqrtn ) = O( n )的,所以预处理的总复杂度是O( sqrtn ) * O( n ) = O( nsqrtn )的
我们对序列每个块逐个处理,然后每次合并出答案即可
时间复杂度O( (n + m)sqrtn ),空间复杂度O( n + m )
[Ynoi2014]空の上の森の中の
线段树是一种特殊的二叉树,满足以下性质:
每个点和一个区间对应,且有一个整数权值;
根节点对应的区间是 [1,n];
如果一个点对应的区间是 [l,r],且 l如果一个点对应的区间是 [l,r],且 l=r,那么这个点是叶子; 如果一个点不是叶子,那么它的权值等于左孩子和右孩子的权值之和。
珂朵莉需要维护一棵线段树,叶子的权值初始为 0,接下来会进行 m 次操作:
操作 1:给出 l,r,a,对每个 x 将 [x,x] 对应的叶子的权值加上 a,非叶节点的权值相应变化;
操作 2:给出 l,r,a,询问有多少个线段树上的点,满足这个点对应的区间被 [l,r] 包含,且权值小于等于 a。
Solution
可以证明这个线段树只有O( logn )种不同大小的节点
对于每种节点大小分层,维护一个数据结构,支持:
1.区间加
2.单点修改
3.区间rank
这个是一个经典问题,目前上界是O( msqrtn ) ,我们通过一些规约证明了这个问题不弱于一个 sqrtn*sqrtn 的矩阵乘法,所以目前认为难以达到O( n*polylogn ) 的复杂度
Solution
可以证明线段树的每层只有O(1) 种不同大小的节点,那么我们的总时间复杂度是
O( msqrtn + msqrt(n/2) + msqrt(n/4) + … ) = O( msqrtn )
空间复杂度可以通过一些trick做到O( n + m )
[Ynoi2016]D1T1掉进兔子洞
有 m 个询问,每次询问三个区间[l1,r1] [l2,r2] [l3,r3]
记f( x , l , r ) 表示区间 [l,r] 中x的出现次数
查询:sum( i = 1 to n ) min( f( i , l1 , r1 ) , f( i , l2 , r2 ) , f( i , l3 , r3 ) )
Brute
先考虑如果每个数不相同怎么做
莫队跑出每个区间的值域bitset,然后&起来,这些就是被删掉的数了
Solution
想办法转换一下
先离散化,假设数x离散化后的位置是y,然后x出现z次
那么y,y+1…y+z-1这些位置都是x的
莫队维护区间bitset的时候
假设区间中y出现了w次
则我们把y,y+1…y+w-1这些位置填上1
y+w…y+z-1这些位置填上0
Solution
用这样处理过的bitset,&起来
&后得到的bitset里面的1的个数就是删掉的所有数了
总复杂度O( nsqrt(m) + nm/w ) = O( nm/w )
Note
这里为了方便,每次只给了三个区间,所以理论上来说可以跑一个6维的莫队,但我可以每次给任意k个区间,这样的算法复杂度就会变成O( n^(2-eps) )
[Ynoi2017]D1T1由乃的玉米田
序列,每次给参数l r c
查区间[l,r]是否可以选出两个数a,b使得:
a+b=c
a-b=c
a*b=c
a/b=c
值域1e5
除法是整除,也就是说 3/2 这种情况下认为二者不能除
Solution
Solution
Solution
假设新的右端点是r,上面的值是x
则对于每个x的的约数y,y最近一次出现的位置l到现在的右端点位置r
包含[l,r]这个区间所有区间都可以选出(x,y)这一对数使得其比利为x/y
于是我们根据这个扫描线即可,要扫两遍
复杂度是c的约数个数
Solution
对于-操作
维护区间的值域上的bitset
每次如果bitset & ( bitset << c )后不是0
则找到两个数a,b使得a-b=c
本质为用bitset优化了bool数组的匹配
然后就可以莫队维护区间的值域bitset了
加操作维护一个反的bitset即可
Solution
+的复杂度:O( nsqrt(m) + vm/w )
-的复杂度:O( nsqrt(m) + vm/w )
*的复杂度:O()
/的复杂度:O()
存在理论复杂度更优的做法,但是常数较大而not practical
矩阵乘法相关规约
Why
为什么这些题我们要用分块来处理?不能分治吗
Reason
很多分块题是不弱于sqrtn*sqrtn大小的矩阵乘法的
由于目前矩阵乘法上界只做到了O( n^2.373 ),所以目前技术做这些分块题无法低于O( n^(1+x) ),x is const,x > 0
目前有规约的问题
小Z的袜子(区间每个数出现次数平方和):双向规约01矩阵乘法,已经低于了O(n^1.5)
区间逆序对:双向规约01矩阵乘法,已经低于了O(n^1.5)
区间众数:单向规约布尔矩阵乘法,已经低于了O(n^1.5)
链颜色数:单向规约01矩阵乘法
目前有规约的问题
区间出现次数奇数次的数个数:单向规约01矩阵乘法
区间最大的|i-j|满足ai==aj:单向规约max-plus矩阵乘法(好像是)
区间加,区间小于x的数个数:单向规约01矩阵乘法
区间加,区间kth :单向规约01矩阵乘法
例子
假设给你一个黑箱,可以解决链颜色数问题,如何用这个黑箱来解决01矩阵乘法?
指Ans[i][j] = sum_k A[i][k] * B[k][j],值是[0,1]中的整数
规约
我们可以构造一棵:
根有sqrtn叉,下面接了sqrtn条链的树,总共sqrtn种权值
每次选出前sqrtn/2条链,和后sqrtn/2条链,总共有O( n )种不同的询问,询问这些链的并的颜色数
记:
A[i][j]表示第i条链是否有第j种颜色,这里iB[k][j]表示第k条链是否有第j种颜色,这里k>=sqrtn/2
规约
可以发现我们的询问即
Ans[i][j] = sum_k A[i][k] | B[j][k]
令C = B^T
则
Ans[i][j] = sum_k A[i][k] | C[k][j]
规约
由于值域是01,所以&和*等价,把每个数取反之后|就变成&了
所以
Ans[i][j] = sum_k A[i][k] * C[k][j]
我们通过这个黑箱实现了sqrtn*sqrtn 01矩阵的矩阵乘法
注意到这里规约是单向的,也就是说我们无法依靠快速矩阵乘法来得到低于O( n^1.5 )的链颜色数算法
大分块
目前最复杂的根号数据结构题
[Ynoi2018]未来日记
最初分块
2017 Multi-University Training Contest 4 M
给你一个序列
1.区间所有x变成y
2.区间kth
[Ynoi2018]未来日记
对这题的评价:8-9/11
Solution
先考虑如何求区间第k小值。对序列和权值都进行分块,设bi,j表示前j块中权值在i块内的数字个数,ci,j表示前j块中数字i的出现次数。那么对于一个询问[l,r],首先将零碎部分的贡献加入到临时值域分块数组tb和tc中,然后枚举答案位于哪一块,确定位于哪一块之后再暴力枚举答案即可在O( sqrtn )的时间内求出区间第k小值。
这个做法类似于在可持久化Trie上一起二分来查询区间kth,不过是在分块结构上一起跑来进行查询。
Solution
接着考虑如何实现区间[l,r]内x变成y的功能。显然对于零碎的两块,可以直接暴力重构整块。对于中间的每个整块,如果某一块不含x,那么无视这一块;否则如果这一块不含y,那么只需要将x映射成y;否则这一块既有x又有y,这意味着x与y之间发生了合并,不妨直接暴力重构整块。因为有c数组,我们可以在O(1)的时间内知道某一块是否有某个数。
Solution
考虑什么情况下会发生重构,也就是一个块内发生了一次合并的时候。一开始长度为n的序列会提供O(n)次合并的机会,而每次修改会对零碎的两块各提供一次机会,故总合并次数不超过O(n+m),而每次合并的复杂度是O( sqrtn )的,因此当发生合并时直接重构并不会影响复杂度。
Solution
那么现在每块中的转换情况只可能是一条条互不相交的链,只需要记录每个初值转换后是什么,以及每个现值对应哪个初值即可。遇到查询的时候,我们需要知道零碎部分每个位置的值,不妨直接重构那两块,然后遍历一遍原数组a即可得到每个位置的值。
在修改的时候,还需要同步维护b和c数组,因为只涉及两个权值,因此暴力修改j这一维也是可以承受的。
总时间复杂度O( (n+m)sqrtn ),空间复杂度O( nsqrtn )
Solution
这题主要的思路就是通过对序列和权值一起进行分块,然后让序列分块的O( sqrtn )部分乘上值域分块的O( 1 )部分,序列分块的O( 1 )部分乘上值域分块的O( sqrtn )部分,从而达到了复杂度的平衡。
[Ynoi2018]五彩斑斓的世界
第二分块
Codeforces 897 E
1 l r x : 把区间[l,r]所有大于x的数减去x
2 l r p : 查询区间[l,r]内的x的出现次数
值域1e5
[Ynoi2018]五彩斑斓的世界
对这题的评价:6/11
Solution
这个值域1e5很明显复杂度和值域有关
Solution
考虑分块,可以发现每块的最大值总是不增的
总的所有块的最大值和当块大小为O( sqrt(n) )时为O( nsqrt(n) )
(假设值域和n同阶)
考虑怎么利用这个性质
Solution
可以发现:假设区间所有大于x的减x,最大值为v
这个操作等价于把区间中所有数减x,之后小于0的再加x
当v >= x * 2时,可以把所有[1,x]内的数合并到[x+1,x*2]上
当v < x * 2时,可以把所有[x+1,v]内的数合并到[1,v-x]上
Complexity
如果v >= x * 2
我们用O( x ) * O( 数据结构复杂度 ) 的代价使得块内的最大值减少了O( x )
如果v < x * 2
我们用O( v - x ) * O( 数据结构复杂度 )的代价使得块内的最大值减少了O( v - x )
Solution
所以要用一个数据结构支持:
O( 1 )把块内值为x的全部变成x+v或者x-v
O( sqrt(n) )求出块内经过大量操作后,每个数的值
第一种是整块操作的时候要用
第二种是重构零散块的时候要用
Solution1
维护这个有很多种方法
可以每块维护一个值域上的链表
定义f[i][j]为第i块里面所有值为j的数的下标的链表
区间所有x变成x+v即link( x , x + v )
然后维护一下块内可能出现的所有数
每次重构的时候即遍历所有可能出现的数,然后遍历其中真正出现的数的链表即可
Solution1
不过链表常数巨大。。。
这个应该跑的很慢
Solution2
可以每块每个值维护一个vector
然后启发式合并这个vector
这个做法由于对缓存友好,所以会跑的快一些
Solution3
可以用一个并查集维护
这个并查集由于只支持:
1. merge( x , y )
2. for( i = 1 ; i <= sqrtn ; i++ ) find( i )
所以复杂度是O( 1 )的并查集
本质上和链表的做法是差不多的,不过常数好很多
时间复杂度O( (n+m)sqrtn ),空间复杂度O( nsqrtn )
[Ynoi2019]Another
[前]第三分块
树,每个点有编号
1.改一条边的边权
2.查询一个点到一个编号区间[l,r]的点的距离和
[Ynoi2019]Another
对这题的评价:5/11
Solution
对点的编号序列分块
考虑维护f(j,i)表示dfs序为i的点到前j个块的距离和
修改一条边的边权的时候,看造成什么样的影响:
Solution
只可能是红色的点和绿色的点之间互相影响
枚举前i块,可以O( 1 )知道第i块里面有多少在红色的部分里面,设这个为x
于是对dfs序在绿色部分的所有i,把f(j,i)加上x*修改的v,相当于我们要对f再做一个O( 1 )修改O( sqrtn )查询的分块结构
Solution
查询的时候,我们要查点i到[l,r]的贡献,就找离l和r分别最近的两个块端点,然后O( sqrtn )查出i到这两个前缀块的答案,然后把这两个差分一下
于是我们解决了整块的答案,考虑怎么查询零散
Solution
零散部分每次有O( sqrtn )个两点间距离和
然后现在考虑怎么快速查两个点之间的距离和
dist(i,j) = dep[i] + dep[j] – 2 * dep[ lca(i,j) ]
每次改变边权,相当于对dfs序的一段进行区间加,于是我们对dfs序再次分块,实现一个O( sqrtn )区间加,O( 1 )查单点的平衡
使用O( 1 )lca的话,我们就可以O( 1 )计算两点之间的dist了
于是问题得到解决
时间复杂度O( (n+m)sqrtn ),空间复杂度O( nsqrtn )
[Ynoi2018]天降之物
第四分块
51nod 算法马拉松35
序列a
1.把所有x变成y
2.查询最小的|i-j|使得ai==x,aj==y
[Ynoi2018]天降之物
对这题的评价:5/11
Solution
考虑根号分治
定义一个值x出现次数为size[x]
如果没有修改操作,则预处理所有size大于sqrtn的值到所有其他值的答案,以及每个值出现位置的一个排序后的数组
查询的时候如果x和y中有一个是size大于sqrtn的,则可以直接查询预处理的信息,否则进行归并
O( nsqrtn + msqrtn )
Solution
有修改操作即在这个做法上改良,因为发现这个做法的根号平衡并没有卡满,所以有改良余地
假设把所有x变成y
由于可以用一些技巧使得x变成y等价于y变成x,所以不妨设size[x] < size[y]
定义size大于sqrtn为大,size小于等于sqrtn为小
定义ans[x][y]为x到y去除附属集合的部分的答案(附属集合是什么下面有说)
x取遍所有值,y只有所有大的值,总O( sqrtn )个
Solution
修改:
如果x和y均为大,则可以暴力重构,O( n )处理出y这个值对每个其他值的答案,因为这样的重构最多进行O( sqrtn )次,所以这部分复杂度为O( nsqrtn )
如果x和y均为小,则可以直接归并两个值的位置的排序后的数组,单次O( sqrtn ),所以这部分复杂度为O( msqrtn )
如果x为小,y为大,发现小合并进大的均摊位置数为O( n ),对这个再次进行根号平衡
对于每个大,维护一个附属的位置集合,这个位置集合的大小不超过sqrtn
每次把小的x合并入大的y的时候,即合并入这个附属集合,并且用x到所有大的值的答案更新y到所有大的值的答案,这样
如果合并后附属集合大小超过sqrtn,则O( n )重构y到所有值的答案,这个过程最多进行O( sqrtn )次,均摊复杂度O( nsqrtn )
由于大的值个数 <= sqrtn , 附属集合大小 <= sqrtn,这一部分是单次O( sqrtn )的,所以这部分复杂度为O( msqrtn )
Solution
查询:
如果x和y均为大,则在维护的答案中查询min( ans[x][y] , ans[y][x] ),然后将x的附属集合和y的附属集合进行归并,这一部分是单次O( sqrtn )的,所以这部分复杂度为O( msqrtn )
如果x和y均为小,则进行一次归并即可,所以这部分复杂度为O( msqrtn )
如果x为小,y为大,则在维护的答案中查询ans[x][y],然后将x和y的附属集合进行归并,这一部分是单次O( sqrtn )的,所以这部分复杂度为O( msqrtn )
由于维护了所有可能的贡献,而且更新是取min,正确性也得到了保障
时间复杂度O( (n+m)sqrtn ),空间复杂度O( nsqrtn )
Solution
存在序列分块的做法
[Ynoi ]
第五分块
未知
[Ynoi2018]末日时在做什么?有没有空?可以来拯救吗?
第六分块
序列
1.区间加任意数,在[-2^(w-1),2^(w-1)-1]内
2.查询区间最大子段和
[Ynoi2018]末日时在做什么?有没有空?可以来拯救吗?
对这题的评价:8/11
先看一个这题的弱化版
[Ynoi2015]世界で一番幸せな女の子
维护序列支持:
1.全局加
2.区间最大子段和
Solution1
由于可以加负数
设pre[x]为x时刻全局加的值
按照pre从小到大处理
这样就转换为了只加正数
Solution1
考虑分块
每块维护一下块内长为1…sqrt(n)的最大前缀,最大后缀,最大子段和
如果一个整块加了,那么这个整块块内的最大子段长度肯定是不降的
Solution1
每次查询的时候按照当前的全局加标记确定出每个块内的最大子段和
然后把跨块的询问用左边块的最大后缀和右边块的最大前缀拼起来
即可
总复杂度O( msqrt(n) + nsqrt(n) )
Solution2
这个根号太屑了,考虑polylog
Solution2
线段树维护:
每个节点的左,右,内部最大子段和的凸函数
凸函数是一个区间的半平面交,每个下标x对应的意义是这个节点被整体加了x后,该节点的左,右,内部最大子段和的值是多少
设左最大子段和是pre,右最大子段和是suf,内部最大子段和是mid
Solution2
然后建树的时候可以发现
cur -> pre[i] = max( cur -> left -> pre[i] , cur -> right -> pre[i] + cur -> left -> sum );
cur -> suf[i] = max( cur -> left -> suf[i] + cur -> right -> sum , cur -> right -> suf[i] );
cur -> mid[i] = max( cur -> left -> mid[i] , cur -> right -> mid[i] , cur -> left -> suf[i] + cur -> right -> pre[i] );
这个可以类比单点修改区间最大子段和理解
Solution2
我们来看看这个需要支持什么操作
需要支持:
1.把一个凸函数加上一个常数
2.求一个凸函数a,满足a[i] = max( b[i] , c[i] ),其中b,c为凸函数
3.求一个凸函数a,满足a[i] = b[i] + c[i],其中b,c为凸函数
Solution2
可以发现这三个性质都满足
而且可以通过归并两个儿子的凸函数来得到cur的凸函数
于是预处理复杂度O( nlogn )
每次查询的时候直接在线段树上查询区间即可
总复杂度O( (n+m)logn )
Solution
考虑把全局加区间最大子段和的做法拓展到区间加区间最大子段和:
先考虑加正数怎么做
如果朴素地来实现的话我们可以对序列进行分块,每块开一个数据结构
这样复杂度是O( (n+m)sqrt(nlogn) )的,因为整块的线段树可以均摊O( 1 )直接在根上打标记,主要是零散部分代价比较高
Solution
发现零散部分直接重构整棵线段树代价是O( slogs )的,过大
发现本题使用的线段树并不需要支持区间查询,只是一个分治结构而已
考虑每次修改的时候,对于每个被修改到的节点cur,只会有cur的一个儿子被修改
于是我们可以通过归并cur的两个儿子的凸函数信息来得到cur的新的信息,没有必要重构整棵线段树,只需要部分重构
Solution
由于归并复杂度是O( 节点大小 )的,而且每层只归并一个节点,所以零散部分修改复杂度变为了O( s + s / 2 + s / 4 + ... + 1 ) = O( s )
于是得到了一个时间复杂度均摊O( sqrtn )的算法
时间复杂度O( (n+m)sqrtn ),空间复杂度O( nlogn )
Solution
加任意数?
逐块处理
发现每次操作的零散块只有O(1)个,我们离线,然后逐个块处理,对每个块算出我们需要的信息即可,具体细节可能比较复杂
这样我们可以对每个块进行基数排序,把询问和点一起排序,让其从加任意数变成加正数
这里值域是Θ( m2^w ),由RAM的假设认为w=Θ( logn ),在这个假设下基数排序是线性的,所以我们同复杂度解决了加任意数
时间复杂度O( (n+m)sqrtn ),空间复杂度O( n + m )
[Ynoi2018]馱作
第七分块
THUPC 2019 A
无边权树
树上的一个邻域定义为到点x距离不超过y条边的点集,x称为邻域的中心,y称为邻域的半径。
给一棵n个点的树,m次询问,每次给出两个邻域,问两个邻域中各取一个点,两两点对间的距离之和 。
n,m≤100000
[Ynoi2018]馱作
对这题的评价:10/11
一些记号和定义
对于树上的顶点 a,b,顶点集 S,S1,S2,定义 d(a,b)表示顶点 a 到 b 的距离,若 a=b 则 d(a,b)=0,否则 d(a,b)是 a,b 间简单路径的边数; 另外定义
d(S,a) = d(a,S) = ∑ d(a,b)[b∈S]
d(S1,S2) = ∑ d(a,S2)[a∈S1] 。
树 T 上的一个邻域 NT(x,y)定义为到顶点 x 距离不超过 y 条边的顶点集。x 称为邻域的中心, y 称为邻域的半径。
Preknowledge
真实的树分块——Topology Cluster Partition
树分块将 n 个结点的树分成了一些块的并,满足下列性质:
1.每个块是树
2.每个块中有两个特殊的点,称为端点 1 和端点 2。
3.不同块的边集不相交
4.一个块中的顶点,除端点外,其余顶点不在其它块中出现
5.如果一个顶点在多个块中出现,那么它一定是某一个块的端点 2,同时是其余包含这个顶点的块的端点 1
6.如果把所有块的端点作为点,每块的端点 1 和端点 2 连有向边,则得到一棵有根树
Preknowledge
这里给出树分块的一个实现,满足块数和每块大小均为 O( sqrtn ):
在有根树中,每次选一个顶点 x,它的子树大小超过sqrtn,但每个孩子的子树大小不超过sqrtn, 把 x 的孩子分成尽可能少的块(以 x 为端点 1,但暂时允许有多个端点 2,且每块至多有 2sqrtn 个顶点),然后删掉 x 的子树中除 x 外的部分。重复直到剩下的点数不超过sqrtn,自成一块。 这样就求出一个保证块中顶点数和块数均为 O( sqrtn )的树分块(块间可以共用一些顶点,但每条边只属于一个块),如果一个块有多个端点(即被多个块共用的点),则在块内将这些端点 建出虚树,将虚树上的每条边细分为一个新的块,以保证最终每个块只有两个端点。
Solution1
如果只有单次询问,可以进行转化:
d(S1,S2) = ∑[d(a,c)*|S2|+d(b,c)*|S1| 2d(lca(a,b),c)][a∈S1,b∈S2],其中 c 是任意一个点。 这里我们取c为根节点,这样把两两顶点间的距离和转化为了点集内顶点的深度和以及两两顶点间 lca 的深度和:
d(S1,S2) = ∑[dep(a)*|S2|+dep(b)*|S1| 2dep(lca(a,b))][a∈S1,b∈S2]
对 lca 部分可以在 O(n)时间内求出:初始化树的边权为 0,将 S1 中的每个顶点到根的路径的边权+1,求 S2 中每个顶点到根的路径的边权和之和。
Solution1
首先进行树分块,方便起见,认为一个块包含块中除了端点 1 之外的点,这样每个点就恰好 属于一个块。 预处理每个块 B(端点为 a1,a2)中的 d(NB(ai,x),aj)(i,j=1,2),需要 O(n)时间和空间。
树 T 的一个邻域可以拆分为这个邻域和每个块的交。
对于块 B,若 x 在 B 中,则 NT(x,y)∩B=NB(x,y); 否则设 z 是 B 中距离 x 较近的端点,距离为 d,则 NT(x,y)∩B=NB(z,y-d)。
Solution1
求两个邻域间的距离和,只需考虑这两个邻域和每个块的交。求块 B1,B2 的两个邻域 n1=NB1(x1,y1)和 n2=NB2(x2,y2)间的距离和。 如果 xi 不是 Bi 的端点,则显式地求出 ni 以及 ni 到 Bi 的端点的距离和,这需要 O( sqrtn )的时间。
Solution1
当 B1≠B2 时,设 a 为 B1 中最靠近 B2 的端点,b 为 B2 中最靠近 B1 的端点,n1 和 n2 间的距离和 d(n1,n2)=d(a,b)*|n1|*|n2|+d(n1,a)*|n2|+d(n2,b)*|n1|。通过在块构成的树上 dfs,这部分可以在 O( sqrtn )时间内处理。
当 B1=B2 时,如果 x1 和 x2 都是 B1 的端点,每块每次询问这种情况出现至多 1 次,这里暂不考虑,最后再离线处理;否则每次询问这种情况只出现 O(1)次,可以 O( sqrtn )暴力处理。
Solution1
离线处理的部分,枚举每个块 B,再枚举询问(只需考虑两个邻域的中心都不在 B 中的询问) 计算贡献,有 O(n)个询问形如 d(NB(a,y1),NB(b,y2)),对的 4 种情况分别计算。由于块中 点数的限制,实际只有 O(n)种(y1,y2=O( sqrtn ))。 仍然转化为求两两点间 lca 的深度和,枚举 y1,维护初始边权为 0,将 NB(a,y1)中每个点到 根路径上的边权+1 后得到的树,此时每个 y2 对应的答案是 NB(b,y2)中每个点到根的路径的 边权和之和。这部分时间和空间都是 O(n)的。
时间复杂度O( (n + m)sqrtn ),空间复杂度O( n )
Solution2
本题还存在利用静态top tree(RC分治)来简化问题的做法,但是限于问题的复杂性还是只能做到O( (n + m)sqrtn )时间复杂度
[Ynoi ]
第八分块
未知
[Ynoi ]
第九分块
未知
[Ynoi2019]魔法少女site
第十分块
序列
1 x y : x位置修改为y
2 l r x : 查询区间[l,r]有多少子区间的max <= x
[Ynoi2019]魔法少女site
对这题的评价:6/11
Solution
这是带修改不删除莫队,首先这个问题是四维的,一维时间维,一维值域维,两维序列维,考虑莫队维护( 时间 , max )的二元组,数据结构维护序列维:每次离线处理O( sqrtn )个操作。
Solution
令x递增扫描,维护一个与原序列等 的01序列,其中一个位置为1当且仅当原序列中此处的值小于等于x且在这些操作中没有修改过这个位置,支持将0变成1,查询内每个段(定义段为01序列上的极 区间,满足区间内均为1)的贡献( 度*( 度-1)/2)。
Solution
当x与某个询问的x相同时,处理这个询问,对于在这个询问前被修改过的位置,需要将0变为1,处理完这个询问后撤销操作;另外还需要将位置暂时设为0,在询问结束后恢复。为支持上述操作,对每个由1组成的段,在段的两端记录这个段的另一端的位置,在将0变成1时可以O( 1 )维护段的变化情况。
Solution
使用分块实现O( 1 )单点加O( sqrtn )查询区间和,将每个段的贡献记录在段的左端点上,在段发生改变时动态维护。为了支持将位置暂时设为0(此时需要知道这个位置当前是否为0,若非0还需要知道这个位置所在的段的左右端点),还需要支持O( sqrtn )查询一个位置左边的第一个左端点,并在段发生改变时O( 1 )更新一个位置是否是某个段的左端点,这同样可以使用分块实现。
综上所述,可以在O( n )时间内处理O( sqrtn )个操作,总的时间复杂度为O( (n + m)sqrtn )。
[Ynoi2018]GOSICK
第十四分块
序列,值域和n同阶
每次给出一个区间[l,r],查询存在多少二元组(i,j)满足l <= i , j <= r,且ai是aj倍数
[Ynoi2018]GOSICK
对这题的评价:8/11
Solution
我们考虑莫队维护,不失一般性这里只讨论莫队的四种拓展方向里面的一种
每次把区间[l,r]拓展到[l,r+1]的时候需要维护a[r+1]和[l,r]这段区间的贡献
这里利用莫队二次离线的trick:
莫队就可以抽象为nsqrtm次转移,每次查询一个序列中的位置对一个区间的贡献
这个贡献是可以差分的, 也就是说把每次转移的a[r+1]对区间[l,r]的贡献差分为a[r+1]对前缀[1,r]的贡献减去对前缀[1,l-1]的贡献
Solution
然后通过这个差分我们可以发现,我们把O( nsqrtm )次的修改降低到了O( n )次修改,因为前缀只会拓展O( n )次
于是我们每次可以较高复杂度拓展前缀和,因为插入次数变成了O( n )次
然后这 我们离线莫队的转移的时候可以做到线性空间,因为每次莫队是从一个区间转移到另一个区间:
我们记下pre[i]为i的前缀区间的答案,suf[i]为i的后缀区间的答案
Solution
不失一般性,只考虑把区间[l1,r1]拓展到区间[l1,r2]:
[l1,r1]区间的答案为红色部分的贡献,[l1,r2]区间的答案为红色部分加上绿色部分的贡献,r2的前缀贡献为所有的贡献,r1的前缀贡献为红色的贡献与前两个蓝色的贡献
于是我们可以把绿色的贡献,也就是两次询问的差量差分为pre[r2]-pre[r1]-{[1,l1-1]对[r1+1,r2]的贡献}
Solution
这里每个位置开个vector存 下就可以了,相当于说在l1-1位置push_back( pair < int , int > ( r1 + 1 , r2 ) ),然后扫描线扫到的时候直接暴力进行处理就可以了
于是我们达成了O( n + m )的空间复杂度将莫队给 次离线
现在考虑怎么算这个贡献,我们要高效计算区间[l,r]对x的贡献时
先把贡献拆开变成:[l,r]中x的倍数个数,[l,r]中x的约数个数
Solution
[l,r]中x的倍数个数:每次前缀加入一个数a[i]的时候,我们把a[i]的约数位置所对应的数组pre1的位置都++然
后查询的时候直接查pre1[x]即可得到x倍数个数
[l,r]中x的约数个数:这里考虑对x的约数进行一次根号分治
Solution
对于所有x 于sqrtn的约数,我们拓展前缀的时候维护,即每次把a[i]的倍数位置所对应的数组pre2的位置都++
然后查询的时候直接查pre2[x]即可得到x大于sqrtn的约数个数
对于所有x小于sqrtn的约数,我们考虑每次直接枚举区间[l,r]中1,2,...sqrtn的出现次数
这里可以先枚举1,2,...sqrtn,然后预处理一个前缀和,O( n + m )算出对每个询问的贡献,从而节省空间
于是我们得到了 个总时间复杂度O( n( sqrtn + sqrtm ) ),空间O( n + m )的做法
Thanks for listening
根号数据结构
信息学奥林匹克竞赛知识点(难点)精讲——数据结构【尖端】
Notice
如果没有专门说明
默认n = 1e5 , m = 1e5
分块基础
分块的分类
静态分块
动态分块
静态分块指的是放一些关键点,预处理关键点到关键点的信息来加速查询的,不能支持修改
目前认为:如果可以离线,静态分块是莫队算法的子集
动态分块指的是把序列分为一些块,每块维护一些信息,可以支持修改
动态分块基础
下列提到的分块默认为动态分块
分块基础
要实现:
1.区间加
2.区间和
朴素来做,可以有O(1)修改O(n)查询以及O(n)修改O(1)查询的暴力做法
这个问题可以套用根号平衡达到O( sqrt(n) )修改O( sqrt(n) )查询
我们可以把sqrt(n)个元素放一块里面维护
分块基础
我们把每次操作完整覆盖的块定义为“整块”
把每次操作没有完整覆盖的块定义为“零散块”
分块基础
每次操作最多经过O( sqrt(n) )个整块,以及2个零散块
所以我们可以O(1)维护整块信息,O( sqrt(n) )查询零散块信息
这样就达到了O( msqrt(n) )的复杂度
分块
一个度数 ,只有三层的树
分块
每次修改只用更新: 个size为1的节点以及2个size为 的节点
注意到我们不用维护那个size为n的根节点的信息
分块的作用
所以如果在分治结构上很难快速合并某些信息,我们就可以利用分块来做
经典问题
Solution
如果是单点修改,我们可以用树套树实现
但是区间修改后树套树无法快速合并信息
比如我们维护了cur的一个名次数据结构
cur的左儿子没有发生变化
cur的右儿子被整体加了
这样我们无法通过这两个儿子的名次数据结构快速维护出cur的名次数据结构
也无法直接在cur的名次数据结构上操作
所以分治结构无法在低复杂度解决这个问题
Solution
分块,维护每块的OV(就是排序后的数组)
每次区间加的时候
整块可以打一个标记
零散块可以重构
每次查询的时候
整块查询小于x的数,这个整块的标记为y(也就是说这一块所有数都加了y)
则等价于查整块的排序后的数组里面小于x-y的数的个数
这个可以二分
零散块就直接暴力查询块内在查询区间内的数是否满足条件
Complexity
设有x个块
查询复杂度:
整块O( log(n / x) ) * x
零散块O( n / x )
修改复杂度:
整块O( 1 )
零散块O( n / x ) (重构的时候用归并)
按照根号平衡算一算可以发现
总复杂度O( msqrt( nlogn ) )
此时块大小为sqrt( nlogn )
Solution
大概有另外两个O( msqrt( n ) )的做法
不过没有什么太大的实用价值,写起来很麻烦,常数较大,不一定比O( msqrt( nlogn ) )做法快,也基本上没人会
所以这里就不讲了
[Ynoi2017] 由乃打扑克
Solution
Solution
Solution
Solution
存在O( msqrt( nlogn ) )的算法,基于复杂的多序列二分,not practical
用根号平衡来优化数据结构复杂度
根号平衡
根号平衡
根号平衡
修改:
查询:
根号平衡
根号平衡
分块维护块内前缀和和块外前缀和
也就是说维护每个块块内前x数的和
以及维护前x的块的和
更新的时候分别更新这两个前缀和
查询的时候把这两个前缀和拼起来
根号平衡
修改:
查询:
根号平衡
维护一个序列,支持:
O( sqrt(n) )区间加,O(1)查单点
根号平衡
直接分块
根号平衡
修改:
查询:
根号平衡
根号平衡
根号平衡
修改:
查询:
根号平衡
根号平衡
根号平衡
修改:
查询:
根号平衡
根号平衡
值域分块
对于每个数维护一下其在哪个块里面
对于每个块维护一个OV(有序表)表示这个块内的所有数存在的数,从小到大
这样我们修改的时候只会改变sqrt( n )个数所从属的块
查询的时候定位到其所属于的块,然后找到其在该块中对应的值
根号平衡
修改:
查询:
CodeChef Chef and Churu
给长为n的序列,给定m个函数,每个函数为序列中第li 到第ri个数的和
有q个两种类型的操作:
1 x y 把序列中的第x个数改为y
2 x y 求第x个函数到第y个函数的和
Solution
因为函数不变,所以把函数分块
维护一个前i个块的函数的前缀和,代表前i个块中每个序列上的点的出现次数
然后再维护一个前i个块的函数的答案
每次修改只需要查询这个序列上的点在前i个块的函数中的出现次数即可
然后零散的部分,即用一个O( sqrt(n) )修改,O( 1 )查询的分块维护即可
O( nsqrtn + msqrtn ) = O( msqrtn )
Solution
可能存在polylog做法,但我想了想不会,这里只是通过此题介绍一下分块
Luogu3863 序列
Solution
简单莫队算法
普通莫队算法
理想莫队信息:维护一个子集的信息,支持O( a )插入一个元素,O( b )删除一个元素,无法比直接暴力更高效地合并
问题:给出一个点集,多次询问点集的一个子集的信息
这里只考虑类似区间信息的维护
普通莫队的本质
假设有两个区间询问
[l1,r1],[l2,r2]
如果我们可以O(x)插入或者删除一个元素
即我们已经得到了[l,r]的答案
可以O(x)转移得到
[l,r+1],[l,r-1],[l-1,r],[l+1,r]的答案
那么我们可以O( x * ( |r1-r2|+|l1-l2| ) )
由[l1,r1]的答案得到[l2,r2]的答案
普通莫队的本质
于是序列长n,有m个询问
我们可以以一种特殊的顺序依次处理每个询问
使得sigma( |li-li-1| + |ri-ri-1| )在一个可以接受的范围内
可以对序列分块,然后把询问排序
排序的时候以左端点所在块编号为第一关键字
右端点位置为第二关键字
普通莫队的本质
可以证明这样的复杂度是O( nsqrt( m ) + m )的
普通莫队的本质
普通莫队的本质
有没有更优的做法呢
我们可以用曼哈顿距离最小生成树去近似这个问题
把每个询问[l,r]看做二维平面上的点
于是我们按照建出来的曼哈顿距离最小生成树去DFS
这个做法的复杂度和最优转移一定是同阶的
曼哈顿距离最小生成树和刚刚介绍的排序算法的最坏复杂度是一样的,所以莫队问题可以直接按块排序
普通莫队的优秀写法
普通莫队卡常数的基本方法
排序要按照奇偶分别排
这样可以块一倍
调那个常数可以块10%左右
经典问题
查询一个区间中每个数出现次数的平方和
Solution
裸上莫队,定义cnt[x]为x的出现次数
每次更新的时候,如果插入一个x
则ans += 2 * cnt[x] + 1
如果删除一个x
则ans -= 2 * cnt[x] – 1
Notice
此题存在O( n^1.41 )的算法,依赖快速矩阵乘法而not practical
[Ahoi2013]作业
Solution1
Solution1
Solution1
Solution1
Solution2
显然存在polylog解法,这里不做介绍
[Ynoi2016]这是我自己的发明
Hint
Solution
Solution
Bzoj3920 Yunna的礼物
Technology
Technology
Solution
Bzoj4241历史研究
序列,定义Chtholly(l,r,x)为x在区间[l,r]中出现次数,查询一个区间中最大的x*Chtholly(l,r,x)
Solution
[Ynoi2015]いずれその陽は落ちるとしても
Solution
考虑单次询问怎么算
对于数x,假设出现了y次,区间长度是len
则x对答案的贡献是
是除了x之外的数有这么多个不同的子序列,这些对x的贡献没有影响
是所有x构成的子序列中有 种至少包含一个x,有1种不包含x
Solution
Solution
注意到贡献分为两部分 与
其中第一部分非常好维护
第二部分的贡献,可以把出现次数相同的数一起维护贡献
注意到一个区间中只有O( sqrt( n ) )种不同的出现次数
Solution1
Solution2
Luogu3245 HNOI2016大数
给一个数字串以及一个质数p
多次查询这个数字串的一个子串里有多少个子串是p的倍数
Solution
记suf[i]为i -> n构成的后缀串
如果对于l,r有suf[l] % p == suf[r+1] % p
则s[l...r] * 10 ^ ( n - r - 1 )为p的倍数
Solution
对p=2,5时特判
p!=2,5时s[l...r] * 10 ^ ( n - r - 1 )为p的倍数即意味着s[l...r]为p的倍数
离散化一下,然后就变成小Z的袜子了
Luogu3604 美好的每一天
Solution
Solution
Solution
经典问题
查询区间逆序对个数
吐槽
Brute
Solution
为什么要维护区间树状数组?
Solution1
可以维护一个可持久化块状树
或者称为可持久化值域分块吧
可以理解为把分块的树可持久化一下
Solution1
根号平衡:
可持久化Trie:
O( logn )插入+可持久化
O( logn )查询区间小于x的数个数
可持久化块状树:
O( sqrtn )插入+可持久化
O( 1 )查询区间小于x的数个数
Solution1
But
Question
难道这个logn不可卡吗
Answer
Notice
此题存在O( n^1.41 )的算法,依赖快速矩阵乘法而not practical
莫队二次离线
莫队二次离线
莫队二次离线
具体实现:区间逆序对的Solution2
Problem
Possibility
可不可以优化这个的空间呢?
Optimization
如果可以把空间优化至O( n + m )
则一切问题都解决了
(时间消耗大的最大问题是空间太大导致内存访问代价过高引起的)
Optimization
深入挖掘这个莫队的性质
发现莫队只有O( m )次本质不同的询问:
区间[l1,r1-1]内与a[r1]有关的一个信息
区间[l1,r1-2]内与a[r1-1]有关的一个信息
区间[l1,r1-3]内与a[r1-2]有关的一个信息
......
区间[l1+1,r1]内与a[l1]有关的一个信息
区间[l1+2,r1]内与a[l1+1]有关的一个信息
区间[l1+3,r1]内与a[l1+2]有关的一个信息
......
Optimization
这个明显很有规律
可以针对莫队的4种转移推一下其贡献
发现有6种贡献:
+/-前缀x内序列区间为[l,r]的所有数的贡献
+/-前缀[l,r]内其右边+1位置的数的贡献
+/-前缀[l,r]内其自己的贡献
第一种可以直接在每个地方开个vector,然后push_back一个pair表示区间来实现
后面两种可以通过打差分标记来实现
Optimization
这个存在简洁很多的写法,讲后面的题的时候回提到
树上莫队
查询链信息
查询子树信息
如果是查询子树的理想莫队信息,那么子树信息可以启发式合并上来,是polylog的
树上莫队
查询链的信息
有多种实现方法
第一种是将树的联通块分块,在树上跑莫队
另一种是将树的括号序分块,在括号序上跑莫队
我们也可以使用更好的树分块方法,不过链太弱了所以没有必要
无论代码难度,常数来说都是括号序更优
这里只介绍括号序
括号序
即DFS树的时候
进入x点就push_back( +x )
走出x点就push_back( -x )
莫队转移的时候
如果新加入的值是+x,就加入x
如果新加入的值是-x,就删除x
如果新删除的值是+x,就删除x
如果新删除的值是-x,就加入x
带修改莫队
普通的莫队是在转移二元组状态(l,r)
如果带修改,可以加上一维表示时间
把状态变成三元组状态(l,r,t)
这个新的状态可以在一个可以O(1)转移到
(l,r,t-1) (l,r,t+1)
(l-1,r,t) (l+1,r,t)
(l,r-1,t) (l,r+1,t)
可以用和普通莫队类似的方法排序转移,做到O( n^5/3 )
不删除莫队
莫队转移需要可以在一个可以接受的复杂度达到:
由(l,r)转移到(l-1,r),(l+1,r),(l,r-1),(l,r+1)
然而有的信息不支持快速删除(比如max)
可以通过一些方法使得其只要支持按顺序撤销,而不用支持删除
经典问题
Brute
Possibility
Solution
Solution
Solution
Solution
Solution
整个的区间为[x,y]
蓝色的区间为[l,r]
即我们需要删除绿色的区间里面所有的数
Solution
考虑撒t个关键点
如果维护了关键点到关键点的信息
则我们[x,y]只要找到最近的关键点l满足l<=x,最近的关键点r满足y<=r即可O( n/t )从区间[l,r]转移到区间[x,y]
我们知道所有关键点的位置后
可以离线每个询问,就知道每个询问是由哪一对关键点得来的
Solution
Notice
Notice
Notice
这个题有nlognlogv的线段树做法
可以去cf上翻翻
Bzoj4358 permu
Solution 引用自ccz181078博客
CodeChef QCHEF
序列,每个询问求区间[L,R]中值相同时,位置差的最大值
即最大的|x-y|使得L<=x,y<=R且a[x]==a[y]
Solution
Luogu5386 [Cnoi2019]数字游戏
给定一个排列,多次询问,求一个区间 [l,r] 有多少个子区间的值都在区间 [x,y] 内。
Solution
这个题我们可以考虑用莫队跑值域区间
我们把值在目前莫队跑的区间内的序列位置标为1,否则标为0
发现答案就是在序列的一个区间中,每个极长1的段的size的平方,这样的东西
Solution
我们对序列分块后,每个块维护块内的答案,这样如果我们知道每次修改的极长1段的位置,我们就可以O(1)修改了
上面一题给出了一个不删除莫队维护极长1段的方法,直接套用就行了
总时间复杂度O( nsqrtm + msqrtn )
静态分块基础
下列提到的分块默认为静态分块
分块的本质
经典问题
给一个序列,每次查询一个区间的众数,强制在线
Solution1
之前几个题属于带修改的动态分块,这个题就属于只带查询的静态分块了
如何合并信息?
对于众数有一个性质:
如果x是集合A里面的众数,我们往集合A里面加入集合B里面的所有数
现在新集合的众数只会是x或者集合B里面的数
Solution1
序列上每隔根号个数放一个关键点
预处理每两个关键点之间的众数
这个可以以每个关键点为开头for一下序列实现
Solution1
查询的时候
我们已经预处理了黄色部分的众数了
只需要加入蓝色的点,蓝色的点只有 一个一个验证即可
Solution1
验证的时候需要快速查询一个数在一个区间中出现次数
如果用可持久化Trie来维护,单次查询O( logn )
总复杂度O( msqrt( n )logn )了
Solution1
注意到
我们只需要支持一个可持久化的数据结构
插入n次,查询msqrtn次
这个可以利用根号平衡
也就是说我们需要有一个可持久化的数据结构支持
O( sqrt( n ) )插入,O( 1 )查询
显然可以利用可持久化块状树(可持久化值域分块)实现
Solution1
还有另一个做法
即维护每个值在前i个块中的出现次数
这个数在第x到第y个块中出现次数
即为在前y个块中的出现次数减去前x-1个块中的出现次数
每次先把零散加进去
这样就可以O(1)查询一个数在区间中出现次数了
Solution1
通过用这个
可以做到复杂度
O( nsqrt( m ) )
Technology
这样的区间众数空间是O( nsqrt(n) )的
可以进行一次根号分治做到O( n^1.25 )
还有个论文方法可以做到空间O( n ),而且基本上没常数
Solution2
我们可以对每个值开个vector,记下每个位置在vector中的位置
可以发现,假设我们现在在x位置,我们目前众数出现次数为y,现在在从右往左边扫
那我们只需要check答案是否会增大1就可以了
那么就是vector[ belong(x) + y ]这个位置在不在区间[l,r]内部
这个我们可以O( 1 )找到,所以可以O( 1 )拓展
这样达成了线性空间
Technology
离线存在O( n^1.48541 )的算法,基于对max-plus形式的稀疏矩阵乘法的优化,not practical
经典问题
强制在线,查询区间逆序对
Solution
主要思想还是通过差分和归并来优化复杂度
考虑把序列分成sqrtn块
预处理任意两个关键点之间的信息
Solution
查询答案的时候:
答案为l和r整块内的贡献
加上两个零散块对整块块内贡献
加上零散块之间贡献
红色为整块内贡献
绿色为两个零散块对整块贡献
黄色为零散块间贡献
Solution
设f(l,r)为第l到第r个块之间的逆序对个数
设g(l,r)为第l个块中任选一个数x,第r个块中任选一个数y,
如果x>y则ans++
即第l个块与第r个块可以造成的贡献
差分,可得f(l,r)=f(l+1,r)+f(l,r-1)-f(l+1,r-1)+g(l,r)
g(l,r)即对于l中每个数查询r中大于其的数个数
这个可以归并实现
这部分总复杂度O( sqrt(n) * sqrt(n) * sqrt(n) ) = O( nsqrt(n) )
Solution
Solution
零散块对整块的贡献可以差分
即预处理出零散块对前i个整块的贡献
于是对[l,r]这些整块的贡献即pre[r] - pre[l-1]
考虑到零散块最多只有O( n )种
整块有O( sqrt(n) )个
于是复杂度O( (n+m)sqrt( n ) )
Solution
零散块对零散块的贡献可以归并得到
O( sqrt( n ) )
总复杂度O( nsqrt( n ) + msqrt( n ) )
常数较大
经典问题
强制在线,序列,多次查询一个区间[l,r]内
最小的|ai-aj| , l <= i , j <= r
Solution
还是用刚刚的方法
可以O( nsqrt( n ) )预处理出块内的答案
考虑一个零散块会和哪些块有贡献
必然是从其前面那个块开始的一个后缀
Solution
于是可能的零散块-整块贡献只有nsqrt( n )种
对于每个零散块维护一个后缀min即可
零散块和零散块的贡献还是归并得到
O( (n+m)sqrt( n ) )
多区间合并
给定一个序列,多次查询区间幺半群信息
幺半群可以粗略认为是可以O(1)合并,不能差分的信息
预处理复杂度:O( n * f(n,k) ),查询的时候合并k次,k+1个区间
k=0:f(n,0)=n
k=1:f(n,1)=logn,所谓的“猫树”
k=2:f(n,2)=loglogn,所谓的“sqrt-tree”
k=3,4:f(n,3)=f(n,4)=log*n
…
k=α(n):f(n,α(n))=α(n)
根号分治
根号分治
一个不怎么好的抽象:
有n个数和为m,则最多有m/a个数大于a
剩下的数都不大于a
如果对于每个大于a的数我们可以O(x)维护
那我们就以O( xa )的额外复杂度保证了这些数都<=a
经典问题
给一张n个节点m条边的无向图
n,m,q<=1e5
1.把x点权加y
2.查询x相邻的点权和
Solution
图中每个点的度数和是m
我们可以对这个度数进行根号分治
度数>=sqrt(m)的点最多只有sqrt(m)个
度数
对每个度数>=sqrt(m)的点维护答案
每次修改
枚举所有度数>=sqrt(m)的点,如果和修改点相邻,则更新答案
每次查询
如果这个点度数>=sqrt(m),直接输出维护的答案
如果这个点度数
经典问题
序列a,每次给个x和y
查询最小的|i-j|
使得ai==x,aj==y
Solution
对于颜色进行根号分治
出现次数大于sqrt(n)的颜色只有sqrt(n)种
预处理这些颜色到每个颜色的答案
这一步是O( sqrt(n) * n ) = O( nsqrt(n) )的
Solution
这样如果查询的x和y
其中有一个是出现次数大的颜色
我们可以O(1)得到答案
如果没有呢?
Solution
如果没有,那最多有各sqrt(n)个位置值为x,y
可以进行归并排序来维护答案
这部分复杂度为O( msqrt(n) )
总复杂度O( nsqrt(n) + msqrt(n) )
IOI2009 Regions
N个节点的树,有R种属性,每个点属于一种属性。
有Q次询问,每次询问r1,r2,回答有多少对(e1,e2)满足e1属性是r1,e2属性是r2,e1是e2的祖先。
Solution
把询问离线一下(为了线性空间)
还是对颜色进行根号分治
推推式子即可
SHOI2006 Homework
1 X : 在集合 S 中加入一个X,保证 X 在当前集合中不存在。
2 Y : 在当前的集合中询问所有X mod Y最小的值
X,Y <= 1e5
Solution
考虑根号分治
对于sqrtn以内的Y,每次修改即更新所有这个的答案
对于sqrtn以上的Y,即需要支持:
O( sqrtn )修改,O( 1 )查询前驱后继
我们对值域分块
每个块中位置维护出
1.块内其前面最近的X
2.如果块内其前面没有X,则维护出其最近的有X的块
Solution
修改的时候,我们修改X所在块内的1
然后枚举每个后缀的块,将其2对这个块取max
同时维护块内最后的一个X
查询时,如果当前查询的kY在块内有1的答案,则使用
否则使用其2的答案的块的最后的一个X
总时间复杂度O(msqrtv)
POI2015 Odwiedziny
树,点权,多次查询,每次给x,y,k
求从x开始,每次跳过k个节点跳到y,所经过节点的和
保证跳到y
Brute
考虑对k根号分治
如果k <= sqrt(n),可以将询问离线,对每个k=1...sqrt(n)都跑一遍
如果k > sqrt(n),最多跳上sqrt(n)次
k <= sqrt(n)时单次可以做到O(n)
k > sqrt(n)时用倍增/树链剖分求k祖先,单次O( logn )
总复杂度O( nsqrt(n) + msqrt(n)logn )
简单根号平衡后达到O( msqrt(nlogn) )
Improved Algorithm
可以用O(1) k祖先的方法来实现
预处理可以写O( nsqrt(n) )的,这样查询常数较小
或者可以用树链剖分,边跑边找出这个重链上所有该算进去的点
O( sqrt(n) + logn )
[Ynoi2015]いまこの時の輝きを
查询一个区间乘积的约数个数
mod 19260817
值域v<=1e9
Brute
一个数的约数个数
即为:
Pi为i出现次数
对于每个数,质因子的个数只有logv个
(我不会打公式)
Brute
可以莫队暴力维护区间的这个东西
每次转移O( logv )
总复杂度O( nsqrt(m)logv )
TLE
Improved Brute
考虑到一个数本质不同的约数个数并没有logv个
最坏的情况是2*3*5*7...这样
其实这个的个数是O( logv/loglogv )
还是莫队转移
O( nsqrt(m)logv/loglogv )
TLE
Solution
可以用根号分治优化复杂度
一个数大于v^1/3的质因数只有2个
小于等于v^1/3的质数只有v^{1/3}/logv个
当v=1e9时,小于1000的质数只有168个
Solution
跑莫队的时候只维护大于v^1/3的质数的贡献
这一部分是O( nsqrt(m) )的
小于等于v^1/3的质数,每个开一个前缀和,就可以O(1)知道其在区间中出现次数
这一部分是O( m v^{1/3} /logv )的
然后对于每个数分解质因数是O( n v^1/4 )的
总复杂度O( n(v^{1/4}) + m(v^{1/3})/logv + nsqrt(m) )
根号重构
根号重构
本质为时间分块
假设:
可以O(x)重构整个序列
可以O(y)算出一个修改操作对一次查询的影响
如果每隔t个修改重构整个序列
则复杂度为O( tx )+O( m^2/ty )
经典问题
带link cut树上路径kth
(基于树分块也可以同复杂度维护,这里讲根号重构的做法)
Solution
根号重构,每过sqrtm次重构一次
这样一次操作会转换为查询sqrtm段上次重构后的树链的kth
用可持久化Trie维护,在这sqrtm个Trie上一起二分
每次查询复杂度O( sqrtmlogn )
每次重构复杂度O( nlogn )
总复杂度O( msqrtmlogn + nsqrtmlogn ) = O( (n+m)sqrtmlogn )
树上分块
Topology cluster partition
真实的树分块——Topology Cluster Partition
树分块将 n 个结点的树分成了一些块的并,满足下列性质:
1.每个块是树
2.每个块中有两个特殊的点,称为端点 1 和端点 2。
3.不同块的边集不相交
4.一个块中的顶点,除端点外,其余顶点不在其它块中出现
5.如果一个顶点在多个块中出现,那么它一定是某一个块的端点 2,同时是其余包含这个顶点的块的端点 1
6.如果把所有块的端点作为点,每块的端点 1 和端点 2 连有向边,则得到一棵有根树
Topology cluster partition
怎么求出来呢?
可以发现这个cluster和top tree的cluster是一样的,所以我们把原树的top tree建出来,然后从中提取O( sqrt( n ) )所对应的那一层即可,时间复杂度O( nlogn )
有没有简单一点的做法?
Topology cluster partition
这里给出树分块的一个实现,满足块数和每块大小均为 O( sqrtn ):
在有根树中,每次选一个顶点 x,它的子树大小超过sqrtn,但每个孩子的子树大小不超过sqrtn, 把 x 的孩子分成尽可能少的块(以 x 为端点 1,但暂时允许有多个端点 2,且每块至多有 2sqrtn 个顶点),然后删掉 x 的子树中除 x 外的部分。
重复直到剩下的点数不超过sqrtn,自成一块。
这样就求出一个保证块中顶点数和块数均为 O( sqrtn )的树分块(块间可以共用一些顶点,但每条边只属于一个块),如果一个块有多个端点(即被多个块共用的点),则在块内将这些端点 建出虚树,将虚树上的每条边细分为一个新的块,以保证最终每个块只有两个端点。
树分块
不过一般我们树分块可以更简单一些,因为一般只需要查链信息
随机撒O( sqrtn )个点,期望复杂度是正确的
COT
Solution
进行树分块,预处理任意两个关键点之间有多少种颜色
每次查询的时候一直往上跑,找到最近的关键点,得到整块的答案
Solution
对于零散部分的贡献,即需要查询这个颜色是否在一条链上出现过
可以考虑使用O( sqrtn )修改,O( 1 )查询的可持久化树上前缀和,其实就是一个可持久化数组
于是可以计算零散部分贡献,每次查询的时候零散部分共O( sqrtn )个点
这样时间复杂度O( msqrtn ),空间复杂度O( nsqrtn ),(空间复杂度其实是O( n^(1+eps) ))
简单的例题
[Ynoi2010]D1T2
序列
1.区间染色
2.区间选出两个数相等的方案数
Solution
这题不弱于小Z的袜子,而小Z的袜子双向规约矩阵乘法,故难以polylog解决
考虑分块
大概的思想
使用一个数组A[i][j]来表示第i个块对第j个块的答案
这里表示的意思是从第i个块中选出一个数,第j个块中选出一个数,相等的方案数
Solution
先对原序列分块
考虑区间染色的颜色段均摊,对块进行分类
不妨设询问数和序列长度均为B^2;(可以理解为B=sqrtn)
将序列分为B块,每块大小为B;
每个块有两个状态:
状态1:块由一些段组成,每段内颜色相同
状态2:整个块只有一种颜色
题解
在状态1表示的块中,维护一个序列表示依次出现的段的颜色、长度
在状态2表示的块中,维护块的颜色
Solution
记A(x,y),x
记t[x,y]表示块x中颜色y的元素个数,以t[1..x,y]的和的形式记录。
Solution
接下来考虑几个基本操作:
(a).在状态1表示下,块x中颜色y的元素个数增加了z;
A[x,x']+=t[x',y]*z
B[x]+=t[x,y]*z+z*(z-1)/2
t[x,y]+=z
复杂度:由于枚举 x’,所以复杂度是O( B )的
Solution
(b).将一个块x染色为y,并变为状态2表示;
如果x在状态1,使用不超过B次(a)将块内所有颜色清空;
将x设为状态2,并记录颜色为y,修改B数组。
(c).将一个块x从状态2表示变为状态1表示;
使用一次(a)即可。
Solution
用基本操作可以组合出题目需要的预处理,修改和查询:
(1).预处理
可以将每个块初始置为空,转为不超过B^2次区间染色。
Solution
(2).区间染色
区间染色需要在区间端点所在的块进行(a)(c)操作并维护段的情况,在完整块进行(b)操作;
由于每次区间染色只增加O(1)段,操作(a)的次数是均摊O(1)的。
操作(b)(c)除去调用(a)的情况,时间复杂度为O(1)。
每次(a)操作涉及到A1[x,*],A2[*,x],t[x,y]的修改,修改后重新计算前缀和,时间复杂度为O(B)。
Solution
(3).区间查询
对于类型1的完整块之间的贡献,需要查A的矩形和(转为A中O(B)次区间和,差分可得),以及B的区间和;
统计零散部分和类型2的块中,查出每种颜色的出现次数,并查询t数组的区间和,这里我们对t数组建一个前缀和可以答案都查询复杂度单次O(1),即维护块前缀和,可以得到其余的贡献。
综上,时空复杂度均为O(B^3)。
[Ynoi2011]D1T1
序列
1 x y z : a[y] , a[y+x] , … a[y + kx] += z,这里y + (k+1)x > n,且y < x
2 l r : a[l] + a[l+1] + … + a[r]的和
Solution
若x n ,则我们暴力给每个位置加,需要加的次数为O( sqrtn )次。由于需要查询区间和,用分块维护,总修改、查询复杂度为O( msqrtn )。
若x < sqrtn ,我们需要用另外的方法维护。
注意到单次修改是针对整个序列的元素,所以对x,y相同的修改,我们可以累加它的贡献。
Solution
我们对每个x,维护y的前缀、后缀和。对于一次询问,我们可以当成把序列分成了若干个大小为x的块。
中间的整块元素,每个块里肯定所有的y都有,增加的贡献就是关于x的修改总和。所有块的贡献相同,可以O(1) 算。
边角的话,由于我们记录了前缀、后缀和,也可以O(1) 算。两个端点在同一个块中,则直接前缀和相减即可。
总时间复杂度 O( msqrtn )
[Ynoi2011]D2T2
给你一个长为 n 的序列,有 m 次查询操作。
每次查询操作给定参数 l,r,b,需输出最大的 x,使得存在一个 a,满足 0≤a
Solution
考虑对b的大小进行根号分治
对较大的b,我们考虑莫队维护出区间的bitset A
然后把这个bitset每b个为一组
初始是一个大小为b的,全1的bitset B
然后每次and上我们目前A最前b位,然后A >>= b
这样当我们B == 0时,相当于找到答案了
时间复杂度O( nsqrtm + nm/b + nm/w )
Solution
对于比较小的b,可以对每个b跑一次莫队,这里分别维护b个bitset,第x个bitset表示mod b=x的元素
每次对这b个bitset找第一个0即可
这部分的时间复杂度为O( nsqrt(bm) + nm/w )
总时间复杂度O( nm/w )
CodeForces 840E. In a Trap
一棵树,点有点权ai,每次查询u到v路径上的max(ai xor dis(i,v)),保证u是v的祖先。
值域是[0,65536]
Solution
注意到值域很小,从这里入手,由于题太多讲不完就留作作业吧
[Ynoi2012]D2T2
给你一棵边权为 1,且以 1 为根的有根树,每个点有初始为0的点权值,定义两个点的距离为其在树上构成的简单路径的长度,需要支持两种操作:
1 a x y z:把 a 子树中所有与 a 的距离模 x 等于 y 的节点权值加 z。
2 a:查询 a节点的权值。
2019 Multi-University Training Contest 8 G
Solution
这个问题的形式目前我并不会polylog,于是考虑根号分治
考虑对于每次修改,如果x大该如何维护
可以对原树按照深度分层,每层的节点按照在原树的DFS序上的位置排序,转换为在n / x层上区间加
需要O( 1 )进行区间加,和找出每层在哪个区间进行区间加
前者平凡,使用一个O( 1 )区间加O( sqrtn )查询单点的分块即可,后者需要一些技巧性的方法
Solution
可以根号重构,每次对原树进行长链剖分,维护合并上来的每个节点每个深度的DFS序最小位置和DFS序最大位置
我采用了一个更好的做法:
记每个节点的深度为dep,DFS序上所对应的区间左端点为l,右端点为r,自己在DFS序上的位置为l
建立两个新的森林F1,F2
F1中x向y连边当且仅当dep[y] = dep[x] + 1 , l[x] < l[y] , 且l[y]最小
F2中x向y连边当且仅当dep[y] = dep[x] + 1 , l[x] > r[y] , 且r[y]最小
Solution
可以证明一个节点a在F1上的k层祖先即为节点a在原树子树中深度比其大k的所有节点里面DFS序最小的节点,在F2上的k层祖先即为节点a在原树子树中深度比其大k的所有节点里面DFS序最大的节点
于是我们可以通过在这两个森林中找k祖先来找到我们需要加的区间,这里可以每次批量找n / x个区间的端点,O( logn + n / x )在轻重链剖分结构上找出即可
于是可以O( sqrtn + n / x )解决
Solution
考虑对于每次修改,如果x小该如何维护
可以对每个x,将原树按照深度mod x进行分层,每次查询的节点对于每个x只会出现在一层中,于是需要查询x次
对于每个x,对于每个0...x-1的余数,将其按照DFS序排序,这里按照DFS序枚举就可以O( n )达成,子树修改即变成区间加
这样可以使用一个O( sqrtn )区间加O( 1 )查询单点的分块维护,这里区间的左右端点可以二分得到
于是可以一次O( nx )的预处理加上单次复杂度O( sqrtn + x )解决
在x=sqrtn处进行根号分治,即总时间复杂度O( (n + m)sqrtn ),空间复杂度O( n + m )
Hdu 6615
There is a tree with vertex 1 as a root. All vertices of the tree are colored.
Your task is to determine the number of sub-trees with exactly k distinct colors.
There are two types of queries.
1 u c : paint vertex u with color c.
2 k : answer the query.
2019 Multi-University Training Contest 4
Solution
每个点维护子树颜色个数
将x位置颜色从y改到z
对每个颜色维护子树中其出现的次数
每次修改一个位置的颜色则相当于O(1)次链+1-1的操作
相当于链+1-1,全局x出现次数
Solution
这个形式强于区间+1-1区间0个数,这个我们目前认为难以polylog解决,考虑分块
对原树进行树分块,维护簇路径的值域数组,表示簇路径上每个值出现次数
然后对簇路径的操作可以O(1)完成,又只有O( sqrtn )个零散的点
总时间复杂度O( msqrtn ),空间复杂度可以做到O( n + m )
[Ynoi2013]D1T2
Solution
对原序列建一棵线段树,考虑怎么在线段树上面修改和查询
定义 极长 “X” 段为一个极长的子区间,使得区间中符号均为乘法
区间值修改
回忆起前面一个莫队题的性质,这道题中同样存在:
维护出区间中每个极长的 “X” 段的长度,可以发现这个存在一个自然根号:
假设区间长度为size,则最多只有O( sqrt( size ) )种极长 “X” 段的长度
每次对区间进行值修改的时候,即对这个长度为O( sqrt( size ) )的多项式进行插值,暴力计算即可,插值复杂度为O( sqrt( size ) ),即可以O( sqrt( size ) )的时间将一个节点值进行修改,同时维护信息
区间符号修改
每次对区间符号进行修改的时候,区间的信息只会变成区间和或者区间乘积,所以我们每个节点要维护区间和和区间乘积
符号修改之后,这个节点的极长 “X” 段只会有O( 1 )种了
符号进行修改可能影响一些节点的极长 “X” 段,考虑如何维护这个
区间符号修改
对一个节点,我们可以归并两个儿子的极长 “X” 段,来维护出这个节点的极长 “X” 段
对一个大小为size的节点进行归并,代价是O( sqrt( size ) )的
注意需要特判左儿子的最右极长 “X” 段是否和右儿子的最左极长 “X” 段进行合并
区间信息合并
合并区间信息的时候,只需要把左右儿子信息加起来,同时特判O(1)个位置即可
这O(1)个位置就是左儿子的最右部分和右儿子的最左部分
可以处理:
标记对标记的影响
标记对信息的影响
信息和信息的合并
所以我们正确性有保证了
Complexity
我们所有地方的复杂度都是O( sqrt( size ) )的
线段树在每层只会递归到2=O(1)个节点中,所以每层只有O(1)个节点的信息需要更新
Complexity
T( n ) = T( n / 2 ) + O( sqrtn )
sqrt( n ) + sqrt( n /2 ) + sqrt( n / 4 ) + … + sqrt( 1 ) = O( sqrtn )
空间:
T( n ) = 2T( n / 2 ) + O( sqrtn )
sqrt( n ) + 2sqrt( n / 2 ) + 4sqrt( n / 4 ) + … + nsqrt( 1 ) = O( n )
总时间复杂度O( msqrtn ),空间复杂度O( n )
CF700D Huffman Coding on Segment 3100
给一个长为n的串,有q次询问,每次询问一个区间的最小二进制编码长度,即在可以唯一还原的前提下,将这一段子串转化为长度最小的二进制编码。
Solution
哈夫曼编码就是把每个出现过的元素提出来,按照出现次数加权,做合并果子
哈夫曼树在排序后可以做到线性
维护两个队列,第一个是初始的所有排好序的元素,第二个保存合成的所有元素,初始为空
每次从每个队列中选前2大的元素,找最小的两个合成,合成后放入第二个队列末端
Solution
有一个性质是不同的出现次数是O(sqrtn)的,考虑1+2+…+n=n(n+1)/2
考虑使用莫队维护出区间每个数的出现次数,从小到大排序
这个有多种维护方法,我之前写过的方法是记录下莫队转移时所有变化,然后到一个查询区间时一起处理掉,用莫队上一个处理的询问维护的区间不同的出现次数,以及记录的转移,得到这个区间的所有出现次数
时间复杂度O(nsqrtm+msqrtn)
Solution
这里考虑可以批处理同一个出现次数出现很多次的情况
如果当前最小是相同的x个a,则可以合并出x/2个2a
我们边维护两个队列边缩点
复杂度分析:
每O(1)次合并,下一次可能合并出的元素大小至少变大1
经过O(sqrtn)次合并,只可能合并出>sqrtn的元素了
而这两个队列如果均>sqrtn,则有O(sqrtn)个元素
每次合并减少一个元素,此时合并O(sqrtn)次
时间复杂度O(nsqrtm+msqrtn)
[Ynoi2013]D2T2
给一个长为 n 的序列,有 m 次查询操作。
查询操作形如 l r L R,表示将序列中值在 [L,R] 内的位置保留不变,其他的位置变成 0 时,序列中 [l,r] 区间内的最大子段和,这个子段可以是空的。
Solution
先研究全局查询的情况,考虑离散化后所有值域区间对应的不同的序列只有O( n^2 )种,我们可以分治来维护两边的最大前缀和,最大后缀和,最大子段和。
合并的时候,左儿子有个答案矩阵,右儿子也有个同规模的答案矩阵,我们把这两个稀疏化一下(大概就是说你每次把块内存在的值归并上来,这个矩阵会变大常数倍),然后就可以合并了,每次合并的是O( n^2 )的
所以这里我们有T( n ) = 2T( n / 2 ) + O( n ^ 2 ),解得T( n ) = O( n ^ 2 )
Solution
我们先在外层对序列分块,这样有O( sqrtn )个O( sqrtn )大小的块,每个块的分治预处理代价是T( sqrtn ) = O( n )的,所以预处理的总复杂度是O( sqrtn ) * O( n ) = O( nsqrtn )的
我们对序列每个块逐个处理,然后每次合并出答案即可
时间复杂度O( (n + m)sqrtn ),空间复杂度O( n + m )
[Ynoi2014]空の上の森の中の
线段树是一种特殊的二叉树,满足以下性质:
每个点和一个区间对应,且有一个整数权值;
根节点对应的区间是 [1,n];
如果一个点对应的区间是 [l,r],且 l
珂朵莉需要维护一棵线段树,叶子的权值初始为 0,接下来会进行 m 次操作:
操作 1:给出 l,r,a,对每个 x 将 [x,x] 对应的叶子的权值加上 a,非叶节点的权值相应变化;
操作 2:给出 l,r,a,询问有多少个线段树上的点,满足这个点对应的区间被 [l,r] 包含,且权值小于等于 a。
Solution
可以证明这个线段树只有O( logn )种不同大小的节点
对于每种节点大小分层,维护一个数据结构,支持:
1.区间加
2.单点修改
3.区间rank
这个是一个经典问题,目前上界是O( msqrtn ) ,我们通过一些规约证明了这个问题不弱于一个 sqrtn*sqrtn 的矩阵乘法,所以目前认为难以达到O( n*polylogn ) 的复杂度
Solution
可以证明线段树的每层只有O(1) 种不同大小的节点,那么我们的总时间复杂度是
O( msqrtn + msqrt(n/2) + msqrt(n/4) + … ) = O( msqrtn )
空间复杂度可以通过一些trick做到O( n + m )
[Ynoi2016]D1T1掉进兔子洞
有 m 个询问,每次询问三个区间[l1,r1] [l2,r2] [l3,r3]
记f( x , l , r ) 表示区间 [l,r] 中x的出现次数
查询:sum( i = 1 to n ) min( f( i , l1 , r1 ) , f( i , l2 , r2 ) , f( i , l3 , r3 ) )
Brute
先考虑如果每个数不相同怎么做
莫队跑出每个区间的值域bitset,然后&起来,这些就是被删掉的数了
Solution
想办法转换一下
先离散化,假设数x离散化后的位置是y,然后x出现z次
那么y,y+1…y+z-1这些位置都是x的
莫队维护区间bitset的时候
假设区间中y出现了w次
则我们把y,y+1…y+w-1这些位置填上1
y+w…y+z-1这些位置填上0
Solution
用这样处理过的bitset,&起来
&后得到的bitset里面的1的个数就是删掉的所有数了
总复杂度O( nsqrt(m) + nm/w ) = O( nm/w )
Note
这里为了方便,每次只给了三个区间,所以理论上来说可以跑一个6维的莫队,但我可以每次给任意k个区间,这样的算法复杂度就会变成O( n^(2-eps) )
[Ynoi2017]D1T1由乃的玉米田
序列,每次给参数l r c
查区间[l,r]是否可以选出两个数a,b使得:
a+b=c
a-b=c
a*b=c
a/b=c
值域1e5
除法是整除,也就是说 3/2 这种情况下认为二者不能除
Solution
Solution
Solution
假设新的右端点是r,上面的值是x
则对于每个x的的约数y,y最近一次出现的位置l到现在的右端点位置r
包含[l,r]这个区间所有区间都可以选出(x,y)这一对数使得其比利为x/y
于是我们根据这个扫描线即可,要扫两遍
复杂度是c的约数个数
Solution
对于-操作
维护区间的值域上的bitset
每次如果bitset & ( bitset << c )后不是0
则找到两个数a,b使得a-b=c
本质为用bitset优化了bool数组的匹配
然后就可以莫队维护区间的值域bitset了
加操作维护一个反的bitset即可
Solution
+的复杂度:O( nsqrt(m) + vm/w )
-的复杂度:O( nsqrt(m) + vm/w )
*的复杂度:O()
/的复杂度:O()
存在理论复杂度更优的做法,但是常数较大而not practical
矩阵乘法相关规约
Why
为什么这些题我们要用分块来处理?不能分治吗
Reason
很多分块题是不弱于sqrtn*sqrtn大小的矩阵乘法的
由于目前矩阵乘法上界只做到了O( n^2.373 ),所以目前技术做这些分块题无法低于O( n^(1+x) ),x is const,x > 0
目前有规约的问题
小Z的袜子(区间每个数出现次数平方和):双向规约01矩阵乘法,已经低于了O(n^1.5)
区间逆序对:双向规约01矩阵乘法,已经低于了O(n^1.5)
区间众数:单向规约布尔矩阵乘法,已经低于了O(n^1.5)
链颜色数:单向规约01矩阵乘法
目前有规约的问题
区间出现次数奇数次的数个数:单向规约01矩阵乘法
区间最大的|i-j|满足ai==aj:单向规约max-plus矩阵乘法(好像是)
区间加,区间小于x的数个数:单向规约01矩阵乘法
区间加,区间kth :单向规约01矩阵乘法
例子
假设给你一个黑箱,可以解决链颜色数问题,如何用这个黑箱来解决01矩阵乘法?
指Ans[i][j] = sum_k A[i][k] * B[k][j],值是[0,1]中的整数
规约
我们可以构造一棵:
根有sqrtn叉,下面接了sqrtn条链的树,总共sqrtn种权值
每次选出前sqrtn/2条链,和后sqrtn/2条链,总共有O( n )种不同的询问,询问这些链的并的颜色数
记:
A[i][j]表示第i条链是否有第j种颜色,这里i
规约
可以发现我们的询问即
Ans[i][j] = sum_k A[i][k] | B[j][k]
令C = B^T
则
Ans[i][j] = sum_k A[i][k] | C[k][j]
规约
由于值域是01,所以&和*等价,把每个数取反之后|就变成&了
所以
Ans[i][j] = sum_k A[i][k] * C[k][j]
我们通过这个黑箱实现了sqrtn*sqrtn 01矩阵的矩阵乘法
注意到这里规约是单向的,也就是说我们无法依靠快速矩阵乘法来得到低于O( n^1.5 )的链颜色数算法
大分块
目前最复杂的根号数据结构题
[Ynoi2018]未来日记
最初分块
2017 Multi-University Training Contest 4 M
给你一个序列
1.区间所有x变成y
2.区间kth
[Ynoi2018]未来日记
对这题的评价:8-9/11
Solution
先考虑如何求区间第k小值。对序列和权值都进行分块,设bi,j表示前j块中权值在i块内的数字个数,ci,j表示前j块中数字i的出现次数。那么对于一个询问[l,r],首先将零碎部分的贡献加入到临时值域分块数组tb和tc中,然后枚举答案位于哪一块,确定位于哪一块之后再暴力枚举答案即可在O( sqrtn )的时间内求出区间第k小值。
这个做法类似于在可持久化Trie上一起二分来查询区间kth,不过是在分块结构上一起跑来进行查询。
Solution
接着考虑如何实现区间[l,r]内x变成y的功能。显然对于零碎的两块,可以直接暴力重构整块。对于中间的每个整块,如果某一块不含x,那么无视这一块;否则如果这一块不含y,那么只需要将x映射成y;否则这一块既有x又有y,这意味着x与y之间发生了合并,不妨直接暴力重构整块。因为有c数组,我们可以在O(1)的时间内知道某一块是否有某个数。
Solution
考虑什么情况下会发生重构,也就是一个块内发生了一次合并的时候。一开始长度为n的序列会提供O(n)次合并的机会,而每次修改会对零碎的两块各提供一次机会,故总合并次数不超过O(n+m),而每次合并的复杂度是O( sqrtn )的,因此当发生合并时直接重构并不会影响复杂度。
Solution
那么现在每块中的转换情况只可能是一条条互不相交的链,只需要记录每个初值转换后是什么,以及每个现值对应哪个初值即可。遇到查询的时候,我们需要知道零碎部分每个位置的值,不妨直接重构那两块,然后遍历一遍原数组a即可得到每个位置的值。
在修改的时候,还需要同步维护b和c数组,因为只涉及两个权值,因此暴力修改j这一维也是可以承受的。
总时间复杂度O( (n+m)sqrtn ),空间复杂度O( nsqrtn )
Solution
这题主要的思路就是通过对序列和权值一起进行分块,然后让序列分块的O( sqrtn )部分乘上值域分块的O( 1 )部分,序列分块的O( 1 )部分乘上值域分块的O( sqrtn )部分,从而达到了复杂度的平衡。
[Ynoi2018]五彩斑斓的世界
第二分块
Codeforces 897 E
1 l r x : 把区间[l,r]所有大于x的数减去x
2 l r p : 查询区间[l,r]内的x的出现次数
值域1e5
[Ynoi2018]五彩斑斓的世界
对这题的评价:6/11
Solution
这个值域1e5很明显复杂度和值域有关
Solution
考虑分块,可以发现每块的最大值总是不增的
总的所有块的最大值和当块大小为O( sqrt(n) )时为O( nsqrt(n) )
(假设值域和n同阶)
考虑怎么利用这个性质
Solution
可以发现:假设区间所有大于x的减x,最大值为v
这个操作等价于把区间中所有数减x,之后小于0的再加x
当v >= x * 2时,可以把所有[1,x]内的数合并到[x+1,x*2]上
当v < x * 2时,可以把所有[x+1,v]内的数合并到[1,v-x]上
Complexity
如果v >= x * 2
我们用O( x ) * O( 数据结构复杂度 ) 的代价使得块内的最大值减少了O( x )
如果v < x * 2
我们用O( v - x ) * O( 数据结构复杂度 )的代价使得块内的最大值减少了O( v - x )
Solution
所以要用一个数据结构支持:
O( 1 )把块内值为x的全部变成x+v或者x-v
O( sqrt(n) )求出块内经过大量操作后,每个数的值
第一种是整块操作的时候要用
第二种是重构零散块的时候要用
Solution1
维护这个有很多种方法
可以每块维护一个值域上的链表
定义f[i][j]为第i块里面所有值为j的数的下标的链表
区间所有x变成x+v即link( x , x + v )
然后维护一下块内可能出现的所有数
每次重构的时候即遍历所有可能出现的数,然后遍历其中真正出现的数的链表即可
Solution1
不过链表常数巨大。。。
这个应该跑的很慢
Solution2
可以每块每个值维护一个vector
然后启发式合并这个vector
这个做法由于对缓存友好,所以会跑的快一些
Solution3
可以用一个并查集维护
这个并查集由于只支持:
1. merge( x , y )
2. for( i = 1 ; i <= sqrtn ; i++ ) find( i )
所以复杂度是O( 1 )的并查集
本质上和链表的做法是差不多的,不过常数好很多
时间复杂度O( (n+m)sqrtn ),空间复杂度O( nsqrtn )
[Ynoi2019]Another
[前]第三分块
树,每个点有编号
1.改一条边的边权
2.查询一个点到一个编号区间[l,r]的点的距离和
[Ynoi2019]Another
对这题的评价:5/11
Solution
对点的编号序列分块
考虑维护f(j,i)表示dfs序为i的点到前j个块的距离和
修改一条边的边权的时候,看造成什么样的影响:
Solution
只可能是红色的点和绿色的点之间互相影响
枚举前i块,可以O( 1 )知道第i块里面有多少在红色的部分里面,设这个为x
于是对dfs序在绿色部分的所有i,把f(j,i)加上x*修改的v,相当于我们要对f再做一个O( 1 )修改O( sqrtn )查询的分块结构
Solution
查询的时候,我们要查点i到[l,r]的贡献,就找离l和r分别最近的两个块端点,然后O( sqrtn )查出i到这两个前缀块的答案,然后把这两个差分一下
于是我们解决了整块的答案,考虑怎么查询零散
Solution
零散部分每次有O( sqrtn )个两点间距离和
然后现在考虑怎么快速查两个点之间的距离和
dist(i,j) = dep[i] + dep[j] – 2 * dep[ lca(i,j) ]
每次改变边权,相当于对dfs序的一段进行区间加,于是我们对dfs序再次分块,实现一个O( sqrtn )区间加,O( 1 )查单点的平衡
使用O( 1 )lca的话,我们就可以O( 1 )计算两点之间的dist了
于是问题得到解决
时间复杂度O( (n+m)sqrtn ),空间复杂度O( nsqrtn )
[Ynoi2018]天降之物
第四分块
51nod 算法马拉松35
序列a
1.把所有x变成y
2.查询最小的|i-j|使得ai==x,aj==y
[Ynoi2018]天降之物
对这题的评价:5/11
Solution
考虑根号分治
定义一个值x出现次数为size[x]
如果没有修改操作,则预处理所有size大于sqrtn的值到所有其他值的答案,以及每个值出现位置的一个排序后的数组
查询的时候如果x和y中有一个是size大于sqrtn的,则可以直接查询预处理的信息,否则进行归并
O( nsqrtn + msqrtn )
Solution
有修改操作即在这个做法上改良,因为发现这个做法的根号平衡并没有卡满,所以有改良余地
假设把所有x变成y
由于可以用一些技巧使得x变成y等价于y变成x,所以不妨设size[x] < size[y]
定义size大于sqrtn为大,size小于等于sqrtn为小
定义ans[x][y]为x到y去除附属集合的部分的答案(附属集合是什么下面有说)
x取遍所有值,y只有所有大的值,总O( sqrtn )个
Solution
修改:
如果x和y均为大,则可以暴力重构,O( n )处理出y这个值对每个其他值的答案,因为这样的重构最多进行O( sqrtn )次,所以这部分复杂度为O( nsqrtn )
如果x和y均为小,则可以直接归并两个值的位置的排序后的数组,单次O( sqrtn ),所以这部分复杂度为O( msqrtn )
如果x为小,y为大,发现小合并进大的均摊位置数为O( n ),对这个再次进行根号平衡
对于每个大,维护一个附属的位置集合,这个位置集合的大小不超过sqrtn
每次把小的x合并入大的y的时候,即合并入这个附属集合,并且用x到所有大的值的答案更新y到所有大的值的答案,这样
如果合并后附属集合大小超过sqrtn,则O( n )重构y到所有值的答案,这个过程最多进行O( sqrtn )次,均摊复杂度O( nsqrtn )
由于大的值个数 <= sqrtn , 附属集合大小 <= sqrtn,这一部分是单次O( sqrtn )的,所以这部分复杂度为O( msqrtn )
Solution
查询:
如果x和y均为大,则在维护的答案中查询min( ans[x][y] , ans[y][x] ),然后将x的附属集合和y的附属集合进行归并,这一部分是单次O( sqrtn )的,所以这部分复杂度为O( msqrtn )
如果x和y均为小,则进行一次归并即可,所以这部分复杂度为O( msqrtn )
如果x为小,y为大,则在维护的答案中查询ans[x][y],然后将x和y的附属集合进行归并,这一部分是单次O( sqrtn )的,所以这部分复杂度为O( msqrtn )
由于维护了所有可能的贡献,而且更新是取min,正确性也得到了保障
时间复杂度O( (n+m)sqrtn ),空间复杂度O( nsqrtn )
Solution
存在序列分块的做法
[Ynoi ]
第五分块
未知
[Ynoi2018]末日时在做什么?有没有空?可以来拯救吗?
第六分块
序列
1.区间加任意数,在[-2^(w-1),2^(w-1)-1]内
2.查询区间最大子段和
[Ynoi2018]末日时在做什么?有没有空?可以来拯救吗?
对这题的评价:8/11
先看一个这题的弱化版
[Ynoi2015]世界で一番幸せな女の子
维护序列支持:
1.全局加
2.区间最大子段和
Solution1
由于可以加负数
设pre[x]为x时刻全局加的值
按照pre从小到大处理
这样就转换为了只加正数
Solution1
考虑分块
每块维护一下块内长为1…sqrt(n)的最大前缀,最大后缀,最大子段和
如果一个整块加了,那么这个整块块内的最大子段长度肯定是不降的
Solution1
每次查询的时候按照当前的全局加标记确定出每个块内的最大子段和
然后把跨块的询问用左边块的最大后缀和右边块的最大前缀拼起来
即可
总复杂度O( msqrt(n) + nsqrt(n) )
Solution2
这个根号太屑了,考虑polylog
Solution2
线段树维护:
每个节点的左,右,内部最大子段和的凸函数
凸函数是一个区间的半平面交,每个下标x对应的意义是这个节点被整体加了x后,该节点的左,右,内部最大子段和的值是多少
设左最大子段和是pre,右最大子段和是suf,内部最大子段和是mid
Solution2
然后建树的时候可以发现
cur -> pre[i] = max( cur -> left -> pre[i] , cur -> right -> pre[i] + cur -> left -> sum );
cur -> suf[i] = max( cur -> left -> suf[i] + cur -> right -> sum , cur -> right -> suf[i] );
cur -> mid[i] = max( cur -> left -> mid[i] , cur -> right -> mid[i] , cur -> left -> suf[i] + cur -> right -> pre[i] );
这个可以类比单点修改区间最大子段和理解
Solution2
我们来看看这个需要支持什么操作
需要支持:
1.把一个凸函数加上一个常数
2.求一个凸函数a,满足a[i] = max( b[i] , c[i] ),其中b,c为凸函数
3.求一个凸函数a,满足a[i] = b[i] + c[i],其中b,c为凸函数
Solution2
可以发现这三个性质都满足
而且可以通过归并两个儿子的凸函数来得到cur的凸函数
于是预处理复杂度O( nlogn )
每次查询的时候直接在线段树上查询区间即可
总复杂度O( (n+m)logn )
Solution
考虑把全局加区间最大子段和的做法拓展到区间加区间最大子段和:
先考虑加正数怎么做
如果朴素地来实现的话我们可以对序列进行分块,每块开一个数据结构
这样复杂度是O( (n+m)sqrt(nlogn) )的,因为整块的线段树可以均摊O( 1 )直接在根上打标记,主要是零散部分代价比较高
Solution
发现零散部分直接重构整棵线段树代价是O( slogs )的,过大
发现本题使用的线段树并不需要支持区间查询,只是一个分治结构而已
考虑每次修改的时候,对于每个被修改到的节点cur,只会有cur的一个儿子被修改
于是我们可以通过归并cur的两个儿子的凸函数信息来得到cur的新的信息,没有必要重构整棵线段树,只需要部分重构
Solution
由于归并复杂度是O( 节点大小 )的,而且每层只归并一个节点,所以零散部分修改复杂度变为了O( s + s / 2 + s / 4 + ... + 1 ) = O( s )
于是得到了一个时间复杂度均摊O( sqrtn )的算法
时间复杂度O( (n+m)sqrtn ),空间复杂度O( nlogn )
Solution
加任意数?
逐块处理
发现每次操作的零散块只有O(1)个,我们离线,然后逐个块处理,对每个块算出我们需要的信息即可,具体细节可能比较复杂
这样我们可以对每个块进行基数排序,把询问和点一起排序,让其从加任意数变成加正数
这里值域是Θ( m2^w ),由RAM的假设认为w=Θ( logn ),在这个假设下基数排序是线性的,所以我们同复杂度解决了加任意数
时间复杂度O( (n+m)sqrtn ),空间复杂度O( n + m )
[Ynoi2018]馱作
第七分块
THUPC 2019 A
无边权树
树上的一个邻域定义为到点x距离不超过y条边的点集,x称为邻域的中心,y称为邻域的半径。
给一棵n个点的树,m次询问,每次给出两个邻域,问两个邻域中各取一个点,两两点对间的距离之和 。
n,m≤100000
[Ynoi2018]馱作
对这题的评价:10/11
一些记号和定义
对于树上的顶点 a,b,顶点集 S,S1,S2,定义 d(a,b)表示顶点 a 到 b 的距离,若 a=b 则 d(a,b)=0,否则 d(a,b)是 a,b 间简单路径的边数; 另外定义
d(S,a) = d(a,S) = ∑ d(a,b)[b∈S]
d(S1,S2) = ∑ d(a,S2)[a∈S1] 。
树 T 上的一个邻域 NT(x,y)定义为到顶点 x 距离不超过 y 条边的顶点集。x 称为邻域的中心, y 称为邻域的半径。
Preknowledge
真实的树分块——Topology Cluster Partition
树分块将 n 个结点的树分成了一些块的并,满足下列性质:
1.每个块是树
2.每个块中有两个特殊的点,称为端点 1 和端点 2。
3.不同块的边集不相交
4.一个块中的顶点,除端点外,其余顶点不在其它块中出现
5.如果一个顶点在多个块中出现,那么它一定是某一个块的端点 2,同时是其余包含这个顶点的块的端点 1
6.如果把所有块的端点作为点,每块的端点 1 和端点 2 连有向边,则得到一棵有根树
Preknowledge
这里给出树分块的一个实现,满足块数和每块大小均为 O( sqrtn ):
在有根树中,每次选一个顶点 x,它的子树大小超过sqrtn,但每个孩子的子树大小不超过sqrtn, 把 x 的孩子分成尽可能少的块(以 x 为端点 1,但暂时允许有多个端点 2,且每块至多有 2sqrtn 个顶点),然后删掉 x 的子树中除 x 外的部分。重复直到剩下的点数不超过sqrtn,自成一块。 这样就求出一个保证块中顶点数和块数均为 O( sqrtn )的树分块(块间可以共用一些顶点,但每条边只属于一个块),如果一个块有多个端点(即被多个块共用的点),则在块内将这些端点 建出虚树,将虚树上的每条边细分为一个新的块,以保证最终每个块只有两个端点。
Solution1
如果只有单次询问,可以进行转化:
d(S1,S2) = ∑[d(a,c)*|S2|+d(b,c)*|S1| 2d(lca(a,b),c)][a∈S1,b∈S2],其中 c 是任意一个点。 这里我们取c为根节点,这样把两两顶点间的距离和转化为了点集内顶点的深度和以及两两顶点间 lca 的深度和:
d(S1,S2) = ∑[dep(a)*|S2|+dep(b)*|S1| 2dep(lca(a,b))][a∈S1,b∈S2]
对 lca 部分可以在 O(n)时间内求出:初始化树的边权为 0,将 S1 中的每个顶点到根的路径的边权+1,求 S2 中每个顶点到根的路径的边权和之和。
Solution1
首先进行树分块,方便起见,认为一个块包含块中除了端点 1 之外的点,这样每个点就恰好 属于一个块。 预处理每个块 B(端点为 a1,a2)中的 d(NB(ai,x),aj)(i,j=1,2),需要 O(n)时间和空间。
树 T 的一个邻域可以拆分为这个邻域和每个块的交。
对于块 B,若 x 在 B 中,则 NT(x,y)∩B=NB(x,y); 否则设 z 是 B 中距离 x 较近的端点,距离为 d,则 NT(x,y)∩B=NB(z,y-d)。
Solution1
求两个邻域间的距离和,只需考虑这两个邻域和每个块的交。求块 B1,B2 的两个邻域 n1=NB1(x1,y1)和 n2=NB2(x2,y2)间的距离和。 如果 xi 不是 Bi 的端点,则显式地求出 ni 以及 ni 到 Bi 的端点的距离和,这需要 O( sqrtn )的时间。
Solution1
当 B1≠B2 时,设 a 为 B1 中最靠近 B2 的端点,b 为 B2 中最靠近 B1 的端点,n1 和 n2 间的距离和 d(n1,n2)=d(a,b)*|n1|*|n2|+d(n1,a)*|n2|+d(n2,b)*|n1|。通过在块构成的树上 dfs,这部分可以在 O( sqrtn )时间内处理。
当 B1=B2 时,如果 x1 和 x2 都是 B1 的端点,每块每次询问这种情况出现至多 1 次,这里暂不考虑,最后再离线处理;否则每次询问这种情况只出现 O(1)次,可以 O( sqrtn )暴力处理。
Solution1
离线处理的部分,枚举每个块 B,再枚举询问(只需考虑两个邻域的中心都不在 B 中的询问) 计算贡献,有 O(n)个询问形如 d(NB(a,y1),NB(b,y2)),对
时间复杂度O( (n + m)sqrtn ),空间复杂度O( n )
Solution2
本题还存在利用静态top tree(RC分治)来简化问题的做法,但是限于问题的复杂性还是只能做到O( (n + m)sqrtn )时间复杂度
[Ynoi ]
第八分块
未知
[Ynoi ]
第九分块
未知
[Ynoi2019]魔法少女site
第十分块
序列
1 x y : x位置修改为y
2 l r x : 查询区间[l,r]有多少子区间的max <= x
[Ynoi2019]魔法少女site
对这题的评价:6/11
Solution
这是带修改不删除莫队,首先这个问题是四维的,一维时间维,一维值域维,两维序列维,考虑莫队维护( 时间 , max )的二元组,数据结构维护序列维:每次离线处理O( sqrtn )个操作。
Solution
令x递增扫描,维护一个与原序列等 的01序列,其中一个位置为1当且仅当原序列中此处的值小于等于x且在这些操作中没有修改过这个位置,支持将0变成1,查询内每个段(定义段为01序列上的极 区间,满足区间内均为1)的贡献( 度*( 度-1)/2)。
Solution
当x与某个询问的x相同时,处理这个询问,对于在这个询问前被修改过的位置,需要将0变为1,处理完这个询问后撤销操作;另外还需要将位置暂时设为0,在询问结束后恢复。为支持上述操作,对每个由1组成的段,在段的两端记录这个段的另一端的位置,在将0变成1时可以O( 1 )维护段的变化情况。
Solution
使用分块实现O( 1 )单点加O( sqrtn )查询区间和,将每个段的贡献记录在段的左端点上,在段发生改变时动态维护。为了支持将位置暂时设为0(此时需要知道这个位置当前是否为0,若非0还需要知道这个位置所在的段的左右端点),还需要支持O( sqrtn )查询一个位置左边的第一个左端点,并在段发生改变时O( 1 )更新一个位置是否是某个段的左端点,这同样可以使用分块实现。
综上所述,可以在O( n )时间内处理O( sqrtn )个操作,总的时间复杂度为O( (n + m)sqrtn )。
[Ynoi2018]GOSICK
第十四分块
序列,值域和n同阶
每次给出一个区间[l,r],查询存在多少二元组(i,j)满足l <= i , j <= r,且ai是aj倍数
[Ynoi2018]GOSICK
对这题的评价:8/11
Solution
我们考虑莫队维护,不失一般性这里只讨论莫队的四种拓展方向里面的一种
每次把区间[l,r]拓展到[l,r+1]的时候需要维护a[r+1]和[l,r]这段区间的贡献
这里利用莫队二次离线的trick:
莫队就可以抽象为nsqrtm次转移,每次查询一个序列中的位置对一个区间的贡献
这个贡献是可以差分的, 也就是说把每次转移的a[r+1]对区间[l,r]的贡献差分为a[r+1]对前缀[1,r]的贡献减去对前缀[1,l-1]的贡献
Solution
然后通过这个差分我们可以发现,我们把O( nsqrtm )次的修改降低到了O( n )次修改,因为前缀只会拓展O( n )次
于是我们每次可以较高复杂度拓展前缀和,因为插入次数变成了O( n )次
然后这 我们离线莫队的转移的时候可以做到线性空间,因为每次莫队是从一个区间转移到另一个区间:
我们记下pre[i]为i的前缀区间的答案,suf[i]为i的后缀区间的答案
Solution
不失一般性,只考虑把区间[l1,r1]拓展到区间[l1,r2]:
[l1,r1]区间的答案为红色部分的贡献,[l1,r2]区间的答案为红色部分加上绿色部分的贡献,r2的前缀贡献为所有的贡献,r1的前缀贡献为红色的贡献与前两个蓝色的贡献
于是我们可以把绿色的贡献,也就是两次询问的差量差分为pre[r2]-pre[r1]-{[1,l1-1]对[r1+1,r2]的贡献}
Solution
这里每个位置开个vector存 下就可以了,相当于说在l1-1位置push_back( pair < int , int > ( r1 + 1 , r2 ) ),然后扫描线扫到的时候直接暴力进行处理就可以了
于是我们达成了O( n + m )的空间复杂度将莫队给 次离线
现在考虑怎么算这个贡献,我们要高效计算区间[l,r]对x的贡献时
先把贡献拆开变成:[l,r]中x的倍数个数,[l,r]中x的约数个数
Solution
[l,r]中x的倍数个数:每次前缀加入一个数a[i]的时候,我们把a[i]的约数位置所对应的数组pre1的位置都++然
后查询的时候直接查pre1[x]即可得到x倍数个数
[l,r]中x的约数个数:这里考虑对x的约数进行一次根号分治
Solution
对于所有x 于sqrtn的约数,我们拓展前缀的时候维护,即每次把a[i]的倍数位置所对应的数组pre2的位置都++
然后查询的时候直接查pre2[x]即可得到x大于sqrtn的约数个数
对于所有x小于sqrtn的约数,我们考虑每次直接枚举区间[l,r]中1,2,...sqrtn的出现次数
这里可以先枚举1,2,...sqrtn,然后预处理一个前缀和,O( n + m )算出对每个询问的贡献,从而节省空间
于是我们得到了 个总时间复杂度O( n( sqrtn + sqrtm ) ),空间O( n + m )的做法
Thanks for listening
同课章节目录
