北师大版八下数学1.1等腰三角形 课件(共24张PPT)
文档属性
| 名称 | 北师大版八下数学1.1等腰三角形 课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-19 20:59:49 | ||
图片预览






文档简介
(共24张PPT)
1.1 等腰三角形
北师大版 数学八年级下册 第一章 三角形的证明
1.理解等边三角形的判别条件及其证明;并能利用定理解决一些简单的问题.
2.理解含有30 角的直角三角形性质及其证明,并能有意识渗透逆向思维的思想。
学习目标
②角: 等腰三角形的两个底角相等.
(等边对等角)
③轴对称性: 等腰三角形顶角的平分线、底边
上的中线、底边上的高线互相重合 .
1、等腰三角形的性质:
①从边来判定:有两边相等的三角形是等腰三角形.(定义)
(三线合一)
①边: 等腰三角形的两腰相等.
2、等腰三角形的判定:
②从角来判定: 有两个角相等的三角形是等腰三角形.(等角对等边)
回顾旧知
3、等边三角形的性质
①边:等边三角形的三边相等.
②角:等边三角形的三个角都相等, 并且每个角都等于60°.
③轴对称性:等边三角形每一条边上的高、中线和对角的平分线都三线合一.
等边三角形的判定?
一个三角形满足什么条件就是等边三角形
思考
探索新知
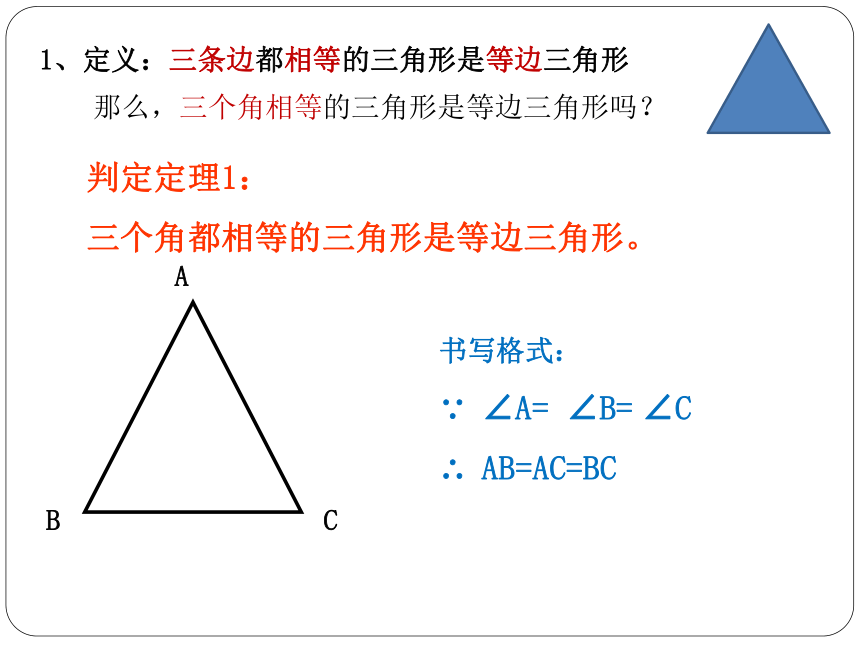
1、定义:三条边都相等的三角形是等边三角形
那么,三个角相等的三角形是等边三角形吗?
A
B
C
书写格式:
∵ ∠A= ∠B= ∠C
∴ AB=AC=BC
判定定理1:
三个角都相等的三角形是等边三角形。
一个等腰三角形满足什么条件就是等边三角形
思考
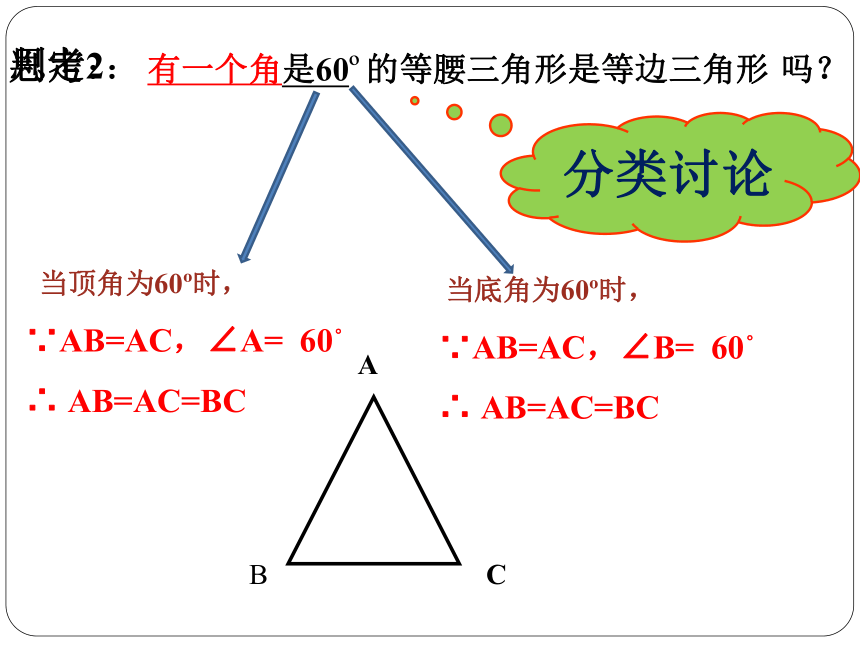
有一个角是60 的等腰三角形是等边三角形
A
B
C
∵AB=AC,∠A= 60。
∴ AB=AC=BC
∵AB=AC,∠B= 60。
∴ AB=AC=BC
当顶角为60 时,
思考:
分类讨论
当底角为60 时,
判定2:
吗?
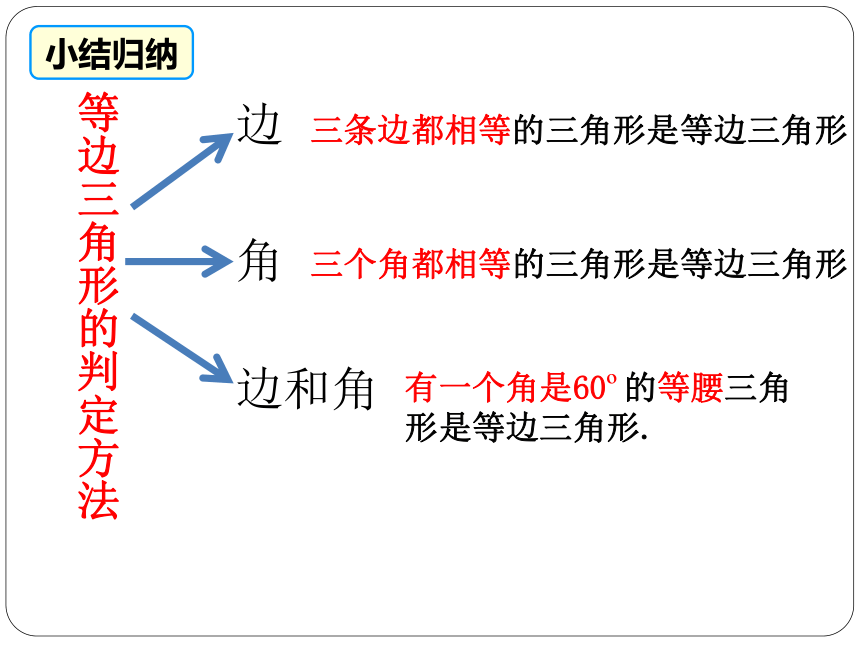
等边三角形的判定方法
边
角
边和角
三条边都相等的三角形是等边三角形
三个角都相等的三角形是等边三角形
有一个角是60 的等腰三角形是等边三角形.
小结归纳
例1.如图,△ABC是等边三角形,点E是AC上一点,∠1=∠2,BE=CD.请判断△ADE的形状,并说明理由.
解:△ADE是等边三角形.
理由如下:
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°
又∵∠1=∠2,BE=CD
∴△AEB≌△ADC(SAS)
∴AE=AD,
∠BAE=∠EAD=60°
∴△AED为等边三角形.
典例精析
用两个含有30 角的三角尺,你能拼成一个怎样的三角形?
300
300
能拼出一个等边三角形吗?说说你的理由.
做一做:
300
300
300
300
探索新知
能证明你的结论吗?
猜想: 在直角三角形中, 30 角所对的直角边等于斜边的一半.
由刚才的拼图你想到,在直角三角形中,30 角所对的直角边与斜边有怎样的大小关系?
猜一猜:
300
300
300
300
A
B
C
已知: 如图, 在Rt△ABC中,
∠ACB=90 ,∠A=30
求证: BC= AB.
求证: 在直角三角形中, 如果有一个锐角等于30°, 那么它所对的直角边等于斜边的一半.
300
A
B
C
D
分析:突破如何证明“线段的倍、分”问题
转 化
“线段相等”问题
延长BC至D, 使CD=BC, 连接AD
300
A
B
C
D
∵ ∠ACB=90 (已知)
∴∠ACD=90 (平角的定义)
在△ABC与△ADC中
∵BC=DC(作图)
∠ACB=∠ACD(已证)
AC=AC(公共边)
∴△ABC≌△ADC(SAS)
∴ AB=AD
∵∠ACB=90 , ∠A=30 (已知),
∴∠B=60° (直角三角形两锐角互余).
∴△ABD是等边三角形 (有一个角是60°的等腰三角形是等边三角形)
∴BC= BD= AB(等式性质).
证明: 延长BC至D,使CD=BC,连接AD
书写格式:
∵在Rt△ABC中, ∠A=30
∴BC= AB
(在直角三角形中, 30 角所对的直角边等于斜边的一半)
A
B
C
300
定理:在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半.
√
1)直角三角形中30 角所对的直角边等于另一
直角边的一半. 2)三角形中30 角所对的边等于最长边的一半。 3)直角三角形中最小的直角边是斜边的一半。 4)直角三角形的斜边是30 角所对直角边的2倍.
判 断
A
C
B
D
150
150
已知:如图,△ABC中,AB=AC,
∠B= 15 , CD是腰AB上的高
证明: ∵∠B=∠ACB=15 (已知),
∴∠DAC=∠B+∠ACB= 15 + 15 = 30 (三角形的一个外角,等于和不相邻的两内角的和).
例2. 求证: 如果等腰三角形的底角为15 , 那么腰上的高是腰长的一半.
求证: CD= AC
∴CD= AC (在直角三角形中, 如果有一个锐角等于30°, 那么它所对的直角边等于斜边的一半).
典例精析
小结:等腰三角形中见15°则有30°,从而得到线段关系。
典例精析
小结:直角三角形中出现斜边上的高时,观察锐角之间关系。
例3. 如图,在△ABC中,∠BAC=90 ,
AD是高,∠B=30 ,
求证:DC= BC.
证明:∵∠BAC=90°,∠B=30°,∴AC= BC
∵∠BAC=90°,∠B=30°,∴∠C=60°
∵AD是高,∴∠ADC=90°.∴∠DAC=30°
∴DC= AC,即DC= AC = × BC= BC
C
B
A
拓展:
如图, ∠C=90 ,∠BAC=30 ,设BC=x,则AB=?AC=
x
小结:30°的直角三角形三条边长比值是固定的,只需已知一条边长即可求剩下两条边长。
命题:
在直角三角形中, 如果一条直角边等于斜边的一半, 那么它所对的锐角等于30 . 是真命题吗
如果是, 请你证明它.
A
B
C
已知: 如图, 在△ABC中, ∠ACB=90°, BC=
求证: ∠A=30°.
逆向思维
探索新知
A
B
C
D
证明: 如图, 延长BC至D, 使CD=BC, 连接AD.
已知: 如图, 在△ABC中, ∠ACB=90°, BC= AB.
求证: ∠A=30°.
在△ABC和△ADC中,
∵BC=CD, ∠ACB=∠ACD= 90°, AC=AC
∴ △ABC≌△ADC(SAS) ,
∴ AB=AD
又∵BC= AB ,BC= BD
∴AB=BD
∴AB=BD=AD
∴△ABD是等边三角形.
∴∠B=60°
∴∠A=30°
1、等边三角形的判定方法:
(1)等边三角形的定义:三边相等的三角形是等边三角形
(2)定理: 三个角都相等的三角形是等边三角形.
(3)定理: 有一个角是60°的等腰三角形是等边三角形.
2、含有30 角的直角三角形的性质:
(1)定理: 在直角三角形中, 如果有一个锐角等于30°, 那么它所对的直角边等于斜边的一半.
(2)逆定理: 在直角三角形中, 如果一条直角边等于斜边的一半, 那么它所对的锐角等于30°.
课堂小结
谢谢!再见!
1.1 等腰三角形
北师大版 数学八年级下册 第一章 三角形的证明
1.理解等边三角形的判别条件及其证明;并能利用定理解决一些简单的问题.
2.理解含有30 角的直角三角形性质及其证明,并能有意识渗透逆向思维的思想。
学习目标
②角: 等腰三角形的两个底角相等.
(等边对等角)
③轴对称性: 等腰三角形顶角的平分线、底边
上的中线、底边上的高线互相重合 .
1、等腰三角形的性质:
①从边来判定:有两边相等的三角形是等腰三角形.(定义)
(三线合一)
①边: 等腰三角形的两腰相等.
2、等腰三角形的判定:
②从角来判定: 有两个角相等的三角形是等腰三角形.(等角对等边)
回顾旧知
3、等边三角形的性质
①边:等边三角形的三边相等.
②角:等边三角形的三个角都相等, 并且每个角都等于60°.
③轴对称性:等边三角形每一条边上的高、中线和对角的平分线都三线合一.
等边三角形的判定?
一个三角形满足什么条件就是等边三角形
思考
探索新知
1、定义:三条边都相等的三角形是等边三角形
那么,三个角相等的三角形是等边三角形吗?
A
B
C
书写格式:
∵ ∠A= ∠B= ∠C
∴ AB=AC=BC
判定定理1:
三个角都相等的三角形是等边三角形。
一个等腰三角形满足什么条件就是等边三角形
思考
有一个角是60 的等腰三角形是等边三角形
A
B
C
∵AB=AC,∠A= 60。
∴ AB=AC=BC
∵AB=AC,∠B= 60。
∴ AB=AC=BC
当顶角为60 时,
思考:
分类讨论
当底角为60 时,
判定2:
吗?
等边三角形的判定方法
边
角
边和角
三条边都相等的三角形是等边三角形
三个角都相等的三角形是等边三角形
有一个角是60 的等腰三角形是等边三角形.
小结归纳
例1.如图,△ABC是等边三角形,点E是AC上一点,∠1=∠2,BE=CD.请判断△ADE的形状,并说明理由.
解:△ADE是等边三角形.
理由如下:
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°
又∵∠1=∠2,BE=CD
∴△AEB≌△ADC(SAS)
∴AE=AD,
∠BAE=∠EAD=60°
∴△AED为等边三角形.
典例精析
用两个含有30 角的三角尺,你能拼成一个怎样的三角形?
300
300
能拼出一个等边三角形吗?说说你的理由.
做一做:
300
300
300
300
探索新知
能证明你的结论吗?
猜想: 在直角三角形中, 30 角所对的直角边等于斜边的一半.
由刚才的拼图你想到,在直角三角形中,30 角所对的直角边与斜边有怎样的大小关系?
猜一猜:
300
300
300
300
A
B
C
已知: 如图, 在Rt△ABC中,
∠ACB=90 ,∠A=30
求证: BC= AB.
求证: 在直角三角形中, 如果有一个锐角等于30°, 那么它所对的直角边等于斜边的一半.
300
A
B
C
D
分析:突破如何证明“线段的倍、分”问题
转 化
“线段相等”问题
延长BC至D, 使CD=BC, 连接AD
300
A
B
C
D
∵ ∠ACB=90 (已知)
∴∠ACD=90 (平角的定义)
在△ABC与△ADC中
∵BC=DC(作图)
∠ACB=∠ACD(已证)
AC=AC(公共边)
∴△ABC≌△ADC(SAS)
∴ AB=AD
∵∠ACB=90 , ∠A=30 (已知),
∴∠B=60° (直角三角形两锐角互余).
∴△ABD是等边三角形 (有一个角是60°的等腰三角形是等边三角形)
∴BC= BD= AB(等式性质).
证明: 延长BC至D,使CD=BC,连接AD
书写格式:
∵在Rt△ABC中, ∠A=30
∴BC= AB
(在直角三角形中, 30 角所对的直角边等于斜边的一半)
A
B
C
300
定理:在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半.
√
1)直角三角形中30 角所对的直角边等于另一
直角边的一半. 2)三角形中30 角所对的边等于最长边的一半。 3)直角三角形中最小的直角边是斜边的一半。 4)直角三角形的斜边是30 角所对直角边的2倍.
判 断
A
C
B
D
150
150
已知:如图,△ABC中,AB=AC,
∠B= 15 , CD是腰AB上的高
证明: ∵∠B=∠ACB=15 (已知),
∴∠DAC=∠B+∠ACB= 15 + 15 = 30 (三角形的一个外角,等于和不相邻的两内角的和).
例2. 求证: 如果等腰三角形的底角为15 , 那么腰上的高是腰长的一半.
求证: CD= AC
∴CD= AC (在直角三角形中, 如果有一个锐角等于30°, 那么它所对的直角边等于斜边的一半).
典例精析
小结:等腰三角形中见15°则有30°,从而得到线段关系。
典例精析
小结:直角三角形中出现斜边上的高时,观察锐角之间关系。
例3. 如图,在△ABC中,∠BAC=90 ,
AD是高,∠B=30 ,
求证:DC= BC.
证明:∵∠BAC=90°,∠B=30°,∴AC= BC
∵∠BAC=90°,∠B=30°,∴∠C=60°
∵AD是高,∴∠ADC=90°.∴∠DAC=30°
∴DC= AC,即DC= AC = × BC= BC
C
B
A
拓展:
如图, ∠C=90 ,∠BAC=30 ,设BC=x,则AB=?AC=
x
小结:30°的直角三角形三条边长比值是固定的,只需已知一条边长即可求剩下两条边长。
命题:
在直角三角形中, 如果一条直角边等于斜边的一半, 那么它所对的锐角等于30 . 是真命题吗
如果是, 请你证明它.
A
B
C
已知: 如图, 在△ABC中, ∠ACB=90°, BC=
求证: ∠A=30°.
逆向思维
探索新知
A
B
C
D
证明: 如图, 延长BC至D, 使CD=BC, 连接AD.
已知: 如图, 在△ABC中, ∠ACB=90°, BC= AB.
求证: ∠A=30°.
在△ABC和△ADC中,
∵BC=CD, ∠ACB=∠ACD= 90°, AC=AC
∴ △ABC≌△ADC(SAS) ,
∴ AB=AD
又∵BC= AB ,BC= BD
∴AB=BD
∴AB=BD=AD
∴△ABD是等边三角形.
∴∠B=60°
∴∠A=30°
1、等边三角形的判定方法:
(1)等边三角形的定义:三边相等的三角形是等边三角形
(2)定理: 三个角都相等的三角形是等边三角形.
(3)定理: 有一个角是60°的等腰三角形是等边三角形.
2、含有30 角的直角三角形的性质:
(1)定理: 在直角三角形中, 如果有一个锐角等于30°, 那么它所对的直角边等于斜边的一半.
(2)逆定理: 在直角三角形中, 如果一条直角边等于斜边的一半, 那么它所对的锐角等于30°.
课堂小结
谢谢!再见!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
