2022届艺考生高考数学中点弦问题 教案 (含答案解析)
文档属性
| 名称 | 2022届艺考生高考数学中点弦问题 教案 (含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 594.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 16:18:58 | ||
图片预览




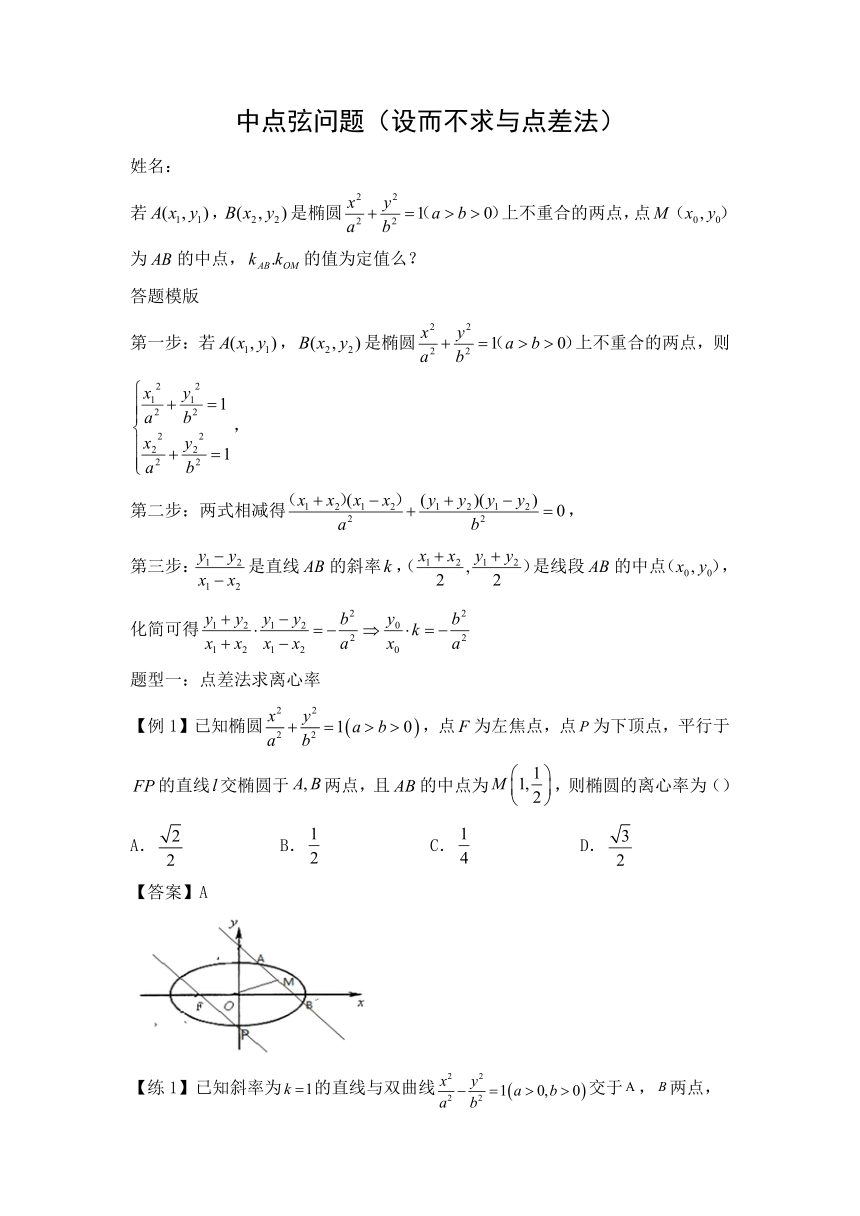
文档简介
2022届艺考生高考数学中点弦问题教案
中点弦问题(设而不求与点差法)
姓名:
若,是椭圆上不重合的两点,点为的中点,的值为定值么?
答题模版
第一步:若,是椭圆上不重合的两点,则,
第二步:两式相减得,
第三步:是直线的斜率,是线段的中点,化简可得
题型一:点差法求离心率
【例1】已知椭圆,点为左焦点,点为下顶点,平行于的直线交椭圆于两点,且的中点为,则椭圆的离心率为()
A. B. C. D.
【练1】已知斜率为的直线与双曲线交于,两点,若,的中点为,则双曲线的离心率为
【练2】已知椭圆:的左焦点为,过作一条倾斜角为的直线与椭圆交于,两点,若为线段的中点,则椭圆的离心率是_________.
【提升】在平面直角坐标系中,已知椭圆的离心率为,为椭圆的一条弦(不经过原点),直线经过弦的中点,与椭圆交于、两点,设直线的斜率为.
(1)若点的坐标为,求椭圆的方程;
(2)求证:为定值;
题型二:求中点弦直线斜率
【例2】已知椭圆C:的离心率为,直线l与椭圆C交于两点,且线段的中点为,则直线l的斜率为( )
A. B. C. D.1
【练1】双曲线与直线交于两点, 且线段中点为,为坐标原点,则直线的斜率是______.
【练2】设椭圆过点,离心率为
(1)求C的方程;
(2)求过点且以M点为中点的弦的方程.
【提升】已知椭圆的一个顶点为,离心率,直线交椭圆于两点,如果的重心恰好为椭圆的右焦点,直线方程为________.
题型三:求曲线的标准方程
【例3】若双曲线的中心为原点,是双曲线的焦点,过F直线l与双曲线交于M,N两点,且MN的中点为,则双曲线的方程为
A. B. C. D.
【练1】已知椭圆的左、右焦点分别为,过左焦点作斜率为-2的直线与椭圆交于A,B两点,P是AB的中点,O为坐标原点,若直线OP的斜率为,则a的值是______.
【练2】已知椭圆的离心率为,点是椭圆上的两个点,点是线段的中点.求椭圆的标准方程;
【提升】已知椭圆中心在原点,且一个焦点为,直线与其相交于、两点,中点的横坐标为,则此椭圆的方程是( )
A. B. C. D.
当堂检测
1.已知椭圆,的一条弦所在的直线方程是,弦的中点坐标是,则椭圆的离心率是( )
A. B. C. D.
2.如果椭圆的弦被点平分,则这条弦所在的直线方程是( )
A. B. C. D.
3.若双曲线的中心为原点,是双曲线的焦点,过的直线与双曲线相交于,两点,且的中点为则双曲线的方程为( )
A. B. C. D.
4.椭圆mx2+ny2=1与直线y=1-x交于M,N两点,过原点与线段MN中点所在直线的斜率为,则 的值是( )
A. B. C. D.
5.已知椭圆的长轴长为,且短轴长是长轴长的一半.
(1)求椭圆的方程;
(2)经过点作直线,交椭圆于、两点.如果恰好是线段的中点,求直线的方程.
【提升练习】
1.直线交椭圆于两点,若线段中点的横坐标为1,则( )
A.-2 B.-1 C.1 D.2
2.已知斜率为的直线与椭圆交于,两点.线段的中点为.证明:;
中点弦问题(设而不求与点差法)
姓名:
若,是椭圆上不重合的两点,点为的中点,的值为定值么?
答题模版
第一步:若,是椭圆上不重合的两点,则,
第二步:两式相减得,
第三步:是直线的斜率,是线段的中点,化简可得
题型一:点差法求离心率
【例1】已知椭圆,点为左焦点,点为下顶点,平行于的直线交椭圆于两点,且的中点为,则椭圆的离心率为()
A. B. C. D.
【答案】A
【练1】已知斜率为的直线与双曲线交于,两点,若,的中点为,则双曲线的离心率为
【答案】
【练2】已知椭圆:的左焦点为,过作一条倾斜角为的直线与椭圆交于,两点,若为线段的中点,则椭圆的离心率是_________.
【答案】
【提升】在平面直角坐标系中,已知椭圆的离心率为,为椭圆的一条弦(不经过原点),直线经过弦的中点,与椭圆交于、两点,设直线的斜率为.
(1)若点的坐标为,求椭圆的方程;
(2)求证:为定值;
【答案】(1);(2)证明见解析;
【详解】
由已知条件得,解得,因此,椭圆的方程为;
(2)设点、,则线段的中点坐标为,
,.
由题意可得,,,
由于点、都在椭圆上,则,
两式作差得,(定值);
题型二:求中点弦直线斜率
【例2】已知椭圆C:的离心率为,直线l与椭圆C交于两点,且线段的中点为,则直线l的斜率为( )
A. B. C. D.1
【答案】C
【练1】双曲线与直线交于两点, 且线段中点为,为坐标原点,则直线的斜率是______.
【答案】
【练2】设椭圆过点,离心率为
(1)求C的方程;
(2)求过点且以M点为中点的弦的方程.
【答案】(1);(2).
【详解】
(1)将代入C的方程得,
∴=4,又 得,
即,∴,∴C的方程为.
(2)设直线与C的交点为A,B,代入椭圆方程得
,作差化简可得,即,又,
则,
以M点为中点的弦的方程: ,即:.
【提升】已知椭圆的一个顶点为,离心率,直线交椭圆于两点,如果的重心恰好为椭圆的右焦点,直线方程为________.
【答案】
题型三:求曲线的标准方程
【例3】若双曲线的中心为原点,是双曲线的焦点,过F直线l与双曲线交于M,N两点,且MN的中点为,则双曲线的方程为
A. B. C. D.
【答案】D
【练1】已知椭圆的左、右焦点分别为,过左焦点作斜率为-2的直线与椭圆交于A,B两点,P是AB的中点,O为坐标原点,若直线OP的斜率为,则a的值是______.
【答案】2
【练2】已知椭圆的离心率为,点是椭圆上的两个点,点是线段的中点.求椭圆的标准方程;
【答案】
【详解】
由条件知,,,
所以,解得,
所以椭圆的标准方程为;
【提升】已知椭圆中心在原点,且一个焦点为,直线与其相交于、两点,中点的横坐标为,则此椭圆的方程是( )
A. B. C. D.
【答案】C
当堂检测
1.已知椭圆,的一条弦所在的直线方程是,弦的中点坐标是,则椭圆的离心率是( )
A. B. C. D.
【答案】C
2.如果椭圆的弦被点平分,则这条弦所在的直线方程是( )
A. B. C. D.
【答案】D
3.若双曲线的中心为原点,是双曲线的焦点,过的直线与双曲线相交于,两点,且的中点为则双曲线的方程为( )
A. B. C. D.
【答案】B
4.椭圆mx2+ny2=1与直线y=1-x交于M,N两点,过原点与线段MN中点所在直线的斜率为,则 的值是( )
A. B. C. D.
【答案】A
5.已知椭圆的长轴长为,且短轴长是长轴长的一半.
(1)求椭圆的方程;
(2)经过点作直线,交椭圆于、两点.如果恰好是线段的中点,求直线的方程.
【答案】(1);(2).
【详解】
(1)根据题意,椭圆的长轴长为,且短轴长是长轴长的一半.
即,则,,则,因此,椭圆的方程为;
(2)由(1)得椭圆的方程为,设点、,
由于点为线段的中点,则,得.
由于点、在椭圆上,则,两个等式相减得,
即,即,
所以,直线的斜率为.
因此,直线的方程为,即.
【提升练习】
1.直线交椭圆于两点,若线段中点的横坐标为1,则( )
A.-2 B.-1 C.1 D.2
【答案】A
2.已知斜率为的直线与椭圆交于,两点.线段的中点为.证明:;
详解:设,,则,.
两式相减,并由得.
由题设知,,于是.
由题设得,故.
中点弦问题(设而不求与点差法)
姓名:
若,是椭圆上不重合的两点,点为的中点,的值为定值么?
答题模版
第一步:若,是椭圆上不重合的两点,则,
第二步:两式相减得,
第三步:是直线的斜率,是线段的中点,化简可得
题型一:点差法求离心率
【例1】已知椭圆,点为左焦点,点为下顶点,平行于的直线交椭圆于两点,且的中点为,则椭圆的离心率为()
A. B. C. D.
【练1】已知斜率为的直线与双曲线交于,两点,若,的中点为,则双曲线的离心率为
【练2】已知椭圆:的左焦点为,过作一条倾斜角为的直线与椭圆交于,两点,若为线段的中点,则椭圆的离心率是_________.
【提升】在平面直角坐标系中,已知椭圆的离心率为,为椭圆的一条弦(不经过原点),直线经过弦的中点,与椭圆交于、两点,设直线的斜率为.
(1)若点的坐标为,求椭圆的方程;
(2)求证:为定值;
题型二:求中点弦直线斜率
【例2】已知椭圆C:的离心率为,直线l与椭圆C交于两点,且线段的中点为,则直线l的斜率为( )
A. B. C. D.1
【练1】双曲线与直线交于两点, 且线段中点为,为坐标原点,则直线的斜率是______.
【练2】设椭圆过点,离心率为
(1)求C的方程;
(2)求过点且以M点为中点的弦的方程.
【提升】已知椭圆的一个顶点为,离心率,直线交椭圆于两点,如果的重心恰好为椭圆的右焦点,直线方程为________.
题型三:求曲线的标准方程
【例3】若双曲线的中心为原点,是双曲线的焦点,过F直线l与双曲线交于M,N两点,且MN的中点为,则双曲线的方程为
A. B. C. D.
【练1】已知椭圆的左、右焦点分别为,过左焦点作斜率为-2的直线与椭圆交于A,B两点,P是AB的中点,O为坐标原点,若直线OP的斜率为,则a的值是______.
【练2】已知椭圆的离心率为,点是椭圆上的两个点,点是线段的中点.求椭圆的标准方程;
【提升】已知椭圆中心在原点,且一个焦点为,直线与其相交于、两点,中点的横坐标为,则此椭圆的方程是( )
A. B. C. D.
当堂检测
1.已知椭圆,的一条弦所在的直线方程是,弦的中点坐标是,则椭圆的离心率是( )
A. B. C. D.
2.如果椭圆的弦被点平分,则这条弦所在的直线方程是( )
A. B. C. D.
3.若双曲线的中心为原点,是双曲线的焦点,过的直线与双曲线相交于,两点,且的中点为则双曲线的方程为( )
A. B. C. D.
4.椭圆mx2+ny2=1与直线y=1-x交于M,N两点,过原点与线段MN中点所在直线的斜率为,则 的值是( )
A. B. C. D.
5.已知椭圆的长轴长为,且短轴长是长轴长的一半.
(1)求椭圆的方程;
(2)经过点作直线,交椭圆于、两点.如果恰好是线段的中点,求直线的方程.
【提升练习】
1.直线交椭圆于两点,若线段中点的横坐标为1,则( )
A.-2 B.-1 C.1 D.2
2.已知斜率为的直线与椭圆交于,两点.线段的中点为.证明:;
中点弦问题(设而不求与点差法)
姓名:
若,是椭圆上不重合的两点,点为的中点,的值为定值么?
答题模版
第一步:若,是椭圆上不重合的两点,则,
第二步:两式相减得,
第三步:是直线的斜率,是线段的中点,化简可得
题型一:点差法求离心率
【例1】已知椭圆,点为左焦点,点为下顶点,平行于的直线交椭圆于两点,且的中点为,则椭圆的离心率为()
A. B. C. D.
【答案】A
【练1】已知斜率为的直线与双曲线交于,两点,若,的中点为,则双曲线的离心率为
【答案】
【练2】已知椭圆:的左焦点为,过作一条倾斜角为的直线与椭圆交于,两点,若为线段的中点,则椭圆的离心率是_________.
【答案】
【提升】在平面直角坐标系中,已知椭圆的离心率为,为椭圆的一条弦(不经过原点),直线经过弦的中点,与椭圆交于、两点,设直线的斜率为.
(1)若点的坐标为,求椭圆的方程;
(2)求证:为定值;
【答案】(1);(2)证明见解析;
【详解】
由已知条件得,解得,因此,椭圆的方程为;
(2)设点、,则线段的中点坐标为,
,.
由题意可得,,,
由于点、都在椭圆上,则,
两式作差得,(定值);
题型二:求中点弦直线斜率
【例2】已知椭圆C:的离心率为,直线l与椭圆C交于两点,且线段的中点为,则直线l的斜率为( )
A. B. C. D.1
【答案】C
【练1】双曲线与直线交于两点, 且线段中点为,为坐标原点,则直线的斜率是______.
【答案】
【练2】设椭圆过点,离心率为
(1)求C的方程;
(2)求过点且以M点为中点的弦的方程.
【答案】(1);(2).
【详解】
(1)将代入C的方程得,
∴=4,又 得,
即,∴,∴C的方程为.
(2)设直线与C的交点为A,B,代入椭圆方程得
,作差化简可得,即,又,
则,
以M点为中点的弦的方程: ,即:.
【提升】已知椭圆的一个顶点为,离心率,直线交椭圆于两点,如果的重心恰好为椭圆的右焦点,直线方程为________.
【答案】
题型三:求曲线的标准方程
【例3】若双曲线的中心为原点,是双曲线的焦点,过F直线l与双曲线交于M,N两点,且MN的中点为,则双曲线的方程为
A. B. C. D.
【答案】D
【练1】已知椭圆的左、右焦点分别为,过左焦点作斜率为-2的直线与椭圆交于A,B两点,P是AB的中点,O为坐标原点,若直线OP的斜率为,则a的值是______.
【答案】2
【练2】已知椭圆的离心率为,点是椭圆上的两个点,点是线段的中点.求椭圆的标准方程;
【答案】
【详解】
由条件知,,,
所以,解得,
所以椭圆的标准方程为;
【提升】已知椭圆中心在原点,且一个焦点为,直线与其相交于、两点,中点的横坐标为,则此椭圆的方程是( )
A. B. C. D.
【答案】C
当堂检测
1.已知椭圆,的一条弦所在的直线方程是,弦的中点坐标是,则椭圆的离心率是( )
A. B. C. D.
【答案】C
2.如果椭圆的弦被点平分,则这条弦所在的直线方程是( )
A. B. C. D.
【答案】D
3.若双曲线的中心为原点,是双曲线的焦点,过的直线与双曲线相交于,两点,且的中点为则双曲线的方程为( )
A. B. C. D.
【答案】B
4.椭圆mx2+ny2=1与直线y=1-x交于M,N两点,过原点与线段MN中点所在直线的斜率为,则 的值是( )
A. B. C. D.
【答案】A
5.已知椭圆的长轴长为,且短轴长是长轴长的一半.
(1)求椭圆的方程;
(2)经过点作直线,交椭圆于、两点.如果恰好是线段的中点,求直线的方程.
【答案】(1);(2).
【详解】
(1)根据题意,椭圆的长轴长为,且短轴长是长轴长的一半.
即,则,,则,因此,椭圆的方程为;
(2)由(1)得椭圆的方程为,设点、,
由于点为线段的中点,则,得.
由于点、在椭圆上,则,两个等式相减得,
即,即,
所以,直线的斜率为.
因此,直线的方程为,即.
【提升练习】
1.直线交椭圆于两点,若线段中点的横坐标为1,则( )
A.-2 B.-1 C.1 D.2
【答案】A
2.已知斜率为的直线与椭圆交于,两点.线段的中点为.证明:;
详解:设,,则,.
两式相减,并由得.
由题设知,,于是.
由题设得,故.
同课章节目录
