2021-2022学年苏科版数学九年级上册1.4用一元二次方程解决问题同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版数学九年级上册1.4用一元二次方程解决问题同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 132.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 08:44:40 | ||
图片预览


文档简介
1.4用一元二次方程解决问题
一、单选题
1.为防治雾霾,保护环境,某市掀起“爱绿护绿”热潮,经过两年时间,绿地面积增加了21%,这两年绿地面积的平均增长率是( )
A.12% B.30% C.10% D.22%
2.某市2020年投入了教育专项经费7200万元,用于发展本市的教育,预计到2022年将投入教育专项经费9800万元,若每年增长率都为x,下列方程正确的是( )
A.7200(1+x)=9800
B.7200(1+x)2=9800
C.7200(1+x)+7200(1+x)2=9800
D.7200x2=9800
3.书法兴趣小组在中秋节这一天人人相互送一个月饼,共送出72个月饼,书法兴趣小组人数个数是( )
A.7 B.8 C.9 D.6
4.2021年是中国共产党成立100周年,某中学发起了“热爱祖国,感恩共产党”说句心里话征集活动.学校学生会主席要求征集活动在微信朋友圈里进行传递,规则为:将征集活动发在自己的朋友图,再邀请n个好友转发征集活动,每个好友转发朋友圈,又邀请n个互不相同的好友转发征集活动,以此类推,已知经过两轮传递后,共有931人参与了传递活动,则方程列为( )
A.(1+n)2=931 B.n(n﹣1)=931 C.1+n+n2=931 D.n+n2=931
5.某公司今年4月的营业额为2500万元,按计划第二季度的总营业额要达到9100万元,设该公司5、6两月的营业额的月平均增长率为x.根据题意列方程,则下列方程正确的是( )
A.
B.
C.
D.
6.如图,在长为54米、宽为38米的矩形草地上修同样宽的路,余下部分种植草坪.要使草坪的面积为1800平方米,设道路的宽为x米,则可列方程为( )
A. B.
C. D.
7.一个两位数的两个数字的和为9,把这个两位数的个位数字与十位数字互换得到一个新的两位数,它与原两位数的积为1458,设原两位数的个位数字为x,则可列方程( )
A. B.
C. D.
8.如图,这是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…,第行有个点…,前行的点数和不能是以下哪个结果 ( )
A.741 B.600 C.465 D.300
9.如图,在中,,,.动点,分别从点,同时开始移动,点的速度为秒,点的速度为秒,点移动到点后停止,点也随之停止运动.下列时间瞬间中,能使的面积为的是( )
A.2秒钟 B.3秒钟 C.4秒钟 D.5秒钟
10.某品牌钢笔进价8元,按10元1支出售时每天能卖出20支,市场调查发现如果每支每涨价1元,每天就少卖出2支,为了每天获得最大利润,其售价应定为( )
A.11元 B.12元 C.13元 D.14元
二、填空题
11.某装饰材料原来准备以每平方米元的销售.为了加快资金周转,商场经过两次下调后,决定以每平方米元销售.设平均每次下调的百分率,则可列方程为________.
12.如图,某校要在长为,宽为的长方形操场上修筑宽度相同的道路(图中阴影部分),在余下的空白部分种上草坪,要使草坪的面积为,设道路宽为米,可列出方程_____________________.
13.某校九(6)班学生毕业时,每个同学都要给其他同学写一份毕业留言作为纪念,全班学生共写了930份留言,如果全班有x名学生,根据题意,列出方程为_________.
14.一个两位数,它的十位数字比个位数字大,个位数字与十位数字的平方和比这个两位数小,则这个两位数是________.
15.某医院内科病房有护士人,每2人一班,轮流值班,每8小时换班一次,某两人同值一班后,到下次两人同班,最长需要的天数是70天,则______.
三、解答题
16.张师傅今年初开了一家药店,二月份开始盈利,二月份的盈利是6000元,四月份的盈利达到8640元,且从今年二月到四月,每月盈利的平均增长率都相同.
(1)求每月盈利的平均增长率;
(2)按照这个平均增长率,预计今年五月份的盈利能达到多少元?
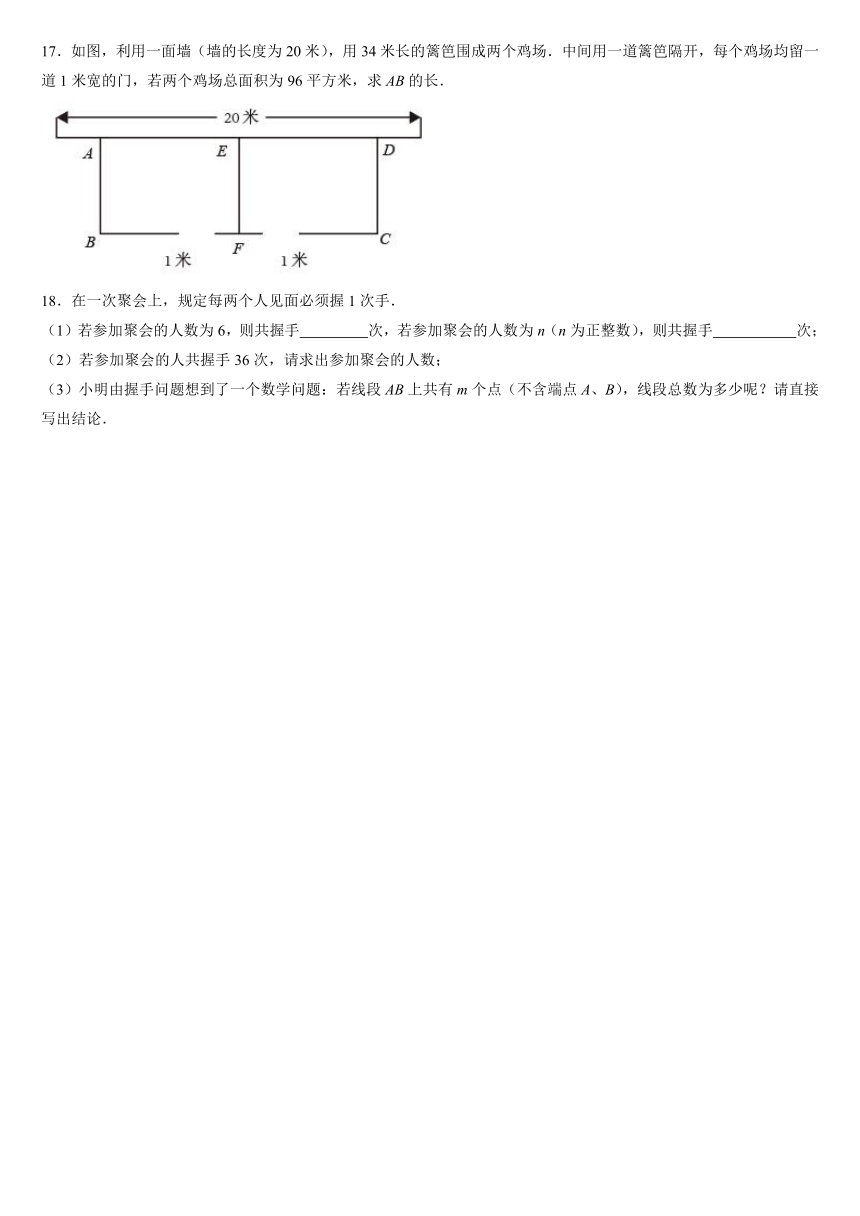
17.如图,利用一面墙(墙的长度为20米),用34米长的篱笆围成两个鸡场.中间用一道篱笆隔开,每个鸡场均留一道1米宽的门,若两个鸡场总面积为96平方米,求AB的长.
18.在一次聚会上,规定每两个人见面必须握1次手.
(1)若参加聚会的人数为6,则共握手 次,若参加聚会的人数为n(n为正整数),则共握手 次;
(2)若参加聚会的人共握手36次,请求出参加聚会的人数;
(3)小明由握手问题想到了一个数学问题:若线段AB上共有m个点(不含端点A、B),线段总数为多少呢?请直接写出结论.
参考答案
1.C
2.解:依题意得:7200(1+x)2=9800.
故选:B.
3.解:设书法兴趣小组共有x人,则每人需送出(x﹣1)个月饼,
依题意得:x(x﹣1)=72,
整理得:x2﹣x﹣72=0,
解得:x1=9,x2=﹣8(不合题意,舍去).
故选:C.
4.解:由题意,得
n2+n+1=931,
故选:C.
5.D
6.A
解:设道路的宽为x米,
根据题意得(54-x)(38-x)=1800.
故选A.
7.C
解:由题意得:原两位数的十位数字为9-x,则有,
;
故选C.
8.B
解:通过观察图形可知:
第一行有1个点,第二行有2个点…第n行有n个点,
则前5行共有(1+2+3+4+5)个点,
前10行共有(1+2+3+4+5+6+7+8+9+10)个点,
前n行共有1+2+3+4+5+…+n=n(n+1)个点,
其中n为正整数,
∴当n(n+1)=741时,解得:(舍),,
当n(n+1)=600时,解得: (舍),
当n(n+1)=465时,解得:(舍),,
当n(n+1)=300时,解得:(舍),,
故选:B.
9.B
10.D
11.
12.
13.
14.
15.21
16.(1)每月盈利的平均增长率为20%;(2)按照这个平均增长率,预计今年五月份这家商店的盈利将达到10368元.
17.AB的长为8米.
18.(1)15,;(2)参加聚会的人数为9人;(3)线段数为
一、单选题
1.为防治雾霾,保护环境,某市掀起“爱绿护绿”热潮,经过两年时间,绿地面积增加了21%,这两年绿地面积的平均增长率是( )
A.12% B.30% C.10% D.22%
2.某市2020年投入了教育专项经费7200万元,用于发展本市的教育,预计到2022年将投入教育专项经费9800万元,若每年增长率都为x,下列方程正确的是( )
A.7200(1+x)=9800
B.7200(1+x)2=9800
C.7200(1+x)+7200(1+x)2=9800
D.7200x2=9800
3.书法兴趣小组在中秋节这一天人人相互送一个月饼,共送出72个月饼,书法兴趣小组人数个数是( )
A.7 B.8 C.9 D.6
4.2021年是中国共产党成立100周年,某中学发起了“热爱祖国,感恩共产党”说句心里话征集活动.学校学生会主席要求征集活动在微信朋友圈里进行传递,规则为:将征集活动发在自己的朋友图,再邀请n个好友转发征集活动,每个好友转发朋友圈,又邀请n个互不相同的好友转发征集活动,以此类推,已知经过两轮传递后,共有931人参与了传递活动,则方程列为( )
A.(1+n)2=931 B.n(n﹣1)=931 C.1+n+n2=931 D.n+n2=931
5.某公司今年4月的营业额为2500万元,按计划第二季度的总营业额要达到9100万元,设该公司5、6两月的营业额的月平均增长率为x.根据题意列方程,则下列方程正确的是( )
A.
B.
C.
D.
6.如图,在长为54米、宽为38米的矩形草地上修同样宽的路,余下部分种植草坪.要使草坪的面积为1800平方米,设道路的宽为x米,则可列方程为( )
A. B.
C. D.
7.一个两位数的两个数字的和为9,把这个两位数的个位数字与十位数字互换得到一个新的两位数,它与原两位数的积为1458,设原两位数的个位数字为x,则可列方程( )
A. B.
C. D.
8.如图,这是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…,第行有个点…,前行的点数和不能是以下哪个结果 ( )
A.741 B.600 C.465 D.300
9.如图,在中,,,.动点,分别从点,同时开始移动,点的速度为秒,点的速度为秒,点移动到点后停止,点也随之停止运动.下列时间瞬间中,能使的面积为的是( )
A.2秒钟 B.3秒钟 C.4秒钟 D.5秒钟
10.某品牌钢笔进价8元,按10元1支出售时每天能卖出20支,市场调查发现如果每支每涨价1元,每天就少卖出2支,为了每天获得最大利润,其售价应定为( )
A.11元 B.12元 C.13元 D.14元
二、填空题
11.某装饰材料原来准备以每平方米元的销售.为了加快资金周转,商场经过两次下调后,决定以每平方米元销售.设平均每次下调的百分率,则可列方程为________.
12.如图,某校要在长为,宽为的长方形操场上修筑宽度相同的道路(图中阴影部分),在余下的空白部分种上草坪,要使草坪的面积为,设道路宽为米,可列出方程_____________________.
13.某校九(6)班学生毕业时,每个同学都要给其他同学写一份毕业留言作为纪念,全班学生共写了930份留言,如果全班有x名学生,根据题意,列出方程为_________.
14.一个两位数,它的十位数字比个位数字大,个位数字与十位数字的平方和比这个两位数小,则这个两位数是________.
15.某医院内科病房有护士人,每2人一班,轮流值班,每8小时换班一次,某两人同值一班后,到下次两人同班,最长需要的天数是70天,则______.
三、解答题
16.张师傅今年初开了一家药店,二月份开始盈利,二月份的盈利是6000元,四月份的盈利达到8640元,且从今年二月到四月,每月盈利的平均增长率都相同.
(1)求每月盈利的平均增长率;
(2)按照这个平均增长率,预计今年五月份的盈利能达到多少元?
17.如图,利用一面墙(墙的长度为20米),用34米长的篱笆围成两个鸡场.中间用一道篱笆隔开,每个鸡场均留一道1米宽的门,若两个鸡场总面积为96平方米,求AB的长.
18.在一次聚会上,规定每两个人见面必须握1次手.
(1)若参加聚会的人数为6,则共握手 次,若参加聚会的人数为n(n为正整数),则共握手 次;
(2)若参加聚会的人共握手36次,请求出参加聚会的人数;
(3)小明由握手问题想到了一个数学问题:若线段AB上共有m个点(不含端点A、B),线段总数为多少呢?请直接写出结论.
参考答案
1.C
2.解:依题意得:7200(1+x)2=9800.
故选:B.
3.解:设书法兴趣小组共有x人,则每人需送出(x﹣1)个月饼,
依题意得:x(x﹣1)=72,
整理得:x2﹣x﹣72=0,
解得:x1=9,x2=﹣8(不合题意,舍去).
故选:C.
4.解:由题意,得
n2+n+1=931,
故选:C.
5.D
6.A
解:设道路的宽为x米,
根据题意得(54-x)(38-x)=1800.
故选A.
7.C
解:由题意得:原两位数的十位数字为9-x,则有,
;
故选C.
8.B
解:通过观察图形可知:
第一行有1个点,第二行有2个点…第n行有n个点,
则前5行共有(1+2+3+4+5)个点,
前10行共有(1+2+3+4+5+6+7+8+9+10)个点,
前n行共有1+2+3+4+5+…+n=n(n+1)个点,
其中n为正整数,
∴当n(n+1)=741时,解得:(舍),,
当n(n+1)=600时,解得: (舍),
当n(n+1)=465时,解得:(舍),,
当n(n+1)=300时,解得:(舍),,
故选:B.
9.B
10.D
11.
12.
13.
14.
15.21
16.(1)每月盈利的平均增长率为20%;(2)按照这个平均增长率,预计今年五月份这家商店的盈利将达到10368元.
17.AB的长为8米.
18.(1)15,;(2)参加聚会的人数为9人;(3)线段数为
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
