24.1.2垂直于弦的直径练习题2021-2022学年人教版九年级数学上册(word版含简单答案)
文档属性
| 名称 | 24.1.2垂直于弦的直径练习题2021-2022学年人教版九年级数学上册(word版含简单答案) |  | |
| 格式 | docx | ||
| 文件大小 | 225.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 09:55:30 | ||
图片预览


文档简介
2021——2022学年度人教版九年级数学上册 第二十四章 圆 24.1.2 垂直于弦的直径 练习题
一、选择题
1.已知AB,CD是⊙O的两条平行弦,AB=8,CD=6,⊙O的半径为5,则弦AB与CD的距离为( )
A.1 B.7 C.4或3 D.7或1
2.如图,的直径为10,AB为弦,,垂足为C,若OC=4,则弦AB的长为( )
A.10 B.8 C.6 D.4
3.如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(﹣8,﹣4),则点N的坐标为( )
A.(-2,﹣4) B.(﹣1,﹣4) C.(﹣3,﹣4) D.(-1.5,﹣4)
4.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则△OFC的面积是( )
A.40cm2 B.20cm2 C.10cm2 D.5cm2
5.如图,⊙O的半径为5,C是弦AB的中点,OC=3,则AB的长是( )
A.6 B.8 C.10 D.12
6.如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为斜边向外作等腰直角三角形△ACD,△BCE,弧AC和弧BC的中点分别是M,N.连接DM,EN,若C在半圆上由点A向B移动的过程中,DM:EN的值的变化情况是( )
A.变大 B.变小
C.先变大再变小 D.保持不变
7.如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,AC=4,则OD的长为( )
A.1 B.1.5 C.2 D.2.5
8.如图,已知的直径弦于点则下列结论不一定成立的是( )
A. B. C. D.
9.如图,有一圆弧形桥拱,拱形半径,桥拱跨度,则拱高为( )
A. B. C. D.
10.如图,AB是⊙O的直径,C为⊙O上的点,把AOC沿OC对折,点A的对应点D恰好落在⊙O上,且C、D均在直径AB上方,连接AD、BD,若AC=4,BD=4,则AD的长度应是( )
A.12 B.10 C.8 D.6
二、填空题
11.在⊙O中,AB、CD是两条弦,AB=6,CD=8,且AB∥CD,⊙O的半径为5,则AB、CD之间的距离是____.
12.已知⊙O的半径为2,⊙O中有两条平行的弦AB和CD,AB=2,CD=2,则两条弦之间的距离为__.
13.已知半径为5的圆O中,弦AB=8,则以AB为底边的等腰三角形腰长为___________.
14.如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OEAC交半圆O于点E,过点E作EF⊥AB于F.若AC=4,则OF的长为_______.
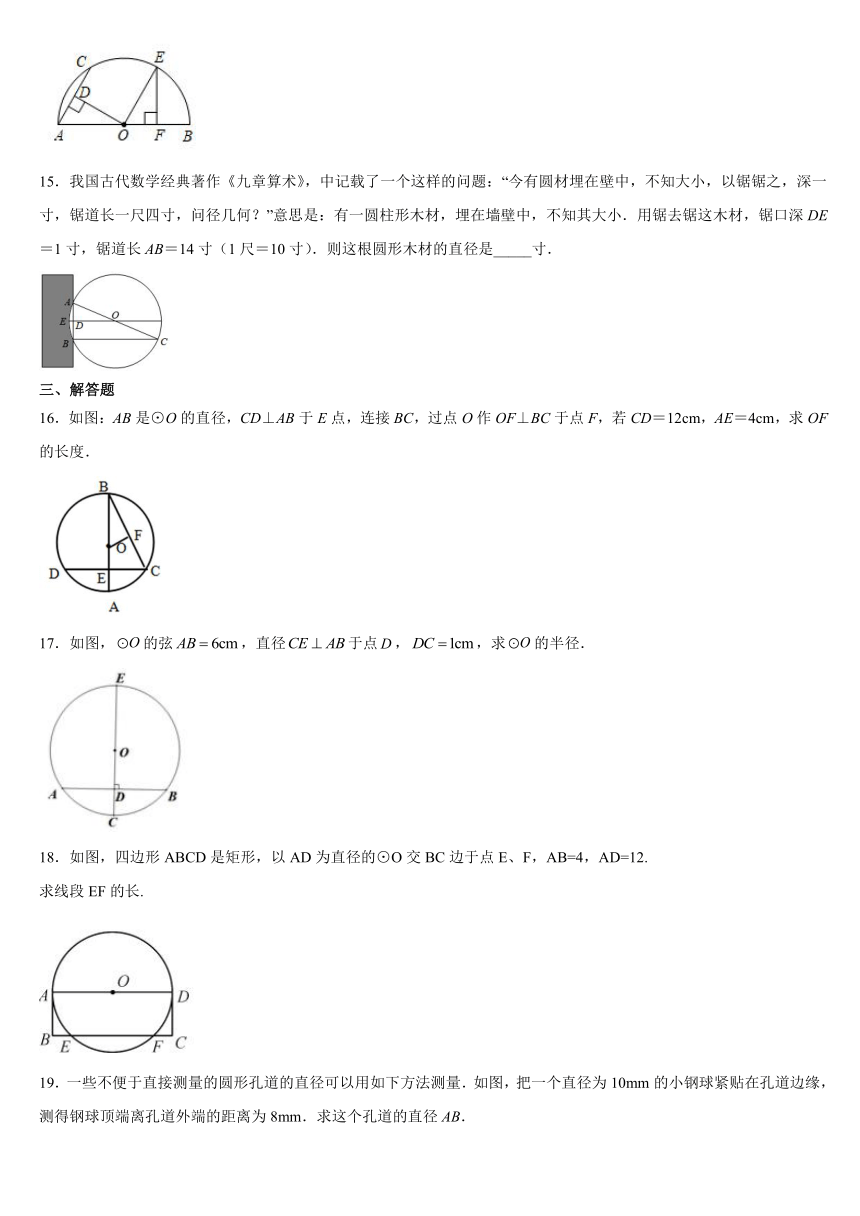
15.我国古代数学经典著作《九章算术》,中记载了一个这样的问题:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺四寸,问径几何?”意思是:有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深DE=1寸,锯道长AB=14寸(1尺=10寸).则这根圆形木材的直径是_____寸.
三、解答题
16.如图:AB是⊙O的直径,CD⊥AB于E点,连接BC,过点O作OF⊥BC于点F,若CD=12cm,AE=4cm,求OF的长度.
17.如图,的弦,直径于点,,求的半径.
18.如图,四边形ABCD是矩形,以AD为直径的⊙O交BC边于点E、F,AB=4,AD=12.
求线段EF的长.
19.一些不便于直接测量的圆形孔道的直径可以用如下方法测量.如图,把一个直径为10mm的小钢球紧贴在孔道边缘,测得钢球顶端离孔道外端的距离为8mm.求这个孔道的直径AB.
20.《九章算术》是我国古代著名数学经典,其中对勾股定理的论述比西方早一干多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小:以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锡口深1寸,锯道长1尺.如图,已知弦尺,弓形离寸,(注:1尺寸)问这块圆柱形木材的直径是多少寸?
21.如图,一拱形公路桥,圆弧形桥拱的水面跨度AB=80 m,桥拱到水面的最大高度为20 m.(1)求桥拱的半径.
(2)现有一艘宽60 m,顶部截面为长方形且高出水面9 m的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.
22.如图,已知正方形的边长为1,正方形中,点在的延长线上,点在上,点在线段上,且.以为半径的与直线交于点、.
(1)如图1,若点为中点,且点,点都在上,求正方形的边长.
(2)如图2,若点在上,求证:以线段和为邻边的矩形的面积为定值,并求出这个定值.
(3)如图3,若点在上,求证:.
23.(教材回顾)(1)如图①,点、分别是的边、边的中点,连结,则是的一条中位线.则和的数量关系是____,位置关系是_____.
(提出问题)如图④,是以为直径的⊙的一条弦,连结、,点在的上方,点在的下方,于,于,点、均在弦上.已知,,求的值.为了解决上面的问题,进行了如下的探究:
(分析问题)先看两种特殊情况:
(2)如图②,当点与点重合时,点也与点重合,点与点重合,此时,(点看成是长度为0的线段),则_____.(写出具体的数值)
(3)如图③,当时,、重合,此时与的数量关系是____,先根据条件易求的长度,则____.(写出具体的数值)
(解决问题)(4)结合图④对应的一般情况和你的感知,请用严谨的数学方法求的值.
【参考答案】
1.D 2.C 3.A 4.D 5.B 6.D 7.C 8.B 9.A 10.C
11.1
12.+1或-1
13.或
14.2
15.50
16.cm
17.5cm
18.4
19.直径为8mm.
20.26寸
21.(1) 桥拱的半径为50 m;(2)这艘轮船能顺利通过.
22.(1);(2);(3)略
23.(1);;(2);(3);;(4)
一、选择题
1.已知AB,CD是⊙O的两条平行弦,AB=8,CD=6,⊙O的半径为5,则弦AB与CD的距离为( )
A.1 B.7 C.4或3 D.7或1
2.如图,的直径为10,AB为弦,,垂足为C,若OC=4,则弦AB的长为( )
A.10 B.8 C.6 D.4
3.如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(﹣8,﹣4),则点N的坐标为( )
A.(-2,﹣4) B.(﹣1,﹣4) C.(﹣3,﹣4) D.(-1.5,﹣4)
4.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则△OFC的面积是( )
A.40cm2 B.20cm2 C.10cm2 D.5cm2
5.如图,⊙O的半径为5,C是弦AB的中点,OC=3,则AB的长是( )
A.6 B.8 C.10 D.12
6.如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为斜边向外作等腰直角三角形△ACD,△BCE,弧AC和弧BC的中点分别是M,N.连接DM,EN,若C在半圆上由点A向B移动的过程中,DM:EN的值的变化情况是( )
A.变大 B.变小
C.先变大再变小 D.保持不变
7.如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,AC=4,则OD的长为( )
A.1 B.1.5 C.2 D.2.5
8.如图,已知的直径弦于点则下列结论不一定成立的是( )
A. B. C. D.
9.如图,有一圆弧形桥拱,拱形半径,桥拱跨度,则拱高为( )
A. B. C. D.
10.如图,AB是⊙O的直径,C为⊙O上的点,把AOC沿OC对折,点A的对应点D恰好落在⊙O上,且C、D均在直径AB上方,连接AD、BD,若AC=4,BD=4,则AD的长度应是( )
A.12 B.10 C.8 D.6
二、填空题
11.在⊙O中,AB、CD是两条弦,AB=6,CD=8,且AB∥CD,⊙O的半径为5,则AB、CD之间的距离是____.
12.已知⊙O的半径为2,⊙O中有两条平行的弦AB和CD,AB=2,CD=2,则两条弦之间的距离为__.
13.已知半径为5的圆O中,弦AB=8,则以AB为底边的等腰三角形腰长为___________.
14.如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OEAC交半圆O于点E,过点E作EF⊥AB于F.若AC=4,则OF的长为_______.
15.我国古代数学经典著作《九章算术》,中记载了一个这样的问题:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺四寸,问径几何?”意思是:有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深DE=1寸,锯道长AB=14寸(1尺=10寸).则这根圆形木材的直径是_____寸.
三、解答题
16.如图:AB是⊙O的直径,CD⊥AB于E点,连接BC,过点O作OF⊥BC于点F,若CD=12cm,AE=4cm,求OF的长度.
17.如图,的弦,直径于点,,求的半径.
18.如图,四边形ABCD是矩形,以AD为直径的⊙O交BC边于点E、F,AB=4,AD=12.
求线段EF的长.
19.一些不便于直接测量的圆形孔道的直径可以用如下方法测量.如图,把一个直径为10mm的小钢球紧贴在孔道边缘,测得钢球顶端离孔道外端的距离为8mm.求这个孔道的直径AB.
20.《九章算术》是我国古代著名数学经典,其中对勾股定理的论述比西方早一干多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小:以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锡口深1寸,锯道长1尺.如图,已知弦尺,弓形离寸,(注:1尺寸)问这块圆柱形木材的直径是多少寸?
21.如图,一拱形公路桥,圆弧形桥拱的水面跨度AB=80 m,桥拱到水面的最大高度为20 m.(1)求桥拱的半径.
(2)现有一艘宽60 m,顶部截面为长方形且高出水面9 m的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.
22.如图,已知正方形的边长为1,正方形中,点在的延长线上,点在上,点在线段上,且.以为半径的与直线交于点、.
(1)如图1,若点为中点,且点,点都在上,求正方形的边长.
(2)如图2,若点在上,求证:以线段和为邻边的矩形的面积为定值,并求出这个定值.
(3)如图3,若点在上,求证:.
23.(教材回顾)(1)如图①,点、分别是的边、边的中点,连结,则是的一条中位线.则和的数量关系是____,位置关系是_____.
(提出问题)如图④,是以为直径的⊙的一条弦,连结、,点在的上方,点在的下方,于,于,点、均在弦上.已知,,求的值.为了解决上面的问题,进行了如下的探究:
(分析问题)先看两种特殊情况:
(2)如图②,当点与点重合时,点也与点重合,点与点重合,此时,(点看成是长度为0的线段),则_____.(写出具体的数值)
(3)如图③,当时,、重合,此时与的数量关系是____,先根据条件易求的长度,则____.(写出具体的数值)
(解决问题)(4)结合图④对应的一般情况和你的感知,请用严谨的数学方法求的值.
【参考答案】
1.D 2.C 3.A 4.D 5.B 6.D 7.C 8.B 9.A 10.C
11.1
12.+1或-1
13.或
14.2
15.50
16.cm
17.5cm
18.4
19.直径为8mm.
20.26寸
21.(1) 桥拱的半径为50 m;(2)这艘轮船能顺利通过.
22.(1);(2);(3)略
23.(1);;(2);(3);;(4)
同课章节目录
