2021—2022学年华东师大版九年级数学下册27.1.1 圆的基本元素 分层训练(Word版含答案)
文档属性
| 名称 | 2021—2022学年华东师大版九年级数学下册27.1.1 圆的基本元素 分层训练(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 190.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 00:00:00 | ||
图片预览


文档简介
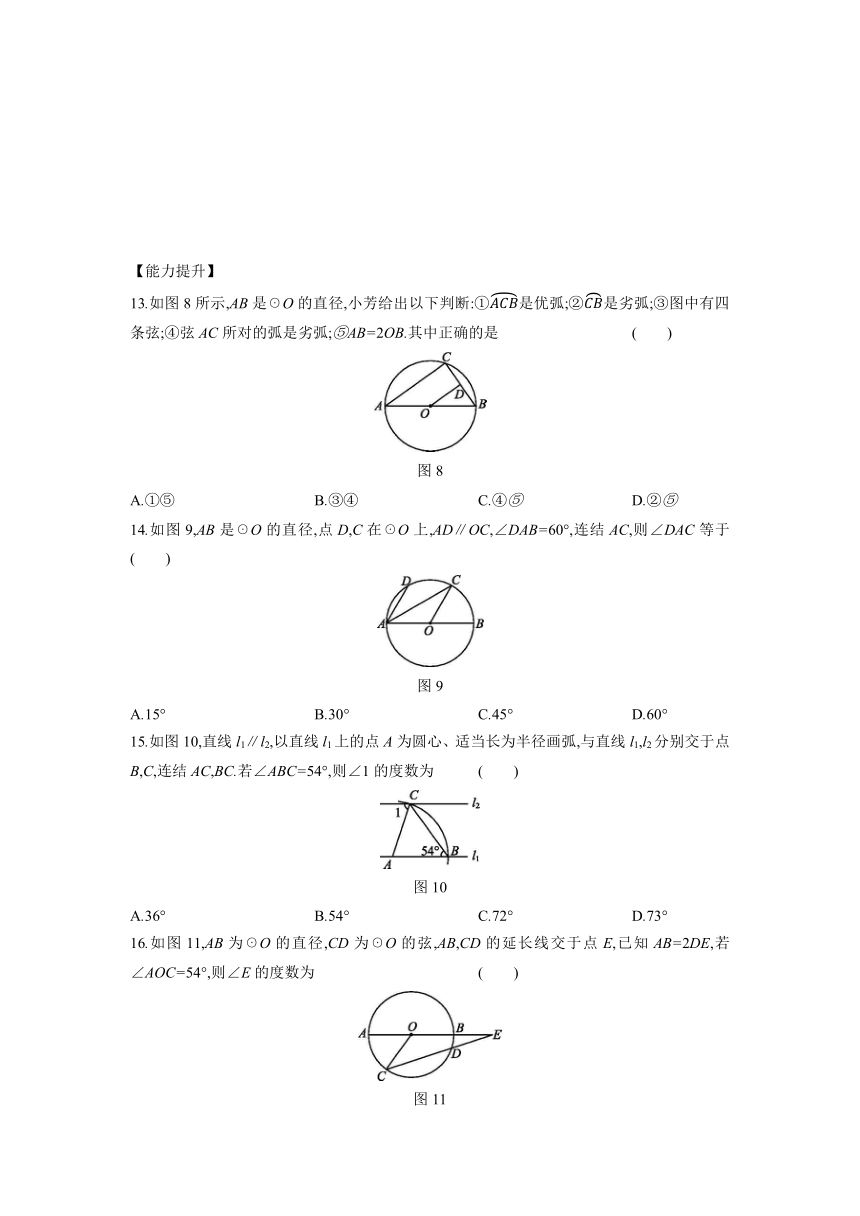
27.1.1 圆的基本元素
【基础练习】
知识点 1 圆的定义
1.下面关于圆的叙述正确的是 ( )
A.圆是一个面
B.圆是一条封闭的曲线
C.圆是由圆心唯一确定的
D.圆是到定点的距离等于或小于定长的点的集合
2.以已知点O为圆心,线段a的长为半径作圆,可以作 ( )
A.1个 B.2个 C.3个 D.无数个
3.确定一个圆的两个条件是 和 , 决定圆的位置, 决定圆的大小.
知识点 2 圆的基本元素
4.如图1,AB是圆O的直径,则圆中的弦有 条,分别是 ,劣弧有 条,分别是 .
图1
5.下列说法中,正确的是 ( )
A.过圆心的线段是直径
B.小于半圆的弧是优弧
C.弦是直径
D.半圆是弧
6.图2中的∠1是圆心角的是 ( )
图2
7.如图3所示,下列说法中正确的是( )
A.线段AB,AC,CD都是☉O的弦
B.线段AC经过圆心O,所以线段AC是直径
C.弦AC把☉O分成了两条不相等的弧
D.弦AB把圆分成两条弧,其中是劣弧 图3
知识点 3 与圆有关的简单计算与证明
8.如图4所示,MN为☉O的弦,∠M=40°,则∠N等于 ( )
图4
A.40° B.60° C.100° D.120°
9.圆内最长的弦的长为30 cm,则圆的半径是 .
10.如图5,☉O的半径为5,∠AOB=60°,则弦长AB= .
图5
11.如图6,在四边形ABCD中,∠DAB=∠DCB=90°,求证:A,B,C,D四个点在同一个圆上.
图6
12.如图7,A,B,C是☉O上的三点,BO平分∠ABC.求证:BA=BC.
图7
【能力提升】
13.如图8所示,AB是☉O的直径,小芳给出以下判断:①是优弧;②是劣弧;③图中有四条弦;④弦AC所对的弧是劣弧;⑤AB=2OB.其中正确的是 ( )
图8
A.①⑤ B.③④ C.④⑤ D.②⑤
14.如图9,AB是☉O的直径,点D,C在☉O上,AD∥OC,∠DAB=60°,连结AC,则∠DAC等于 ( )
图9
A.15° B.30° C.45° D.60°
15.如图10,直线l1∥l2,以直线l1上的点A为圆心、适当长为半径画弧,与直线l1,l2分别交于点B,C,连结AC,BC.若∠ABC=54°,则∠1的度数为 ( )
图10
A.36° B.54° C.72° D.73°
16.如图11,AB为☉O的直径,CD为☉O的弦,AB,CD的延长线交于点E,已知AB=2DE,若∠AOC=54°,则∠E的度数为 ( )
图11
A.27° B.24° C.20° D.18°
17.如图12,AB,CD是☉O的两条弦,若∠AOB+∠C=180°,∠COD=∠A,则∠AOB= °.
图12
18. 设AB=2 cm,作出满足下列要求的图形:
(1)到点A的距离等于1.5 cm,且到点B的距离等于1 cm的所有点组成的图形;
(2)到点A的距离小于1.5 cm,且到点B的距离小于1 cm的所有点组成的图形;
(3)到点A的距离大于1.5 cm,且到点B的距离小于1 cm的所有点组成的图形.
19.如图13,已知半径为5的☉O,A是☉O内的一点(点A与点O不重合),过点A且不过点O的直线与☉O交于B,C两点,连结OB,OC,过点A作OC的平行线交OB于点D.
(1)请正确画出示意图;
(2)求证:OD+DA为定值.
图13
27.1.1 圆的基本元素
1.B 2.A 3.圆心 半径的长度 圆心 半径的长度
4.2 CD,AB 5 ,,,, 5.D 6.D 7.B 8.A
9.15 cm 10.5
11.证明:如图,连结BD,取BD的中点O,连结OA,OC.
∵∠BAD=∠BCD=90°,OB=OD,
∴OA=OB=OD=OC,
∴A,B,C,D四个点在同一个圆上.
12.证明:如图,连结OA,OC.
∵OA=OB,OB=OC,
∴∠ABO=∠BAO,∠CBO=∠BCO.
∵BO平分∠ABC,
∴∠ABO=∠CBO,
∴∠BAO=∠BCO.
又∵BO=BO,
∴△OAB≌△OCB,
∴BA=BC.
D
14.B
15.C
16.D
17.108
18.解:(1)如图①,点P和点Q为所求.
(2)如图②,阴影部分为所求(不含边界).
(3)如图③,阴影部分为所求(不含边界).
19.解:(1)如图所示:
(2)证明:∵AD∥OC,
∴∠DAB=∠C.
又∵OB=OC,
∴∠B=∠C,
∴∠DAB=∠B,∴DB=DA,
∴OD+DA=OD+DB=OB,
即OD+DA为定值.
【基础练习】
知识点 1 圆的定义
1.下面关于圆的叙述正确的是 ( )
A.圆是一个面
B.圆是一条封闭的曲线
C.圆是由圆心唯一确定的
D.圆是到定点的距离等于或小于定长的点的集合
2.以已知点O为圆心,线段a的长为半径作圆,可以作 ( )
A.1个 B.2个 C.3个 D.无数个
3.确定一个圆的两个条件是 和 , 决定圆的位置, 决定圆的大小.
知识点 2 圆的基本元素
4.如图1,AB是圆O的直径,则圆中的弦有 条,分别是 ,劣弧有 条,分别是 .
图1
5.下列说法中,正确的是 ( )
A.过圆心的线段是直径
B.小于半圆的弧是优弧
C.弦是直径
D.半圆是弧
6.图2中的∠1是圆心角的是 ( )
图2
7.如图3所示,下列说法中正确的是( )
A.线段AB,AC,CD都是☉O的弦
B.线段AC经过圆心O,所以线段AC是直径
C.弦AC把☉O分成了两条不相等的弧
D.弦AB把圆分成两条弧,其中是劣弧 图3
知识点 3 与圆有关的简单计算与证明
8.如图4所示,MN为☉O的弦,∠M=40°,则∠N等于 ( )
图4
A.40° B.60° C.100° D.120°
9.圆内最长的弦的长为30 cm,则圆的半径是 .
10.如图5,☉O的半径为5,∠AOB=60°,则弦长AB= .
图5
11.如图6,在四边形ABCD中,∠DAB=∠DCB=90°,求证:A,B,C,D四个点在同一个圆上.
图6
12.如图7,A,B,C是☉O上的三点,BO平分∠ABC.求证:BA=BC.
图7
【能力提升】
13.如图8所示,AB是☉O的直径,小芳给出以下判断:①是优弧;②是劣弧;③图中有四条弦;④弦AC所对的弧是劣弧;⑤AB=2OB.其中正确的是 ( )
图8
A.①⑤ B.③④ C.④⑤ D.②⑤
14.如图9,AB是☉O的直径,点D,C在☉O上,AD∥OC,∠DAB=60°,连结AC,则∠DAC等于 ( )
图9
A.15° B.30° C.45° D.60°
15.如图10,直线l1∥l2,以直线l1上的点A为圆心、适当长为半径画弧,与直线l1,l2分别交于点B,C,连结AC,BC.若∠ABC=54°,则∠1的度数为 ( )
图10
A.36° B.54° C.72° D.73°
16.如图11,AB为☉O的直径,CD为☉O的弦,AB,CD的延长线交于点E,已知AB=2DE,若∠AOC=54°,则∠E的度数为 ( )
图11
A.27° B.24° C.20° D.18°
17.如图12,AB,CD是☉O的两条弦,若∠AOB+∠C=180°,∠COD=∠A,则∠AOB= °.
图12
18. 设AB=2 cm,作出满足下列要求的图形:
(1)到点A的距离等于1.5 cm,且到点B的距离等于1 cm的所有点组成的图形;
(2)到点A的距离小于1.5 cm,且到点B的距离小于1 cm的所有点组成的图形;
(3)到点A的距离大于1.5 cm,且到点B的距离小于1 cm的所有点组成的图形.
19.如图13,已知半径为5的☉O,A是☉O内的一点(点A与点O不重合),过点A且不过点O的直线与☉O交于B,C两点,连结OB,OC,过点A作OC的平行线交OB于点D.
(1)请正确画出示意图;
(2)求证:OD+DA为定值.
图13
27.1.1 圆的基本元素
1.B 2.A 3.圆心 半径的长度 圆心 半径的长度
4.2 CD,AB 5 ,,,, 5.D 6.D 7.B 8.A
9.15 cm 10.5
11.证明:如图,连结BD,取BD的中点O,连结OA,OC.
∵∠BAD=∠BCD=90°,OB=OD,
∴OA=OB=OD=OC,
∴A,B,C,D四个点在同一个圆上.
12.证明:如图,连结OA,OC.
∵OA=OB,OB=OC,
∴∠ABO=∠BAO,∠CBO=∠BCO.
∵BO平分∠ABC,
∴∠ABO=∠CBO,
∴∠BAO=∠BCO.
又∵BO=BO,
∴△OAB≌△OCB,
∴BA=BC.
D
14.B
15.C
16.D
17.108
18.解:(1)如图①,点P和点Q为所求.
(2)如图②,阴影部分为所求(不含边界).
(3)如图③,阴影部分为所求(不含边界).
19.解:(1)如图所示:
(2)证明:∵AD∥OC,
∴∠DAB=∠C.
又∵OB=OC,
∴∠B=∠C,
∴∠DAB=∠B,∴DB=DA,
∴OD+DA=OD+DB=OB,
即OD+DA为定值.
